Разбираем EM-algorithm на маленькие кирпичики14.05.2020 12:38

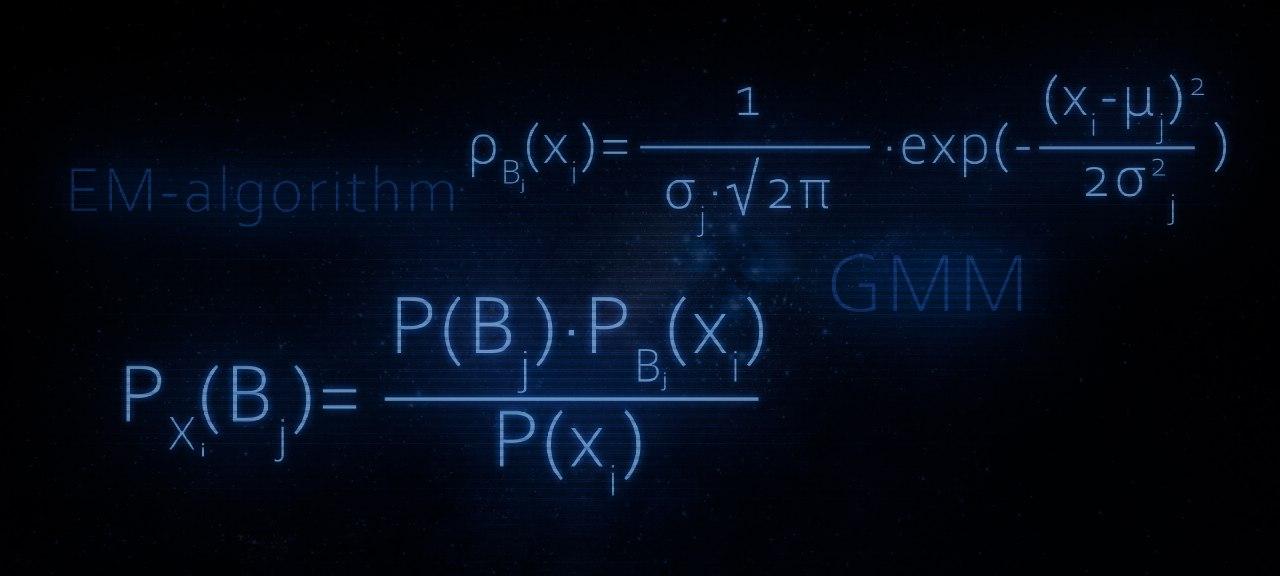
hpmvngrdxhgiu_a7b9vjyx4shsm.jpeg

В этой статье, как Вы уже, наверное догадались, речь пойдет об устройстве EM-алгоритма. Статья прежде всего может быть интересна тем, кто потихонечку уже вступает в сообщество датасайнтистов. Материал изложенный в статье в большей степени будет полезен тем, кто недавно начал проходить третий курс «Поиск структуры в данных» в рамках специализации «Машинное обучение и анализ данных» от МФТИ и Яндекс.

Изложенный в статье материал, в каком-то смысле, является дополнением к первой неделе обучения на вышеобозначенном курсе, а именно, позволяет ответить на некоторые немаловажные вопросы, касательно принципа действия EM-алгоритма. Для лучшего понимания материала нашему многоуважаемому читателю желательно уметь осуществлять операции с матрицами (умножение матриц, нахождение определителя матрицы и обратной матрицы), разбираться в основах теории вероятности и матстата, ну и конечно же, иметь хотя бы базовое представление о базовых алгоритмах кластеризации и понимать какое место кластеризация занимает в машинном обучении. Хотя, безусловно, и без этих знаний можно ознакомиться со статьей, что-то да наверняка будет понятным :)

Также по старой традиции, статья не будет содержать глубоких теоретических изысканий, но будет наполнена простыми и доступными для понимания примерами. Каждый последующий пример будет немного глубже предыдущего объяснять действие EM-алгоритма, что в конечном итоге приведет нас прямёхонько к разбору самого алгоритма. Для каждого примера будет написан код. Весь код написан на языке python 2.7, и за это я заранее приношу извинения. Так вышло, что сейчас я использую именно эту версию, но после перехода на python 3, постараюсь изменить код в статье.

Ознакомимся с планом статьи:

1) Рассмотрим в общих чертах как устроен EM-алгоритм.

2) Повторим основные моменты из теоремы (формулы) Байеса:

$P_{x_i}(B_j) = \frac{P(B_j) \centerdot P_{B_j}(x_i)}{P(x_i)} $

3) Рассмотрим первый пример на теорему Байеса, в котором все элементы формулы (а точнее вероятности $P(B_j), P_{B_j}(x_i)$) за знаком равенства справа известны. В этом случае нам требуется только правильно понять какие цифры куда подставить и далее выполнить элементарные операции.

4) Рассмотрим второй пример на теорему Байеса. Для решения задачи нам необходимо будет уже дополнительно вычислить плотность вероятности определенного события ($x_i$) при условии гипотезы ($B_j$) — $\rho_{B_j}(x_i)$. Для вычислений нам будут даны параметры случайной величины, а именно, математическое ожидание — $\mu$ и стандартное отклонение — $\sigma$. Вычисления плотности вероятности будут осуществляться по следующей формуле:

$\rho_{B_j}(x_i) = \frac{1}{\sigma_j \centerdot \sqrt{2 \pi}} \centerdot \exp(- \frac{(x_i-\mu_j)^2}{2 \sigma_j^2}) $


Использование вышеобозначенной формулы предполагает, что случайная величина имеет одномерное измерение и распределена нормально (иначе говорят — распределение Гаусса или Гаусса-Лапласа распределение вероятностей).

5) Рассмотрим третий пример, который отличается от предыдущего только тем, что в нем рассматривается случай многомерного (в нашем варианте двумерного) нормального распределения случайной величины. В таком случае вычисление плотностей осуществляется по следующей формуле:

$\rho_{B_j}(x_i) = \frac{1}{(2\pi)^{k/2} \centerdot \mid \Sigma_j\mid ^{1/2}} \centerdot \exp(- \frac{1}{2} \centerdot (x_i-\mu_j)^T \Sigma_j^{-1} (x_i-\mu_j))$

6) И наконец, мы модифицируем третий пример таким образом, чтобы наглядно продемонстрировать работу EM-алгоритма.

7) В завершении, сравним качество работы выведенного нами алгоритма с качеством работы EM-алгоритма, который встроен в библиотеку sklearn (class sklearn.mixture.GaussianMixture)

Если Вы вместо формул, указанных в плане статьи, увидели японские иероглифы, то пожалуйста не пугайтесь — после теоремы Байеса (второго пункта плана статьи), мы будем разбирать такие примеры, которые Вы наверняка будете понимать, как минимум, на интуитивном уровне. Ну что же, погнали!

EM-алгоритм в общих чертах


На курсе, по мотивам, которого написана статья, EM-алгоритм приводится в качестве одного из способов кластеризации. Другими словами, это метод машинного обучения без учителя, когда нам заранее не известны истинные ответы. В нашей статье, мы также будем рассматривать алгоритм в рамках одного из метода кластеризации случайной величины, имеющей нормальное распределение. Однако следует отметить, что алгоритм имеет более широкое применение. EM-алгоритм (англ. expectation-maximization) — это общий метод нахождения оценок функции правдоподобия в моделях со скрытыми переменными, который из смеси распределений позволяет строить (приближать) сложные вероятностные распределения.

EM-алгоритм в задачах кластеризации используется как итеративный алгоритм, который на каждой итерации осуществляет два шага:

E-шаг. На первом E-шаге мы каким-либо образом, например, случайным, выбираем скрытые переменные, в нашем случае это будут математическое ожидание — $\mu$ и стандартное отклонение — $\sigma$. Используя выбранные переменные, рассчитываем вероятность отнесения каждого объекта к тому или иному кластеру. При последующих E-шагах используются скрытые переменные, определенные на M-шагах.

M-шаг. На M-шаге мы, в соответствии с полученными на E-шаге значениями вероятностей отнесения каждого объекта к тому или иному кластеру, пересчитываем скрытые переменные $\mu$ и $\sigma$

Итерации повторяются до тех пор, пока не наступит сходимость. Можно считать, что сходимость наступила тогда, когда значения скрытых переменных изменяются не значительно, например, в пределах заданной константы. В последнем примере, который рассматривается в статье мы не будем задавать константы и соответственно не будем определять изменения значений скрытых переменных на каждой итерации. Поступим проще — ограничим наш алгоритм фиксированным количеством шагов.

M-шаг достаточно прост для понимания и в этом мы убедимся на последнем примере. Основное внимание в статье мы уделим E-шагу.

В основе E-шага лежит теорема Байеса, на основании которой мы и определяем вероятность каждого объекта на отнесение к тому или иному кластеру. Давайте вспомним, о чем эта теорема.

Вспомним формулу Байеса

$P_{x_i}(B_j) = \frac{P(B_j) \centerdot P_{B_j}(x_i)}{P(x_i)} $

, где $P_{x_i}(B_j)$ — вероятность того, что при наступившем событии $x_i$ имела место гипотеза $B_j$

$P(B_j)$ — вероятность наступления гипотезы $B_j$

$P_{B_j}(x_i)$ — вероятность наступления события $x_i$ при условии гипотезы $B_j$

$P(x_i)$ — вероятность наступления события $x_i$ при условии выполнения каждой гипотезы (рассчитывается по формуле полной вероятности события)

При условии, что событие $x_i$ уже произошло, вероятность выполнения гипотезы $B_j$ переоценивается по вышеуказанной формуле. Можно сказать так, что $P(B_j)$ это априорная вероятность выполнения гипотезы (до испытания), а $P_{x_i}(B_j)$ — это апостериорная вероятность той же гипотезы, оцененной после наступления события $x_i$, то есть с учетом того, что событие $x_i$ достоверно произошло.

Пример первый на теорему Байеса

Представим, что нам на склад поступили детали, которые были произведены на двух разных станках. Известны следующие характеристики поступивших на склад изделий:

Всего на склад поступило деталей — 10000 шт ($N = 10000$), из них деталей, произведенных на первом станке — 6000 шт. ($N1 = 6000$), на втором — 4000 шт. ($N2 = 4000$).

Доля стандартных (т.е. не бракованных) изделий, произведенных на первом станке, составляет 0.9, доля стандартных изделий, произведенных на втором станке составляет 0.8.

Мы случайным образом извлекли из поступивших деталей одну деталь, и она оказалась стандартной.

Нам требуется определить вероятность того, что:

1) деталь произведена на 1-м станке;

2) деталь произведена на 2-м станке.

Решение

1) Событием $x$ в нашем примере является извлечение стандартного изделия.

2) Теперь, определимся с гипотезами $B_j$. У нас две партии деталей, а значит две гипотезы:

Гипотеза $B_1$: случайно извлеченное изделие произведено на станке №1.

Гипотеза $B_2$: случайно извлеченное изделие произведено на станке №2.

Соответственно, вероятность извлечь изделие, произведенное на первом станке — $P(B_1)$ составляет $N1/N = 6000/10000 = 0.6$.

Вероятность извлечь изделие, произведенное на втором станке — $P(B_2)$ составляет $N2/N = 0.4$. Причем нам не важно стандартное изделие или бракованное, важно из какой оно партии.

3) Вероятность извлечь стандартное изделие из изделий, произведенных на станке №1 (то есть, при условии первой гипотезы) соответствует доли стандартных изделий, произведённых на станке №1 и составляет 0.9, $P_{B_1}(x_i) = 0.9$.

Вероятность извлечь изделие стандартное изделие при условии гипотезы №2 — $P_{B_2}(x_i) = 0.8$

4) Определим вероятность извлечь стандартное изделие из всей совокупности изделий — $P(x_i)$. В соответствии с формулой полной вероятности события $P(x_i) = P(B_1) \centerdot P_{B_1}(x_i) + P(B_2) \centerdot P_{B_2}(x_i) = 0.6 \centerdot 0.9 + 0.4 \centerdot 0.8 = 0.54 + 0.32 = 0.86$. Здесь мы понимаем, что тогда $0.14$ — это вероятность извлечь бракованную деталь из всех поступивших на склад деталей и в сумме получается 1 $(0.86 + 0.14 = 1)$.

5) Теперь у нас есть все данные для того, чтобы решить задачу.

5.1) Определим вероятность того, что случайным образом извлеченная стандартная деталь, произведена на станке $№1$:

$P_{x_i}(B_1) = \frac{P(B_1) \centerdot P_{B_1}(x_i)}{P(x_i)} = \frac{0.6 \centerdot 0.9}{0.86} \approx 0.63$

5.2) Определим вероятность того, что случайным образом извлеченная стандартная деталь, произведена на станке $№2$:

$P_{x_i}(B_2) = \frac{P(B_2) \centerdot P_{B_2}(x_i)}{P(x_i)} = \frac{0.4 \centerdot 0.8}{0.86} \approx 0.37$

Таким образом, мы провели переоценку гипотез $B_1$ и $B_2$. После переоценки, гипотезы также образуют полную группу событий: $0.63 + 0.37 = 1$.

Ну что же, теперь самое время перейти ко второму примеру.

Второй пример на теорему Байеса с использованием параметров нормального распределения случайной величины: математического ожидания $\mu$ и стандартного отклонения $\sigma$

Давайте слегка модифицируем условия предыдущего примера. Будем считать, что нам не известны доли стандартных изделий, производимых на станках №1 и №2, но допустим, вместо этого мы знаем средние размеры диаметров изделий и стандартное отклонение диаметра изделий на каждом станке.

Станок №1 производит детали размером 64 мм в диаметре и стандартным отклонением 4 мм.

Станок №2 производит детали размером 52 мм в диаметре и стандартным отклонением в 2 мм.

Немаловажное условие — вся совокупность изделий описывается нормальным распределением или распределением Гаусса.

В остальном условия те же, запишем их:

$N1 = 6000, \mu_1 = 64, \sigma_1 = 4$

$N2 = 4000, \mu_2 = 52, \sigma_2 = 2$

Будем считать, что в процессе приемки продукции произошел небольшой инцидент, в результате которого все изделия перемешались.

Наша задача перебрать детали и для каждой определить вероятность того, что она была произведена на станке №1 или на станке №2. Также мы будем считать, что деталь произведена на том станке, вероятность которого выше.

Решение

В первую очередь, разберем алгоритм решения. Мы легко можем посчитать вероятность каждой гипотезы, впрочем мы уже знаем их значения из прошлого примера: $P(B_1)=0.6$, $P(B_2)=0.4$. Но как нам посчитать вероятность изъять стандартное изделие по отдельности для каждой из имеющихся гипотез? Все просто! Мы и не будем считать вероятность, вместо этого мы определим плотность вероятности изъять деталь с ее значением диаметра для каждой гипотезы в отдельности.

Для этого воспользуемся общеизвестной формулой:

$\rho_{B_j}(x_i) = \frac{1}{\sigma_j \centerdot \sqrt{2 \pi}} \centerdot \exp(- \frac{(x_i-\mu_j)^2}{2 \sigma_j^2}) $

, где $x_i$ — случайная величина (в нашем случае фактический размер диаметра изделия),

$\mu_j$ — математическое ожидание случайных величин $j$-ой гипотезы (в нашем случае — средний размер диаметра изделия, произведенного на $j$-м станке),

$\sigma_j $ — стандартное отклонение случайных величин $j$-ой гипотезы (в нашем случае — отклонение от среднего размера диаметра изделия, произведенного на $j$-м станке).

Таким образом, мы делаем ловкую замену вероятности на плотность вероятности в числителе формулы Байеса, аналогичные замены проведем в знаменателе.

Адаптируем формулы конкретно для нашего случая.

Вероятность того, что деталь с размерами диаметра $x_i$ произведена на станке №1 определим по формуле:

$P_{x_i}(B_1) = \frac{w_1 \centerdot \rho_{B_1}(x_i)}{w_1 \centerdot \rho_{B_1}(x_i) + w_2 \centerdot \rho_{B_1}(x_i)}$

Вероятность того, что деталь с размерами диаметра $x_i$ произведена на станке №2:

$P_{x_i}(B_2) = \frac{w_2 \centerdot \rho_{B_2}(x_i)}{w_1 \centerdot \rho_{B_1}(x_i) + w_2 \centerdot \rho_{B_1}(x_i)}$

Заметим, что мы заменили обозначение вероятности гипотезы с $P(B_j)$ на $w_j$. Это связано с соответствующим обозначением на ранее обозначенном курсе. Далее мы будем использовать именно такое обозначение.

Теперь мы укомплектованы на все 100% и готовы к решению задачи.

Смотрим код

Импорт библиотек 
# импортируем библиотеки, модули
import numpy as np
import random
import math
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.metrics import accuracy_score


Функции, используемые во втором примере 
# функция определения плотности вероятности извлечь деталь, произведенную заданном на станке
# то есть мы задаем параметры станка: мат.ожидание, среднее кв. отклонение
def gaus_func_01(mu,sigma,x):
    return math.e**(-(x-mu)**2/(2*sigma**2)) / (sigma*(2*math.pi)**0.5)

# напишем функцию определения вероятностей принадлежности деталей к станку
def proba_x(X, w1, w2, mu_1, mu_2, sigma_1, sigma_2):
    for i in X:
        P1_x = gaus_func_01(mu_1,sigma_1,i)
        P2_x = gaus_func_01(mu_2,sigma_2,i)
        P_x = w1*P1_x + w2*P2_x
        P_x_1 = (w1*P1_x)/P_x
        P_x_2 = (w2*P2_x)/P_x
        proba_temp = []
        proba_temp.append(P_x_1)
        proba_temp.append(P_x_2)
        proba_X.append(proba_temp)
    return proba_X

# напишем функцию отнесения изделия к тому или станку
def pred_x(proba_X, limit_proba):
    pred_X = []
    for x in proba_X:
        if x[0] >= limit_proba:
            pred_X.append(1)
        else:
            pred_X.append(2)
    return np.array(pred_X)

# напишем функцию построения графиков
def graph_01(X, pred_X, mu_1, sigma_1, mu_2, sigma_2):
    true_pred = []
    false_pred_1 = []
    false_pred_2 = []
    for i in range(X.shape[0]):
        if pred_X[i] == y[i]:
            true_pred.append([X[i], -0.025])
        else:
            if y[i] == 1:
                false_pred_1.append([X[i], -0.0075])
            else:
                false_pred_2.append([X[i], -0.015])

    false_pred_1 = np.array(false_pred_1)            
    false_pred_2 = np.array(false_pred_2)
    true_pred = np.array(true_pred)

    x_theory = np.linspace(42, 85, 20000)
    y_theory_1 = []
    for x in x_theory:
        y_theory_1.append(gaus_func_01(mu_1,sigma_1,x))
    y_theory_2 = []
    for x in x_theory:
        y_theory_2.append(gaus_func_01(mu_2,sigma_2,x))

    plt.figure(figsize=(18, 8))    
    plt.plot(
        x_theory, y_theory_1, color = 'green', lw = 2, label = 'Theoretical probability density for machine 1')
    plt.plot(
        x_theory, y_theory_2, color = 'firebrick', lw = 2, label = 'Theoretical probability density for machine 2')
    plt.hist(
        X[:N1], bins = 'auto', color='#539caf', normed = True, alpha = 0.35, label = 'machine tool products 1')
    plt.hist(
        X[N1:N], bins = 'auto', color='sandybrown', normed = True, alpha = 0.75, label = 'machine tool products 2')
    plt.plot(mu_1, 0, 'o', markersize = 11, color = 'blue', label = 'Mu 1')
    plt.plot(mu_2, 0, 'o', markersize = 11, color = 'red', label = 'Mu 2')

    plt.plot([mu_1 - sigma_1, mu_1 - sigma_1], [0,0.85*np.max(y_theory_1)],
             ':', lw = 3, color = 'blue', alpha = 0.55, label = 'Mu1 - sigma1')
    plt.plot([mu_1 + sigma_1, mu_1 + sigma_1], [0,0.85*np.max(y_theory_1)],
             ':', lw = 3, color = 'blue', alpha = 0.55, label = 'Mu1 + sigma1')
    plt.plot([mu_2 - sigma_2, mu_2 - sigma_2], [0,0.85*np.max(y_theory_2)],
             ':', lw = 3, color = 'red', alpha = 0.55, label = 'Mu2 - sigma2')
    plt.plot([mu_2 + sigma_2, mu_2 + sigma_2], [0,0.85*np.max(y_theory_2)],
             ':', lw = 3, color = 'red', alpha = 0.55, label = 'Mu2 + sigma2')

    plt.plot([mu_1 - 2 * sigma_1, mu_1 - 2 * sigma_1], [0, 0.9*0.5 * np.max(y_theory_1)],
             ':', lw = 2.5, color = 'blue', alpha = 0.35, label = 'Mu1 - 2*sigma1')
    plt.plot([mu_1 + 2 * sigma_1, mu_1 + 2 * sigma_1], [0, 0.9*0.5 * np.max(y_theory_1)],
             ':', lw = 2.5, color = 'blue', alpha = 0.35, label = 'Mu1 + 2*sigma1')
    plt.plot([mu_2 - 2 * sigma_2, mu_2 - 2 * sigma_2], [0, 0.9*0.5 * np.max(y_theory_2)],
             ':', lw = 2.5, color = 'red', alpha = 0.35, label = 'Mu2 - 2*sigma2')
    plt.plot([mu_2 + 2 * sigma_2, mu_2 + 2 * sigma_2], [0, 0.9*0.5 * np.max(y_theory_2)],
             ':', lw = 2.5, color = 'red', alpha = 0.35, label = 'Mu2 + 2*sigma2')

    plt.plot(false_pred_1[:,0], false_pred_1[:,1], 'o', markersize = 2.5, color = 'blue', alpha = 0.2, label = 'errors1')
    plt.plot(false_pred_2[:,0], false_pred_2[:,1], 'o', markersize = 2.5, color = 'red', alpha = 0.3, label = 'errors2')
    plt.plot(true_pred[:,0], true_pred[:,1], 'o', markersize = 3, color = 'green', alpha = 0.2, label = 'right answers')

    plt.xlabel('Caliber')
    plt.ylabel('Probability density')
    plt.legend()
    plt.show()


Укажем параметры 
# сформируем начальные условия примера
# количество изделий произведенных на станке №1
N1 = 6000
# количество изделий произведенных на станке №2
N2 = 4000
# количество изделий произведенных на обоих станках
N = N1+N2

# диаметр изделия станка №1
mu_1 = 64.
# стандартное отклонение в размере диаметра изделий станка №1
sigma_1 = 3.5

# диаметр изделия станка №2
mu_2 = 52
# стандартное отклонение в размере диаметра изделий станка №2
sigma_2 = 2.


Проведем расчет 
X = np.zeros((N))
np.random.seed(seed=42)
# инициализируем данные по деталям, производства станка №1
X[:N1] = np.random.normal(loc=mu_1, scale=sigma_1, size=N1)
# инициализируем детали, производства станка №2
X[N1:N] = np.random.normal(loc=mu_2, scale=sigma_2, size=N2)

# инициализируем вектор ответов
y = np.zeros((N))
y[:N1] = np.array((1))
y[N1:N] = np.array((2))

# определим априорную вероятность извлечь изделие, произведенное на станке №1
w1 = float(N1)/N
# определим априорную вероятность извлечь изделие, произведенное на станке №2
w2 = float(N2)/N

# для каждой детали определим вероятность принадлежности к тому или иному станку
proba_X = []
proba_X = proba_x(X, w1, w2, mu_1, mu_2, sigma_1, sigma_2)

# установим порог вероятности, при достижении которого, изделие будет относиться к тому или иному станку
limit_proba = 0.5

# определим принадлежность детали к станку
pred_X = []
pred_X = pred_x(proba_X, limit_proba)

# определим качество нашего алгоритма
print 'Доля верно определенных изделий:', round(accuracy_score(y, pred_X),3)
print

print 'График №1'
graph_01(X, pred_X, mu_1, sigma_1, mu_2, sigma_2)

График №1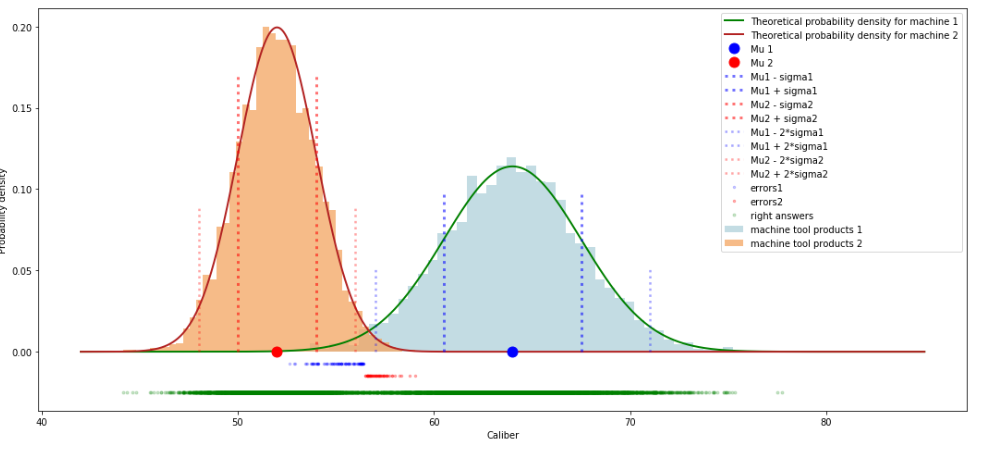
i_ibrlvpaxrtmpgyozwzosdmadi.png

Что мы только что сделали? Мы сгенерировали псевдослучайным образом 10000 значений, описываемых нормальным распределением, из них 6000 значений с математическим ожиданием в 64 мм и стандартным отклонением 4 мм, 4000 значений с математическим ожиданием равным 52 мм и стандартным отклонением в 2 мм. Далее, в соответствии с вышеуказанным алгоритмом, для каждой детали определили вероятность ее производства на станке №1 или №2. После этого выбрали гипотезу о производстве изделия на том или ином станке в зависимости от того, какая гипотеза имеет большую вероятность. И наконец сравнили результаты нашего алгоритма с истинными ответами.

На выходе мы получили долю правильных ответов — 0.986. В целом это очень неплохо, учитывая, что обучение мы проводили без использования истинных ответов.

Посмотрим на график. На что рекомендуется обратить внимание? Посмотрите, где расположены не верно определенные алгоритмом изделия.

Во-первых, мы видим ошибки алгоритма только в той области, где изделия, произведенные на разных станках, имеют один и тот же диаметр. Это выглядит вполне логичным.

Во-вторых, мы видим, что алгоритм ошибается только в тех объектах, которые больше всего удалены от истинного среднего значения объектов и при этом находятся достаточно близко к ложному центру.

Но самое интересное в том, что проблемы начинаются в основном, после пересечения значений приблизительно равных $\mu +- 2\sigma$, конкретно в нашем случае на пересечении $\mu_1 - 2\sigma_1$ и $\mu_2 + 2\sigma_2$

Желающие могут «покрутить» параметры и посмотреть как меняется качество алгоритма. Это будет полезно для лучшего усвоения материала.

Ну, а мы двигаемся дальше к следующему примеру

Третий пример. Двумерный случай.

В этот раз мы рассмотрим случай, когда у нас есть данные не только о диаметре изделий, но и о, например, весе каждого изделия. Пускай станок №1 производит детали весом в 12 г. и стандартным отклонением в 1 г., станок №2 производит изделия весом в 10 г. и стандартным отклонением 0.8 мм

В остальном будем использовать данные из предыдущего примера, запишем их.

$N1 = 6000, \mu_{1 1} = 64, \sigma_{1 1} = 4, \mu_{1 2} = 14, \sigma_{1 2} = 1$

$N2 = 4000, \mu_{2 1} = 52, \sigma_{2 1} = 2, \mu_{2 2} = 10, \sigma_{2 2} = 0.9$

Ситуация та же — все детали перемешались в одну большую кучу и нам нужно их перебрать и определить для каждой детали вероятность ее производства на станке №1 и станке №2.

Решение

В целом подход решения относительно предыдущего примера не меняется за исключением формулы определения плотности вероятности случайной величины. Для многомерного случая используется следующая формула:

$p_{B_j}(x_i) = \frac{1}{(2\pi)^{k/2} \centerdot \mid \Sigma_j\mid ^{1/2}} \centerdot \exp(- \frac{1}{2} \centerdot (x_i-\mu_j)^T \Sigma_j^{-1} (x_i-\mu_j))$

, где $\Sigma_j$ — это матрица ковариаций cлучайных величин $j$-й гипотезы (в нашем случае, матрица ковариаций параметров изделий, произведенных на $j$-м станке)

$\mid \Sigma_j\mid$ — это определитель матрицы ковариации случайных величин $j$-й гипотезы

$\mu_j$ — математическое ожидание случайных величин $j$-ой гипотезы (в нашем случае, среднее значение изделий, произведенных на $j$-м станке)

$x_i$ — случайная величина (в нашем случае параметры $i$-го изделия)

В этот раз, для понимания кода, уважаемому читателю понадобятся знания об операциях с матрицами

Функции, используемые в третьем примере 
# функция определения плотности вероятности извлечь деталь, произведенную заданном на станке
# то есть мы задаем параметры станка: мат.ожидание, среднее кв. отклонение
def gaus_func_02(k, m, x, mu, sigma):
    pj_xi = []
    for j in range(k):
        det_sigma_j = np.linalg.det(sigma[j])
        factor_1 = 1 / (((2 * math.pi)**(k/2)) * ((det_sigma_j)**0.5))
        factor_2 = []
        for i in x:
# обратим внимание на то, что запись в коде отличается от записи показателя экспоненты в обшепринятой функции
# в общепринятом виде первым множетелем идет транспонированная матрица центрированных значений
# у нас наоборот. Это связано с тем, что мы изначально использовали иной формат
# спишем это на технические обстоятельства
            factor_2.append(math.e**float(
            -0.5 * np.matrix(i - mu[j]) * np.matrix(np.linalg.inv(sigma[j])) * np.matrix(i - mu[j]).T))
        pj_xi.append(factor_1 * np.array(factor_2))
    return np.array(pj_xi)

# напишем функцию определения вероятности того, что извлеченный объект относится к кластеру №1 и №2
def proba_func_02(pjxi, w, k):
    # для начала определим вероятность извлечь объект из всей совокупности данных
    P_X = []
    for j in range(k):
        P_X.append(w[j] * pjxi[j])
    P_X = np.sum(np.array(P_X), axis = 0)
    # теперь определим вероятность того, что извлеченный объект относится к кластеру №1 и №2
    P_J_X = []
    for j in range(k):
        P_J_X.append(w[j] * pjxi[j] / P_X)
    return np.array(P_J_X)

# напишем функцию отнесения изделия к тому или станку
def pred_x_02(proba_X, limit_proba):
    pred_X = []
    for x in proba_X[0]:
        if x >= limit_proba:
            pred_X.append(1)
        else:
            pred_X.append(2)
    return np.array(pred_X)

# напишем функцию построения графика с распределением изделий по станкам в соответствии с алгоритмом
def graph_02_algorithm(pred_X, mu):
    # преобразуем массив данных
    pred_X = np.array(pred_X)

    # запишем параметры изделий, в раздельные массивы в соответствии с определением станка алгоритмом
    answers_1 = []
    answers_2 = []

    for i in range(pred_X.shape[0]):
        if pred_X[i] == 1:
            answers_1.append(X[i])
        else:
            answers_2.append(X[i])
    
    print 'График "Распределение изделий в соответствии с алгоритмом"'
    plt.figure(figsize=(16, 6))  
    plt.plot(
        np.array(answers_1)[:,0], np.array(answers_1)[:,1], 'o', alpha = 0.7, color='sandybrown', label = 'Produced on machine #1')
    plt.plot(
        np.array(answers_2)[:,0], np.array(answers_2)[:,1], 'o', alpha = 0.45, color = 'darkblue', label = 'Produced on machine #2')
    plt.plot(mu[0][0], mu[0][1], 'o', markersize = 16, color = 'red', label = 'Mu 1')
    plt.plot(mu[1][0], mu[1][1], 'o',  markersize = 16, color = 'slateblue', label = 'Mu 2')
    plt.xlabel('Diameter')
    plt.ylabel('Weight')
    plt.legend()
    plt.show()
    
# напишем функцию построения графика с истинным распределением изделий по станкам
def graph_02_true(X, mu):
    print 'График "Истинное распределение изделий"'
    plt.figure(figsize=(16, 6))  
    plt.plot(
        X[0:N1,0], X[0:N1,1], 'o', alpha = 0.7, color='sandybrown', label = 'Produced on machine #1')
    plt.plot(
        X[N1:N,0], X[N1:N,1], 'o', alpha = 0.45, color = 'darkblue', label = 'Produced on machine #2')
    plt.plot(mu[0][0], mu[0][1], 'o', markersize = 16, color = 'red', label = 'Mu 1')
    plt.plot(mu[1][0], mu[1][1], 'o',  markersize = 16, color = 'slateblue', label = 'Mu 2')
    plt.xlabel('Diameter')
    plt.ylabel('Weight')
    plt.legend()
    plt.show()


Укажем параметры 
# количество станков
k = 2

# количество деталей изготовленных на станке №1
N1 = 6000
# количество деталей изготовленных на станке №2
N2 = 4000
N = N1+N2

# количество признаков (диаметр и вес)
m = 2

# диаметр изделия станка №1
mu_1_1 = 64.
# вес изделия станка №1
mu_1_2 = 14.
# стандартные отклонения
sigma_1_1 = 3.5
sigma_1_2 = 1.

# диаметр изделия станка №2
mu_2_1 = 52.
# вес изделия станка №2
mu_2_2 = 9.5
# стандартные отклонения
sigma_2_1 = 2.
sigma_2_2 = 0.7


Проведем расчет 
X = np.zeros((N, m))
np.random.seed(seed=42)
# инициализируем данные по деталям, производства станка №1
X[:N1, 0] = np.random.normal(loc=mu_1_1, scale=sigma_1_1, size=N1)
X[:N1, 1] = np.random.normal(loc=mu_1_2, scale=sigma_1_2, size=N1)
# инициализируем детали, производства станка №2
X[N1:N, 0] = np.random.normal(loc=mu_2_1, scale=sigma_2_1, size=N2)
X[N1:N, 1] = np.random.normal(loc=mu_2_2, scale=sigma_2_2, size=N2)

# зафиксируем правильные ответы (для оценки качества алгоритма, в обучении не используется)
y = np.zeros((N))
y[:N1] = np.array((1))
y[N1:N] = np.array((2))

# запишем средние значения диаметра и веса изделий в матричном формате (для удобства расчетов)
mu  = np.array(([mu_1_1, mu_1_2], [mu_2_1, mu_2_2]))

# запишем стандартные отклонения в формате матрицы ковариации (для удобства расчетов)
sigma = np.array(([sigma_1_1, 0.],[0., sigma_1_2], [sigma_2_1, 0.],[0., sigma_2_2]))
sigma = sigma.reshape(k, m, m)

# инициализируем априорную вероятность извлечь изделие, произведенное на станке №1 и №2
w = np.array([float(1./k), float(1./k)])

# запустим наши функции
pj_xi = gaus_func_02(k, m, X, mu, sigma)
proba_X = proba_func_02(pj_xi, w, m)

# установим порог вероятности, при достижении которого, изделие будет относиться к тому или иному станку
limit_proba = 0.5

pred_X = pred_x_02(proba_X, limit_proba)
        
# определим качество нашего алгоритма
print 'Доля верно определенных изделий:', round(accuracy_score(y, pred_X),3)
print

graph_02_algorithm(pred_X, mu)

graph_02_true(X, mu)


График №2.1 «Распределение изделий в соответствии с алгоритмом»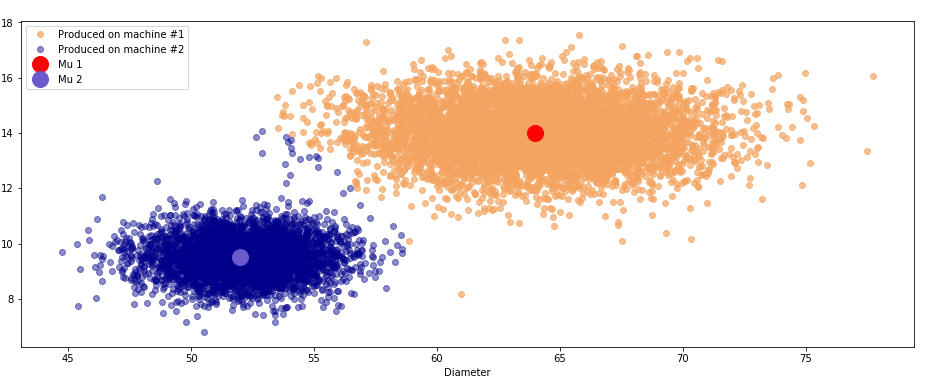
qtw_twczfz95bc_vbno56cmiyvs.png

График №2.2 «Истинное распределение изделий»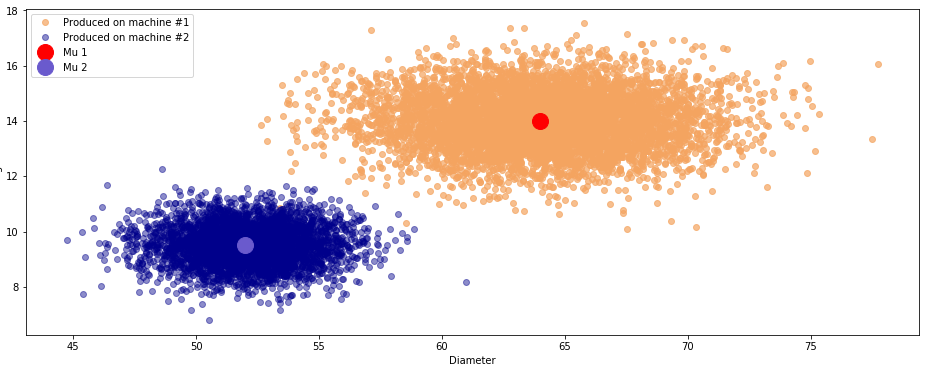
otkdh2bikyfzqkvvzhb_-6vdfpe.png

По аналогии с предыдущим примером мы сгенерировали 10000 значений в соответствии с указанными выше параметрами $\mu$ и $\sigma$, написали несколько функций для работы нашего алгоритма и запустили его. Принципиальное отличие этого кода от кода из предыдущего примера состоит в том, что мы использовали на этот раз матричные выражения для проведения вычислений.

В результате наш алгоритм показывает долю правильных ответов равную 0.998, что собственно весьма неплохо.

Проблемы как мы видим, все там же — ошибки в деталях, которые были произведены на разных станках и при этом имеют схожие размеры и вес.

Код написан таким образом, чтобы читатель смог подставить любые значения параметров $\mu$ и $\sigma$ и посмотреть, как будет работать алгоритм: в каких случаях качество будет ухудшаться, в каких улучшаться. Главное при этом не забывать изучать график. Ну, а мы двигаемся к нашему конечному пункту разбора EM-алгоритма, собственно самому EM-алгоритму.

Встречаем EM-алгоритм

Продолжим наш пример с поступившими на склад деталями. Но на этот раз мы будем знать только то, что изделия были произведены на двух различных станках, их 10000, каждая деталь имеет диаметр и размер и более ничего нам не известно. Но задание не изменилось — нам также, как и раньше, из всей большой кучи, случайно перемешанных изделий, нужно будет определить к какому станку относится та или иная деталь.

На первый взгляд звучит почти не реально, но на самом деле у нас в руках мощный инструментарий: формула Байеса и формула плотности вероятности случайной величины. Давайте всем этим добром и воспользуемся.

Решение

Как мы поступим? Как и положено в EM-алгоритме мы для начала инициализируем параметры:

Вероятность гипотезы извлечь деталь, произведенную на станке №1 — $w_1$ мы определим равной вероятности гипотезы извлечь деталь, произведенной на станке №2 — $w_2$. Гипотез всего две, а значит каждая из них на первом шаге будет равна 0.5.

Математическое ожидание случайных величин $\mu$ определим следующим образом. Перемешаем все изделия с помощью функции random, поделим совокупность поровну на две части, для каждой части по каждому параметру (диаметр, вес) определим среднее значение.

Стандартное отклонение $\sigma$ возьмем, что называется с потолка — установим его равным единице по всем параметрам. Запишем в формате матрицы ковариации.

Мы готовы сделать первый E-шаг алгоритма. Используя инициализированные параметры случайных величин, определяем вероятность каждой детали быть отнесенной к станку №1 или станку №2.

Собственно, таким образом, мы сделали первый E-шаг.

Теперь дело за M-шагом. Здесь все просто. После того, как мы определили вероятность каждой детали быть произведенной на том или ином станке, мы можем заново пересчитать вероятность каждой гипотезы — $w_1$, $w_2$, а также $\mu$ и $\sigma$.

Таких итераций, по два шага каждая, мы сделаем 15.

Смотрим код.

Функции, используемые в работе EM-алгоритма 
# запишем функцию E-шага
def e_step(x, k, m, n, w, mu, sigma):
    # инициализируем массив плотностей вероятностей извлечения i-ой детали из произведенных на j-м станке 
    pj_xi = []
    for j in range(k):
        det_sigma_j = np.linalg.det(sigma[j])
        factor_1 = 1 / (((2 * math.pi)**(k/2)) * ((det_sigma_j)**0.5))
        factor_2 = []
        for i in x:
            factor_2.append(math.e**float(
                -0.5 * np.matrix(i - mu[j]) * np.matrix(np.linalg.inv(sigma[j])) * np.matrix(i - mu[j]).T))
        pj_xi.append(factor_1 * np.array(factor_2))
    pj_xi = np.array(pj_xi)
    
    # инициализируем массив плотностей вероятностей того, что i-я деталь произведена на j-м станке
    pj_xi_w = []
    for j in range(k):
        pj_xi_w.append(pj_xi[j] * w[j])
    pj_xi_w = np.array(pj_xi_w)
    
    # рассчитае
    
            
© Habrahabr.ru