Равномощные отрезки… или исповедь сумасшедшего
Читая несколько лет назад «Начала теории множеств» Шеня, столкнулся с одним показательным примером, представленным в пункте — «Равномощные множества», который, видимо, и самого автора (Шеня) несколько удивлял, раз он обращал на него внимание.
В указанном пункте автор (Шень) утверждал что принято считать два отрезка с длинами в одну и две единицы равномощными в силу функциональной, взаимно однозначной соотнесённости (соответствия) элементов. Действительно, если любое число из первого отрезка умножить на 2, то мы получил число, принадлежащее второму отрезку, что и «доказывает» эту соотнесённость.
Возникает ряд замечаний, которые призваны установить несправедливость такого положения
Прежде всего, как многим известно, количество выявляемых чисел на каждом из отрезков бесконечно много исходя из математического подхода, но при нём не определены принципы их выявления. В худшем представлении, они могут просто определяться как ЛЮБЫЕ, не превышающие установленной границы отрезка. Этот случай будет снова подчёркнут в конце статьи.
Но что если попытаться определять на отрезках числа, исходя из постепенного увеличения их единиц деления? Таким образом, я могу выявлять бесконечное количество чисел на обоих отрезках и проверять их сопоставимость через индукцию.
Определяя на отрезках исключительно целые значения, у меня отсутствует полная сопоставимость: на отрезке длины два есть число 1, которое не связано функционально (через умножение на 2) ни с одним числом из отрезка длины один.
Определяя на отрезках дробные значения с делителем 2, у меня количество несопоставляемых элементов увеличивается вдвое: на втором отрезке такими числами будут ½ и 3/2.
И так далее.
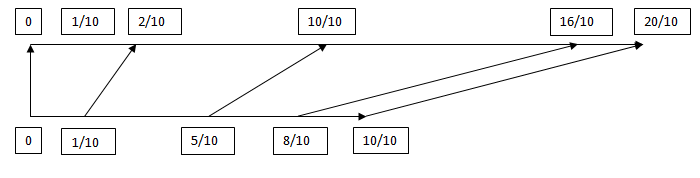
Постепенное увеличение единиц деления отрезков выявляет, при каждом таком изменении меры, всё больше несоответствий, которые нарушают указанную равномощность. Оказывается, принятое положение равномощности двух отрезков опирается на некоторую неопределённость, которая даже по сути является логической ошибкой, тяжело проявляемой при рассмотрении. Взяв ЛЮБОЕ число из первого отрезка, мы пытаемся его сопоставлять с ЛЮБЫМ числом второго, что невозможно при разных единицах деления этих отрезков. Более того, если мы коснёмся трактовки отрезков, как актуальных бесконечностей, по составу своих элементов, то выделяя на них как разумные (рациональные) числа, так и целые, уже при выделении целых чисел получаются несоответствия, что указано выше для полной совокупности частных случаев, рассматриваемых через индукцию (в совокупности они представляют множество разумных (рациональных) чисел на отрезках).
Известно, что из представления разумных (рациональных) чисел можно получать и неразумные (иррациональные), путём применения алгебраических операций над первыми по категории. Следовательно, применяя алгебраические операции над разумными (рациональными), элементами обоих отрезков при текущей единице деления, мы получим всё то же несоответствие элементов двух отрезков.
Таким образом, используя трансфинитную индукцию, автор статьи может обратиться и к рассмотрению бесконечного числа действительных чисел, исходя из трактовки последних, выявляя и их несоответствие тоже, при ВСЕХ единицах деления данных отрезков на самих этих отрезках.
Можно ли считать два множества равномощными, если у них строго не определены наличествующие элементы или хотя бы функция, их задающая? Нет.
