Распределение Пуассона и футбольные ставки

Если объединить статистические данные спортивных соревнований с распределением Пуассона, то можно рассчитать вероятное количество мячей, которые будут забиты во время футбольной игры. На этом основании можно понять откуда берутся букмекерские ставки, а также научиться самостоятельно их рассчитывать с помощью R.
В конце XIX в. русский экономист и статистик польского происхождения Владислав Борткевич, проанализировав данные в 14 корпусах прусской армии за 20 лет, придумал способ предсказывать случаи гибели солдат от удара копытом лошади. Для этого он одним из первых использовал на практике распределение Пуассона. Результаты его расчетов показаны в таблице.
| Смертность от удара лошади | Согласно формуле Пуассона | Наблюдения |
|---|---|---|
| 0 | 108.67 | 109 |
| 1 | 66.29 | 65 |
| 2 | 20.22 | 22 |
| 3 | 4.11 | 3 |
| 4 | 0.63 | 1 |
| 5 | 0.08 | 0 |
| 6 | 0.01 | 0 |
Как видим теоретико-вероятностные вычисления отлично сочетаются с реальными данными. Можно ли применить этот способ в ставках на спорт, чтобы развлечься и заработать?
Формула Пуассона
В классическом учебнике по теории вероятностей Б В. Гнеденко дается такое определение теоремы Пуассона.

Если же говорить простым языком, то на основе этой формулы можно рассчитать распределение вероятностей для событий, которые:
- происходят за единицу времени или на единицу площади;
- дискретны, их можно пронумеровать;
- независимы друг от друга;
- не имеют верхней границы, по крайней мере — теоретической;
Можно привести уйму примеров из повседневной жизни: количество пострадавших от удара молнии, от ДТП, количество рекламных звонков и сообщений, число поломок лифта за год, изюминок в пасхальном куличе и т. д. Для нас же интерес представляют примеры из спорта.
Футбольная статистика
Оказывается, количество забитых мячей в футбольном матче очень хорошо вписывается в Пуассоново распределение. Так, на диаграмме слева мы видим число голов, забитых каждой командой в каждом из 380 матчей чемпионата Испании 2008–2009 годов. На диаграмме справа подсчитаны теоретические данные модели.
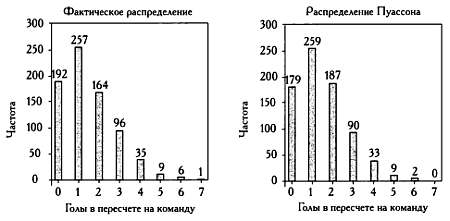
Диаграммы очень похожи, следовательно модель Пуассона хорошо объясняет соотношение мячей, забитых командой в течение матча.
Теперь немного о спортивных ставках. Те, кто захаживает в букмекерские конторы, может увидеть их на табло. Вот, как выглядят некоторые ставки на игру команд английской Премьер-Лиги в ближайший понедельник.
| Англия — Премьер-лига | 1 | x | 2 |
|---|---|---|---|
| Манчестер Юнайтед — Сандерленд | 1,25 | 6,80 | 15,00 |
| Челси — Борнмут | 1,39 | 5,10 | 10,50 |
| Халл — Манчестер Сити | 10,50 | 5,80 | 1,35 |
1 — победа первой команды
x — ничья
2 — победа другой команды.
Достаточно мельком взглянуть на турнирную таблицу и станет понятно, почему так высоки ставки и возможный выигрыш в случае победы Сандерленда над Манчестер Юнайтед. За каждый фунт стерлингов в этом случае можно заработать 15 фунтов стерлингов, с фантастическими 1400% прибыли. В случае же победы команды Манчестер Юнайтед выигрыш будет всего 1,25 фунтов стерлингов, прибыль составит всего 25%.
Попробуем теперь сами рассчитать ставки на игру Манчестер Юнайтед против Манчестер Сити, которая должна состояться 26-го февраля 2017 г. Несмотря на то, что у двух клубов названия похожи, МС играет на своем поле, а МЮ — в гостях.
Прежде чем воспользоваться формулой Пуассона надо рассчитать значение µ, а для этого надо получить среднее количество забитых и пропущенных мячей участников игры относительно среднего для всех команд.
µMU — Ожидаемое количество забитых мячей для Манчестер Юнайтед
µMC — Ожидаемое количество забитых мячей для Манчестер Сити
Тогда
- µMU = нападение МЮ ✕ оборона МС ✕ среднее количество забитых на выездных матчах.
- µMC = нападение МС ✕ оборона МЮ ✕ среднее количество забитых голов на своем поле.
За весь сезон 2015/2016 было 380 футбольных игр, в которых команды у себя дома забили 567 мяча (1.49 за игру), а в гостях — 459 (1.20 за игру).
(5:563)$ echo 'scale=5;567/380;459/380' | bc -q
1.49210
1.20789Далее, считаем коэффициенты нападения МЮ, нападения МC, оборона МЮ и обороны МС.
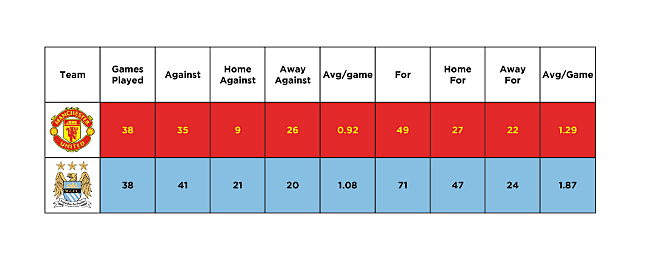
На выездных матчах Манчестер Юнайтед забивал в среднем 1.15 мячей за игру, а пропускал — 1.36.
(5:552)$ echo 'scale=5;22/19;26/19' | bc -q
1.15789
1.36842У себя дома Манчестер Сити забивал в среднем 2.47 мячей за игру, а пропускал — 1.10.
(5:553)$ echo 'scale=5;47/19;21/19' | bc -q
2.47368
1.10526Теперь те же самые значения мы взвешиваем относительно общих средних значений. Относительное среднее нападения МЮ на чужом поле равно 0.958, а относительное среднее обороны МС на своем поле — 0.915.
(5:554)$ echo 'scale=5;22/19/1.20789;21/19/1.20789' | bc -q
.95860
.91503Относительное среднее обороны МЮ на чужом поле равно 0.917, а относительное среднее нападения МС на своем поле — 1.657.
(5:555)$ echo 'scale=5;26/19/1.49210;47/19/1.49210' | bc -q
.91711
1.65785И наконец, перемножая все промежуточные средние значения, находим µ.
µMU = 1.06
µMC = 2.27
(5:556)$ echo 'scale=5;.95860*.91503*1.20789;1.65785*.91711*1.49210' |bc -q
1.05948
2.26863Голы по Пуассону
Теперь мы можем посчитать вероятности на разные исходы этой встречи. В R это делается очень просто, но можно срезать углы и воспользоваться статистическим онлайн калькулятором.
> dpois(x=(0:5), lambda=2.26863)
[1] 0.10345381 0.23469843 0.26622195 0.20131970 0.11417998 0.05180642
> dpois(x=(0:5), lambda=1.05948)
[1] 0.346636014 0.367253924 0.194549094 0.068706958 0.018198412 0.003856171Итак, вероятности распределены следующим образом.
| Голы | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| МЮ | 34.663% | 36.725% | 19.454% | 6.870% | 1.819% | 0.385% |
| МС | 10.345% | 23.469% | 26.622% | 20.131% | 11.417% | 5.180% |
Вероятность того, что Манчестер Юнайтед не забьет ни одного гола составляет 34.663%, то же самое для Манчестер Сити — 10.345%, вероятность нулевого исхода встречи равна их произведению и составляет 3.586%. Матрица всех результатов от 0:0 до 5:5.
> a=dpois(x=(0:5), lambda=1.05948)
> b=dpois(x=(0:5), lambda=2.26863)
> A=a%*%t(b)
> A
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.0358608180 0.0813549276 0.092282115 0.0697846579 0.0395788921 0.0179579724
[2,] 0.0379938195 0.0861939186 0.097771055 0.0739354494 0.0419330446 0.0190261126
[3,] 0.0201268459 0.0456603665 0.051793239 0.0391665649 0.0222136111 0.0100788929
[4,] 0.0071079969 0.0161254150 0.018291300 0.0138320641 0.0078449589 0.0035594618
[5,] 0.0018826951 0.0042711387 0.004844817 0.0036636988 0.0020778943 0.0009427947
[6,] 0.0003989356 0.0009050372 0.001026597 0.0007763231 0.0004402975 0.0001997744Попробуем теперь рассчитать вероятность победы каждой из сторон, вероятность ничейного исхода и наконец определимся со ставками. Начнем с ничейного результата. Перемножаем векторы событий для МЮ и МС, и считаем сумму диагональной матрицы. Ставка 1 к 5.264.
> sum(diag(A))
[1] 0.1899577
> 1/sum(diag(A))
[1] 5.26433Шансы победы МС равны сумме всевозможных 1:0, 2:0, … 5:0, 2:1, 3:1, … и т. д. до 5:4. Ставка равна 1.619.
sum(A[1,2:6])+sum(A[2,3:6])+sum(A[3,4:6])+sum(A[4,5:6])+A[5,6]
[1] 0.6174305
1/(sum(A[1,2:6])+sum(A[2,3:6])+sum(A[3,4:6])+sum(A[4,5:6])+A[5,6])
1.619615Шансы победы МЮ поменьше, соответственно побольше будет ставка и денежный выигрыш — 1 к 5.191.
> 1 - (sum(A[1,2:6])+sum(A[2,3:6])+sum(A[3,4:6])+sum(A[4,5:6])+A[5,6] + sum(diag(A)))
[1] 0.1926118
> 1/(1 - (sum(A[1,2:6])+sum(A[2,3:6])+sum(A[3,4:6])+sum(A[4,5:6])+A[5,6] + sum(diag(A))))
[1] 5.19179Ставки сделаны!
| Ставки на игру | 1 | x | 2 |
|---|---|---|---|
| Манчестер Сити — Манчестер Юнайтед | 1.620 | 5.264 | 5.192 |
Конечно, модель Пуассона довольно проста и не учитывает множество факторов и обстоятельств: новый игрок, новый тренер, статус матча, обстоятельства клуба и т. д. Тем не менее Elihu Feustel умудряется на ставках зарабатывать миллионы, используя математические алгоритмы.
Использованные материалы
- How to calculate football betting odds using Poisson Distribution
- Распределение Пуассона на примере футбольных ставок
- Football stats and results
- Абсолютная точность и другие иллюзии. Секреты статистики
