Работа с временными рядами в Python. Часть 1

Аналитика данных стала неотъемлемой частью современного бизнеса и научных исследований. И одним из ключевых аспектов анализа данных являются временные ряды. Эффективная работа с временными рядами играет критическую роль в прогнозировании, стратегическом планировании и принятии решений в различных отраслях.
Временные ряды — это наборы данных, где каждая точка данных связана с определенным моментом времени. Это может быть что угодно, от ежедневных финансовых показателей до ежечасных кликов на веб-сайте или даже месячных показателей погоды. Зачем нам это нужно? Потому что временные ряды предоставляют нам ценную информацию о том, как меняются данные со временем.
Области, где временные ряды играют решающую роль:
1. Финансовая аналитика: Прогнозирование цен акций, анализ рыночных тенденций и определение оптимального времени для инвестиций.
2. Маркетинг и анализ пользовательской активности: Отслеживание изменений в поведении пользователей на веб-сайте, прогнозирование спроса на товары и услуги.
3. Прогнозирование спроса: Определение оптимального уровня запасов, чтобы избежать дефицита или избытка товаров.
4. Анализ временных данных о заболеваниях: Оценка распространения эпидемий, прогнозирование заболеваемости и смертности.
5. Климатические исследования: Изучение изменений в климатических параметрах, таких как температура и осадки, для анализа климатических тенденций.
6. Прогнозирование трафика: Анализ и прогнозирование трафика на веб-сайтах и в сетях.
7. Промышленное оборудование и обслуживание: Предсказание времени отказа оборудования и оптимизация производственных процессов.
Временные ряды также присутствуют в повседневной жизни: температурные измерения, динамика финансовых индексов или даже ежедневные показатели физической активности с помощью носимых устройств — все это временные ряды.
Временные ряды могут быть стационарными (когда статистические характеристики, такие как среднее и дисперсия, остаются постоянными во времени) или нестационарными (когда эти характеристики изменяются с течением времени). Понимание природы временного ряда важно для выбора подходящих методов анализа.
Основные характеристики временных рядов
Тренд: Тренд представляет собой долгосрочное изменение в данных. Это может быть рост или спад. Например, если продажи вашей компании растут каждый месяц в течение года, это будет проявление тренда.
Сезонность: Сезонность — это циклические изменения данных, которые повторяются с постоянным интервалом времени. Например, продажи игрушек могут расти перед праздниками и падать после них.
Шум: Шум представляет собой случайные колебания данных, которые не подчиняются определенным закономерностям. Это может быть вызвано различными факторами, такими как случайные события или ошибки измерения.
Циклы: Циклы — это долгосрочные колебания данных, которые не связаны с сезонностью. Например, экономические циклы могут вызывать волны роста и спада в продажах.
Стационарность: Стационарный временной ряд — это ряд, в котором статистические характеристики, такие как среднее и дисперсия, остаются постоянными с течением времени. Многие методы анализа временных рядов предполагают стационарность данных.
Автокорреляция: Автокорреляция — это корреляция между значениями ряда в разные моменты времени. Она может помочь выявить закономерности в данных.
Пропущенные значения: Временные ряды могут содержать пропущенные значения, которые требуется обработать перед анализом.
Прежде чем мы начнем работу, нам нужно убедиться, что у нас есть все необходимые библиотеки для анализа временных рядов:
1. pandas: Pandas — это библиотека для работы с данными, которая предоставляет удобные структуры данных, такие как DataFrame, и множество функций для анализа и манипуляции данными. Она идеально подходит для работы с временными рядами, так как позволяет легко хранить и анализировать временные данные.
2. numpy: NumPy — это библиотека для работы с массивами и матрицами чисел. Она полезна при выполнении вычислений над данными временных рядов.
3. matplotlib и seaborn: Эти библиотеки позволяют создавать графики и визуализации данных, что особенно важно при анализе временных рядов.
4. statsmodels: Statsmodels — это библиотека для статистического анализа данных. Она содержит множество методов для анализа временных рядов, включая модели ARIMA и SARIMA.
5. scikit-learn: Scikit-learn предоставляет множество инструментов для машинного обучения, включая модели регрессии и классификации, которые можно использовать для анализа временных рядов.
Устанавливаем:
!pip install pandas numpy matplotlib seaborn statsmodels scikit-learn
Теперь, когда у нас есть необходимые библиотеки, давайте перейдем к работе с датами и временем.
Одной из ключевых характеристик временных рядов является наличие временных меток, которые позволяют нам связывать данные с конкретными моментами времени. При работе с временными рядами необходимо уметь обращаться с датами и временем.
Для начала давайте создадим небольшой dataset с данными о продажах электроники за несколько месяцев. Для примера давайте представим, что у нас есть следующие данные:
import pandas as pd
data = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, 1200, 1300, 1100, 1400]}
df = pd.DataFrame(data)
# Преобразуем столбец 'Дата' в формат даты
df['Дата'] = pd.to_datetime(df['Дата'])
print(df)
Результат будет следующим:
Дата Продажи
0 2023-01-01 1000
1 2023-02-01 1200
2 2023-03-01 1300
3 2023-04-01 1100
4 2023-05-01 1400
Теперь у нас есть DataFrame с данными о продажах и столбцом 'Дата', который имеет тип datetime64. Это позволяет нам выполнять различные операции, такие как выбор данных по дате или вычисление временных интервалов.
Пример:
# Выбор данных по диапазону дат
subset = df[(df['Дата'] >= '2023-03-01') & (df['Дата'] <= '2023-04-30')]
print(subset)
Вывод:
Дата Продажи
2 2023-03-01 1300
3 2023-04-01 1100
Таким образом, работа с датами и временем в pandas позволяет нам легко фильтровать и анализировать данные временных рядов.
Обработка пропущенных значений
Пропущенные значения — это обычное явление при работе с данными временных рядов. Они могут возникать по разным причинам, например, из-за ошибок при сборе данных или временных перерывов в измерениях. Поэтому важно знать, как обрабатывать пропущенные значения.
Давайте рассмотрим, как можно обработать пропущенные значения в DataFrame с помощью pandas. Для примера допустим, что у нас есть следующий dataset:
import pandas as pd
data = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, None, 1300, 1100, 1400]}
df = pd.DataFrame(data)
# Преобразуем столбец 'Дата' в формат даты
df['Дата'] = pd.to_datetime(df['Дата'])
print(df)
Результат:
Дата Продажи
0 2023-01-01 1000.0
1 2023-02-01 NaN
2 2023-03-01 1300.0
3 2023-04-01 1100.0
4 2023-05-01 1400.0
Как видите, у нас есть пропущенное значение (NaN) в столбце 'Продажи'. Существует несколько способов обработки таких значений:
1. Удаление строк с пропущенными значениями:
df.dropna(inplace=True)
Этот метод удаляет строки, содержащие пропущенные значения. Важно помнить, что это может привести к потере данных.
2. Замена пропущенных значений:
df.fillna(0, inplace=True)
Здесь мы заменяем все пропущенные значения на 0. Вы можете выбрать другое значение для замены вместо 0 в зависимости от контекста.
3. Интерполяция:
df.interpolate(inplace=True)
Интерполяция позволяет заполнить пропущенные значения на основе соседних значений. Это может быть полезно, если данные имеют некоторую структуру.
Обработка пропущенных значений зависит от конкретной задачи и данных временных рядов. Важно выбирать подходящий метод в каждом случае.
Мы переходим к разделу анализа временных рядов, который поможет нам раскрывать информацию и закономерности, скрытые в данных. Этот этап позволяет нам понять структуру временных рядов, определить их стационарность и выделить основные компоненты, такие как тренд, сезонность и шум.
Стационарность временных рядов
Стационарность — одно из важнейших свойств временных рядов. Стационарный ряд — это ряд, в котором статистические характеристики, такие как среднее и дисперсия, остаются постоянными во времени. Это свойство позволяет нам строить надежные модели и прогнозировать будущие значения.
1. Тесты на стационарность:
Первый шаг в анализе временных рядов — проверка стационарности. Для этого существует несколько статистических тестов. Один из них — тест Дики-Фуллера. Давайте применим его к нашему небольшому dataset с данными о продажах в условном филиале МВидео:
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
# Создаем dataset с данными о продажах
data = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, 1200, 1300, 1100, 1400]}
df = pd.DataFrame(data)
# Преобразуем столбец 'Дата' в формат даты
df['Дата'] = pd.to_datetime(df['Дата'])
# Построим график продаж
plt.plot(df['Дата'], df['Продажи'])
plt.title('Продажи в магазине МВидео')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.show()
# Проведем тест Дики-Фуллера на стационарность
result = adfuller(df['Продажи'])
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))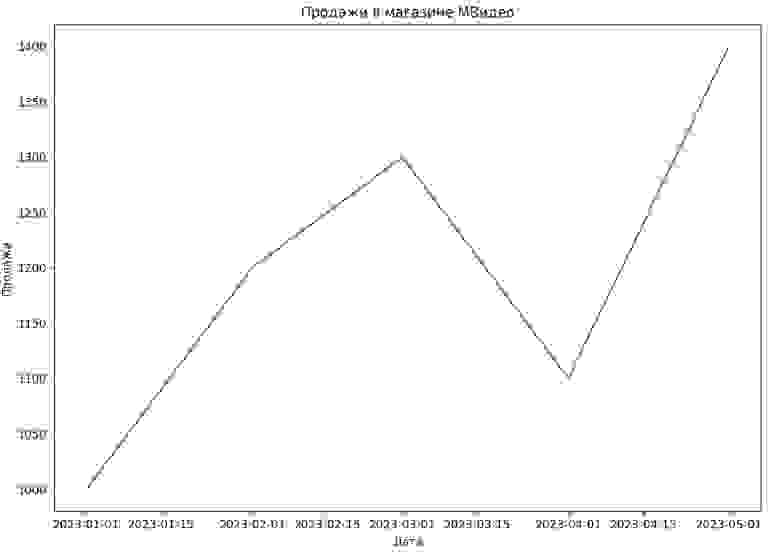
На выходе мы получим статистику теста Дики-Фуллера и p-значение. Если p-значение меньше уровня значимости (обычно 0.05), то мы можем отклонить нулевую гипотезу о нестационарности ряда и считать его стационарным.
2. Преобразование ряда для достижения стационарности:
Если начальный ряд не является стационарным, то его можно преобразовать. Например, можно вычесть тренд и сезонные компоненты, чтобы получить стационарный остаток.
# Преобразование для удаления тренда
df['Продажи_без_тренда'] = df['Продажи'] - df['Продажи'].rolling(window=2).mean()
# Преобразование для удаления сезонности (в данном случае просто разница между текущим и предыдущим значением)
df['Продажи_стационарные'] = df['Продажи_без_тренда'].diff()
# Удалим первые строки с пропущенными значениями
df.dropna(inplace=True)
# Построим графики
plt.plot(df['Дата'], df['Продажи_без_тренда'], label='Без тренда')
plt.plot(df['Дата'], df['Продажи_стационарные'], label='Стационарные')
plt.legend()
plt.title('Преобразованные продажи')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.show()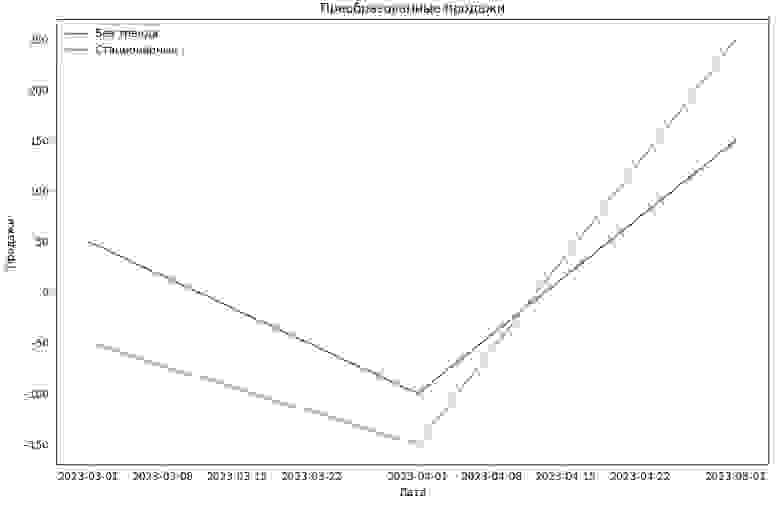
Теперь у нас есть стационарный ряд Продажи_стационарные, который мы можем анализировать и моделировать.
Компоненты временных рядов
Временные ряды обычно состоят из трех основных компонентов: тренда, сезонности и шума (остатка). Понимание этих компонентов помогает нам лучше понимать структуру ряда и выбирать подходящие методы анализа.
1. Тренд:
Тренд — это долгосрочное изменение в данных, которое может быть восходящим (рост), нисходящим (падение) или горизонтальным (без изменений). Он представляет собой общее направление движения данных.
Посмотрим на примере:
# Создаем dataset с данными о продажах с трендом
data_trend = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, 1200, 1400, 1600, 1800]}
df_trend = pd.DataFrame(data_trend)
# Преобразуем столбец 'Дата' в формат даты
df_trend['Дата'] = pd.to_datetime(df_trend['Дата'])
# Построим график продаж с трендом
plt.plot(df_trend['Дата'], df_trend['Продажи'])
plt.title('Продажи с трендом (рост)')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.show()
На графике видно, что продажи увеличиваются со временем. Это пример тренда восходящего направления.
2. Сезонность:
Сезонность — это периодические колебания в данных, которые повторяются через равные временные интервалы. Сезонность может быть годовой, месячной, недельной и т. д. Она связана с событиями, которые регулярно влияют на данные.
# Создаем dataset с данными о продажах с сезонностью
data_seasonal = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, 1200, 900, 1100, 1400]}
df_seasonal = pd.DataFrame(data_seasonal)
# Преобразуем столбец 'Дата' в формат даты
df_seasonal['Дата'] = pd.to_datetime(df_seasonal['Дата'])
# Построим график продаж с сезонностью
plt.plot(df_seasonal['Дата'], df_seasonal['Продажи'])
plt.title('Продажи с сезонностью')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.show()
На графике видно, что продажи имеют периодические колебания, которые повторяются примерно каждый месяц.
3. Шум:
Шум (остаток) — это случайные изменения в данных, которые не могут быть объяснены трендом или сезонностью. Он представляет собой нерегулярные колебания и вариации в данных.
# Создаем dataset с данными о продажах с шумом
data_noise = {'Дата': ['2023-01-01', '2023-02-01', '2023-03-01', '2023-04-01', '2023-05-01'],
'Продажи': [1000, 1200, 1050, 1150, 1100]}
df_noise = pd.DataFrame(data_noise)
# Преобразуем столбец 'Дата' в формат даты
df_noise['Дата'] = pd.to_datetime(df_noise['Дата'])
# Построим график продаж с шумом
plt.plot(df_noise['Дата'], df_noise['Продажи'])
plt.title('Продажи с шумом')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.show()
На графике видно, что продажи имеют случайные колебания, которые не имеют явного тренда или сезонности. Это пример шума.
Автокорреляция и частичная автокорреляция
Автокорреляция — это мера корреляции между временным рядом и его лагированными (отстающими) значениями. Это позволяет нам определить зависимость текущих значений от предыдущих.
Частичная автокорреляция — это мера корреляции между временным рядом и его лагированными значениями с учетом корреляции в промежуточных лагах. Она помогает выявить «чистую» зависимость от определенных отстающих значений, исключая влияние промежуточных лагов.
Представим, что у нас есть временной ряд данных о температуре каждый час:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# Создаем небольшой временной ряд температуры
np.random.seed(0)
dates = pd.date_range(start='2023-01-01', end='2023-01-07', freq='H')
temperature = np.random.normal(loc=25, scale=5, size=len(dates))
df_temperature = pd.DataFrame({'Дата': dates, 'Температура': temperature})
# Устанавливаем 'Дата' в качестве индекса
df_temperature.set_index('Дата', inplace=True)
# Построим график временного ряда
plt.figure(figsize=(12, 4))
plt.plot(df_temperature.index, df_temperature['Температура'])
plt.title('Временной ряд температуры')
plt.xlabel('Дата и время')
plt.ylabel('Температура (°C)')
plt.grid(True)
plt.show()
# Рассчитываем автокорреляцию и частичную автокорреляцию
plt.figure(figsize=(12, 6))
plt.subplot(211)
plot_acf(df_temperature['Температура'], lags=50, ax=plt.gca())
plt.title('Автокорреляция')
plt.subplot(212)
plot_pacf(df_temperature['Температура'], lags=50, ax=plt.gca())
plt.title('Частичная автокорреляция')
plt.tight_layout()
plt.show()
На графиках автокорреляции и частичной автокорреляции вы можете увидеть значимые лаги, которые могут помочь в выборе параметров модели для анализа и прогнозирования временного ряда температуры. Эти графики помогают определить структуру и зависимости в данных.
В этом разделе мы рассмотрим несколько практических примеров использования анализа временных рядов для решения разнообразных задач.
Прогнозирование продаж на основе временных рядов продаж электроники
В этом примере мы будем использовать данные о ежемесячных продажах электроники в магазине МВидео для прогнозирования будущих продаж.
Cоздадим небольшой dataset с данными о продажах. В качестве исходных данных предположим следующие продажи за последние два года:
import pandas as pd
import numpy as np
# Создаем даты с января 2022 года по декабрь 2023 года
dates = pd.date_range(start='2022-01-01', end='2023-12-31', freq='M')
# Генерируем случайные продажи в интервале от 1000 до 5000
sales = np.random.randint(1000, 5000, size=len(dates))
# Создаем DataFrame
sales_df = pd.DataFrame({'Дата': dates, 'Продажи': sales})
# Устанавливаем 'Дата' в качестве индекса
sales_df.set_index('Дата', inplace=True)
# Выводим первые несколько строк
print(sales_df.head())
Результат:
Продажи
Дата
2022-01-31 1355
2022-02-28 4665
2022-03-31 3154
2022-04-30 3490
2022-05-31 3569Визуализация данных
Перед тем как перейти к прогнозированию, давайте визуализируем данные о продажах, чтобы понять их структуру и особенности.
import matplotlib.pyplot as plt
# Построим график продаж
plt.figure(figsize=(12, 6))
plt.plot(sales_df.index, sales_df['Продажи'], marker='o', linestyle='-')
plt.title('Продажи в магазине МВидео')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.grid(True)
plt.show()
На графике видно, что у нас есть временной ряд продаж с некоторыми трендами и колебаниями.
Подготовка данных
Прежде чем перейти к прогнозированию, нам нужно подготовить данные. Это включает в себя обработку пропущенных значений и проверку стационарности ряда.
# Обработка пропущенных значений (если они есть)
sales_df.dropna(inplace=True)
# Проверка стационарности ряда
from statsmodels.tsa.stattools import adfuller
result = adfuller(sales_df['Продажи'])
print('ADF статистика:', result[0])
print('p-значение:', result[1])
print('Критические значения:')
for key, value in result[4].items():
print(f' {key}: {value}')
Результат:
ADF статистика: -3.336001912478917
p-значение: 0.013343910713214318
Критические значения:
1%: -3.859073285322359
5%: -3.0420456927297668
10%: -2.6609064197530863
Если p-значение ниже некоторого порогового значения (обычно 0.05), то мы можем считать ряд стационарным.
Выбор и обучение модели
После подготовки данных мы можем выбрать и обучить модель для прогнозирования. Для этого примера мы будем использовать модель ARIMA.
from statsmodels.tsa.arima.model import ARIMA
# Обучение модели ARIMA
model = ARIMA(sales_df['Продажи'], order=(1, 1, 1))
model_fit = model.fit()
# Вывод статистики модели
print(model_fit.summary())
Результат:
SARIMAX Results
==============================================================================
Dep. Variable: Продажи No. Observations: 24
Model: ARIMA(1, 1, 1) Log Likelihood -197.611
Date: Mon, 18 Sep 2023 AIC 401.222
Time: 12:03:31 BIC 404.628
Sample: 01-31-2022 HQIC 402.078
- 12-31-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.1787 0.252 0.709 0.478 -0.315 0.673
ma.L1 -1.0000 0.349 -2.868 0.004 -1.683 -0.316
sigma2 1.469e+06 2.37e-07 6.19e+12 0.000 1.47e+06 1.47e+06
===================================================================================
Ljung-Box (L1) (Q): 0.05 Jarque-Bera (JB): 0.87
Prob(Q): 0.82 Prob(JB): 0.65
Heteroskedasticity (H): 0.70 Skew: 0.34
Prob(H) (two-sided): 0.63 Kurtosis: 2.33
===================================================================================
Оценка качества прогноза
После обучения модели мы можем оценить ее качество на основе имеющихся данных.
from sklearn.metrics import mean_squared_error, mean_absolute_error
# Прогноз на основе обученной модели
forecast = model_fit.forecast(steps=12)
# Рассчитываем MSE и MAE
mse = mean_squared_error(sales_df['Продажи'][-12:], forecast)
mae = mean_absolute_error(sales_df['Продажи'][-12:], forecast)
print(f'MSE: {mse}')
print(f'MAE: {mae}')
Результат:
MSE: 1178795.2830408707
MAE: 906.8571433244668Прогноз на будущее
Теперь, когда модель обучена и ее качество оценено, мы можем использовать ее для прогнозирования будущих значений.
# Прогноз на будущее (следующие 12 месяцев)
forecast_future = model_fit.forecast(steps=12)
# Создаем новый DataFrame для будущих значений
future_dates = pd.date_range(start='2024-01-01', periods=12, freq='M')
forecast_df = pd.DataFrame({'Дата': future_dates, 'Прогноз продаж': forecast_future})
# Присоединяем прогноз к исходному DataFrame
sales_df = sales_df.append(forecast_df, ignore_index=True)
# Визуализация исходных данных и прогноза
plt.figure(figsize=(12, 6))
plt.plot(sales_df.index[:-12], sales_df['Продажи'][:-12], label='Исходные данные')
plt.plot(sales_df.index[-12:], sales_df['Прогноз продаж'][-12:], label='Прогноз')
plt.title('Прогноз продаж в магазине МВидео')
plt.xlabel('Дата')
plt.ylabel('Продажи')
plt.legend()
plt.grid(True)
plt.show()
На графике показаны исходные данные о продажах и прогноз продаж на следующие 12 месяцев. Этот пример демонстрирует, как использовать анализ временных рядов для прогнозирования будущих продаж в магазине электроники.
Заключение
В данной статье мы рассмотрели основные концепции и методы работы с временными рядами в Python. Мы изучили, как импортировать данные временных рядов, визуализировать их, а также провели анализ стационарности и сезонности.
В следующей части нашей серии статей, мы погрузимся в более продвинутые аспекты работы с временными рядами. Мы рассмотрим, как использовать модели прогнозирования временных рядов, чтобы, например, прогнозировать погоду с учетом исторических данных. Мы также углубимся в анализ временных рядов с переменными интервалами, что может быть полезно в различных прикладных областях. Кроме того, мы уделим внимание совместным временным рядам, где мы сможем исследовать взаимосвязи между разными временными рядами и принимать более информированные решения.
