Простое суффиксное дерево
Суффиксное дерево — мощная структура, позволяющая неожиданно эффективно решать мириады сложных поисковых задач на неструктурированных массивах данных. К сожалению, известные алгоритмы построения суффиксного дерева (главным образом алгоритм, предложенный Эско Укконеном (Esko Ukkonen)) достаточно сложны для понимания и трудоёмки в реализации. Лишь относительно недавно, в 2011 году, стараниями Дэни Бреслауэра (Dany Breslauer) и Джузеппе Италиано (Giuseppe Italiano) был придуман сравнительно несложный метод построения, который фактически является упрощённым вариантом алгоритма Питера Вейнера (Peter Weiner) — человека, придумавшего суффиксные деревья в 1973 году. Если вы не знаете, что такое суффиксное дерево или всегда его боялись, то это ваш шанс изучить его и заодно овладеть относительно простым способом построения.Прежде чем переходить к описанию суффиксного дерева, определимся с терминологией. Входные данные для алгоритма — это строка s, состоящая из n символов s[0], s[1], …, s[n-1]. Каждый символ — это байт. Хотя, конечно, всё описываемое здесь будет работать и для любых других последовательностей: битов, двухбайтовых символов юникода, двухбитовых символов последовательностей ДНК и так далее. Дополнительно будем полагать, что s[n-1] равен символу 0, который нигде более в s не встречается. Это последнее ограничение служит лишь для упрощения повествования и от него, на самом деле, достаточно просто избавиться. Строки вида s[i…j] = s[i]s[i+1]…s[j], где i и j — некоторые целые числа, называются, как обычно, подстроками. Подстроки вида s[i…n-1], где i — некоторое целое, называются суффиксами.Итак, главный герой. Суффиксное дерево для строки s — это минимальное по числу вершин дерево, каждое ребро которого помечено непустой подстрокой s таким образом, что каждый суффикс s[i…n-1] может быть прочитан на пути из корня до какого-нибудь листа и, наоборот, каждая строка, прочитанная на пути из корня до какого-нибудь листа, является суффиксом s. Проще всего разобраться с этим определением на пример (не обращайте внимания, пока что, на pos, len и to):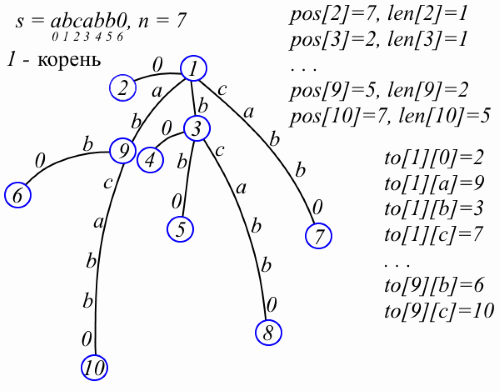 
Поскольку s[n-1] — это особый символ, в суффиксном дереве ровно n листьев, а значит O (n) вершин. Вершины мы будем нумеровать целыми числами. Метка на ребре из вершины v в отца v хранится в виде пары чисел: длина метки len[v] и позиция pos[v] сразу после этой метки в s, т.е. если метка — это строка t, то t = s[pos[v]-len[v]…pos[v]-1]. Пусть некоторая вершина v имеет k детей и t1, t2, …, tk — это метки на рёбрах от v к детям. Заметьте, что первые символы строк t1, t2, …, tk попарно различны, а значит ссылки на детей v можно хранить в мапе to[v], отображающем первый символ метки в соответствующего отпрыска. Я буду избегать объектно-ориентированного подхода в описании структур, чтобы сделать код короче и чтобы вы подумали «ух ты, какой компактный код». Итак, суффиксное дерево представлено следующим образом (теперь можно обратить внимание на pos, len, и to на рисунке выше):
int sz; //количество вершин в дереве
int pos[0…sz-1], len[0…sz-1], par[0…sz-1]; //par[v] — отец вершины v
std: map
Примеры использования суффиксного дерева
Чтобы освоиться с суффиксным деревом и одновременно понять, как его использовать, рассмотрим несколько примеров.Поиск подстроки в s
Возможно, самое первое что приходит в голову — это использовать суффиксное дерево для поиска подстрок. Довольно просто заметить, что строка u является подстрокой строки s тогда и только тогда, когда u можно прочитаться из корня суффиксного дерева (т.к. u = s[i…j] для некоторых i и j и поэтому суффикс s[i…n-1] начинается с u).Количество различных подстрок в строке s
Теми же рассуждениями можно установить, что каждая подстрока s соответствует некоторой позиции на метке какого-то ребра суффиксного дерева. Значит число различных подстрок — это число таких позиций и оно равно сумме len[v] по всем вершинам v кроме корня.Сжатие данных LZ77
Пример посложнее. Идея сжатия LZ77 (гуглите Lempel, Ziv) проста и может быть описано таким псевдокодом:
for (int i = 0; i < n; i = j+1) //сжимаем строку s[0..n-1]
if (символ s[i] не встречался ещё в s[0..i-1]) {
j = i, записать в выходной файл символ s[i]; //точный формат записи зависит от реализации
} else {
j = max{j для которого найдётся d < i такое, что s[i..j] = s[d..d+j-i]};
d = позиция 0,1,…,i-1 такая, что s[d..d+j-i] = s[i..j];
записать в выходной файл пару чисел (j-i+1, i-d) //точный формат записи зависит от реализации
}
}
Например, строка "aababababaaab” будет закодирована как "a(1,1)b(7,2)(3,10)” (обратите внимание на "перекрытие” строк abababa). Конечно, детали реализации могут сильно отличаться, но основная идея используется во многих алгоритмах сжатия. С помощью суффиксного дерева можно сжать s подобным образом за O(n). Для этого мы дополняем каждую вершину v нашего дерева полем start[v] таким, что start[v] равно наименьшему p при котором s[p..p+|str(v)|-1] = str(v), где |str(v)| – это длина str(v). Ясно, что для листьев это значение легко вычисляется. Для остальных вершин поле start вычисляется одним обходом дерева в глубину, т.к. start[v] = min{start[v1], start[v2], …, start[vk]}, где v1, v2, …, vk – дети v. Теперь, чтобы вычислить очередное значение j в нашем алгоритме сжатия, достаточно читать строку s[i..n-1] из корня до тех пор, пока текущая вершина v в дереве имеет start[v] Построение суффиксного дерева
Заранее предупрежу, что несмотря на то, что упрощённый алгоритм Вейнера проще, чем алгоритм Укконена и классический алгоритм Вейнера, он, тем не менее, по-прежнему является нетривиальным алгоритмом, и чтобы понять его, необходимо приложить некоторые усилия.Общий план. Префиксные ссылки
Алгоритм стартует с пустого дерева и последовательно добавляет суффиксы s[n-1..n-1], s[n-2..n-1], …, s[0..n-1]:
for (int i = n-1; i >= 0; i--)
extend (i); //добавить в дерево суффикс s[i…n-1]
Таким образом на k-й итерации цикла мы имеем суффиксное дерево для строки s[n-k+1…n-1] и добавляем в дерево суффикс s[n-k…n-1]. Ясно, что добавление нового самого длинного суффикса требует вставки одного нового листа и, возможно, одной новой вершины, «разбивающей» старое ребро. Основная проблема — найти позицию в дереве, где будет присоединён новый лист. Для решения этой проблемы суффиксное дерево дополняется префиксными ссылками.С каждой вершиной v мы ассоциируем префиксные ссылки link[v] — мап, отображающий символы в номера вершин следующим образом: для символа a link[v][a] определено тогда и только тогда, когда в дереве существует вершина w такая, что str (w) = a str (v) и в этом случае link[v][a] = w. (Если вы были знакомы с классическим алгоритмом Вейнера, то заметили, что наши префиксные ссылки соответствуют «явным» классическим префиксным ссылкам, а «неявные», оказывается, вообще не требуются; если же вы были знакомы с алгоритмом Укконена, то могли заметить, что префиксные ссылки — это обращённые «суффиксные ссылки».) На рисунке префиксные ссылки обозначены красным, а в прямоугольниках написаны символы, соответствующие ссылкам (смысл фиктивной вершины 0 смотрите ниже).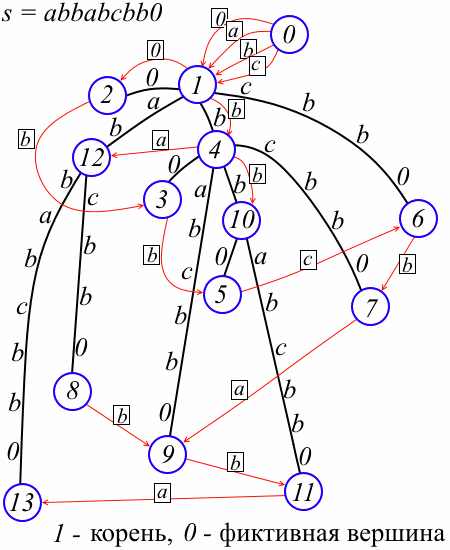
Таким образом мы имеем дополнительную структуру:
std: map
Алгоритм
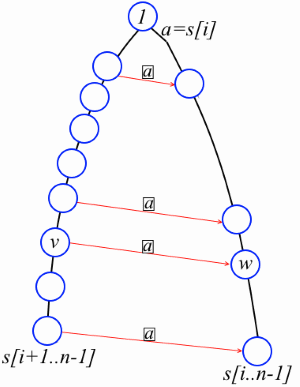Лемма. Пусть i — некоторое число от 0 до n-2. Рассмотрим суффиксное дерево строки s[k…n-1], где k <= i. Если w – некорневая вершина на пути от корня к листу, соответствующему s[i..n-1], то на пути от корня к листу, соответствующему s[i+1..n-1], есть вершина v такая, что s[i]str(v) = str(w) и link[v][s[i]] = w (смотрите рисунок).Докажем это. Обозначим str(w) = s[i]t. По определению суффиксного дерева либо w — лист, либо у w есть как минимум два потомка. Если w — лист, то v — это лист, соответствующий строке s[i+1..n-1]. Пусть w не лист. Тогда найдутся некоторые различные символы a и b такие, что to[w][a] ведёт к одному ребёнку w, а to[w][b] к другому. Значит s[i]ta и s[i]tb – это подстроки s (как минимум одна из них начинается не в позиции i). Следовательно ta и tb – тоже подстроки и в дереве должна быть вершина v такая, что str(v) = t. Ясно, что v лежит на пути к листу, соответствующему s[i+1..n-1], и, по определению префиксных ссылок, имеем link[v][s[i]] = w.
Итак, положим мы имеем суффиксное дерево для строки s[i+1…n-1] и собираемся добавить лист для строки s[i…n-1] и сообразно этому обновить префиксные ссылки. Смотрите рисунок ниже. Обозначим через old лист, соответствующий s[i+1…n-1]. Место «стыковки» нового листа — это вершина w», которая, возможно, ещё не создана. Через w обозначена вершина, лежащая непосредственно над w» (если w» уже есть в дереве, то w = w» и в этом случае достаточно только добавить новый лист). Для простоты рассмотрим сначала случай, когда w не корень. По лемме найдётся вершина v на пути от old до корня такая, что link[v][s[i]] = w.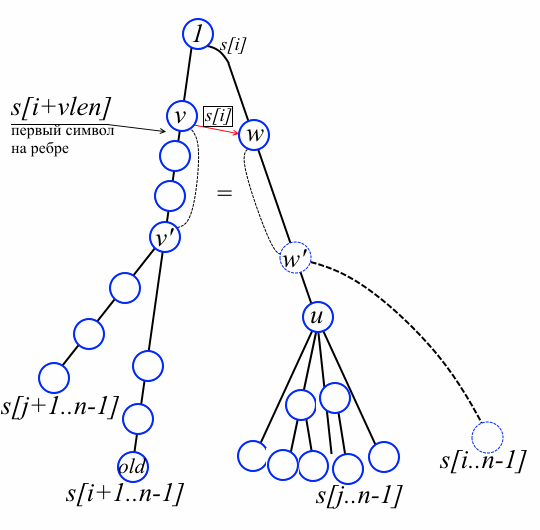
Факт 1. На пути от v к old нет вершин v» таких, что link[v»][s[i]] определено. Пусть, от противного, v» — такая вершина. Тогда вершина link[v»][s[i]] — предок w» и, одновременно, потомок w (по определению префиксных ссылок). Но мы выбрали w как ближайшую вершину от места стыковки! Противоречие.
Наш алгоритм первым делом находит v и w. Заодно мы вычисляем в переменной vlen значение |str (v)|+1 и складываем в стэк path все пройденные вершины — они ещё пригодятся. Заметьте, что по окончании цикла s[i+vlen] равно первому символу на ребре от v к отпрыску v на пути к old (см. рисунок выше).
int v, vlen = n — i, old = sz — 1;//в нашей реализации old — это последняя вершина for (v = old; ! link[v].count (s[i]); v = par[v]) { vlen -= len[v]; path.push (v); } int w = link[v][s[i]]; Факт 2. Вершина w» уже присутствует в дереве тогда и только тогда, когда to[w][s[i+vlen]] не определено; в этом случае w = w». Если немного помедитировать над рисунком выше и замечанием о значении символа s[i+vlen], это утверждение становится очевидным.Факт 3. На пути от v до old есть вершина v» такая, что s[i]str (v») = str (w»), даже если w» ещё не существует. Если w» уже есть в дереве, то утверждение очевидно по факту 2 и v» = v. Предположим w» ещё только предстоит создать. Обозначим u = to[w][s[i+vlen]]. Выберем произвольный лист из поддерева с корнем u; пусть этот лист соответствует суффиксу s[j…n-1] для некоторого j. Ещё не вставленный суффикс s[i…n-1] и суффикс s[j…n-1] расходятся в «неявной» вершине w». А вот листья, соответствующие s[j+1…n-1] и s[i+1…n-1], уже представлены в дереве и расходятся в некоторой вершине v». Ясно, что s[i]str (v») = str (w»), а значит v» лежит на пути от v к old. На этом месте стоит в последний раз вглядеться в рисунок выше. Мы приступаем к основной части алгоритма.
Теперь, когда мы нашли w, наша задача найти место стыковки нового листа, т.е. фактически мы ищем len[w»] и вершину v». В случае w = w» достаточно присоединить лист к w и провести префиксную ссылку из old в этот лист. Рассмотрим сложный случай, когда w!= w», т.е. есть ребро из w по символу s[i+vlen]. Обозначим, опять, u = to[w][s[i+vlen]]. Мы последовательно достаём из стэка path вершины пока не найдём вершину v» такую, что s[i]str (v») = str (w»). Как мы определяем, что нашли нужную вершину? Пусть v1, v2, …, vk — верхние вершины из стэка path причём vk = v» (смотрите рисунок ниже). Через ap обозначим первый символ на ребре, следующем из vp к потомку vp на пути к old. Определим a0=s[i+vlen]. Пусть t — метка на ребре от w до u. Символ t[len[v1] + len[v2] + … + len[vp-1]] будем называть символом, соответствующим ap на t. Так как w» — это точка ответвления суффикса s[i…n-1] на ребре от w к u, символ ak не равен соответствующему символу на t. С другой стороны, по той же причине для каждого p=0,1, …, k-1 символ ap равен соответствующему символу на t. С рисунком это рассуждение станет понятнее:
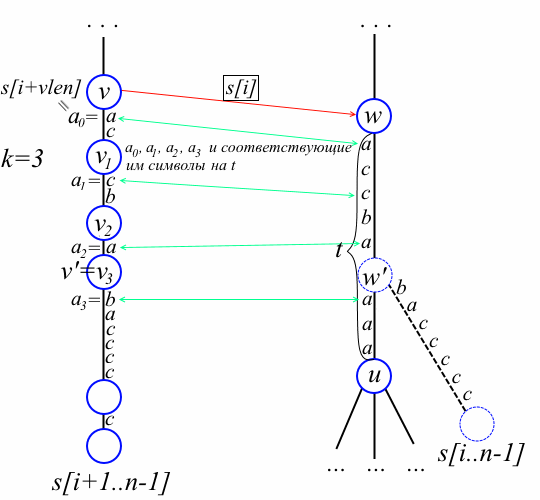
Полученное замечание является ядром упрощённого алгоритма Вейнера. Интересно, что нам достаточно сравнивать только первый символ на рёбрах с соответствующим символом на t, а не все символы. По-существу это простое наблюдение — это то, что заметили Бреслауэр и Италиано, а раньше почему-то никто не замечал. Осталось не забыть провести префиксную ссылку из v' в w' и префиксную ссылку из old в новый лист. Итак, алгоритм вставляет новый суффикс s[i…n-1] следующим образом:
if (to[w].count (s[i + vlen])) { //если w!= w» int u = to[w][s[i + vlen]]; //sz — это новая вершина w», которую мы создаём //т.к. w!=w', условие s[pos[u] — len[u]] == s[i + vlen] на первой итерации цикла истинно for (pos[sz] = pos[u] — len[u]; s[pos[sz]] == s[i + vlen]; pos[sz] += len[v]) { v = path.top (); path.pop (); //очередной кандидат на v» vlen += len[v]; } Разбить ребро от w к u вершиной w»=sz; len[w»] = len[u]-(pos[u]-pos[sz]) link[v][s[i]] = sz; //суффиксная ссылка из v» в w» w = sz++; //устанавливаем w = w» для вставки нового листа } //в этой точке переменная w содержит w' link[old][s[i]] = sz; //суффиксная ссылка из old в новый лист sz Присоединить лист sz к w; len[sz] = n — (i + vlen) pos[sz++] = n; //pos для листьев всегда равен n Осталось рассмотреть частный случай, когда w — это корень. Эта ситуация полностью аналогична, но некоторые значения сдвинуты на единицу. Можно было бы, конечно, обработать этот случай отдельно, но с помощью фиктивной вершины сделать это проще и дополнительного кода писать не придётся. В этом месте важную роль играет тот факт, что par[1]=0, len[1]=1 и link[0][a]=1 для всех символов a. Таким образом цикл поиска вершины v обязательно оборвётся на вершине 0, а значение len[1]=1 обеспечит необходимый сдвиг на единицу. Разобраться в подробностях не составит труда и я оставлю это как упражнение. Надеюсь тайный смысл фиктивной вершины на этом должен проясниться. Объединяя всё вместе, получаем такое решение: void attach (int child, int parent, char c, int child_len) //вспомогательный метод { to[parent][c] = child; len[child] = child_len; par[child] = parent; } void extend (int i) //один шаг алгоритма; вызывать для i=n-1, n-2,…,0 { int v, vlen = n — i, old = sz — 1; for (v = old; ! link[v].count (s[i]); v = par[v]) { vlen -= len[v]; path.push (v); } //по окончании цикла vlen = |str (v)|+1 int w = link[v][s[i]]; if (to[w].count (s[i + vlen])) { //если w!= w» int u = to[w][s[i + vlen]]; for (pos[sz] = pos[u]-len[u]; s[pos[sz]]==s[i + vlen]; pos[sz] += len[v]) { v = path.top (); path.pop (); //очередной кандидат на v' vlen += len[v]; } attach (sz, w, s[pos[u] — len[u]], len[u] — (pos[u] — pos[sz])); //присоединить w'(=sz) к w attach (u, sz, s[pos[sz]], pos[u] — pos[sz]); //присоединить u к w'(=sz) w = link[v][s[i]] = sz++; //провести префиксную ссылку из v' в w'; установить w = w' для вставки нового листа } //в этой точке переменная w содержит вершину w' link[old][s[i]] = sz; //префиксная ссылка из старого листа к новому attach (sz, w, s[i + vlen], n — (i + vlen)); //присоединить новый лист sz к вершине w' pos[sz++] = n; //pos для листьев всегда равен n } void init () { len[1] = 1; pos[1] = -1; par[1] = 0; //важно, что par[1] = 0 и len[1] = 1 (!) for (int c = 0; c < 256; c++) link[0][c] = 1;//из вершины 0 префиксные ссылки по всем символам ведут в корень } Оценка времени работы алгоритма В заключении поймём почему вся описанная конструкция выполняет O(n) операций. Высотой вершины v назовём количество вершин на пути от корня к v. Напомню, что шаг алгоритма – это добавление нового суффикса в дерево. Обозначим через hi высоту вершины, соответствующей самому длинному суффиксу на i-м шаге. Пусть ki – это число вершин, пройденных от old к v на i-м шаге. Как изменяется значение hi? Если ещё раз взглянуть на рисунок к лемме, поразмыслив, вы заметите, что hii-1 – ki-1 + 2. Число операций, выполненных на i-м шаге, пропорционально ki, а значит, как мы только что заметили, O(hi+1 – hi + 2). Отсюда очевидно, что алгоритм выполняет O(2n + (h1 – h2) + (h2 – h3) + … + (hn-1 — hn)) = O(n) операций в сумме.Небольшое оптимизационное замечание. Учитывая время доступа к мапам, время работы алгоритма Вейнера (так же как и Укконена) – O(n log m), где m – число различных символов в строке. Когда алфавит очень мал, вместо мапов лучше использовать массивы, чтобы сделать Вейнера действительно линейным.
Справедливости ради стоит отметить, что упрощённый алгоритм Вейнера (а классический и подавно) потребляет примерно в полтора-два раза больше памяти, чем Укконен. Также тесты показали, что упрощённый Вейнер работает примерно в 1.2 раза медленнее (тут он несильно уступает Укконену). Тем не менее все эти недостатки отчасти компенсируются простотой реализации Вейнера и отсутствием большого числа подводных камней.
Ссылки в хронологическом порядке P. Weiner. «Linear pattern matching algorithms» 1973 — первая статья Вейнера, в которой введено суффиксное дерево и дан линейный алгоритм.E. McCreight. «A space economical suffix tree construction algorithm» 1976 — более легковесный алгоритм построения суффиксного дерева.
E. Ukkonen. «On-line construction of suffix trees» 1995 — модификация алгоритма МакКрейта; самый популярный современный алгоритм.
D. Breslauer, G. Italiano. «Near real-time suffix tree construction via the fringe marked ancestor problem» 2013 (предварительная версия в 2011) — описание упрощённого алгоритма Вейнера в этой статье занимает один абзац (remark на 10й странице), а всё остальное посвящено другой близкой проблеме.
P.S. Спасибо Мише Рубинчику и Олегу Меркурьеву за помощь в тестировании алгоритма и предложения по улучшению кода.
