Proof-of-Proof-of-Work на пальцах. На пути к разумному блокчейну
Блокчейн-протоколы должны обеспечивать консенсус среди нод децентрализованной системы. Пожалуй, самым известным алгоритмом консенсуса можно считать «тормозунутый, но надежный, потому что тормознутый» алгоритм Proof-of-Work: каждая нода, имея набор новых транзакций перебирает некоторое число nonce, являющееся полем блока. Блок считается валидным, если валидны все транзакции внутри него и хэш-функция от заголовка блока имеет некоторую общепринятую особенность (например, количество нулей в начале, как в Bitcoin):
Hash( Block{transaction,nonce,…} ) = 000001001...
Как известно, блокчейн — это цепочка блоков. Цепочкой он является потому, что внутри каждого блока записан id (как правило хэш от заголовка) предыдущего блока. Для последующих рассуждений блокчейн в упрощенном виде можно представить так:

В процессе синхронизации ноды с другими нодами, ей необходимо осуществить валидацию всех блоков, которые ей прислали соседи — проверить хэши и транзакции всех новых блоков, а в случае первого подлючения, до самого первого блока (genesis -block). Нетрудно предположить, что это достаточно длительный и затратный процесс…
Есть вариант запросить у соседних нод несколько последних блоков и, доверившись, принять их как валидные. Но этот вариант не соответствует духу безопасности в «среде, где никто никому не доверяет»
PoPoW-ноды.
Хэш-функция от заголовка блока является его id. Как было сказано ранее, в сети Bitcoin, как и во многих других сетях, особенностью, по которой определяется валидность блока, является число нулей в начале записи id. Это известное и общее для всех майнеров число нулей, называют сложностью майнинга T (mining target). Валидный хэш с T нулями в начале может иметь больше нулей в начале, чем Т. Конкретнее, половина блоков будет иметь только T нулей в начале; половина блоков будет иметь T+1 нуль в начале; четверть блоков T+2 нулей и.т.д. Например так может выглядеть набор валидных блоков для T = 5:
000000101… (6 нулей)
000001110… (5 нулей)
000001111… (5 нулей)
000000010… (7 нулей)
000000101… (6 нулей)
000001110… (5 нулей)
000001111… (5 нулей)
Количество нулей, превышающее T в id блока назовем уровнем µ, а блоки с уровнем µ будем называть µ — суперблоками. Если блок является µ — суперблоком, то он так же является и
(µ -1)-суперблоком. Таким образом, пока ничего не изменяя, а лишь оперируя введенным параметром µ, можем представить цепочку блоков в следующем µ-уровневом виде:
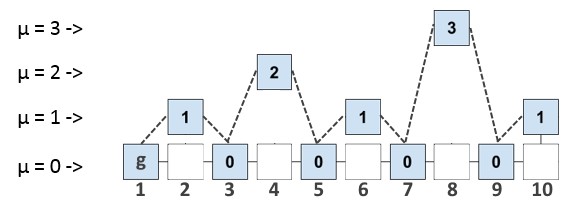
Блоки пронумерованы для простоты описания, нумерация не несет смысловой нагрузки.
Теперь подумаем, как мы можем это использовать. Если в заголовок каждого блока записывать не только id предыдущего блока, но и id всех последних блоков на каждом уровне, то мы позволяем каждому блоку ссылаться на более «древние» блоки, чем предыдущий. Набор всех последних на каждом уровне блоков будем называть interlink (множественная ссылка). Например, Interlink для блока 8 выглядит так: 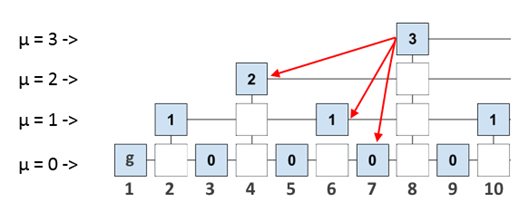
Что нам это дает? Допустим, мы подключили новую ноду и теперь хотим безопасно синхронизировать её. Как мы уже сказали, для полноценной валидации нового блока, ноде нужно «прошагать» до genesis — блока по всему блокчейну. Однако, если мы будем иметь в валидируемом блоке ссылки на некоторые «опорные» блоки, то сможем «прошагать» до genesis — блока, запросив у других нод не весь блокчейн, а лишь некоторое доказательство (proof), которое будет содержать короткий маршрут до самого первого блока. Сам маршрут будет являться валидной подцепочкой самого блокчейна, так как блоки подцепочки последовательно ссылаются друг на друга. 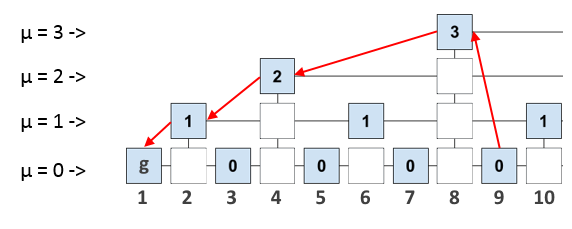
Доказательство — это набор заголовков нескольких предыдущих блоков. Строго говоря, доказательство содержит не только «короткий маршрут», но и ещё несколько заголовков других блоков. Это сделано для верификации доказательства (verify) по задаваемым параметрам безопасности m, k и др. (подробное описание приводится в оригинальной статье, ссылка в конце).
Нода, которая не хранит весь блокчейн, а лишь запрашивает proof у full-нод, хранящих всю историю, называется PoPoW — нодой. Теоретически такую ноду можно развернуть на маломощном компьютере, смартфоне.
Алгорим работы PoPoW-протокола следующий:
1. PoPoW-нода запрашивает доказательство для блока у full — ноды.
2. Full — нода (proover) формирует доказательство и отправляет его.
3. PoPoW-нода (verifier) проверяет доказательство, сопоставляет с доказательствами других нод и делает заключение о валидности блока.
Также стоит отметить, что сложность создания PoPoW доказательства не уступает сложности создания полной цепочки из валидных заголовков (хэш функция заголовка содержит Interlink, поэтому «подделывать» блоки нечестной ноде пришлось бы с учетом µ-уровневой иерархичности). Поэтому использование для валидации блока PoPoW доказательства не влечет потери безопасности.
NiPoWPoW — алгоритм
Алгорим NiPoPoW — Non-Interactive Proof-of-Proof-of-Work — включает в себя усовершенствованные формирование и проверку доказательств, он устойчив к некоторым атакам, которым подвержен PoPoW. Ссылка на оригинальную статью от авторов так же в конце.
Для чего все это нужно?
С помощью этих алгоритмов решаются две актуальные проблемы: эффективная верификация транзакции и эффективное доказательство для сайдчейнов (Sidechains).
В первом случае этот алгоритм позволяет подключать к сети «легкие» ноды, которые смогут быстро синхронизироваться с сетью.
Во втором случае алгоритм позволяет хранить и ссылаться на события, произошедшие в других блокчейн-сетях, что полезно для клиентов и кошельков, работающих с несколькими блокчейнами. PoPoW-доказательство достаточно короткое для того, чтобы можно было поместить его в транзакцию. Например, можно писать смарт-контракты в блокчейне A, которые опираются на какие-то события в блокчейне Б.
Данный обзор составлен на свежую голову после участия в хакатоне Unblock Hackathon, где одним из заданий было реализовать данный протокол. Авторами задания были партнеры хакатона из Ergo platform, внутри которой используется этот алгоритм.
Текст подготовлен на основе оригинальных статей
PoPoW: Proofs of Proofs of Work with Sublinear Complexity. Aggelos Kiayias, Nikolaos Lamprou, and Aikaterini-Panagiota Stouka
NiPoPoW: Non-Interactive Proofs of Proof-of-Work. Aggelos Kiayias, Andrew Miller and Dionysis Zindros
