Производная с вещественным показателем
Этой идеей со мной поделился однокурсник по физфаку Харьковского университета Витька Середницкий на одной из общажных посиделок (читай — попоек). Были мы молоды, усердно грызли гранит науки, всерьез думали, что будем всю жизнь заниматься теоретической физикой, да и время для мечтаний на дворе было подходящее — год примерно 1989. Идея оказалась не нова, но поисследовать ее я загорелся, и вот что получилось.
Функция с достаточно хорошим поведением (я опускаю здесь математические тонкости) может быть представлена в виде ряда Фурье, разложения по синусам и косинусам:

(мы берем, для упрощения, интервал [–π, π ], чтобы не выписывать добавочные коэффициенты вида π /l)
Поскольку синусы и косинусы — функции периодические, то разложенная функция также превращается в периодическую. Для функции y = x на всей числовой оси ее график будет выглядеть вот так, кусочно:

Можно расширить диапазон с [–π, π] до любого [–l, l], и даже, устремив l к бесконечности, превратить ряд в интеграл, чтобы разложение стало применимым для всей числовой оси. Этим мы не будем заниматься, для цели нашей статьи это несущественно.
Коэффициенты ряда Фурье определяются по формулам, n = 0, 1, 2, 3 …
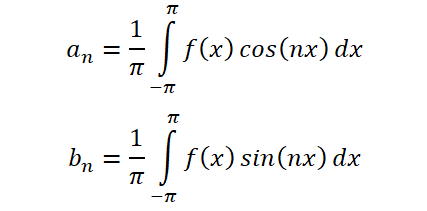
Далее, ряд, при неких условиях его сходимости, может быть продифференцирован почленно, тогда получим для первой производной

Витя заметил, что превращение синуса в косинус и наоборот эквивалентно сдвигу на π/2, и тогда последнюю формулу можно записать в виде:

Ну и теперь остается только постулировать для производной с вещественным показателем α

«нулевая» производная будет совпадать с самой исходной функцией, при α = 1 получим обычную первую производную.
(Производные — я встречал такое обозначение — записывают как степень в скобочках, если не пользоваться «единичной системой счисления» с нужным количеством штрихов. Правда, в этом случае показатель производной почему-то обозначался римской цифрой! Как писать римскими цифрами вещественные числа я просто не представляю).
Исследуем это определение.
Во-первых, интересно, влияет ли порядок дифференцирования на результат. Возьмем последовательно производную с показателем альфа и затем с показателем бета. Процедуру вычислений — там достаточно несложные алгебраические преобразования — уберем под кат, результат положительный:
 Под катом
Под катом
Раскроем косинус и синус суммы в формуле для производной порядка альфа, перегруппируем слагаемые и приведем к виду обычного разложения Фурье
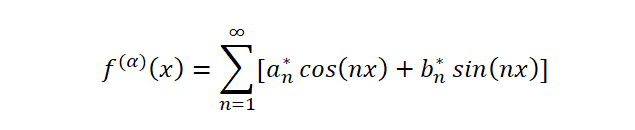
Где

Теперь снова применим формулу для производной порядка β

Если теперь подставить сюда выражения для a*n и b*n, а затем свернуть обратно полученные члены в косинус и синус суммы углов, получим окончательно

Теперь коснемся сходимости. Обычная сходимость ряда в каждой точке сомнений не вызывает. Вопрос состоит в равномерной сходимости. Удивительное дело — ее мне удалось доказать только для четных функций (симметричных относительно оси Y), в противном случае, похоже, она и не имеет место быть, чуть позже мы увидим этому косвенное подтверждение.
Интересно, что понятие равномерной сходимости появилось (ну или было осознано) достаточно поздно. Вообще нужно сказать, что окончательно все тонкие вопросы матанализа были прояснены и долизаны только к середине XIX века, почти через 200 лет после создания его самого гениями Ньютоном и Лейбницем. В части равномерной сходимости эта заслуга принадлежит Карлу Вейерштрассу (статья в Википедии, лучше смотреть более полный английский вариант).
Ну и, наконец, перейдем к графикам.
Брюки превращаются… Превращаются брюки…
Простейшая линейная функция не без сложностей переходит в константу:
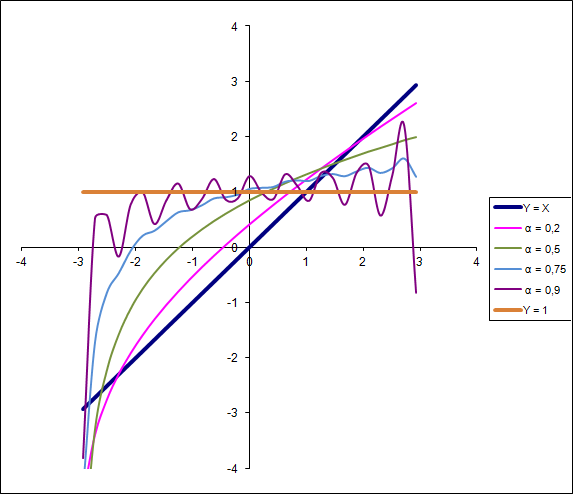
Парабола гладко переходит в линейную функцию:

Кубическая парабола становится квадратичной

График получился сильно загроможденным, развернем:
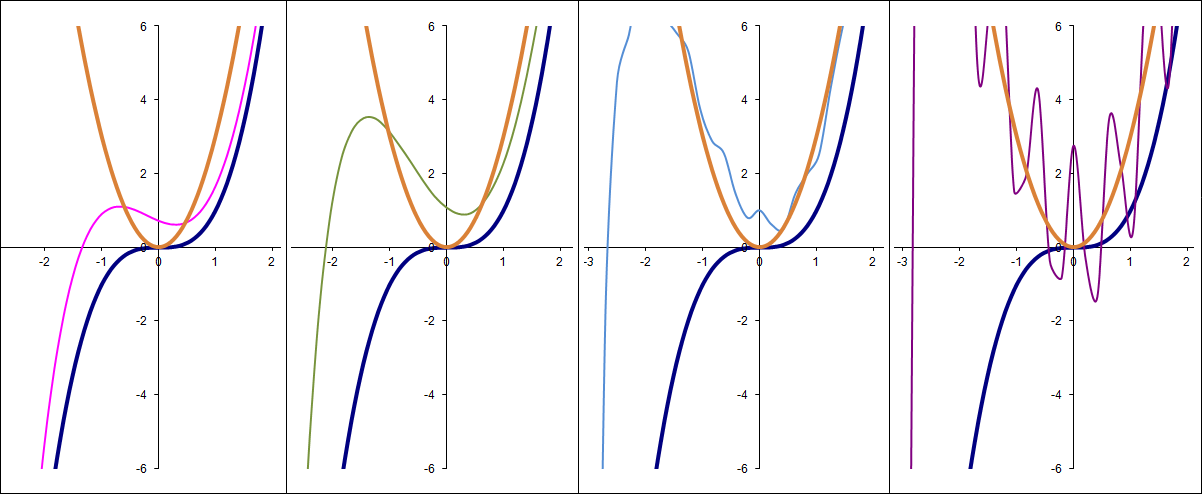
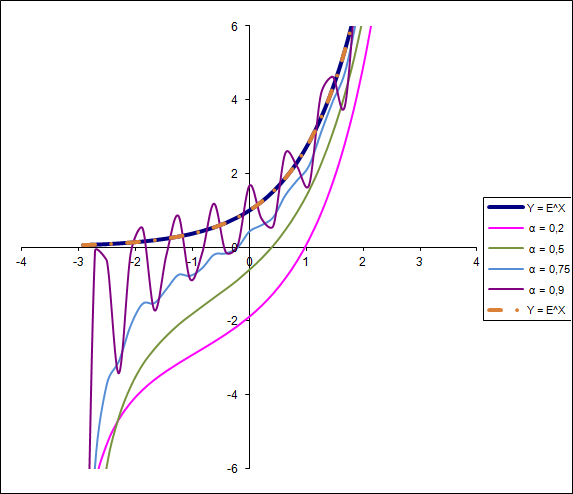
Экспонента после некоторых колебаний вновь сливается сама с собой:
Гиперболический косинус становится гиперболическим синусом

(Кстати, как у вас коротко называли гиперболические функции? У нас — «шинус» и «чосинус»)
Видно, что у четных функций (x2, ch (x)) сходимость идет гладко, а нечетных — с биениями, что подтверждает тезис об отсутствии равномерной сходимости в общем случае. Заметим тут, что гиперболический косинус («чосинус») есть не что иное, как выделение из экспоненты ее четной части — по известной формуле разбиения любой функции на четную и нечетную:
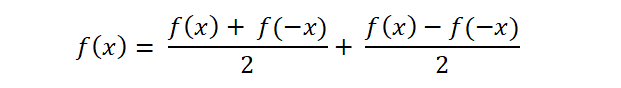
— и сразу получаем для четной части равномерную сходимость (хотя бы «на глаз»).
Обидно, что не все элементарные функции позволяют получить формулу коэффициентов Фурье в аналитическом виде — ни для натурального логарифма, ни для функции типа 1/x это не получается. Можно было бы, конечно, насчитать их программно, но мне показалось, что приведенных примеров вполне достаточно, качественная картинка примерно одна и та же для разных функций.
Ортогональные системы функций
Немного о разложении функций в ряды. Удивительное дело, но простейшее, элементарное разложение вектора на плоскости по двум направляющим вдоль осей X и Y может быть далеко обобщено и на случай функций. Пусть у нас есть обычное векторное пространство R2 с операциями сложения векторов и умножения вектора на число. Разложение вектора в обычном декартовом пространстве может быть также введено через понятие скалярного произведения.
Для векторов a = (ax, ay) b = (bx, by) их скалярное произведение определяется как
Если произведение равно нулю, вектора являются ортогональными. В других случаях получаем проекцию одного вектора на направление другого. Скалярное произведение вектора на самого себя дает просто квадрат его длины — по теореме Пифагора
<a, a> = ax2 + ay2
Рассмотрим 2 вектора (орта) вида nx = (1,0) и ny = (0,1). Они ортогональны <nx, ny> = 0 и нормированы на единицу <nx, nx> = <ny, ny> = 1
Произведение орта на любой вектор есть проекция вектора на соответствующую ось:
<a, nx>=ax <a, ny>=ay
И любой вектор в R2 представим как
a = <a, nx>nx + <a, ny>ny,
то есть вектора nx и ny образуют базис.
Пространство функций также можно объявить линейным векторным пространством. И если мы придумаем в этом пространстве скалярное произведение, то все вышеприведенные соображения и выводы можно смело переносить сюда — хотя в этом случае совершенно неочевидно, что можно понимать, например, под «квадратом длины функции», «углом между двумя функциями» или же «ортогональностью двух функций друг другу». Последнее просто означает равенство нулю их скалярного произведения.
Скалярное произведение в пространстве функций можно ввести следующим образом:

А векторами такого пространства (его называют L2) объявим все функции, для которых такой интеграл на любом ограниченном интервале конечен (то есть любая функция имеет конкретную конечную «длину», что бы это ни значило). Тогда и скалярное произведение двух любых функций из L2 — конечно (по неравенству Коши-Буняковского-Шварца).
И, как оказывается, в этом пространстве существует бесконечный базис из взаимно ортогональных функций вида sin (nx), cos (nx), поскольку

И то же самое для произведения синусов, а для произведения синуса на косинус всегда будет ноль.
Теперь сразу становится понятным, откуда взялись формулы для коэффициентов an, bn в начале статьи (это просто «проекции» функции на соответствующий вектор из базиса, чбэнз), и сам ряд Фурье.
(мы не касаемся тут вопросов сходимости подобных бесконечных разложений вообще, сходимости именно к нашей функции, а также других тонких вопросов, а излагаем только идейную часть)
Оказывается, что синусы и косинусы — не единственно возможный базис в пространстве функций! Существуют и другие системы ортогональных функций — например, многочлены Лежандра. Что интересно, к этим многочленам приводит процесс ортогонализации Грамма-Шмидта для обычного ряда степенных функций — 1, x, x2, x3). И разложение в ряд Тейлора, в который, как мы знаем, разлагаются все бесконечно дифференцируемые функции, можно перевести в разложение по многочленам Лежандра. Подробности тут.
Рассуждения нематематика.
Давайте попробуем такой ход рассуждений. Если свойство какого-нибудь математического объекта выражается, к примеру, натуральным числом, то почему бы не представить, что могут существовать объекты, у которых это свойство целое (то есть может быть нулем или отрицательным), дробное (рациональное), вещественное и так далее? Главное, чтобы в уже известных ситуациях определение такого свойства совпадало с исходным, а дальше — простор для интерполяций. В конце концов, те же пифагорейцы считали, что сами числа могут быть только натуральными, остальное — от лукавого, и в результате понятие действительного числа и континуума задержалось с появлением до самого конца XIX века.
Едва ли математические открытия совершаются таким «механическим» путем. Однако можно навскидку назвать несколько областей, где по факту и случилось такое обобщение:
— степень с вещественным показателем — через натуральные логарифмы,
— комплексные числа («кто сказал, что нельзя извлекать корни из отрицательных чисел»?),
— расстояния между точками псевдоевклидова пространства, которые могут быть отрицательными — и удивительно, как это нашло применение в Специальной теории относительности,
— дробная размерность топологических пространств и всяких хитрых множеств
Ну и т.д. и т.п. Производная с вещественным показателем тоже хорошо ложится в этот ряд. А есть еще примеры? — напишите в комментах!
Привет, Андрей Птолемей!
Интересно, что система эпициклов и деферентов Птолемея, которая пыталась объяснить непонятные древним движения планет была, по сути, тем же разложением в ряд Фурье, может, в слегка искаженном виде. Наплоди мы достаточное количество таких окружностей, по которым вращаются вокруг Земли условные точки, а вокруг них — еще точки, центры других окружностей, можно было бы приблизиться к истинным движениям планет со сколь угодной точностью, и никакая система мира Коперника с Солнцем в центре нам не понадобилась бы!
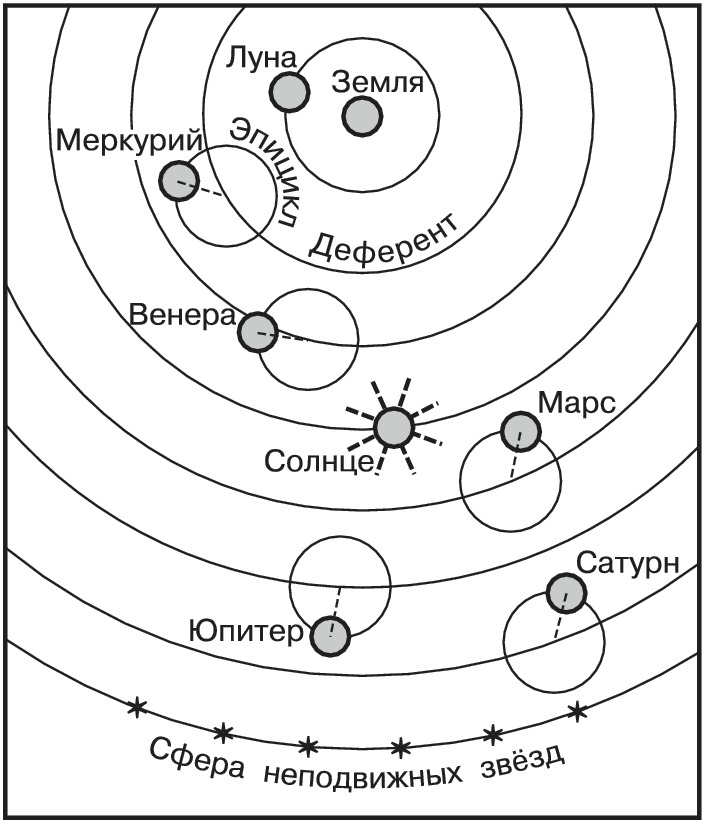
Источник картинки — БСЭ, Большая Советская Энциклопедия
Да, и вот собственно статья из Википедии на эту самую тему.
