Программная реализация шифровальной машины «Энигма» на языке Си
Введение
В своё время для преподавания, на промежутке между двумя предметами ОАиП (Основы алгоритмизации и программирования) и КСЗИ (Криптографические средства защиты информации) я реализовывал шифровальную машину «Энигма», чтобы показать как можно применять: 1) программирование для изучения криптографии; 2) криптографию для изучения программирования. В определённой мере, реализация классических шифров очень хорошо может прокачивать не только понимание внутреннего механизма работы того или другого алгоритм шифрования, но также и навыки самого программирования, потому как реализация любого шифра — это в первую очередь алгоритмическая задача.
В данной работе не будет исторического введения в понимание того, что представляет собой шифровальная машина «Энигма» в довоенное и в военное время, как она модифицировалась, а также как она взламывалась. На всё это существует большое количество написанных работ как на хабре, так и в книгах. Для людей, кому интересно всё вышеописанное я оставлю список литературы, с которым вы можете ознакомиться.
Механизмы шифрования
Шифровальная машина «Энигма» внешне выглядит как печатающая машинка, за исключением того факта, что шифруемые символы не печатаются автоматически на определённый лист бумаги, а указываются на панели посредством загорания лампочки.

Шифровальная машина «Энигма»
Шифровальная машина «Энигма» обладает тремя основными механизмами.
Роторы. Сердце всех шифровальных машин того времени. Со стороны классической криптографии они реализуют полиалфавитный алгоритм шифрования, а их определённо выстроенная позиция представляет собой один из основных ключей шифрования. Каждый ротор не эквивалентен другому ротору, потому как обладает своей специфичной настройкой. Военным на выбор давалось пять роторов, три из которых они вставляли в «Энигму». Выбор позиций, для вставки роторов, также играл свою роль, потому как образовывал свойство некоммутативности. Иными словами если существует настройка трёх роторов равная (A, B, C), то её замена на настройку (B, A, C) будет приводить к иному результату шифрования. Это говорит о том, что существовало (5!) / (2!) = 60 комбинаций выбора и подстановки. Далее, каждый ротор обладал 26-тью гранями, где каждая грань представляла собой нумерацию английского алфавита. Выбор одной определённой грани из 26-ти также представляло собой инициализацию ключа шифрования. Т.к. в сумме у нас находится три ротора, то всевозможных вариаций ключа будет существовать 26³ = 17 576. Итого, если учитывать все факторы выбора, подстановки и установки, то количество всевозможных ключей только на основе роторов будет равно ((5!) / (2!)) * (26³) = 60×17 576 = 1 054 560. Чисто технически, для того времени это количество комбинаций уже можно было эффективно взламывать, нанимая большое количество людей из третьего мира, выплачивая им копейки.

Открытая панель с роторами
Рефлектор (отражатель). Статичный механизм, позволяющий шифровальным машинам типа «Энигма» не вводить помимо операции шифрования дополнительную операцию расшифрования. Связано это с тем, что в терминологии классической криптографии рефлектор представляет собой просто частный случай моноалфавитного шифра — парный шифр, особенностью которого является инволютивность шифрования, где функция шифрования E становится равной функции расшифрования D, иными словами E = D. Это приводит к следующим выводам: если существует сообщение M, то справедливы становятся следующие утверждения D (E (M)) = E (E (M)) = M, E (E (E (M))) = E (M) = D (M). Парный шифр крайне примитивен в своей реализации, так допустим у нас существует в алфавите всего 4 символа {A, B, C, D}. Т.к. парный шифр — это разновидность моноалфавитного, то существует всегда и постоянно связь 1к1 для открытого и закрытого символов. Далее, если выбираем связь A=>B, то это говорит о том, что символ A должен зашифровываться символом B. Чтобы у нас появилась инволютивная связь, нам необходимо выбрать теперь символ B и привязать его к A, иными словами создать связь B=>A при шифровании. Вследствие этого применяем свойство транзитивности и получаем: если A=>B и B=>A, то A=B. Также делаем и с оставшимися символами C=D. Теперь дважды шифруя символ A, мы будем неявно применять композицию функций D*E, вследствие чего будем вновь получать символ A.
Принцип работы рефлектора — выстраивание парных символов
Коммутаторы. Своеобразный «множитель» возможных вариаций ключей шифрования. Представляет собой также как и рефлектор парный шифр, но в отличие от последнего является динамическим механизмом, то-есть редактируемым и сменяемым. Коммутаторы, можно их рассматривать как некие кабеля, вставляются в коммутационную панель, на которой изображены символы английского алфавита. Один коммутатор имеет два конца, каждый из которых вставляется в два отверстия коммутационной панели. Связь коммутатора с двумя отверствиями, над которыми изображены символы алфавита и представляет собой связь парного шифра между выбранными двумя символами. Так например, если коммутатор был вставлен в два отверстия (Q, D), то это говорит о том, что Q и D стали парными символами при шифровании. На одну шифровальную машину давалось десять коммутаторов, существовало 26 возможных отверстий в коммутационной панели (количество символов алфавита), один коммутатор одновременно связывал два символа такой панели, то-есть все коммутаторы затрагивают в общей сложности 20 отверстий. Всё это приводит к следующему количеству возможных расстановок коммутаторов на коммутационной панели (26!) / (6! * 10! * 210) = 150 738 274 937 250 [(постепенный_выбор_всех_букв_алфавита) / (оставшиеся_шесть_неиспользуемых_символов * двадцать_коммутаторов_как_десять_пар * все_десять_пар_коммутативны)].

Коммутационная панель
Итого, учитывая все вышеописанные механизмы, а точнее роторы и коммутаторы, можно вычислить количество всех возможных ключей, которое будет равно [((5!) / (2!)) * (26³)] * [(26!) / (6! * 10! * 210)] = 60×17 576×150 738 274 937 250 = 158 962 555 217 826 360 000. В суммарной сложности, если не учитывать уязвимость «Энигмы» на невозможность шифрования одного и того же символа самим собой, то вышеуказанное количество ключей будет сопоставимо количеству в битовом представлении ~= 267, что грубо (прям очень грубо) говоря больше, чем количество ключей в шифре DES = 256.
Интересной особенностью здесь скорее является даже не количество всех возможных ключей, что для того и сегодняшнего времени всё равно является крайне большим числом (хоть уже и не надёжным со стороны современной криптографии), а комбинация нескольких подстановочных шифров классической криптографии, успешно сочитающихся между собой. Так например, в «Энигме» существуют роторы, представляющие собой полиалфавитный шифр, который при достаточно длинном ключе и его случайности становится сложновзламываемым. Но роторы сами по себе предлагают очень малое количество всех возможных комбинаций, хоть и являются самыми сложными механизмами в «Энигме». На помощь приходят коммутаторы, которые сами по себе не являются надёжными, потому как представляют собой частный случай более общего моноалфавитного шифра — шифра простой подстановки. Шифр простой подстановки хоть и обладает крайне большим количеством ключей 26! = 403 291 461 126 605 635 584 000 000, тем не менее, очень подвержен атакам частотного криптоанализа и атакам по маске. Но так или иначе, «Энигма» показала, что если объединить два этих шифра воедино, то может получиться достаточно хороший синтез, при котором наследуется сложность полиалфавитного шифра и количество ключей моноалфавитного.
Принцип работы
Для упрощения понимания работы шифровальной машины «Энигма» предположим, что у нас существует алфавит всего из восьми символов = {A, B, C, D, E, F, G, H}. Из этого следует, что сами роторы, рефлектор и соответственно коммутаторы ограничены этим же размером. Первое, что нам необходимо сделать — это спроектировать рефлектор и роторы под 8-ми символьный алфавит, как самую базовую основу шифровальной машины «Энигма».
Предположим, что рефлектор имеет следующие связи символов между собой: A=C, B=E, D=H, F=G. Если бы количество символов алфавита было бы нечётным, то шифровальную машину «Энигма» нельзя было бы спроектировать таким образом, каким её проектировали изначально авторы, потому как возникала бы возможность шифрования одного и того же символа самим собой за счёт оставшейся связи рефлектора X=X. Визуально, рефлектор можно изобразить в виде следующей схемы.

Рефлектор с принимаемым (до равно) и выходным (после равно) значениями
Работа рефлектора крайне проста. Если на вход поступает символ A, то рефлектор возвратит нам символ C, если поступает символ H, то рефлектор вернёт символ D и т.д.
Далее, нам необходимо точно таким же образом составить роторы. В отличие от рефлектора, где значения всегда статичны, в роторах значения постоянно меняются. Можно сказать, что каждый ротор представляет собой два диска, где один находится всегда в статичном положении, а другой вращается либо при нажатии символов, либо при совершении полного круга одного из роторов. Для начала создадим один ротор и проведём его к рефлектору. Результат будет выглядить следующим образом.
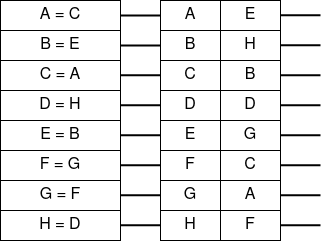
Ротор соединённый с рефлектором
Левая часть ротора для нас будет являться статичной, в то время как правая часть динамична (P.S. наверное лучше было сделать правую часть всё же статичной, а левую динамичной для простоты понимания ввода символов в ротор, тем не менее, механику и получаемый результат такая инверсия никак не изменяет). Ротор — это полиалфавитный шифр, который меняет свой ключ шифрования после каждого введённого символа. Так например, в нашем случае, если мы будем шифровать комбинацию символов AAA, то мы будем получать на выходе ротора результат равный GHA (БЕЗ УЧЁТА РЕФЛЕКТОРА), с условием того, что динамическая часть ротора будет вращаться всегда вниз после нажатого символа.
Теперь, если мы также попытаемся зашифровать комбинацию символов AAA, но пропустим её не только через один ротор, но и последовательно через рефлектор, то получим уже следующий результат: CBE. Суть алгоритма можно представить на примере шифрования первого символа A. Выходом ротора для A будет символ G, символ G попадает на рефлектор и отражается в символ F (потому как таковой является парным), после уже рефлектор подаёт на вход ротору (но в обратном направлении) символ F, который на выходе ротора преобразуется в символ C. Таким образом, символ A шифруется символом C.
На этом же примере мы можем легко проверить, что символ A никогда не зашифруется самим собой, потому как у рефлектора не существует парного символа к самому себе. Для того, чтобы это проверить, достаточно зашифровать 8 раз символ A. На выходе мы будем получать следующий результат: CBEHGBDF (тут главное не ошибиться в количестве сдвигов ротора). Далее, если мы продолжим шифровать символ A, то придём к цикличности шифруемой последовательности, потому как у одного ротора существует только 8 возможных позиций.
Теперь же давайте добавим ещё два ротора с другими вариациями, поставим их последовательно, и проведём их композицию также к рефлектору.
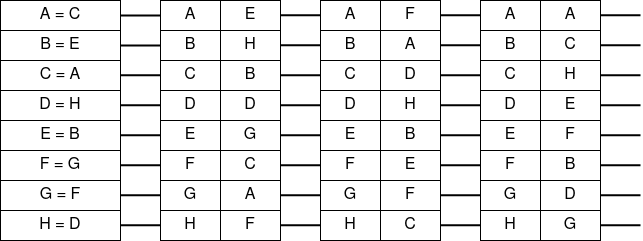
Полная цепь роторов проведённых к рефлектору
Теперь, предположим, что я начинаю шифровать какой-либо символ, тогда по механике «Энигмы» сдвинется только самый ближний ротор к входу, то-есть правый. Как только он совершит свой полный цикл вращения, то на одну позицию повернётся следующий за ним ротор, то-есть средний. Как только средний ротор совершит свой полный цикл, то на одну позицию повернётся следующий за ним ротор, то-есть левый. Такой действие можно продолжать ещё очень долго, но исходя из истории, остановимся только на трёх роторах.
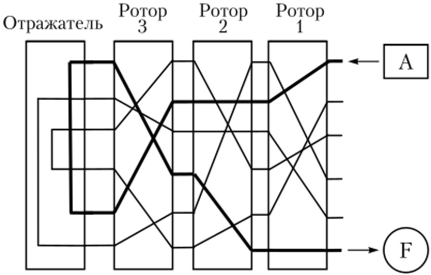
На вышеописанном примере процесс шифрования лучше уже показывать визуально, т.к. система связей значительно усложняется. Так например, если я буду шифровать три раза символ A, то он станет равен сначала символу C, потом символу G, а потом символу E. Это можно показать на следующих схемах.

Первый раунд шифрования символа A
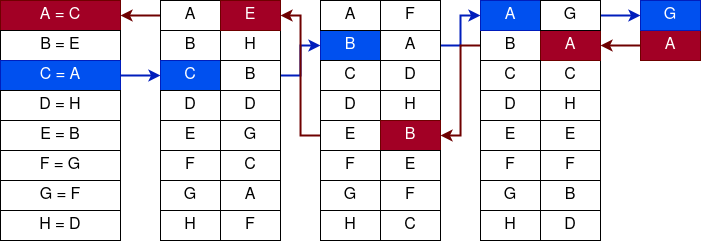
Второй раунд шифрования символа A
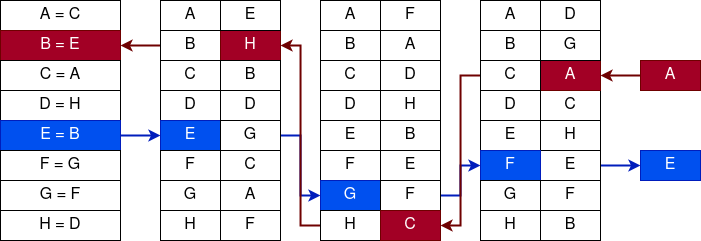
Третий раунд шифрования символа A
Теперь, когда мы разобрались с работой роторов и рефлектора, мы можем усложнить работу «Энигмы» коммутаторами и коммутационной панелью соответственно. Коммутаторы начинают использоваться сразу после ввода символа и перед выходом. В аналогии с современной симметричной криптографией такой механизм можно представить как отбеливающую функцию.
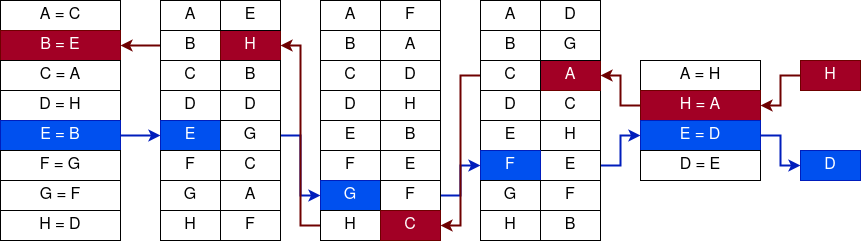
Полная схема шифровальной машины «Энигма»
Примерно таким образом у нас и работает шифровальная машина «Энигма.
Программная реализация
Как мы увидели, основной сложностью реализации для нас будет являться связь нескольких роторов между собой таким образом, чтобы допускался не только поток шифрования в одну сторону к рефлектору, но и от него обратно к начальному ротору. Коммутационная панель будет являться для нас излишним, добавочным механизмом, а потому таковой вы можете попробывать реализовать сами, дополнив код.
Первым делом создаём структуру «Энигмы», которая будет содержать рефлектор (отражатель), роторы, количество используемых роторов, их размер, а также количество произведённых вращений первого ротора.
typedef struct enigma_s {
uint64_t counter;
uint8_t size_rotor;
uint8_t num_rotors;
uint8_t *reflector;
uint8_t **rotors;
} enigma_s;Далее объявляем конструктор и деструктор объектов типа enigma_s, а также функции установки рефлектора и роторов.
extern enigma_s *enigma_new(uint8_t size_rotor, uint8_t num_rotors) {
enigma_s *enigma = (enigma_s*)malloc(sizeof(enigma_s));
if (enigma == NULL) {
return NULL ;
}
enigma->size_rotor = size_rotor;
enigma->num_rotors = num_rotors;
enigma->counter = 0;
enigma->reflector = (uint8_t*)malloc(sizeof(uint8_t)*size_rotor);
enigma->rotors = (uint8_t**)malloc(sizeof(uint8_t*)*num_rotors);
for (int i = 0; i < num_rotors; ++i) {
enigma->rotors[i] = (uint8_t*)malloc(sizeof(uint8_t)*size_rotor);
}
return enigma;
}
extern void enigma_free(enigma_s *enigma) {
for (int i = 0; i < enigma->num_rotors; ++i) {
free(enigma->rotors[i]) ;
}
free(enigma->rotors);
}
extern void enigma_set_reflector(enigma_s *enigma, uint8_t *reflector) {
for (int i = 0; i < enigma->size_rotor; ++i) {
enigma->reflector[i] = reflector[i];
}
}
extern void enigma_set_rotor(enigma_s *enigma, uint8_t num, uint8_t *rotor) {
for (int i = 0; i < enigma->size_rotor; ++i) {
enigma->rotors[num][i] = rotor[i];
}
}Теперь приступим к кульминационному моменту, а именно шифрованию. Мы знаем, что особенностью «Энигмы» является не только её «машинная среда», но также и инволютивность шифрования/расшифрования. Иными словами, в «Энигме» не существует переключателей между шифрованием и расшифрованием, потому как шифрование = расшифрование. Единственным разделяющим моментом здесь служат позиции роторов и их настройка.
// На вход подаётся состояние «Энигмы» (enigma) и шифруемое число (code).
// На выходе получаем зашифрованное число (code) и успешность выполнения (valid).
// code - это закодированный символ вида A=0, B=1, C=2, ..., X=23, Y=24, Z=25.
extern uint8_t enigma_encrypt(enigma_s *enigma, uint8_t code, int *valid) {
uint64_t rotor_queue;
uint8_t new_code;
// Проверяем, что code принадлежит диапазону алфавита от 0 до 25 включительно.
// Иначе свидетельствуем об ошибке выполнения.
if (code > enigma->size_rotor) {
*valid = 0;
return 0;
}
// Используем переменную, которая будет являться состоянием
// шифруемого символа.
new_code = code;
// Проходим сквозь все роторы в сторону рефлектора, постоянно обновляя состояние символа.
// Символ в такой концепции представляет собой индекс массива, по которому находим новый символ как значение массива.
for (int i = 0; i < enigma->num_rotors; ++i) {
new_code = enigma->rotors[i][new_code];
}
// Получаем новое состояние символа от рефлектора.
new_code = enigma->reflector[new_code];
// Теперь проходим сквозь все роторы, но уже от рефлектора, также постоянно обновляя состояние символа.
// Символ в такой концепции представляет собой значение массива, по которому находим новый символ как индекс массива.
for (int i = enigma->num_rotors-1; i >= 0; --i) {
new_code = enigma_rotor_find(enigma, i, new_code, valid);
if (*valid == 0) {
return 0;
}
}
// После того, как прошли по роторам в сторону рефлектора и обратно
// настало время обновить состояние самих роторов, их позицию.
// Увеличиваем счётчик шифрованных символов и устанавливаем
// по умолчанию очередь ротора = 1.
// Это говорит о том, что первый ротор должен обновлять своё состояние
// каждый введённый символ.
rotor_queue = 1;
enigma->counter += 1;
for (int i = 0; i < enigma->num_rotors; ++i) {
// Обновляем состояние ротора по его очереди.
if (enigma->counter % rotor_queue == 0) {
enigma_rotor_shift(enigma, i);
}
// Увеличиваем очередь каждого последующего ротора, т.к.
// поворот одного ротора должен производиться только после полного
// цикла предыдущего ротора.
rotor_queue *= enigma->size_rotor;
}
// Возвращаем шифрованный символ.
*valid = 1;
return new_code;
}
// Функция обычного сдвига массива на одну единицу вправо.
static void enigma_rotor_shift(enigma_s *enigma, uint8_t num) {
char temp = enigma->rotors[num][enigma->size_rotor-1];
for (int i = enigma->size_rotor-1; i > 0; --i) {
enigma->rotors[num][i] = enigma->rotors[num][i-1];
}
enigma->rotors[num][0] = temp;
}
// Функция обычного нахождения элемента в массиве.
static uint8_t enigma_rotor_find(enigma_s *enigma, uint8_t num, uint8_t code, int *valid) {
for (int i = 0; i < enigma->size_rotor; ++i) {
if (enigma->rotors[num][i] == code) {
*valid = 1;
return i;
}
}
*valid = 0;
return 0;
}Чтобы шифровать не закодированные символы, а конкретно символы, мы можем написать функции кодирования/декодирования поступаемых символов или кодов непосредственно.
Код кодировщика
extern encoder_t *encoder_new(uint8_t size_alph) {
encoder_t *encoder = (encoder_t*)malloc(sizeof(encoder_t));
if (encoder == NULL) {
return NULL;
}
encoder->size_alph = size_alph;
encoder->alphabet = (uint8_t*)malloc(sizeof(uint8_t)*size_alph);
return encoder;
}
extern void encoder_free(encoder_t *encoder) {
free(encoder->alphabet);
free(encoder);
}
extern void encoder_set_alphabet(encoder_t *encoder, uint8_t *alphabet) {
for (int i = 0; i < encoder->size_alph; ++i) {
encoder->alphabet[i] = alphabet[i];
}
}
extern uint8_t encoder_encode(encoder_t *encoder, uint8_t ch, int *found) {
for (int i = 0; i < encoder->size_alph; ++i) {
if (encoder->alphabet[i] == ch) {
*found = 1;
return i;
}
}
*found = 0;
return 0;
}
extern uint8_t encoder_decode(encoder_t *encoder, uint8_t code, int *valid) {
if (code >= encoder->size_alph) {
*valid = 0;
return 0;
}
*valid = 1;
return encoder->alphabet[code];
}Далее, всё что нам остаётся сделать — это создать конкретные роторы и рефлектор, привязать их к объекту «Энигмы», создать объект кодировщика, а также для полноты реализовать ввод текста.
Установка роторов и рефлектора в «Энигму»
uint8_t num_rotors = 3;
uint8_t reflector[] = {25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
uint8_t *rotors[] = {
(uint8_t[]){0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25},
(uint8_t[]){20, 21, 22, 23, 24, 25, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
(uint8_t[]){7, 6, 5, 4, 3, 2, 1, 0, 24, 23, 22, 21, 20, 25, 8, 9, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10},
};
enigma_s *enigma = enigma_new(size_alph, num_rotors);
enigma_set_reflector(enigma, reflector);
for (int i = 0; i < num_rotors; ++i) {
enigma_set_rotor(enigma, i, rotors[i]);
}
...
// Не забываем освободить память объекта «Энигмы» после выполнения всех действий.
enigma_free(enigma);Создание кодировщика
uint8_t alphabet[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
uint8_t size_alph = (uint8_t)strlen((char*)alphabet);
encoder_t *encoder = encoder_new(size_alph);
encoder_set_alphabet(encoder, alphabet);
...
// Не забываем освободить память объекта кодировщика после выполнения всех действий.
encoder_free(enigma);uint8_t enc_ch, dec_ch;
int ch, flag;
while(1) {
ch = getchar();
// Остановить шифрование после введённого символа ~
if (ch == '~') {
putchar('\n');
break;
}
// Кодируем символ в числовое представление вида A=0, B=1, C=2, ...
enc_ch = encoder_encode(encoder, (uint8_t)ch, &flag);
if (flag == 0) {
// Если не получается закодировать -> просто выводим этот символ.
putchar(ch);
continue;
}
// Шифруем код символа.
enc_ch = enigma_encrypt(enigma, enc_ch, &flag);
if (flag == 0) {
fprintf(stderr, "\nencoder put to enigma unknown code (%d)\n", enc_ch);
break;
}
// Декодируем код шифрованного символа.
dec_ch = encoder_decode(encoder, enc_ch, &flag);
if (flag == 0) {
fprintf(stderr, "\nenigma put to decoder unknown code (%d)\n", enc_ch);
break;
}
// Выводим шифрованный символ.
putchar(dec_ch);
}Запускаем приложение и проверяем его работу на примере шифрования.
> AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
FWYMCEMOQVXWWDFEEOKMOVXZBDWYMCEMOQVXWWDFEEOKMOVXZBDFYMCEMOQVXWWDFEEOKMOVXZBDFWMCEMOQVXWWDFEEOKMOVXZBDFWYCEMOТеперь попытаемся расшифровать полученный результат. Для этого останавливаем работу приложения и вновь его запускаем, чтобы состояние машины «Энигма» выставилась на начальные позиции.
> FWYMCEMOQVXWWDFEEOKMOVXZBDWYMCEMOQVXWWDFEEOKMOVXZBDFYMCEMOQVXWWDFEEOKMOVXZBDFWMCEMOQVXWWDFEEOKMOVXZBDFWYCEMO
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAМожем теперь зашифровать и что-то более нормальное.
> HELLOWORLD
TDZVSRYVKPЗаключение
В ходе проделанной работы мы рассмотрели не только то, как шифровальная машина «Энигма» работает изнутри, но и также смогли реализовать её на языке программирования Си. В коде мы только не затронули использование коммутаторов, но это крайне легко сделать, дополнив код функциями шифрования до вызова функции enigma_encrypt и соответственно после (либо, что более правильно, прописать это внутри самой функции enigma_encrypt).
Полный исходный код шифровальной машины «Энигма»
#include
#include
#include
#include
// ENCODER
typedef struct encoder_t {
uint8_t size_alph;
uint8_t *alphabet;
} encoder_t;
extern encoder_t *encoder_new(uint8_t size_alph);
extern void encoder_free(encoder_t *encoder);
extern void encoder_set_alphabet(encoder_t *encoder, uint8_t *alphabet);
extern uint8_t encoder_encode(encoder_t *encoder, uint8_t ch, int *found);
extern uint8_t encoder_decode(encoder_t *encoder, uint8_t code, int *valid);
// ENIGMA
typedef struct enigma_s {
uint64_t counter;
uint8_t size_rotor;
uint8_t num_rotors;
uint8_t *reflector;
uint8_t **rotors;
} enigma_s;
extern enigma_s *enigma_new(uint8_t size_rotor, uint8_t num_rotors);
extern void enigma_free(enigma_s *enigma);
extern void enigma_set_reflector(enigma_s *enigma, uint8_t *reflector);
extern void enigma_set_rotor(enigma_s *enigma, uint8_t num, uint8_t *rotor);
extern uint8_t enigma_encrypt(enigma_s *enigma, uint8_t code, int *valid);
static void enigma_rotor_shift(enigma_s *enigma, uint8_t num);
static uint8_t enigma_rotor_find(enigma_s *enigma, uint8_t num, uint8_t code, int *valid);
int main(void) {
// INIT ENCODER
uint8_t alphabet[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
uint8_t size_alph = (uint8_t)strlen((char*)alphabet);
encoder_t *encoder = encoder_new(size_alph);
encoder_set_alphabet(encoder, alphabet);
// INIT ENIGMA
uint8_t num_rotors = 3;
uint8_t reflector[] = {25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
uint8_t *rotors[] = {
(uint8_t[]){0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25},
(uint8_t[]){20, 21, 22, 23, 24, 25, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
(uint8_t[]){7, 6, 5, 4, 3, 2, 1, 0, 24, 23, 22, 21, 20, 25, 8, 9, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10},
};
enigma_s *enigma = enigma_new(size_alph, num_rotors);
enigma_set_reflector(enigma, reflector);
for (int i = 0; i < num_rotors; ++i) {
enigma_set_rotor(enigma, i, rotors[i]);
}
// INPUT CHARS
uint8_t enc_ch, dec_ch;
int ch, flag;
while(1) {
ch = getchar();
// STOP IF CHAR = '~'
if (ch == '~') {
putchar('\n');
break;
}
// ENCODE
enc_ch = encoder_encode(encoder, (uint8_t)ch, &flag);
if (flag == 0) {
// just print unknown char
putchar(ch);
continue;
}
// ENCRYPT/DECRYPT
enc_ch = enigma_encrypt(enigma, enc_ch, &flag);
if (flag == 0) {
fprintf(stderr, "\nencoder put to enigma unknown code (%d)\n", enc_ch);
break;
}
// DECODE
dec_ch = encoder_decode(encoder, enc_ch, &flag);
if (flag == 0) {
fprintf(stderr, "\nenigma put to decoder unknown code (%d)\n", enc_ch);
break;
}
putchar(dec_ch);
}
// FREE ENCODER AND ENIGMA
encoder_free(encoder);
enigma_free(enigma);
return 0;
}
// ENCODER
extern encoder_t *encoder_new(uint8_t size_alph) {
encoder_t *encoder = (encoder_t*)malloc(sizeof(encoder_t));
if (encoder == NULL) {
return NULL;
}
encoder->size_alph = size_alph;
encoder->alphabet = (uint8_t*)malloc(sizeof(uint8_t)*size_alph);
return encoder;
}
extern void encoder_free(encoder_t *encoder) {
free(encoder->alphabet);
free(encoder);
}
extern void encoder_set_alphabet(encoder_t *encoder, uint8_t *alphabet) {
for (int i = 0; i < encoder->size_alph; ++i) {
encoder->alphabet[i] = alphabet[i];
}
}
extern uint8_t encoder_encode(encoder_t *encoder, uint8_t ch, int *found) {
for (int i = 0; i < encoder->size_alph; ++i) {
if (encoder->alphabet[i] == ch) {
*found = 1;
return i;
}
}
*found = 0;
return 0;
}
extern uint8_t encoder_decode(encoder_t *encoder, uint8_t code, int *valid) {
if (code >= encoder->size_alph) {
*valid = 0;
return 0;
}
*valid = 1;
return encoder->alphabet[code];
}
// ENIGMA
extern enigma_s *enigma_new(uint8_t size_rotor, uint8_t num_rotors) {
enigma_s *enigma = (enigma_s*)malloc(sizeof(enigma_s));
if (enigma == NULL) {
return NULL ;
}
enigma->size_rotor = size_rotor;
enigma->num_rotors = num_rotors;
enigma->counter = 0;
enigma->reflector = (uint8_t*)malloc(sizeof(uint8_t)*size_rotor);
enigma->rotors = (uint8_t**)malloc(sizeof(uint8_t*)*num_rotors);
for (int i = 0; i < num_rotors; ++i) {
enigma->rotors[i] = (uint8_t*)malloc(sizeof(uint8_t)*size_rotor);
}
return enigma;
}
extern void enigma_free(enigma_s *enigma) {
for (int i = 0; i < enigma->num_rotors; ++i) {
free(enigma->rotors[i]) ;
}
free(enigma->rotors);
}
extern void enigma_set_reflector(enigma_s *enigma, uint8_t *reflector) {
for (int i = 0; i < enigma->size_rotor; ++i) {
enigma->reflector[i] = reflector[i];
}
}
extern void enigma_set_rotor(enigma_s *enigma, uint8_t num, uint8_t *rotor) {
for (int i = 0; i < enigma->size_rotor; ++i) {
enigma->rotors[num][i] = rotor[i];
}
}
extern uint8_t enigma_encrypt(enigma_s *enigma, uint8_t code, int *valid) {
uint64_t rotor_queue;
uint8_t new_code;
if (code >= enigma->size_rotor) {
*valid = 0;
return 0;
}
new_code = code;
// code -> rotors
for (int i = 0; i < enigma->num_rotors; ++i) {
new_code = enigma->rotors[i][new_code];
}
// code -> reflector
new_code = enigma->reflector[new_code];
// reflector -> code
// rotors -> code
for (int i = enigma->num_rotors-1; i >= 0; --i) {
new_code = enigma_rotor_find(enigma, i, new_code, valid);
if (*valid == 0) {
return 0;
}
}
// shift rotors
rotor_queue = 1;
enigma->counter += 1;
for (int i = 0; i < enigma->num_rotors; ++i) {
if (enigma->counter % rotor_queue == 0) {
enigma_rotor_shift(enigma, i);
}
rotor_queue *= enigma->size_rotor;
}
*valid = 1;
return new_code;
}
static void enigma_rotor_shift(enigma_s *enigma, uint8_t num) {
char temp = enigma->rotors[num][enigma->size_rotor-1];
for (int i = enigma->size_rotor-1; i > 0; --i) {
enigma->rotors[num][i] = enigma->rotors[num][i-1];
}
enigma->rotors[num][0] = temp;
}
static uint8_t enigma_rotor_find(enigma_s *enigma, uint8_t num, uint8_t code, int *valid) {
for (int i = 0; i < enigma->size_rotor; ++i) {
if (enigma->rotors[num][i] == code) {
*valid = 1;
return i;
}
}
*valid = 0;
return 0;
} Список литературы
Тайная история шифров и их расшифровки. С. Сингх
Основы классической криптологии. М. Адаменко
https://www.youtube.com/watch? v=eJXmdi41Z2U&t=165s (не совсем литература)
https://habr.com/ru/company/ua-hosting/blog/450186/
https://ru.wikipedia.org/wiki/Энигма
