Прогнозирование временных рядов методом рядов Фурье

Привет, Хабр.
Эта статья посвящена методу долгосрочного прогнозирования временных рядов с помощью рядов Фурье [1–2]. Особенность подхода в том, что в отличие от классических методов прогнозирования и машинного обучения прогнозируется не сама неизвестная функция, а ее коэффициенты разложения в ряд Фурье. Далее по спрогнозированным коэффициентам Фурье восстанавливается неизвестная функция и делается прогноз ее значений на следующий период.
Внимание! Статья содержит множество формул.
Схематично данный метод можно проиллюстрировать следующей анимацией

Тем, кто с мехмата/матфака хорошо знаком с такими понятиями, как временные ряды и ряды Фурье, можно пропустить первые три раздела данной статьи.
Временной ряд — значения некоторой величины, измеренные через равные промежутки времени
где
Задача прогнозирования временных рядов заключается в нахождении функции F:
где
Т.е. по известным значениям ряда из прошлого необходимо найти его значения в будущем.
Замечание: при прогнозировании временных рядов предполагается, что прошлые значения ряда содержат информацию о его поведении в будущем. В классических же задачах анализа данных считается, что различные наблюдения независимы.
Пусть функция
является ортонормальной на
$$display$$\int_a^b φ_i (x) φ_j (x)dx= δ_{ik} = \begin{cases} 1 &\text{$i = k$}\\ 0 &\text{$i \neq k$} \end{cases}. \;\;\;(4)$$display$$
Обозначим
тогда ряд
$$display$$a_1φ_1 (x)+a_2φ_2 (x)+⋯+a_kφ_k (x)+⋯ \;\;\; (6)$$display$$
называется рядом Фурье. Коэффициенты (5) этого ряда называются коэффициентами Фурье функции f (x) по системе (3).
Ряд Фурье — разложение некоторой функции по полной системе ортонормированных функций (по некоторому базису).
Тригонометрические ряды Фурье
Если в качестве системы (3) взять ортонормированную на отрезке систему функций
то разложение произвольной функции f (x) по системе (7) в ряд Фурье на отрезке
где коэффициентыи
Ряд (8) называется тригонометрическим рядом Фурье. Ряды Фурье по другим системам называют обобщенными рядами Фурье. Далее для краткости под рядом Фурье будем понимать именно тригонометрический ряд Фурье, т.к. в данной статье мы будем иметь дело только с ним.
Теорема Дирихлe: Если функция f (x) задана на отрезке и является на нем кусочно-непрерывной, кусочно-монотонной и ограниченной, то ее тригонометрический ряд Фурье сходится во всех точках отрезка. Если s (x) — сумма тригонометрического ряда Фурье функции f (x), то во всех точках непрерывности этой функции
А во всех точках разрыва
Кроме этого,
Среди всех тригонометрических многочленов
$$display$$\frac{α_0}{2}+\sum_{k=1}^{N}α_k\cos(kx)+β_k\sin(kx)$$display$$
с заданным N частичная сумма ряда Фурье
дает наилучшую (в метрике пространства функций с интегрируемым квадратом на отрезке
Пусть f (t) — функция с интегрируемым квадратом на отрезке
Для этой функции, заданной на отрезке
где
Дан временной ряд, содержащий m значений:
Нужно спрогнозировать значение
Одним из методов прогнозирования на один шаг является метод построения матрицы задержек. Суть метода заключается в следующем [4–5]: выбирается некоторое число p — величина задержек, подбирается зависимость значения
Вид зависимости, как правило, выбирается линейный
Для определения коэффициентов
Если m не кратно p то можно отбросить несколько первых членов ряда. В последней строке выбирается множество S — так называемое множество «ближайших соседей» к значению
Коэффициенты
где
Из необходимого условия минимума
получаем систему уравнений для нахождения коэффициентов
Можно воспользоваться матричной записью выражения (13)
и вспомнить аналитическое решение данной задачи:
Подставляя полученный вектор
Далее метод прогнозирования на один шаг будет использоваться для прогнозирования коэффициентов Фурье на следующий период.
Постоянная длина периода
Пусть дан временной ряд значений некоторого показателя
при этом для значений последовательности (14) наблюдается определенная периодичность. Для исследования временного ряда (14) с постоянной периодичностью (например, продажи какого-либо товара по неделям) предлагается [1–2] использовать тригонометрические ряды Фурье. В этом случае весь набор наблюдений s можно разбить на m периодов длины l+1, а массив измерений (14) можно представить в виде матрицы
размерности
Значения
$$display$$\begin{aligned} &f_{i}(t)\approx y_i (t), \\ y_i (t) = \frac{a_0^i}{2}+&\sum_{k=1}^{N}a_k^i\cos\Bigl (\frac{\pi kt}{l}\Bigr). \end{aligned} \;\;\;(16)$$display$$
Таким образом, получаем для каждого i-го периода частичную сумму ряда Фурье со своими коэффициентами
1 метод. Минимизация квадратичной ошибки
где
получаем систему уравнений для нахождения коэффициентов
Количество слагаемых N в этом случае нужно выбирать не более длины периода l.
2 метод. Непосредственно из формулы
Если выбрать N = l, то из формул (16) для определения коэффициентов получаем систему уравнений
3 метод. Численное интегрирование
Вспомним, что
Если длина периода l>20, то для нахождения коэффициентов
После того, как коэффициенты найдены, строится прогноз для следующего периода по формуле
Переменная длина периода
Пусть теперь длина периода не является постоянной (например, количество дней в месяце). Пусть l — длина i-го периода, i=1, 2, …, m. Для каждого периода i имеем последовательность значений
Пусть вновь
Обозначим
Тогда
$$display$$\begin{aligned} &\widetilde{f}_{i}(x)\approx y_i (x), \\ y_i (t) = \frac{a_0^i}{2}+\sum_{k=1}^{N}&a_k^i\cos(kx)+b_k^i\sin(kx), \end{aligned} \;\;\;(19)$$display$$
где
Коэффициенты
где
Таким образом, способ нахождения коэффициентов Фурье для каждого периода зависит от постоянства длин периодов и от их длины. Значения найденных коэффициентов в зависимости от номера периода рассматриваем как временные ряды, которые нужно спрогнозировать на один следующий шаг.
Коэффициенты ряда Фурье
прогнозируются с помощью матрицы задержек (для каждого коэффициента строится своя матрица задержек). Далее, используя полученные значения этих коэффициентов, можно построить прогноз на следующий период по формуле
$$display$$\begin{aligned} y_{m+1}(t) = &\frac{a_0^{m+1}}{2}+\sum_{k=1}^{N}a_k^{m+1}\cos(kx)+b_k^{m+1}\sin(kx), \\ &x_t=\frac{2\pi t}{l_{m+1}}-\pi, \;\; t=1,2,…, l_{m+1}. \end{aligned}\;\;\; (21)$$display$$
Резюмируем: для долгосрочного прогнозирования временных рядов
- Наблюдения каждого периода (каждой недели или каждого месяца)
объявляются значениями некоторой функции
- Функция
заменяется частной суммой ряда Фурье
- Из условия минимума квадратичной ошибки (20) или каким-либо другим способом находятся коэффициенты ряда Фурье для известных периодов
- Найденные коэффициенты рассматриваются как временные ряды в зависимости от номера периода
- Для каждого коэффициента строится своя матрица задержек и делается прогноз этого коэффициента на следующий период
- По спрогнозированным коэффициентам Фурье по формуле (21) находятся значения неизвестной функции (временного ряда) для следующего периода
Попробуем применить данный алгоритм на реальных данных. Возьмем с сайта Росстата среднюю зарплату в России по месяцам за период с 2013-го по 2018-й г.
import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error
sns.set()
data = pd.read_excel('mean_salary.xlsx')
data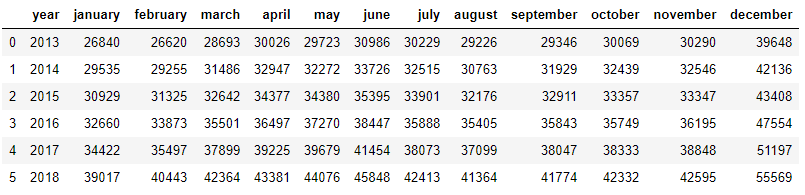
Преобразуем данные в удобный формат в виде ряда и построим график
#сюда положим ряд, составленный из средних зп
salary_series = pd.Series()
for _, row in data.drop('year', axis=1).iterrows():
salary_series = salary_series.append(pd.Series(row.values))
#используем даты в качестве индексов
salary_series.index = pd.date_range('2013-01-01', freq='M', periods=6*12)
#построим график
salary_series.plot(figsize=(12, 6), linewidth=2, fontsize=13)
plt.title('Среднемесячная ЗП в России', fontsize=15)
plt.show()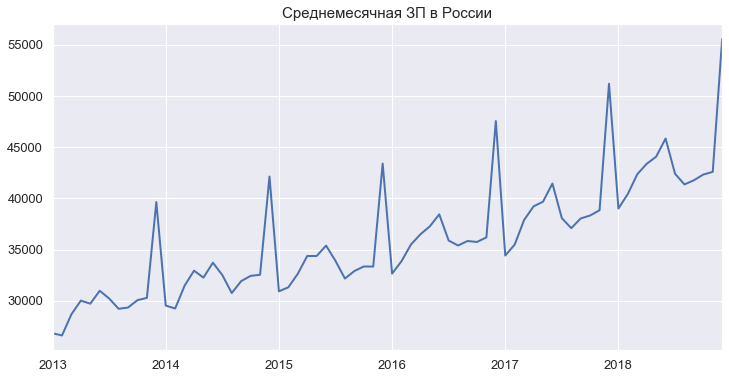
Разделим данные на тренировочный (2013 — 2017 гг.) и тестовый (2018 г.) наборы.
train_series = salary_series[salary_series.index.year<2018]
test_series = salary_series[salary_series.index.year==2018]Перейдем к реализации алгоритма. Наш временной ряд состоит из 5-ти периодов одинаковой длины (12 месяцев), поэтому будем представлять неизвестную функцию в виде формулы (16). Для поиска коэффициентов
def cos(k, t, l):
"""
Вспомогательная функция косинуса
"""
return math.cos(math.pi*k*t/l)
def get_matrix_and_vector(period_i: np.ndarray) -> (np.ndarray, np.ndarray):
"""
Возвращает матрицу и вектор свободных членов для нахождения коэффициентов Фурье для i-го периода.
period_i - наблюдения i-го периода
"""
l = len(period_i) - 1
N = l
y = np.empty((0,))
matrix = np.empty((0, N+1))
for t in range(0, l+1):
#первое значение в каждой строке 1/2 -- множитель перед коэффициентом a_0
row = np.array([.5])
for k in range(1, N+1):
row = np.append(row, cos(k, t, l))
row = np.reshape(row, (1, N+1))
matrix = np.append(matrix, row, axis=0)
y = np.append(y, period_i[t])
return matrix, y
def solve_system(M: np.ndarray,
b: np.ndarray) -> np.ndarray:
"""
Решает систему линейных уравнений
M - основная матрица системы
b - столбец свободных членов
"""
assert np.linalg.det(M) != 0
return np.linalg.solve(M, b)Далее реализуем функцию для преобразования входного ряда в матрицу, функции построения матрицы задержек, поиска ближайших соседей и прогнозирования на один шаг.
def get_matrix_from_series(input_series: pd.Series,
m: int,
l: int):
"""
Преобразует входной ряд в матрицу,
где каждая i-я строка -- наблюдения для i-го периода
input_series -- входной ряд
m -- количество периодов
l - длина периода
"""
return input_series.values.reshape(m, l)
def get_delay_matrix(input_vector: np.ndarray,
p: int = 1) -> np.ndarray:
"""
Строит матрицу задержек по входному вектору и величине задержек
input_vector - входной вектор
p - величина задержек
"""
input_vector_copy = np.copy(input_vector)
m = input_vector_copy.shape[0] % p
#если длина ряда не кратна p, то удаляем несколько первых значений ряда
if m != 0:
input_vector_copy = np.delete(input_vector_copy, range(m))
#определяем размерность матрицы зарежек
row_dim = input_vector_copy.shape[0] // p
col_dim = p
#строим матрицу
delay_matrix = np.resize(input_vector_copy,
new_shape=(row_dim, col_dim)).T
return delay_matrix
def find_nearest(row: np.ndarray,
p: int) -> set:
"""
Возвращает индексы ближайших соседей для последнего элемента строки
row - входная строка
p - величина задержек
"""
#количество соседей
neighbors_cnt = 2 * p + 1
last_element = row[-1]
all_neighbors = row[:-1]
#находим индексы ближайших соседей
idx = set(np.argsort(np.abs(all_neighbors-last_element))[:neighbors_cnt])
return idx
def predict_by_one_step(input_vector: np.ndarray,
p: int = 1) -> float :
"""
Прогнозирование на один шаг с помощью аналитического решения
input_vector - входной вектор
p - величина задержек
"""
delay_matrix = get_delay_matrix(input_vector, p)
last_row = delay_matrix[-1,:]
nearest_neighbors_indexes = find_nearest(last_row, p)
y = np.empty((0,))
X = np.empty((0, p+1))
for index in nearest_neighbors_indexes:
y = np.append(y, delay_matrix[0, index+1])
row = np.append(np.array([1]), delay_matrix[:, index])
row = np.reshape(row, (1, p+1))
X = np.append(X, row, axis=0)
coef = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
prediction = sum(np.append(np.array([1]), delay_matrix[:, -1]) * coef)
return predictionНаконец реализуем функцию поиска коэффициентов для неизвестного периода и функцию прогнозирования временного ряда на следующий период.
def get_new_fourier_coefs(periods: np.ndarray,
p: int = 1) -> list:
"""
Возвращает коэффициенты Фурье для неизвестного периода
periods - матрица наблюдений для известных периодов, где i-я строчка -- наблюдения i-го периода
p - величина задержек
"""
#список с предсказанными на след. период коэффициентами
new_coefs = []
#матрица с коэффициентами Фурье за все периоды. Строки -- коэфициенты за период
coefs_for_all_periods = []
for period in periods:
X, y = get_matrix_and_vector(period)
#находим коэффициенты Фурье, как решение системы линейных уравнений
fourier_coef_for_period = solve_system(X, y)
coefs_for_all_periods.append(fourier_coef_for_period)
coefs_for_all_periods = np.array(coefs_for_all_periods)
#Прогноз каждого коэффициента Фурье a_k для неизвестного периода
#Каждый коэф. Фурье рассматривается как временной ряд, который прогнозируется на один шаг
for i in range(coefs_for_all_periods.shape[1]):
coef_for_next_period = predict_by_one_step(coefs_for_all_periods[:, i], p=p)
new_coefs.append(coef_for_next_period)
return new_coefs
def predict_next_period(new_coefs: list,
l: int):
"""
Прогнозирует временной ряд на неизвестный период
new_coefs - коэффициенты Фурье для следующего периода
l - длина периода
"""
new_period = []
for t in range(0, l):
s = new_coefs[0] / 2
for k in range(1, len(new_coefs)):
s += new_coefs[k]*cos(k, t, l=l-1)
new_period.append(s)
return new_periodПредскажем тестовый период и сравним с реальными результатами.
m = 5 #количество периодов в train выборке
l = 12 #длина периода
p = 1 #величина задержек
matrix = get_matrix_from_series(train_series, m, l)
new_coefs = get_new_fourier_coefs(matrix, p)
test_pred = predict_next_period(new_coefs, l)
test_pred = pd.Series(test_pred, index=test_series.index)
#ошибка прогноза
mae = round(mean_absolute_error(test_pred, test_series), 2)
mape = round(mean_absolute_percentage_error(test_series, test_pred), 3)
#построим график
test_pred.plot(figsize=(12, 6), linewidth=3,
fontsize=13, label='Прогноз')
test_series.plot(figsize=(12, 6), linewidth=3,
fontsize=13, label='Факт')
plt.legend(fontsize=15)
plt.text(test_series.index[4], 55000, f'Mean absolute error = {mae}', fontsize=15)
plt.text(test_series.index[4], 54000, f'Mean absolute percentage error = {mape}', fontsize=15)
plt.title('Сравнение прогноза и факта среднемесячной ЗП в РФ на 2018-й год', fontsize=15)
plt.show()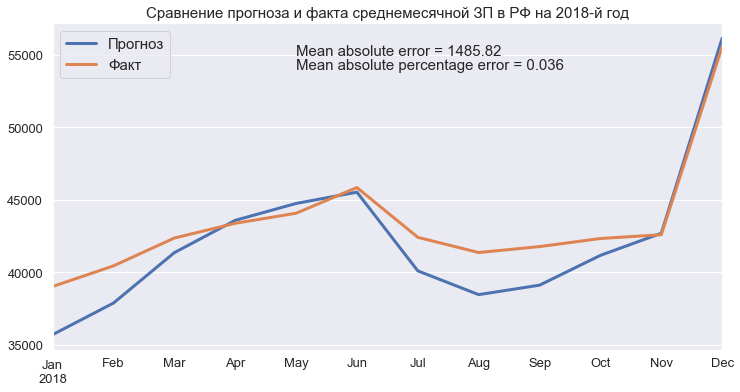
Весь код и данные доступны по ссылке на гитхабе.
- П.А. Гатин, В.Н. Семенова, Исследование циклических временных рядов с переменной цикличностью методом рядов Фурье, Вестник ДИТИ, 2018. — № 1(15). — С. 91–96
- П.А. Гатин, В.Н. Семенова, Об одном подходе к исследованию временных рядов с постоянной цикличностью, ДИТИ НИЯУ МИФИ, 2017. — С. 48–51
- А.Н. Колмогоров, С.В. Фомин — Элементы теории функций и функционального анализа
- В.Н. Афанасьев, М.М. Юзбашев, Анализ временных рядов и прогнозирование — М.: Финансы и статистика, Инфра-М, 2010. — 320 c.
- А.Ю. Лоскутов, О.Л. Котляров, И.А. Истомин, Д.И. Журавлев. Проблемы нелинейной динамики. III. Локальные методы прогнозирования временных рядов. Вестн. Моск. ун-та, сеp. Физ.-астр., 2002, No6, c. 3–21.
- О.С. Амосов, О.С., Муллер Н.В. Исследование временных рядов с применением методов фрактального и вейвлет анализа, Интернет-журнал «НАУКОВЕДЕНИЕ», Выпуск 3
