Проектируем космическую ракету с нуля. Часть 4 — Второй закон Кеплера02.09.2019 18:19

Содержание

Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Часть 3 — Ужепочти-решение задачи двух тел

Второй закон Кеплера

Всем привет! В прошлый раз мы остановились на вот этих уравнениях:
\begin{equation*}
\begin{cases}
\ddot{x} = -\mu \dfrac{x}{(x^{2}+y^{2})^{\frac{3}{2}}},
\\
\ddot{y} = -\mu \dfrac{y}{(x^{2}+y^{2})^{\frac{3}{2}}}.
\end{cases}
\end{equation*}
Задачка теперь плоская, все будет — хорошо. Запустим численное моделирование и отрисуем несколько траекторий движения (для разных начальных условий). Не анимацию, как раньше, а чтобы видно было какие формы имеют линии:

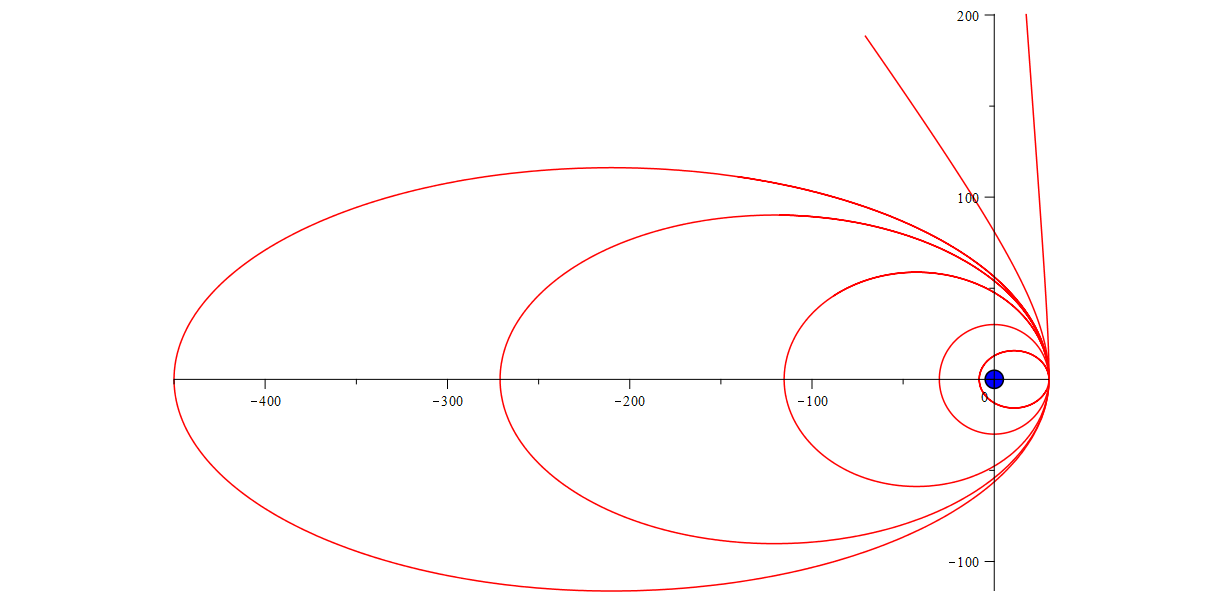
Возможные траектории движения спутника

Те кто знаком с эллипсами сразу скажут: тю, так это похоже эллипсы!

А те кто не слышал о эллипсах скажут: овал. Или сплюснутый кружок.
Но все ли линии тут «эллипсы»? Последние две не дорисованы, но видимо, если их продлить, то они замкнуться и станут очень большими эллипсами? Ну давайте продлим одну их них, ту что посередине.

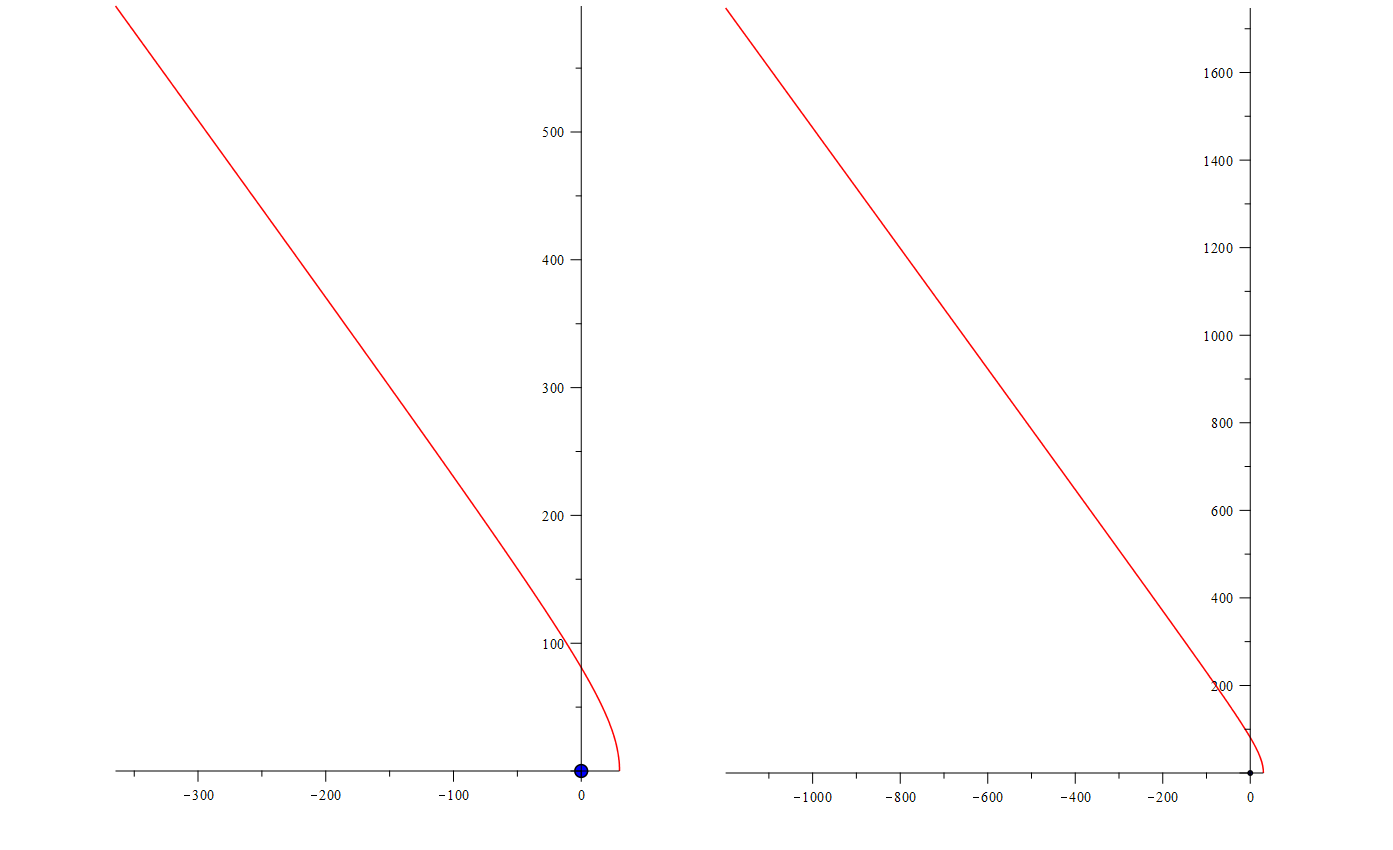
Не похоже на эллипс

В прямую что-ли превращается… Превращается. Знающие эллипс — знают и гиперболу. И только взглянув на картинку, слово вам даю, — это слово они прокричали во весь голос. А потом к ним пришла мысль: тю, так это коники — конические сечения. Ждать ли нам еще и параболу? И уравнение им ответит: ждите.

Так, те кто не слишком понимает о чём идет речь — не переживайте. Дальше растолкуем. Пока это не принципиально, пока мы просто численно моделировали, чтобы прикинуть:, а что всё-таки приблизительно должно получиться.

Ну и на закуску можно еще разок взглянуть как летает в плоскости спутник:

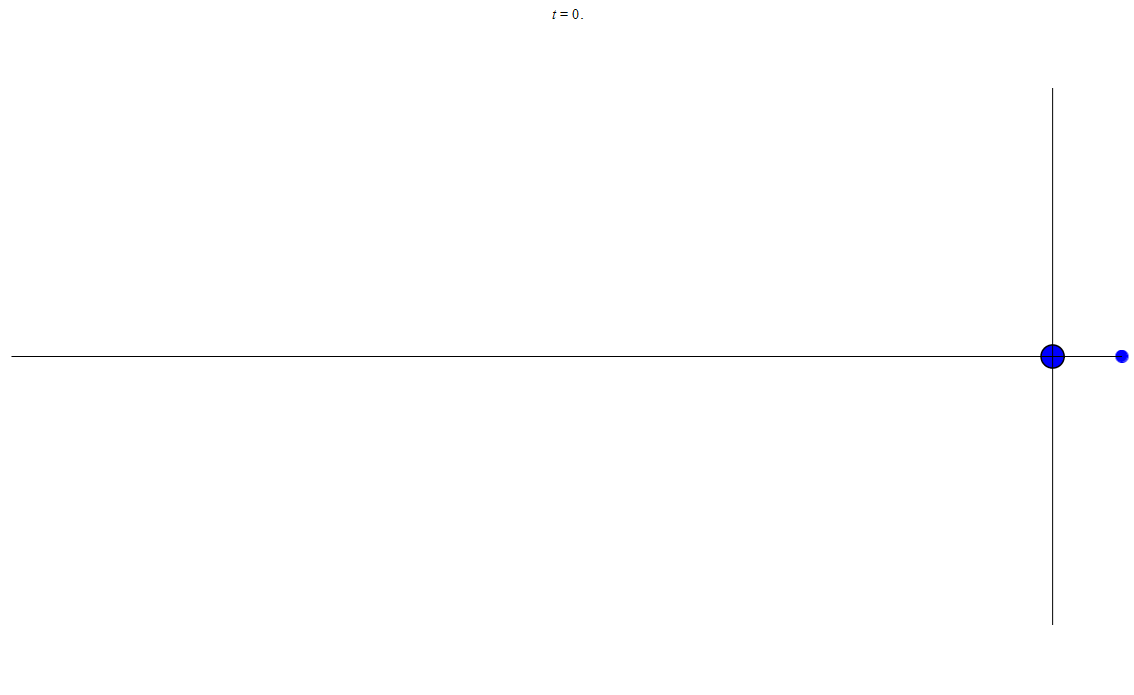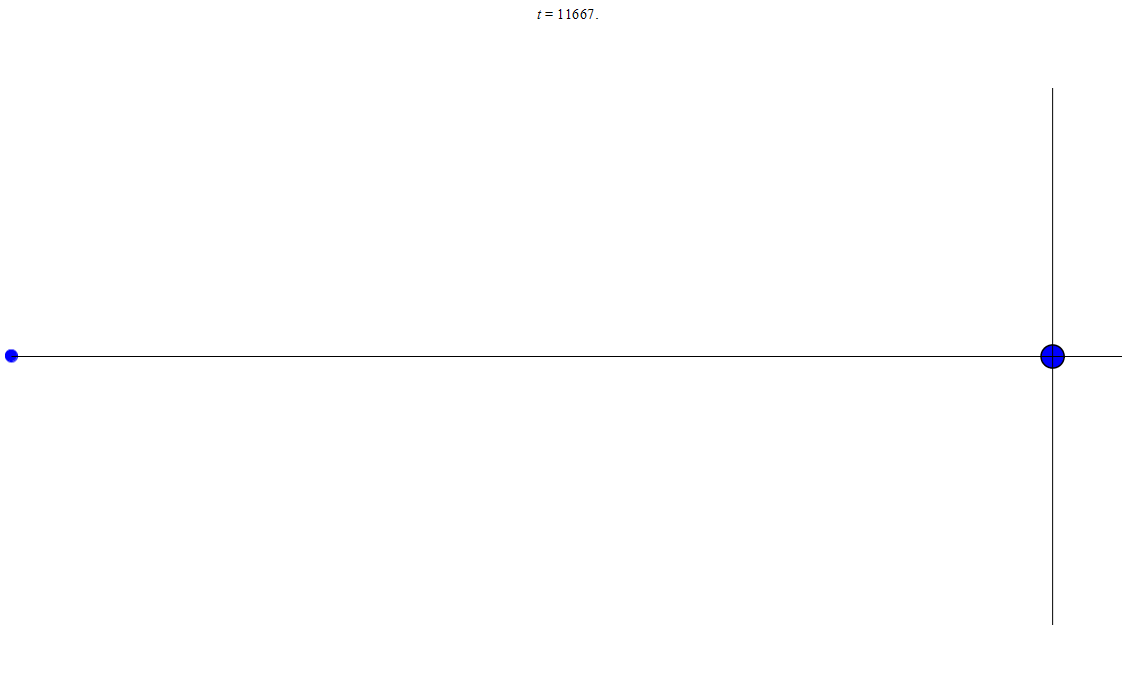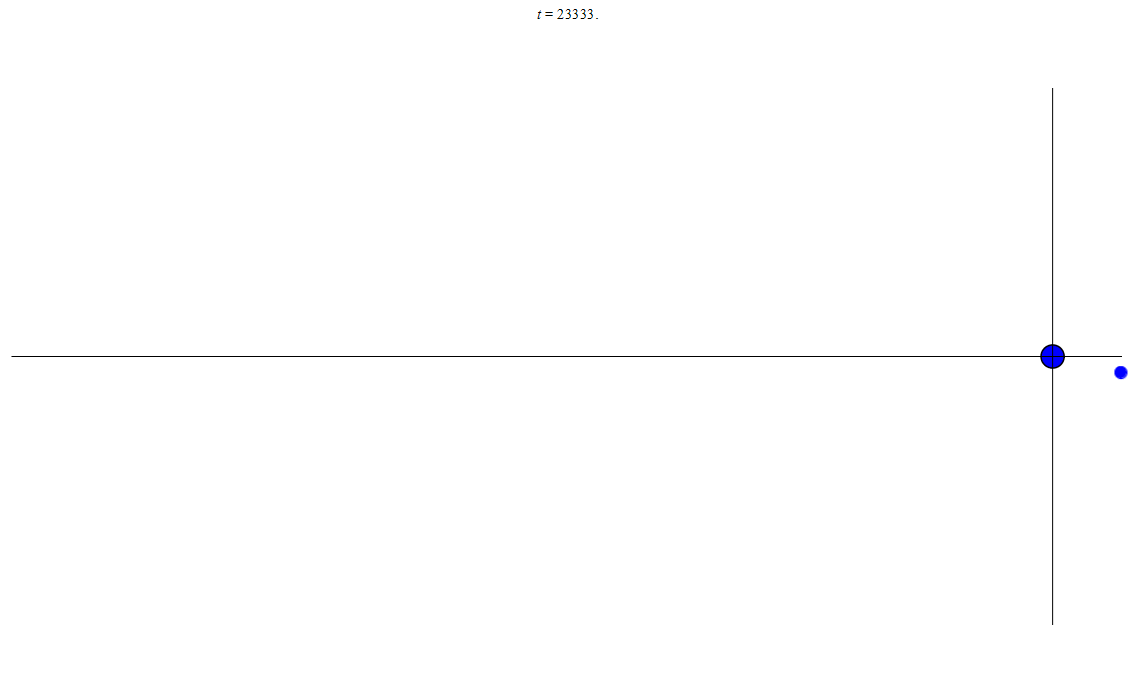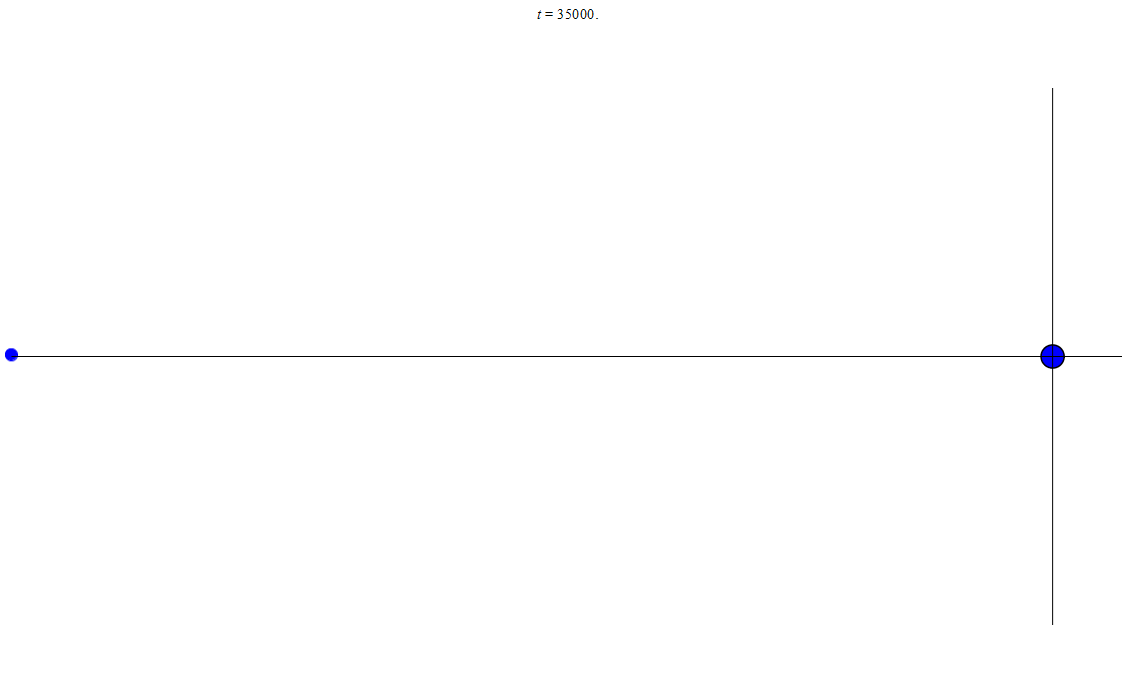
анимация 1: спутник летает по эллипсу

Из этих всех картинок и анимаций видно, что если уж и получается «эллипс», то он как-то расположен сбоку. В смысле центр эллипса не совпадает с началом координат. А всегда смещен вбок. А еще можно заметить, что тело движется неравномерно. Чем ближе к началу координат (или массивному неподвижному телу) — тем быстрее летит. Величина скорости от времени:

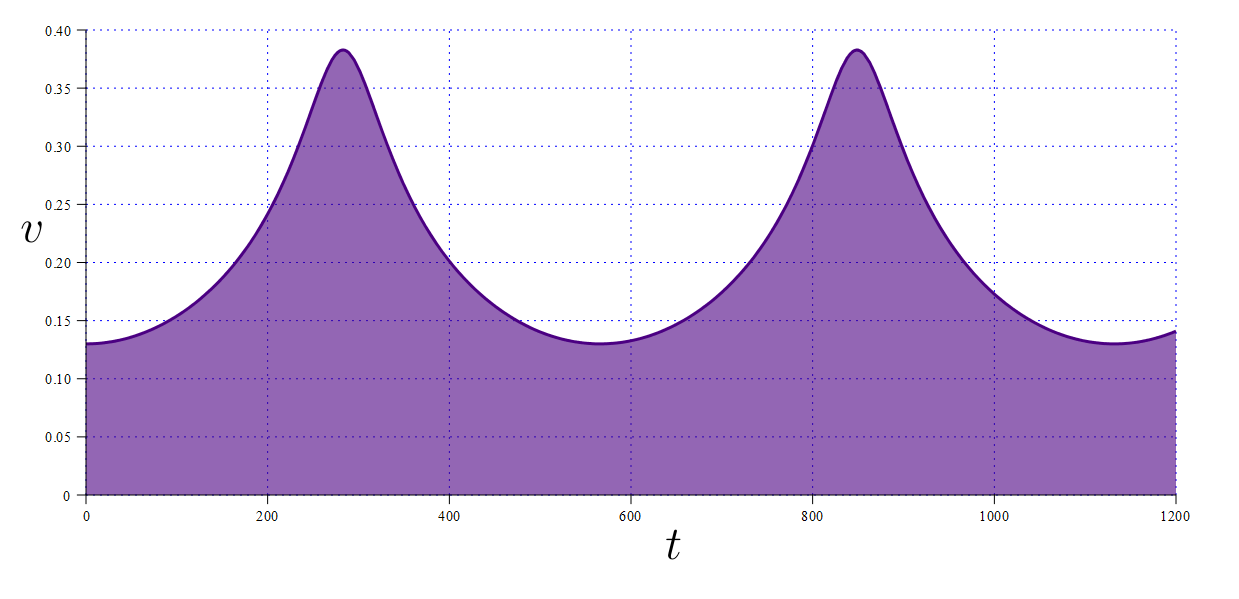
Скорость спутника

Ладненько, будем решать систему уравнений. Если сразу не решается, то бишь уравнение не напоминает ничего стандартного, уже решенного. Тогда применяют замену переменных — стандартный приём. Учитывая, что у нас получаются замкнутые овальные фигуры, а иногда даже круги, можно попробовать перейти в полярные координаты. Но это не главный аргумент приводящий к этому решению. Главный же, вот:

$x^{2}+y^{2}$

Эта штука сидит в правых частях обеих уравнений в знаменателе. Еще и под корнем. А сам корень в третьей степени.

Полярные координаты это вот что такое. Хотя объяснять не буду, просто покажу:

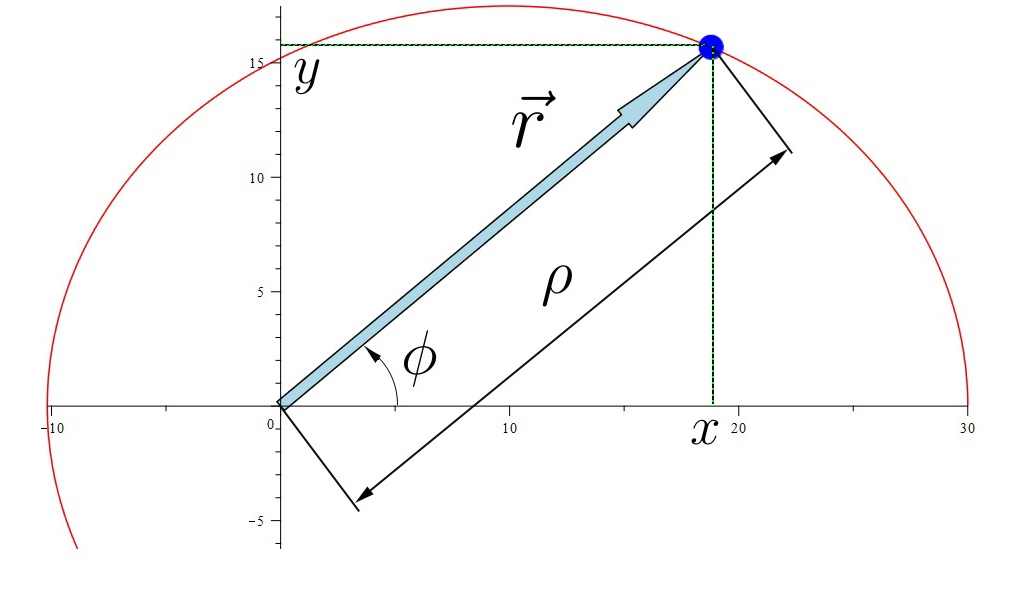
Полярная система координат

Связь между старыми и новыми переменными легко установить, школьная тригонометрия:
\begin{equation*}
\begin{cases}
x = \rho\cos (\phi),
\\
y = \rho\sin (\phi).
\end{cases}
\end{equation*}
Если возвести в квадрат оба уравнения и сложить, будет:

$x^{2} + y^{2} = \rho^{2}\cos^{2}(\phi) + \rho^{2}\sin^{2}(\phi) = \rho^{2}[\cos^{2}(\phi) + \sin^{2}(\phi)],$

$\rho^{2} = x^{2} + y^{2}.$

Ах вот зачем использовать полярные координаты, тогда ведь наши дифференциальные уравнения приобретут вид (для начала хотя бы правые части):
\begin{equation*}
\begin{cases}
\ddot{x} = -\mu \dfrac{x}{(x^{2}+y^{2})^{\frac{3}{2}}} = -\mu \dfrac{\rho\cos (\phi)}{(\rho^{2})^{\frac{3}{2}}},
\\
\ddot{y} = -\mu \dfrac{y}{(x^{2}+y^{2})^{\frac{3}{2}}} = -\mu \dfrac{\rho\sin (\phi)}{(\rho^{2})^{\frac{3}{2}}},
\end{cases}
\end{equation*}
и сокращая на $\rho$ числитель и знаменатель:
\begin{equation*}
\begin{cases}
\ddot{x} = -\mu \dfrac{\cos (\phi)}{\rho^{2}},
\\
\ddot{y} = -\mu \dfrac{\sin (\phi)}{\rho^{2}}.
\end{cases}
\end{equation*}
Не ну, явно приятней смотреть. А что делать с левыми частями? Очевидно нужно продифференцировать. Не стоит забывать: $\left\lbrace \rho(t), \phi(t) \right\rbrace$ — функции времени, это наши новые переменные вместо $\left\lbrace x(t), y(t)\right\rbrace$ . Задачка двумерная, и переменных должно быть две. Два было — два стало.

Легким дифференцированием руки, наши уравнения превращаются…уравнения превращаются…

\begin{equation*}
\begin{cases}
x = \rho\cos (\phi)
\\
y = \rho\sin (\phi)
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\dot{x} = \dot{\rho}\cos (\phi) — \rho\sin (\phi)\dot{\phi}
\\
\dot{y} = \dot{\rho}\sin (\phi) + \rho\cos (\phi)\dot{\phi}
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\ddot{x} = \ddot{\rho}\cos (\phi) — 2\dot{\rho}\dot{\phi}\sin (\phi) — \rho\ddot{\phi}\sin (\phi) — \rho\dot{\phi}^{2}\cos (\phi)
\\
\ddot{y} = \ddot{\rho}\sin (\phi) + 2\dot{\rho}\dot{\phi}\cos (\phi) + \rho\ddot{\phi}\cos (\phi) — \rho\dot{\phi}^{2}\sin (\phi)
\end{cases}
\end{equation*}

Вот в это:
\begin{equation*}
\begin{cases}
\ddot{\rho}\cos (\phi) — 2\dot{\rho}\dot{\phi}\sin (\phi) — \rho\ddot{\phi}\sin (\phi) — \rho\dot{\phi}^{2}\cos (\phi) = -\mu \dfrac{\cos (\phi)}{\rho^{2}}
\\
\ddot{\rho}\sin (\phi) + 2\dot{\rho}\dot{\phi}\cos (\phi) + \rho\ddot{\phi}\cos (\phi) — \rho\dot{\phi}^{2}\sin (\phi) = -\mu \dfrac{\sin (\phi)}{\rho^{2}}
\end{cases}
\end{equation*}
Что это? Это проще? — Минуточку!

Еще пару движений кистью и…

\begin{equation*}
\begin{cases}
\ddot{\rho}\cos (\phi) — \ddot{\phi}\rho\sin (\phi) = -\mu \dfrac{\cos (\phi)}{\rho^{2}} + 2\dot{\rho}\dot{\phi}\sin (\phi) + \rho\dot{\phi}^{2}\cos (\phi) = a
\\
\ddot{\rho}\sin (\phi) + \ddot{\phi}\rho\cos (\phi) = -\mu \dfrac{\sin (\phi)}{\rho^{2}} — 2\dot{\rho}\dot{\phi}\cos (\phi) + \rho\dot{\phi}^{2}\sin (\phi) = b
\end{cases}
\end{equation*}
(за a и b обозначили правые части, для удобства)

$\begin{bmatrix} \cos(\phi) & -\rho\sin(\phi) \\ \sin(\phi) & \rho\cos(\phi) \end{bmatrix} \begin{bmatrix} \ddot{\rho} \\ \ddot{\phi} \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix}$

Применяем метод Крамера для решения этой штуки:

$\begin{vmatrix} \cos(\phi) & -\rho\sin(\phi) \\ \sin(\phi) & \rho\cos(\phi) \end{vmatrix} = \rho\cos^{2}(\phi) + \rho\sin^{2}(\phi) = \rho$

\begin{equation*}
\begin{cases}
\ddot{\rho} = \dfrac{1}{\rho}\begin{vmatrix}
a & -\rho\sin (\phi) \\
b & \rho\cos (\phi)
\end{vmatrix} = \dfrac{1}{\rho}\left[ a\rho\cos (\phi) + b\rho\sin (\phi)\right] = a\cos (\phi) + b\sin (\phi) \\
\ddot{\phi} = \dfrac{1}{\rho}\begin{vmatrix}
\cos (\phi) & a \\
\sin (\phi) & b
\end{vmatrix} = \dfrac{1}{\rho}\left[ b\cos (\phi) — a\sin (\phi)\right]
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\ddot{\rho} = \left (-\mu \dfrac{\cos (\phi)}{\rho^{2}} + 2\dot{\rho}\dot{\phi}\sin (\phi) + \rho\dot{\phi}^{2}\cos (\phi) \right) \cos (\phi) +\\+ \left (-\mu \dfrac{\sin (\phi)}{\rho^{2}} — 2\dot{\rho}\dot{\phi}\cos (\phi) + \rho\dot{\phi}^{2}\sin (\phi) \right) \sin (\phi) \\
\ddot{\phi} = \dfrac{1}{\rho}\left (-\mu \dfrac{\sin (\phi)}{\rho^{2}} — 2\dot{\rho}\dot{\phi}\cos (\phi) + \rho\dot{\phi}^{2}\sin (\phi) \right) \cos (\phi) — \\
— \dfrac{1}{\rho}\left (-\mu \dfrac{\cos (\phi)}{\rho^{2}} + 2\dot{\rho}\dot{\phi}\sin (\phi) + \rho\dot{\phi}^{2}\cos (\phi) \right) \sin (\phi)
\end{cases}
\end{equation*}
=) Доверься Богу и увидишь настоящие чудеса. Еще чуть-чуть; евреи 40 лет ходили по пустыне (кругами, а может даже эллипсами), а вы не можете 1 минуту подождать:
\begin{equation*}
\begin{cases}
\ddot{\rho} = -\dashuline{\mu \dfrac{\cos^{2}(\phi)}{\rho^{2}}} + \cancel{2\dot{\rho}\dot{\phi}\sin (\phi)\cos (\phi)} + \uwave{\rho\dot{\phi}^{2}\cos^{2}(\phi)} — \\ -\dashuline{\mu \dfrac{\sin^{2}(\phi)}{\rho^{2}}} — \cancel{2\dot{\rho}\dot{\phi}\sin (\phi)\cos (\phi)} + \uwave{\rho\dot{\phi}^{2}\sin^{2}(\phi)} \\
\ddot{\phi} = \dfrac{1}{\rho}\left (-\cancel{\mu \dfrac{\sin (\phi)\cos (\phi)}{\rho^{2}}} — \uwave{2\dot{\rho}\dot{\phi}\cos^{2}(\phi)} + \xcancel{\rho\dot{\phi}^{2}\sin (\phi)\cos (\phi)} \right) — \\
— \dfrac{1}{\rho}\left (-\cancel{\mu \dfrac{\sin (\phi)\cos (\phi)}{\rho^{2}}} + \uwave{2\dot{\rho}\dot{\phi}\sin^{2}(\phi)} + \xcancel{\rho\dot{\phi}^{2}\sin (\phi)\cos (\phi)} \right)
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\ddot{\rho} = -\dfrac{\mu}{\rho^{2}}[\sin^{2}(\phi) + \cos^{2}(\phi) ] + \rho\dot{\phi}^{2}[\sin^{2}(\phi) + \cos^{2}(\phi) ] \\
\ddot{\phi} = -\dfrac{2\dot{\rho}\dot{\phi}}{\rho}[\sin^{2}(\phi) + \cos^{2}(\phi) ]
\end{cases}
\end{equation*}

и получается совсем неплохо:
\begin{equation*}
\begin{cases}
\ddot{\rho} = -\dfrac{\mu}{\rho^{2}} + \rho\dot{\phi}^{2} \\
\ddot{\phi} = -\dfrac{2\dot{\rho}\dot{\phi}}{\rho}
\end{cases}
\end{equation*}
Так что не нужно роптать раньше времени, Бог всегда ведет нас правильным путем. Всегда.

Ну ка, взглянем повнимательней на второе равенство:

$\dfrac{d\dot{\phi}}{\cancel{dt}} = -\dfrac{2\dot{\phi}}{\rho}\dfrac{d\rho}{\cancel{dt}}$

Есть возможность немножко проинтегрировать:

$\dfrac{d\dot{\phi}}{\dot{\phi}} = -2\dfrac{d\rho}{\rho}$

$\int\dfrac{d\dot{\phi}}{\dot{\phi}} = -2\int\dfrac{d\rho}{\rho}$

Элементарные интегралы, и константу не забываем:

$\ln{\dot{\phi}} = -2\ln{\rho} + \ln{h}$

Элементарные школьные преобразования:

$\ln{\dot{\phi}} + \ln{\rho^{2}} = \ln{h}$

$\ln{\dot{\phi}\rho^{2}} = \ln{h}$

$\dot{\phi}\rho^{2} = h$

Не, не так. Вот так:

$h = \rho^{2}\dot{\phi}$

Вы скажете: ну почему мы константу в виде логарифма записали — понятно. Но почему у нас константа — $ h $ ? Константы всегда — $ C $ !

А я отвечу народу:

Иегова Бог говорит так: вспомни, Израиль, о моменте импульса, который ты получил в прошлой статье:

$\vec{h} = [\vec{r}, \dot{\vec{r}}]$

Так, но мы ведь уже в новой координатной системе. В ней вектора $\vec{h}, \vec{r}$ будут иметь такие компоненты:

$\vec{h} = (0, 0, h)$

$\vec{r} = (x, y, 0)$

Как и договаривались ранее — штрихи не пишем. А вектор $\vec{h}$ перпендикулярен к плоскости вращения, естественно у него будет только одна компонента, причем равна его длине. Вектор $\vec{r}$ наоборот — лежит в этой плоскости и компонент две.

А вот теперь, если еще добавить полярную систему координат, в которой мы теперь работаем, можно интересно поупражняться:

$\vec{r} = \left[ \rho\cos(\phi), \rho\sin(\phi), 0\right]$

$\dot{\vec{r}} = \left[ \dot{\rho}\cos(\phi) - \rho\sin(\phi)\dot{\phi}, \dot{\rho}\sin(\phi) + \rho\cos(\phi)\dot{\phi}, 0 \right]$

И тогда должно получится нечто явно интересное:

$h\vec{k} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ \rho\cos(\phi) & \rho\sin(\phi) & 0 \\ \dot{\rho}\cos(\phi) - \rho\sin(\phi)\dot{\phi} & \dot{\rho}\sin(\phi) + \rho\cos(\phi)\dot{\phi} & 0 \end{vmatrix} =$

$= 0\vec{i} + 0\vec{j} + \begin{vmatrix} \rho\cos(\phi) & \rho\sin(\phi) \\ \dot{\rho}\cos(\phi) - \rho\sin(\phi)\dot{\phi} & \dot{\rho}\sin(\phi) + \rho\cos(\phi)\dot{\phi} \end{vmatrix}\vec{k}$

Очевидно:

$h = \rho\cos(\phi)\left( \dot{\rho}\sin(\phi) + \rho\cos(\phi)\dot{\phi} \right) - \rho\sin(\phi) \left( \dot{\rho}\cos(\phi) - \rho\sin(\phi)\dot{\phi} \right) =$

$= \xcancel{\rho\dot{\rho}\sin(\phi)\cos(\phi)} + \rho^{2}\dot{\phi}\cos^{2}(\phi) - \xcancel{\rho\dot{\rho}\sin(\phi)\cos(\phi)} + \rho^{2}\dot{\phi}\sin^{2}(\phi) =$

$= \rho^{2}\dot{\phi}[\sin^{2}(\phi) + \cos^{2}(\phi) ] = \rho^{2}\dot{\phi}$

А нука теперь сравним полученные нами равенства:
\begin{equation*}
\begin{cases}
h = \rho^{2}\dot{\phi} \\
h = \rho^{2}\dot{\phi}
\end{cases}
\end{equation*}
Вот такое вот совпадение.
Ок, давайте пристально рассмотрим, что же это выражение может значить. Всё таки нам Бог пророчества давал о нём, оно явно важно. А также, не много, ни мало — это один из первых интегралов нашей системы.

Модуль векторного произведения $ h $ — суть площадь параллелограмма натянутого на вектора в скобках $[\vec{r}, \dot{\vec{r}}]$ . Площадь…

Постойте-ка, а какая размерность $\rho^{2}\dot{\phi}$ :

$\text{м}^{2}\cdot\dfrac{\text{рад}}{c} = \dfrac{\text{м}^{2}}{c}$

Метры в квадрате деленные на секунду. Площадь за единицу времени… Площадь, полярные координаты, время; Боже дай нам понять что это!

А, загуглим ка площадь в полярных координатах, давно это было на первом курсе, начала матана:

$S = \dfrac{1}{2}\int\rho^{2}d\phi$

Всё ясно ( $ h $ константа, не забываем):

$\rho^{2}\dot{\phi} = \rho^{2}\dfrac{d\phi}{dt} = h,$

$\rho^{2}d\phi = hdt,$

$\int\rho^{2}d\phi = h\int dt = ht + C,$

Тогда площадь:

$S = \dfrac{1}{2}(ht + C)$

Ну еще одна константа $ C $ — это в принципе начальная площадь, или её половина, точнее две. Пускай в нулевой момент времени площади у нас будет 0:

$S = \dfrac{ht}{2}$

или же скорость изменения площади — постоянна:

$\dot{S} = \dfrac{h}{2}$

Красиво получается — площадь растет линейно. Равномерно. Хотя тело движется, как мы видели — совсем не равномерно. Особенно когда по эллипсу. Ну это логично, потому что площадь у нас (в полярных координатах) выходит «заметанием» радиуса вектора: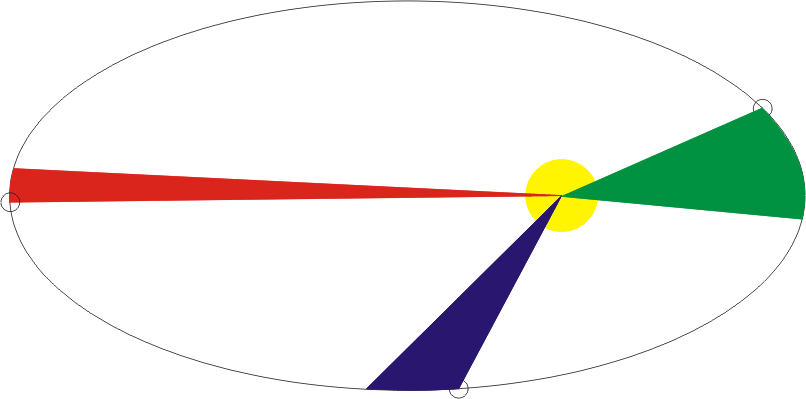

За равные промежутки времени получаются равные площади, красивая картинка из Википедии

И поэтому телу нужно лететь тем быстрее, чем ближе к центру вращения, и тем медленнее, чем дальше. Только тогда наши «треугольники» будут иметь равные площади.

И может быть кто-то не поверит, но мы с вами только что, лишь с помощью ручки, бумажки и матана открыли Второй закон Кеплера. Это один из трех законов открытых эмпирически, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Сделал он (Иоганн) это около 1607 года и звучит он так:

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, заметает собой равные площади.

И вы не поверите, может быть, но второй закон был открыт Кеплером раньше первого. Как и у нас. Но он сделал это эмпирически.

Ох, слишком много совпадений… Еще и Ньютон со своими законами, тоже второй его закон немного главнее первого, и оный вытекает из второго.

А вот что Кеплер говорил о астрономии и астрологии:

Конечно, эта астрология глупая дочка; но, Боже мой, куда бы делась её мать, высокомудрая астрономия, если бы у неё не было глупенькой дочки! Свет ведь ещё гораздо глупее и так глуп, что для пользы этой старой разумной матери глупая дочь должна болтать и лгать. И жалованье математиков так ничтожно, что мать наверное бы голодала, если бы дочь ничего не зарабатывала.

Кеплер понимал Бога, понимал единство мира. А Бог евреям тоже говорил за 3000 лет до этого, что астрология — ху*ня. Чревовещание — ху*ня. Всё ху*ня, Миша, занимайтесь наукой. И почему так верунов не любят современные дети. Всё просто — в Библию никто не заглядывает.

Но пойдем дальше. Хотите услышать как звучит первый закон Кепелера?

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Можно сказать, что мы частично открыли и первый: знаем, что тело вращается в неизменной плоскости (а эллипс по определению — плоская кривая), но пока, к сожалению, еще не знаем, что это «эллипс». И что его «фокус» находится как раз в центре координат. Всё будет, но позже, и про конические сечения поговорим, и про эллипсы, и про их фокусы.

Сейчас будем заканчивать, но перед этим я закину крючок, извините вам в рот, за щеку:

$\rho^{2}\dot{\phi} = h$

$\dot{\phi} = \dfrac{h}{\rho^{2}}$

А теперь фокус-покус (это первое уравнение из нашей системы):

$\ddot{\rho} = -\dfrac{\mu}{\rho^{2}} + \rho\dot{\phi}^{2}$

$\ddot{\rho} = -\dfrac{\mu}{\rho^{2}} + \rho\left( \dfrac{h}{\rho^{2}} \right)^{2}$

Вуаля!

$\ddot{\rho} = -\dfrac{\mu}{\rho^{2}} + \dfrac{h^{2}}{\rho^{3}}$

Не, ну это уже можно пытаться решить, красиво. В следующем посте продолжим решать…

хлеб наш насущный дай нам на сей день.

PayPal ($): what.is.truth.19@gmail.com
Bitcoin (BTC): 1AodAFYCbwrwTiZb5JVsQjv37G5toBcyQ
Ethereum Classic (ETC): 0×9234016395e0e6ef7cf6c0aa0f6f48f91ab39239
Ripple (XRP): rLW9gnQo7BQhU6igk5keqYnH3TVrCxGRzm (адрес), 270547561 (тег)
Bitcoin Cash (BCH): bitcoincash: qzxfz2hdcl0hv23a3hlcefsy07mglssjtgwrckhyg8

или webmoney (Ниже: Поддержать автора → Отправить деньги)

Вот приношения, которые вы должны принимать от них: золото и серебро и медь,
и шерсть голубую, пурпуровую и червленую, и виссон, и козью,
и кожи бараньи красные, и кожи синие, и дерева ситтим,
елей для светильника, ароматы для елея помазания и для благовонного курения,
камень оникс и камни вставные для ефода и для наперсника.
Исход 25

P.S.: Печально, что на Хабре нет модуля \usepackage{cancel}, но может появится, я не буду некоторые формулы пока исправлять. Или это в mathjax нету модуля, я не разбираюсь, тогда претензии к mathjax