Проектируем космическую ракету с нуля. Часть 3 — Ужепочти-решение задачи двух тел
Содержание
Часть 1 — Задача двух тел
Часть 2 — Полу-решение задачи двух тел
Движение в плоскости
Осталось сделать последний штрих. Решить это уравнение:
где — относительное расстояние между телами.
В прошлом выпуске было показано, что при значительном различии масс (например можно считать радиусом вектором в новой системе координат связанной с неподвижным массивным телом. Неподвижное оно потому, что центр масс совпадает с ним, а центр масс движется равномерно прямолинейно (тоже в прошлом выпуске доказали).
Но всё это лишь для удобства восприятия нами. Предельный случай, когда массивное тело неподвижно и сосредоточено в начале системы координат, а второе легкое тело вращается вокруг, прямо как спутник на орбите Земли. А как раз описывает траекторию движения спутника.
Земля конечно не движется равномерно и прямолинейно и тем более не является неподвижной находящейся в центре Вселенной (хотя это наша воля назначить центр). Да и точкой не является, по крайней мере в примере со спутником.
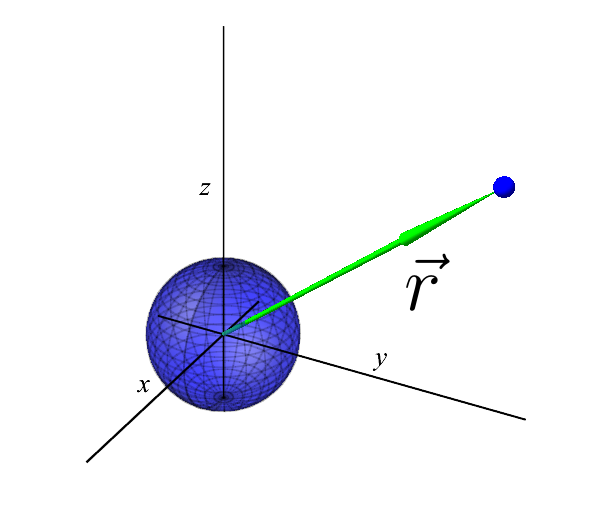
Земля и спутник
Но всё таки, если непродолжительное время понаблюдать за Землей со стороны, то нам будет казаться, что она (Земля) пролетела в космосе по прямой, причем равномерно. Вот вы чувствуете центростремительное ускорение вызываемое вращением Земли вокруг Солнца? И я нет. Мы даже не чувствуем (вестибулярным аппаратом), что она (Земля) вращается вокруг своей оси. И сила Кориолиса практически не проявляется. Так может Земля — плоская? Лично я не проверял : D Но давайте будем верить официальной науке, что всё это благодаря масштабам. Вот если взять сделать центрифугу в космосе для создания искусственной гравитации, то по простым расчетам диаметр (или радиус?) должен быть не меньше километра для более менее комфортного жилья. Ибо сила Кориолиса будет создавать непривычные эффекты: бросишь мячик прямо — он улетит куда-то в сторону. Да просто ходить будет неудобно. Станешь вечно пьяным, вечно молодым испытывать непривычные ощущения, как во сне, как в сказке.
А на счёт того, что Земля представлена точкой — тоже довольно близко к правде. Так как объекты в форме шара создают вокруг себя гравитационное поле, как если бы мы сжали всю массу до точки и сконцентрировали её в центре шара. Это мы потом математически докажем, но сейчас и интуитивно, думаю, понятно. Ведь шар абсолютно симметричен. В реальности конечно же если сжать Землю до 1 см в диаметре — она станет черным отверстием. Хотя всё таки черной дырой, извиняюсь — инженерная привычка (у инженеров не бывает дыр, — только отверстия). Все инженера это знают, ибо работает хорошо эволюционный отбор: если начинающий инженер скажет на отверстие «ДЫРКА» в присутствии более опытного инженера, — сразу получит подзатыльник в лучшем случае. В худшем нужно ждать вертуху в щи (шутка).
Отверстие и дырка
Перед тем как решать полезно бывает сначала численно по-моделировать, возможно, это позволит заметить какие-то закономерности. Уравнения уже попроще, чем в прошлый раз:
\begin{equation*}
\begin{cases}
\ddot{x} = -\mu \dfrac{x}{(x^{2}+y^{2}+z^{2})^{\frac{3}{2}}},
\\
\ddot{y} = -\mu \dfrac{y}{(x^{2}+y^{2}+z^{2})^{\frac{3}{2}}},
\\
\ddot{z} = -\mu \dfrac{z}{(x^{2}+y^{2}+z^{2})^{\frac{3}{2}}}.
\end{cases}
\end{equation*}
Берем и вбиваем это куда-нибудь, что умеет решать. В мат-пакет, либо прямо в Python:) Я в Python не стану вбивать, хотя могу. Это потому что мне 3d визуализация matplotlib не нравится. Плюс еще с сохранением gif-ок всё не очень просто, было начал искать — нашел лишь сохранение в видео-формате, так еще и устанавливать дополнительно всякого го*на нужно.
Вот и повод поинтересоваться у аудитории Хабра: можно ли делать подобные 3d анимации как в этой статье, но в matplotlib? Чтобы перспектива была такая красивая (там где я делаю — можно перспективу регулировать). Или посоветуйте какие классные библиотеки Python для визуализации, буду благодарен.
Короче вот несколько вариантов с разными начальными условиями:
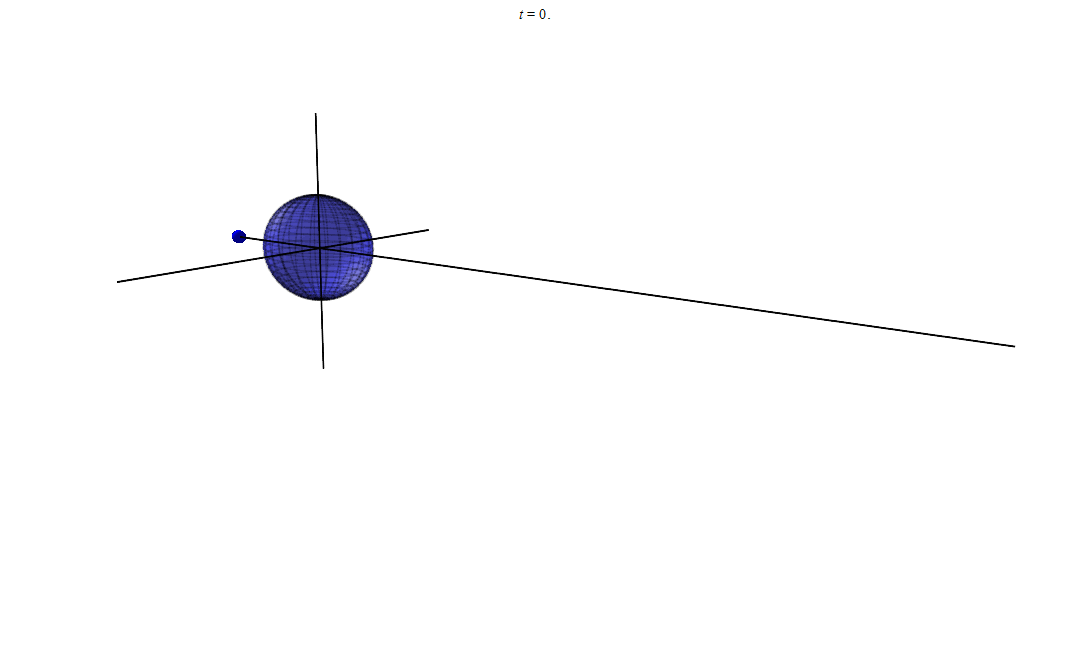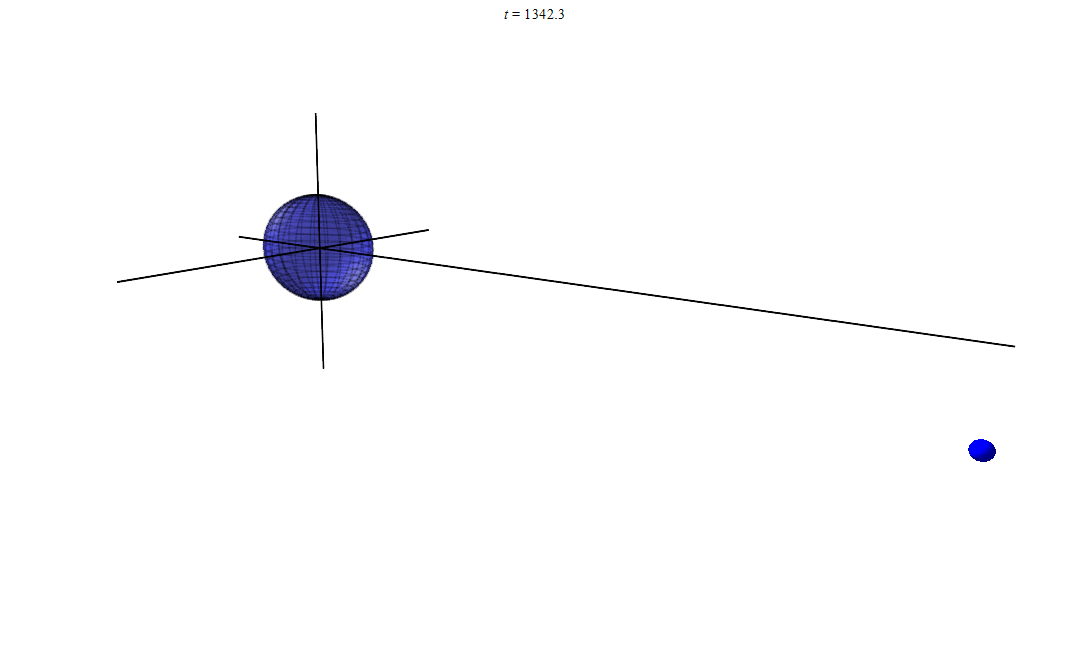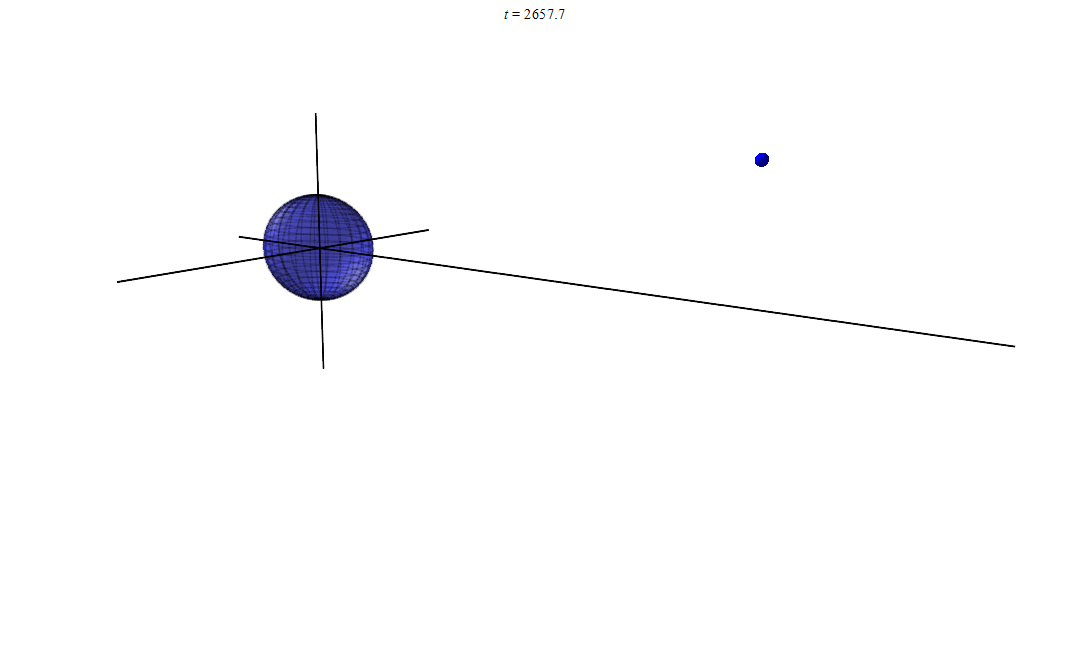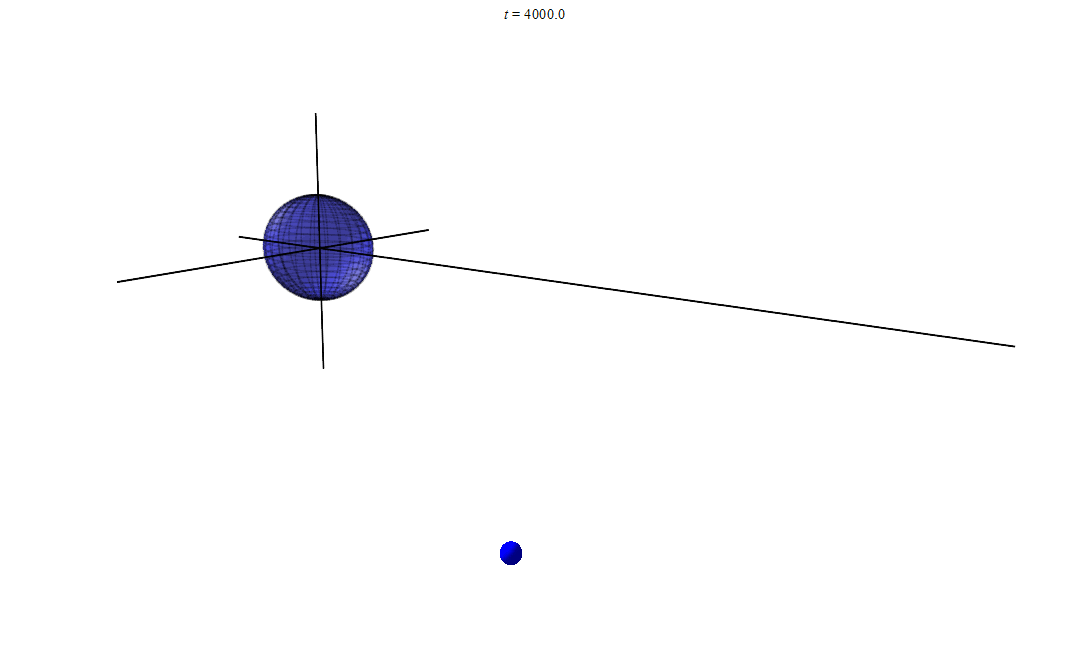
анимация 1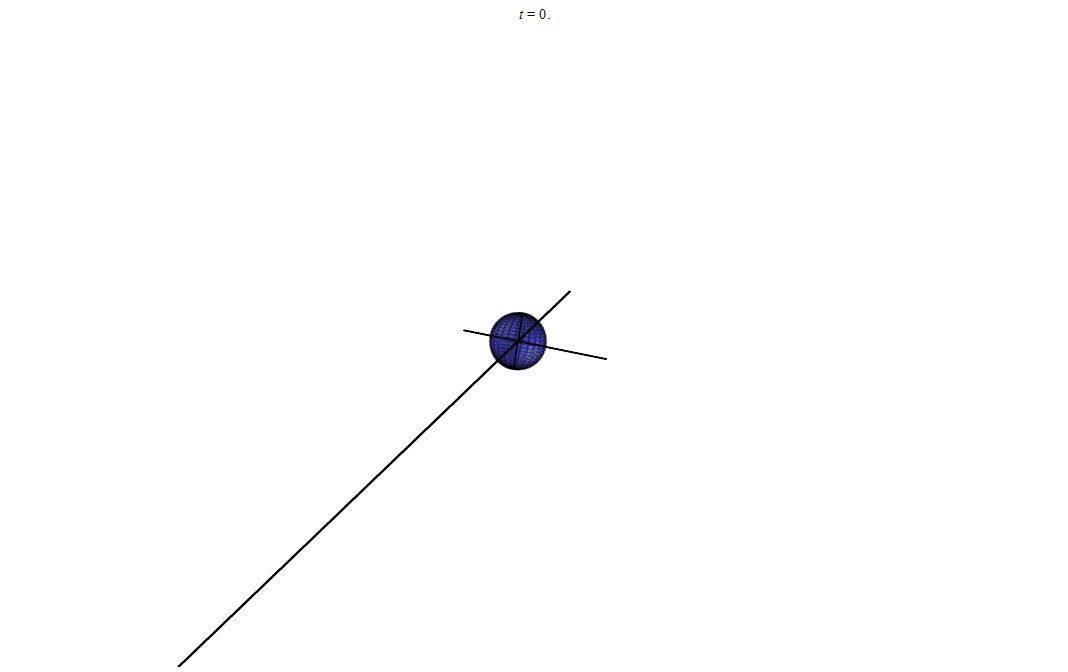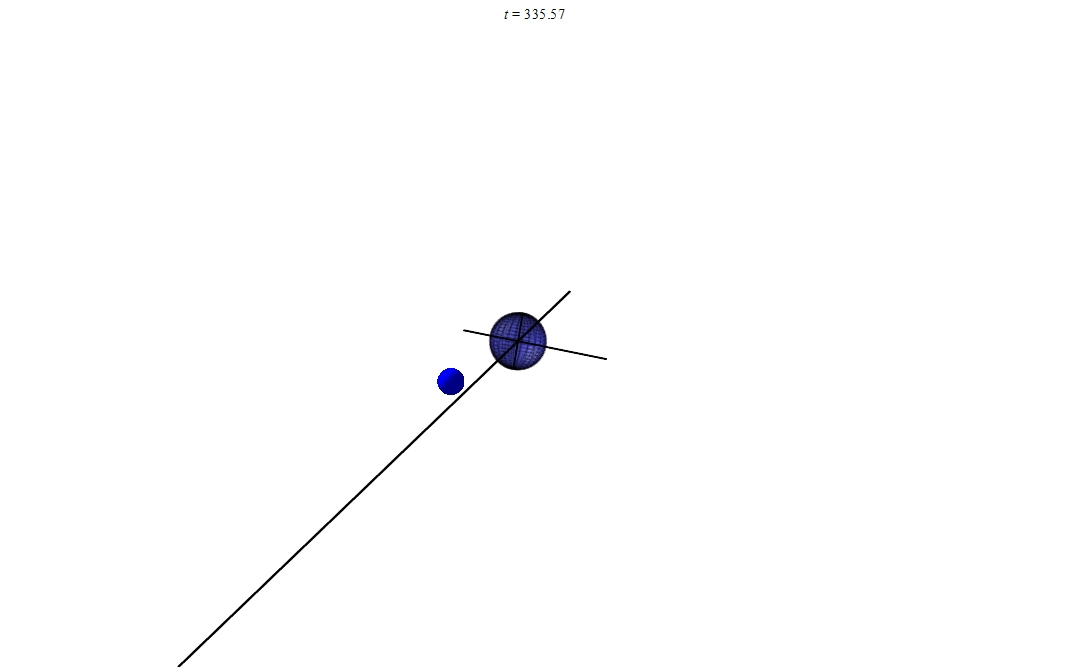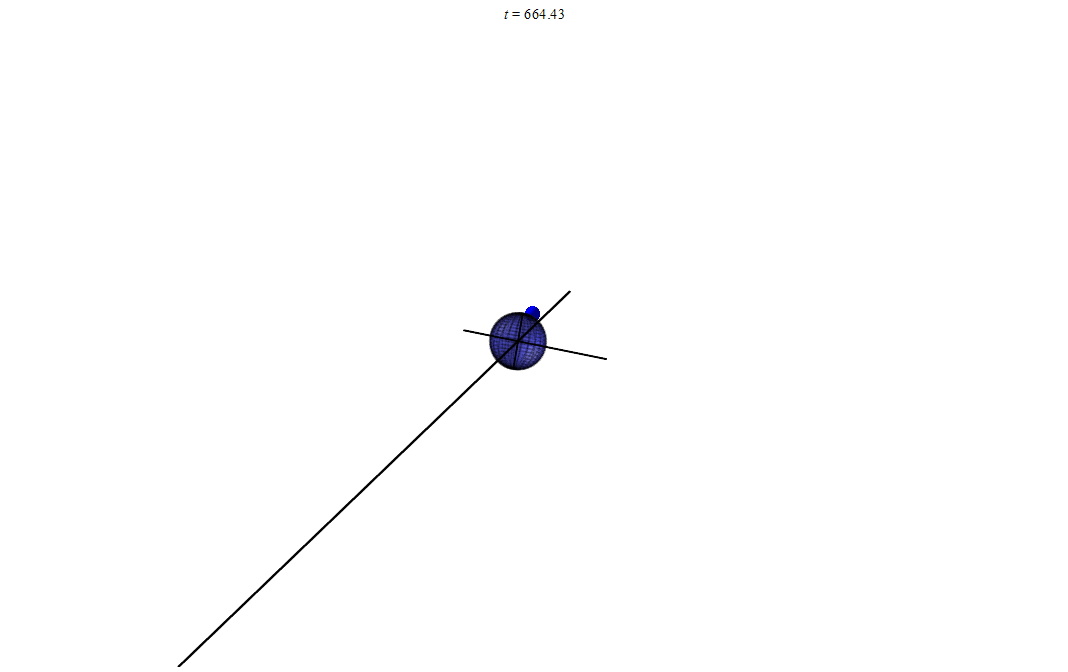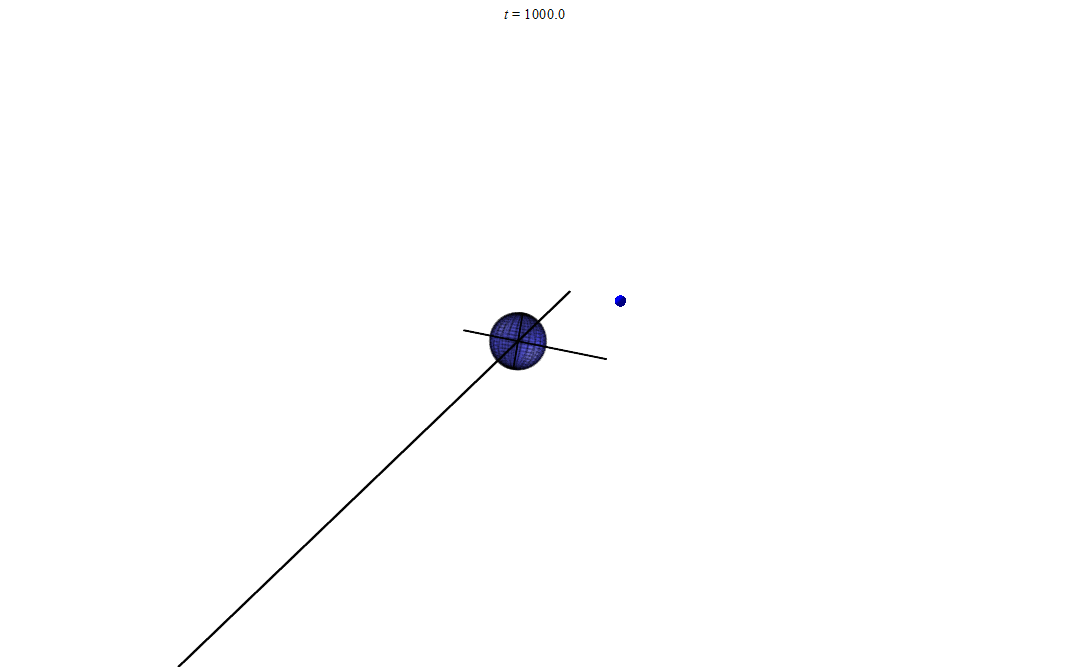
анимация 2
анимация 3
Если еще 10–100 раз смоделировать, то наверняка мы заметим, что маленький шарик движется всегда в одной плоскости. И эту плоскость можно вычислить, имея начальные условия. Ведь радиус вектор всегда лежит в этой плоскости, но и скорость
лежит в ней же. А если всегда, то и в начальный момент времени. Значит мы в состоянии вычислить эту плоскость.
В данном случае удобно задавать плоскость с помощью вектора нормали и любой точки лежащей в ней. Точки у нас аж две — начало системы координат и начальное положение спутника, выбирай любую — выберем начало . А вектор нормали легко получить векторно умножив вот это:
где .
назовём кинетическим моментом системы. Потому что похож на момент импульса:
Можно даже назвать кинетический момент — удельным моментом импульса:
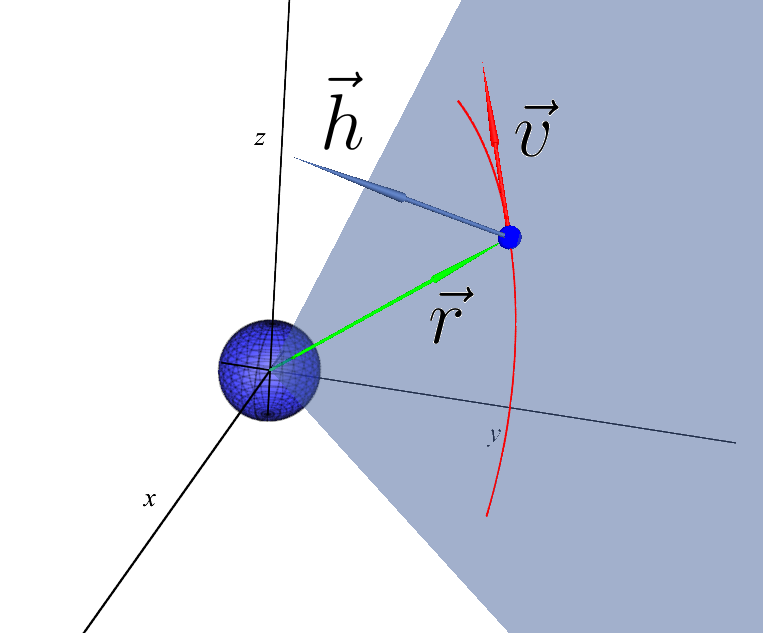
Вектор нормали
Можно ли проверить с помощью уравнений, что действительно всегда будет параллельным себе же в начальный момент времени?
Ну если это так, то для любого момента времени должно быть выполнено:
здесь — какая-то функция времени, которая регулирует длину
, ведь
в принципе может быть параллелен себе, но по длине изменяться.
Ну давайте продифференцируем это равенство, используя все правила дифференцирования векторных произведений и их свойств:
Как хорошо получается, у нас же:
ну так и подставим туда:
А это значит, что . Или же
. Короче говоря
постоянен как по направлению так и по длине. Вот и всё, закон сохранения.
Данный факт можно, конечно, было получить и без всех этих рассуждений и физических смыслов. Просто играясь с самими формулами. Брать равенство и векторно умножить его на (просто потому что справа тогда будет ноль):
учитывая:
теперь разок проинтегрировав, получаем уже полученную вектор константу:
Если — константа, то она может и нулю равняться. А такое может быть только если
и
будут параллельны. Это значит, что скорость будет направлена вдоль радиуса вектора. Именно это и происходило, когда на голову Ньютона падало яблоко.

Эх, яблочко.
В принципе, в принципе, так можно продолжать играть дальше. Например, попробовать векторно умножить имеющееся у нас уравнение на , или использовать скалярное произведение. В общем комбинировать и надеяться на лучшее. Операций у нас не так уж и много, и свойств тоже, — по пальцам пересчитать, так что не грех. На самом деле мы это и будем проделывать позже. И это даст свои плоды, даже откроет еще один способ решения задачи (получения уравнения траектории), но мы решим обеими способами, так статьи длиннее получатся =)).
А теперь продолжим. Из за того что траектория лежит в плоскости (пускай пока что как-то там в пространстве расположенной), получается задача то у нас — плоская. А это значит, что вместо трех дифференциальных уравнений второго порядка, на самом деле их два. Но в правильно выбранной системе отсчета. Например в такой:
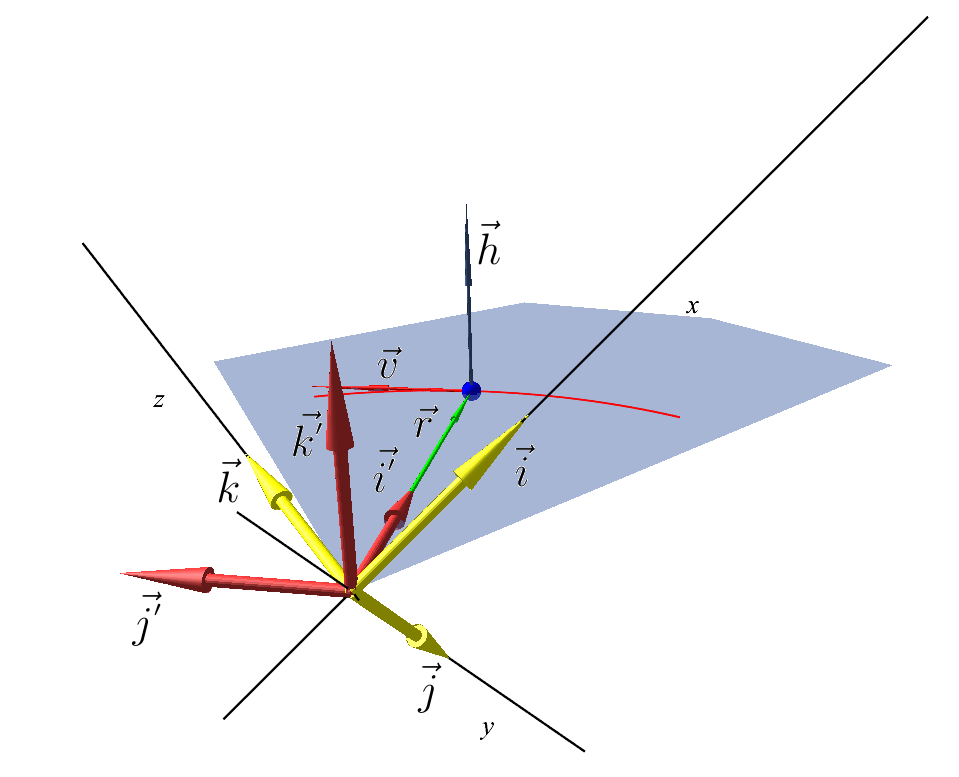
Правильная система отсчета
Новый базис связан со старым так (пишу в порядке вычисления):
Или в матричном виде:
А можно и так и сяк:)
Соответственно переход наоборот:
Любой вектор, например скорость , остается одним и тем же вектором в независимости выбранной нами системы отсчета, то бишь можно расписывать так:
Или. Же.
Хорошо статья тянется, как резиновая:
Как преобразуются базисы мы в курсе, тогда очень просто найти как преобразуются компоненты векторов при переходе (это я напоминаю аналитическую геометрию, а может кому-то что-то проясниться и мои записи станут полезными):
Ну и очевидно компоненты равны:
Транспонируем их, а то как неродные:
Это не я. Это всё правила транспонирования.
Карочь, взяли базисы подставили, туда-сюда, сравнили и всё.
Но нас ждет еще один маленький сюрприз. В хорошем смысле слова. У нас матрица поворота. А значит она — ортогональная матрица. Ортогональные матрицы имеют прикольное свойство:
Тогда переходы получаются — просто прелесть (не бесовская):
Просто бери матрицу A и переходи в новую систему координат:
Как вызывать вычислять компоненты матрицы A, надеюсь никто не провтыкал (извините за французский). Например:
Ну и хватит, пойдем дальше.
Теперь то, из-за того что точка всегда лежит в плоскости , вектор
будет иметь вид:
Координата всегда ноль.
Проще стало:
И ускорение:
Договоримся не тащить штрих, обозначающий, что мы в очередной новой системе координат, ибо он как груз на шее висит. И дальше будем писать без штриха, а еще задача теперь двумерная, на плоскости:
И уравнений будет два (уже есть):
\begin{equation*}
\begin{cases}
\ddot{x} = -\mu \dfrac{x}{(x^{2}+y^{2})^{\frac{3}{2}}},
\\
\ddot{y} = -\mu \dfrac{y}{(x^{2}+y^{2})^{\frac{3}{2}}}.
\end{cases}
\end{equation*}
Это ведь мы решаем-решаем, даст Бог решим. А потом главное вернуться поочередно в исходную систему координат. Так что забывать откуда мы пришли — нельзя. После перехода матрицы выбрасывать — нельзя. Лучше заранее найди обратную, как говорится: готовь сани летом, а тележку зимой.
Думаю на этот раз хватит, продолжение будет в следующих статьях. Которые будут длиннее.
