Проблема холодного старта персонализации новостной ленты
Сегодня мы хотели бы рассказать о своем исследовании в области персонализации новостной ленты в рамках проекта favoraim. Сама идея показывать пользователю только те новости (далее записи), которые будут ему интересны, не новая и вполне естественная. Для решения этой задачи есть устоявшиеся и хорошо зарекомендовавшие себя модели.Принцип работы этих алгоритмов похож: мы анализируем реакцию пользователей (feedback) на предыдущие записи и пытаемся прогнозировать его реакцию на текущие события. Если реакция «положительная», событие попадает в ленту, если «отрицательная» — не попадает. О том, что такое «положительная» и «отрицательная» реакция позже, а пока рассмотрим, какую же реакцию мы можем получить от пользователя: Оценка записи, например, по пятибалльной шкале.
Like/dislike, что является частным случаем первого варианта (-1, +1)
Неявная обратная связь (implicit feedback), это может быть, например, факт того, что пользователь открыл страницу данной записи; время, которое пользователь просматривал информацию о записи и т.п.
Для первого и второго случая мы можем предсказать рейтинг для события, которое пользователь еще не успел оценить, основываясь на оценках этого же события другими пользователями. Для этого мы можем использовать какую-либо корреляционную модель (например, k-nearest neighbor (kNN), где для предсказания оценки записи мы используем оценки «похожих» пользователей этой же записи), либо латентную модель, основанную на матричном разложении (например, SVD или SVD++), что более предпочтительно. В последнем случае, когда мы обладаем только данными о просмотренных записях, мы исходим из предположения, что пользователь будет просматривать интересные ему записи намного чаще, чем неинтересные и воспринимаем просмотр как положительную оценку. Здесь у нас есть только положительная обратная связь (positive-only feedback), и лучше будет воспользоваться другой моделью, например, Bayesian personalized ranking (BPR). Рассказывать про эти модели нет смысла, материалов на эту тему очень много в сети.Предсказанные оценки могут использоваться как для ранжирования записей, так и в качестве фильтра (событие «интересное» — показываем, «не интересное» — не показываем). Для фильтрации нам нужно ввести некоторое пороговое значение, выше которого мы считаем оценку положительной. Тут можно придумать сколько угодно эвристик, например, в первом случае из нашего списка реакций напрашивается средняя оценка пользователя, во втором — 0. Если же мы хотим получить обоснованное пороговое значение, мы можем воспользоваться ROC-анализом.А теперь проблема: чтобы предсказать оценку пользователя для какой-либо записи, нам нужно, чтобы кто-нибудь уже оценил эту запись, причем, лучше чтобы таких оценок было много. На практике мы будем постоянно сталкиваться с ситуацией, когда у записи не будет оценок. Очевидный пример — запись только что добавлена. Это так называемая проблема холодного старта. Об этой проблеме мы и поговорим подробнее.Очевидно, что для решения этой задачи нам нужно перестать рассматривать событие как некий черный ящик, как это делалось в предыдущем подходе. Нужно получить какие-то характеристики самой записи. Вюачестве таких характеристик мы иаем использовать «тематики» записи. Будем исходить из предположения, что пользователь ставит оценку записи исходя из того, что ему понравилась или не понравилась одна или несколько тематик данной записи. Как выделить тематики записи мы рассказывали в прошлой статье (Автоматическая расстановка поисковых тегов). Такая модель является довольно грубым приближением и можно придумать сколько угодно примеров записей с одинаковыми тематиками, на которые у пользователя будет разная реакция, однако погрешность в результате получается относительно небольшой.Про отношение пользователя к той или иной тематике у нас уже будет довольно много информации, если пользователь проявил какую-нибудь активность в системе (просмотры и оценки записей с данной тематикой, поисковые запросы с данной тематикой и т.п.). Таким образом, у нас есть некоторая информация об отношении конкретного пользователя к тематикам конкретной записи и нам надо предсказать, «интересна» ли будет данная запись пользователю или нет.Немного отвлечемся и рассмотрим пример из биологии. Нас будет интересовать упрощенная модель работы нервной клетки (рис. 1). Принцип ее работы следующий: через дендриты в ядро нервной клетки из внешней среды поступают электрические импульсы. Импульс может быть как положительный, так и отрицательный. Так же, у разных дендритов может быть разная пропускная способность, т.е. импульс, проходящий через разные дендриты, так же отличается по модулю. Ядро нейрона способно накапливать заряд. Когда заряд накапливается достаточно большой, клетка генерирует импульс, который передается по аксону. Такое поведение описывается моделью Маккалока — Питтса (рис. 2).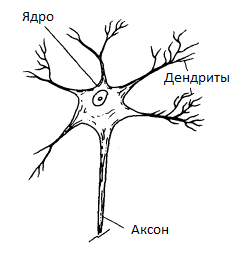
Рис. 1
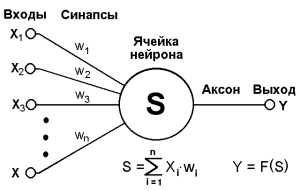Рис. 2
Теперь применим эту модель к нашей задаче. На входы нейрона будем подавать данные об отношении пользователя к тематикам события (различные оценки других событий по данным тематикам, количество поисковых запросов с данными тематиками, количество просмотров событий с данными тематиками и т.п.). Затем найдем значение S, и, если S > 0, будем считать событие «интересным». А в противном случае — «неинтересным». Эта модель также называется линейным классификатором.Все что нам осталось — определить значения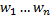 
. Этот процесс называется обучением классификатора. Принцип обучения следующий: мы берем записи, которые пользователи уже оценили (обучающая выборка), находим для каждой из них значения 
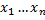и с помощью нашего классификатора пытаемся предсказать уже известную оценку для данной записи. Задача сводится к тому, чтобы отыскать значения 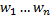, дающие наименьшее число ошибок на нашей обучающей выборке. Эта задача решается любым известным методом оптимизации. Большинство источников рекомендуют использовать для данной задачи метод стохастического градиентного спуска (SG), однако применить его «в лоб» к данной задаче не получится. Существует набор эвристик, которые все же позволяют эффективно применить данный метод для решения этой задачи, но в нашем случае использовались генетические алгоритмы, которые показались более предпочтительными для решения данной задачи на относительно небольших обучающих выборках.Генетические алгоритмы моделируют процесс естественного отбора для решения оптимизационной задачи. Принцип его работы следующий: создается популяция «особей», в генотип которых кодируются значения переменных (в нашем случае 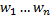). Особи популяции скрещиваются между собой и подвергаются мутации. Больший шанс «выжить» — остаться в популяции — получают те особи, которые лучше решают поставленную задачу. Данный метод обладает следующими преимуществами:
Нет необходимости выбирать начальное приближение
За счет мутации алгоритм имеет шансы не сосредотачиваться вокруг локальных минимумов.
К недостаткам можно отнести скорость работы. Для сверхбольших объемов данных стохастический градиентный спуск будет работать несравнимо быстрее. Но тут все зависит от задачи.Теперь перейдем к математической части. Нам нужно построить по обучающей выборке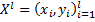 
алгоритм классификации 
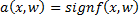с двумя классами 
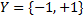, где 
— дискриминантная функция, w — вектор параметров.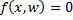 
— разделяющая поверхность. Функция имеет вид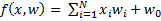 
. 
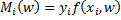— отступ (margin) объекта 
. 
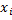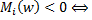алгоритм 
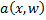ошибается на 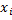.На этом месте хочется все бросить и начать обучать классификатор, минимизируя количество ошибок на обучающей выборке 
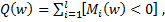однако такое решение будет не совсем корректно, т.к. в результате некоторые объекты могут находиться достаточно близко от разделяющей плоскости. Это никак не повлияет на функцию пригодности, т.к. в результате будет давать правильный результат на обучающей выборке. Однако при незначительных изменениях x, объект может изменить класс, вследствие чего на контрольной выборке у нас, скорее всего, получатся не самые лучшие результаты. В дополнение к этому, нам придется минимизировать дискретную функцию, а это весьма сомнительное удовольствие. Для решения этой проблемы мы введем невозрастающую неотрицательную функцию потерь 
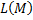и будем минимизировать функцию 
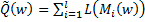, таким образом поощряя большие отступы, величину которых можно считать степенью выраженности класса. Чаще всего в качестве функции потерь используется логарифмическая функция 
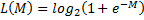, однако ей одной выбор не ограничен.Наряду с заменой функции потерь рекомендуется добавлять к функционалу Q штрафное слагаемое, запрещающее слишком большие значения нормы вектора весов 
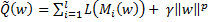. Добавление штрафного слагаемого или регуляризация снижает риск переобучения и повышает устойчивость вектора весов по отношению к малым изменениям обучающей выборки. Параметр регуляризации 
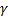подбирается либо из априорных соображений, либо по скользящему контролю (cross-validation).Оптимизация функционала генетическим алгоритмом достаточно тривиальна. Для первых экспериментов с данными вполне подойдет библиотека evoj. В дальнейшем лучше использовать коэволюционный алгоритм, чтобы эффективнее выбираться из локальных минимумов.В качестве заключения скажу, что данный метод можно использовать совместно с какой-либо латентной моделью, передавая предсказанную оценку записи в качестве одного из параметров линейного классификатора.
