Про семь цилиндров
Прочитав статью про семь соприкасающихся цилиндров, я задумался: действительно ли эта задача такая сложная? Или ей просто раньше никто всерьёз не занимался?Положение бесконечного цилиндра известного радиуса в пространстве задаётся четырьмя независимыми величинами (имеет 4 степени свободы). Для семи цилиндров в общем положении потребуется 28 величин. Каждое условие «два цилиндра касаются» даёт одно ограничение, всего остаётся 7 степеней свободы. Шесть из них — перемещения пространства, последнее остаётся на саму конфигурацию. То есть, у нас должно получиться одно или несколько однопараметрических семейств конфигураций, если только не помешает топология (из-за которой решений может не оказаться вообще).Вместо цилиндров нам удобнее работать с прямыми. Если диаметры двух цилиндров одинаковы и равны, допустим, единице, то они касаются (внешним образом) тогда и только тогда, когда расстояние между их осями равно единице. Учтём этот факт, и пойдём искать семь красных перпендикулярных прямых...Наша первая задача — по возможности, уменьшить количество переменных, которые описывают систему. Начнём с того, что избавимся от перемещений пространства. Скажем, что первая прямая — это ось Oz. Допустим, у нас есть другая прямая B, расстояние от которой до Oz равно 1. Пусть точка на B, ближайшая к Oz, имеет координаты (x,y,z). Тогда, как нетрудно увидеть, выполняется условие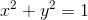 
, а направляющий вектор прямой B можно задать в виде (-y,x,d) для некоторого d. Таким образом, прямая задаётся 4 числами x, y, z, d с одним дополнительным условием.У нас всё ещё осталось две степени свободы перемещения пространства: сдвиг вдоль оси Oz и поворот вокруг неё. Зафиксируем их, выбрав для второй прямой x=1, y=z=0. Остальные 20 неизвестных (параметры оставшихся 5 прямых) дальше не ограничиваем.Условие на то, что расстояние между двумя прямыми с параметрами (x1, y1, z1, d1 и (x2, y2, z2, d2 равно 1, можно записать в виде
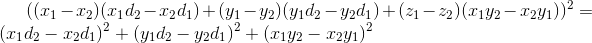Это уравнение 6-й степени, связывающее 8 неизвестных. Степень можно понизить до четвёртой, если взять несколько другую параметризацию прямой (сказать, что она проходит через точку (x,y,0) и имеет направляющий вектор (u,v,1)), но тогда мы потеряем прямые, перпендикулярные Oz.Итак, полиномиальное уравнение у нас есть. Осталось составить систему из 20 таких уравнений с 21 неизвестной, и подумать, что с ней делать. Запомним это, и поищем другой путь.Давайте скажем, что для некоторого угла
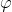. Тогда прямая у нас будет задаваться тремя параметрами 
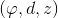, для второй прямой будем иметь 
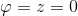, а уравнение, фиксирующее расстояние между двумя прямыми, будет выглядеть так:где
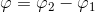. Это квадратное уравнение относительно z2-z1, то есть, зная величины мы легко можем получить два возможных значения z2-z1.План действий будет такой.
1. Попробуем воспользоваться случайным поиском. Сгенерируем случайный набор
. Для каждой прямой с 3-й по 7-ю запишем условие на расстояние до 2-й прямой — оно даст нам два возможных значения неизвестных z3,… z7. Для каждого из 32 возможных сочетаний этих значений проверим, насколько расстояния между оставшимися парами прямых будут отличаться от 1, и выберем наилучшее сочетание. Каким-нибудь оптимизационным методом попытаемся загнать все расстояния в 1. Если получилось — мы победили. Если нет — повторим ещё миллион раз.2. Если поиск не дал результатов — расширим перебор. Будем идти от всех возможных сочетаний z3,… z7.3. Заметим, что если у нас есть четыре соприкасающихся цилиндра, то число цилиндров, касающихся их всех, конечно. Построим каким-нибудь способом первые 4 цилиндра (у нас есть 4 степени свободы), потом поищем (случайным поиском) как можно больше соприкасающихся с ними цилиндров, выберем из них три штуки, попарные расстояния между осями которых как можно ближе к 1, и попытаемся соптимизировать полученный набор.4. То же самое, но во-первых, ищем все соприкасающиеся цилиндры, решая систему из 4 полиномиальных уравнений (в комплексном поле у неё 32 корня), а потом перебираем все тройки их осей.5. Если опять не повезло — начинаем думать, что же такое эти конфигурации и как их можно использовать.К сожалению, из этого плана ничего не вышло. Почему?Случайный поиск и оптимизация
Для оптимизации случайного решения я воспользовался самым испытанным методом — методом Ньютона. Правда, ему для работы нужно, чтобы число уравнений равнялось числу неизвестных, поэтому было принято решение зафиксировать неизвестную d2 (то есть, угол между первой и второй прямыми). Найти частные производные zk-zm по
— дело техники, и мы легко строим матрицу якобиана нашей системы размером 10*10. Правда, вместо обычной формулы x:=x-J-1f(x) я использовал более медленное движение x:=x-c*J-1f(x), где c изменялось от 0.1 до 0.001 (поскольку рельеф местности, по которой приходится блуждать, очень неровный и с большим количеством локальных минимумов). Далее оказалось, что этот метод обожает склеивать прямые, после чего пытается делить на 0 — пришлось объяснить ему, что если
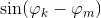для какой-нибудь пары прямых близок к нулю, то в данной попытке нас постигла неудача.Написать такой поиск было несложно. После исправления всех неучтённых моментов, запустил — и первое решение было найдено через несколько секунд, примерно на 9000-й попытке. За следующие 30 минут программа нашла 500 конфигураций, тогда в среднем удачной оказывалась одна из 7500 попыток.Независимая проверка показала, что решения правильные — расстояния между парами прямых отличались от 1 не больше, чем на 10-9. Но, просмотрев построенные картинки, я обнаружил, что многие из них чем-то похожи… Так что следующий вопрос был: какие из конфигураций одинаковы и в каком смысле?
Никаких идей, как подойти к этому вопросу, не было. Поэтому я вспомнил про оставшуюся степень свободы, и решил посмотреть, как цилиндры могут двигаться, не отрываясь друг от друга. Оказалось, что, например, вот так:Посчитав для каждой из конфигураций минимальную требуемую длину цилиндра (т.е. максимальное расстояние между точками касания на каждом цилиндре, измеренное вдоль оси), и построив графики, я пришел к выводу, что большая часть из найденных конфигураций даёт одну и ту же траекторию. Построить такую траекторию с мелким шагом и посчитать для каждой её конфигурации набор инвариантов, было несложно. Потом для каждого из найденных 500 решений я нашёл ближайшую к нему точку на этой траектории. 480 конфигураций попали прямо на траекторию, но 20 остальных были чем-то новым. Они вели себя вот так:Почему-то эта траектория хоть и заканчивается в бесконечности, но начинается в каком-то тупике, продолжить через который её не удаётся. Эту загадку я пока не разгадал. Кроме того, есть признаки, что две траектории в каком-то месте не то пересекаются, не то очень близко сходятся.В любом случае, 2-5 пункты плана не понадобились.
Перебрав ещё 70 миллионов точек и найдя более 10000 решений, программа не обнаружила ничего нового. Так что с пользой была истрачена только первая минута счёта...
