Применение FPGA для расчета деполимеризации микротрубочки методом броуновской динамики
Все готово, чтобы рассказать Хабр аудитории о применении FPGA в сфере научных высокопроизводительных вычислений. И о том, как на данной задаче надо удалось значительно обскакать GPU (Nvidia K40) не только в метрике производительность на ватт, но и просто с точки зрения скорости вычисления. В качестве FPGA платформы использовался кристалл Xilinx Virtex-7 2000t, подключенный по PCIe к хост компьютеру. Для создания аппаратного вычислительного ядра использовался язык C++ (Vivado HLS).
Под катом текст нашей оригинальной статьи. Там, как обычно бывает, сначала идет долгое описание зачем это все надо и модели, если нет желания это читать, то можно переходить сразу к реализации, а модель посмотреть потом при необходимости. С другой стороны без хотя бы беглого ознакомления с моделью читатель не сможет получить впечатление о том, какие сложные вычисления можно реализовать на FPGA)
Аннотация
В данной работе рассмотрена аппаратная реализация расчета деполимеризации белковой микротрубочки методом броуновской динамики на кристалле программируемой логической интегральной схемы (FPGA) Xilinx Virtex-7 с использованием высокоуровневого транслятора с языка Си Vivado HLS. Реализация на FPGA сравнивается с параллельными реализациями этого же алгоритма на многоядерном процессоре Intel Xeon и графическом процессоре Nvidia K40 по критериям производительности и энергоэффективности. Алгоритм работает на броуновских временах и поэтому требует большого количества нормально распределенных случайных чисел. Оригинальный последовательный код был оптимизирован под многоядердную архитектуру с помощью OpenMP, для графического процессора — с помощью OpenCL, а реализация на FPGA была получена посредством высокоуровневого транслятора Vivado HLS. В работе показано, что реализация на FPGA быстрее CPU в 17 раз и быстрее GPU в 11 раз. Что касается энергоэффективности (производительности на ватт), FPGA была лучше CPU в 160 раз и лучше GPU в 80 раз. Ускоренное на FPGA приложение было разработано с помощью SDK, включающего готовый проект FPGA, имеющий PCI Express интерфейс для связи с хост-компьютером, и софтверные библиотеки для общения хост-приложения с FPGA ускорителем. От конечного разработчика было необходимо только разработать вычислительное ядро алгоритма на языке Си в среде Vivado HLS, и не требовалось специальных навыков FPGA разработки.
Введение
Высокопроизводительные вычисления проводят на процессорах (CPU), объединенных в кластеры и/или имеющих аппаратные ускорители — графические процессоры на видеокартах (GPU) или программируемые логические интегральные схемы (FPGA) [1]. Современный процессор сам по себе является отличной платформой для высокопроизводительных вычислений. К достоинствам CPU можно отнести многоядерную архитектуру с общей когерентной кэш-памятью, поддержку векторных инструкций, высокую частоту, а также огромный набор рограммных средств, компиляторов и библиотек, обеспечивающий высокую гибкость программирования. Высокая производительность платформы GPU основывается на возможности запустить тысячи параллельных вычислительных потоков на независимых аппаратных ядрах. Для GPU доступны хорошо зарекомендовавшие себя средства разработки (CUDA, OpenCL), снижающие порог использования GPU платформы для прикладных вычислительных задач. Несмотря на это, в последние годы FPGA все чаще стали использоваться в качестве платформы для ускорения задач, в том числе использующих вещественные вычисления [2]. FPGA обладают уникальным свойством, резко отличающим их от CPU и GPU, а именно возможностью построить конвейерную аппаратную схему под конкретный вычислительный алгоритм. Поэтому, несмотря на значительно меньшую тактовую частоту, на которой работают FPGA (по сравнению с CPU и GPU), на некоторых алгоритмах на FPGA удается добиться большей производительности [3]–[5]. С другой стороны, меньшая частота работы означает меньшее энергопотребление, и FPGA практически всегда более эффективны, чем CPU и GPU, если использовать метрику «производительность на ватт» [5].
Одним из классических приложений, требующих высокопроизводительных вычислений является метод молекулярной динамики, использующийся для расчета движения систем атомов или молекул. В рамках этого метода взаимодействия между атомами и молекулами описываются в рамках законов Ньютоновской механики с помощью потенциалов взаимодействия. Расчет сил взаимодействия проводится итеративно и представляет существенную вычислительную сложность, учитывая большое количество атомов/молекул в системе и большое количество расчетных итераций. Ускорению расчетов молекулярной динамики было уделено много внимания в литературе в различных системах: суперкомпьютерах [6], кластерах [7], специализированных под молекулярно-динамические расчеты машинах [8]–[10], машинах c ускорителями на основе GPU [11] и FPGA [12]–[17]. Было продемонстрировано, что FPGA может являться конкурентной альтернативой в качестве аппаратного ускорителя для молекулярно-динамических вычислений во многих случаях, однако на сегодняшний день не существует консенсуса о том, для каких именно задач и алгоритмов выгоднее применять платформу FPGA. В данной работе мы рассматриваем важный частный случай молекулярной динамики — броуновскую динамику. Основная особенность метода броуновской динамики по сравнению с молекулярной динамикой заключается в том, что, молекулярная система моделируется более грубо, т.е. в качестве элементарных объектов моделирования выступают не отдельные атомы, а более крупные частицы, такие как отдельные домены макромолекул или целые макромолекулы. Молекулы растворителя и другие малые молекулы в явном виде не моделируются, а их эффекты учитываются в виде случайной силы. Таким образом удается значительно снизить размерность системы, что позволяет увеличить интервал времени, покрываемый модельными расчетами на порядки. Нам неизвестны описанные в литературе попытки исследовать эффективность FPGA по сравнению с альтернативными платформами для ускорения задач броуновской динамики. Поэтому мы предприняли исследование данного вопроса на примере задачи моделирования деполимеризации микротрубочки методом броуновской динамики. Микротрубочки — это трубки диаметром около 25 нм и длиной от нескольких десятков нанометров до десятков микрон, состоящие белка тубулина и входящие в состав внутреннего скелета живых клеток. Ключевой особенностью микротрубочек является их динамическая нестабильность, т.е. возможность спонтанно переключаться между фазами полимеризации и деполимеризации [18]. Это поведение важно прежде всего для захвата и перемещения хромосом микротрубочками во время клеточного деления. Кроме того, микротрубочки играют важную роль во внутриклеточном транспорте, движении ресничек и жгутиков и поддержании формы клетки [19].
Механизмы, лежащие в основе работы микротрубочек, исследуются уже несколько десятков лет, но лишь недавно развитие вычислительных технологий позволило описывать поведение микротрубочек на молекулярном уровне. Наиболее подробная молекулярная модель динамики микротрубочек, созданная недавно нашей группой на основе метода броуновской динамики, была реализована базе CPU и позволяла рассчитывать времена полимеризации/деполимеризации микротрубочек порядка нескольких секунд [20]. Это пролило свет на ряд важных аспектов динамики микротрубочек, однако, тем не менее, многие ключевые экспериментально наблюдаемые явления остались за рамками теоретического описания, т.к. они происходят в микротрубочках на временах десятков и даже сотен секунд [21]. Таким образом, для прямого сравнения теории и эксперимента критически важно достигнуть ускорения расчетов динамики микротрубочек хотя бы на порядок.
В данной работе мы исследуем возможность ускорения расчетов броуновской динамики микротрубочки на FPGA и сравниваем результаты, полученные при реализации одного и того же алгоритма динамики микротрубочек на трех разных платформах, по критериям производительности и энергоэффективности.
Математическая модель
Общие сведения о структуре микротрубочки
Структурно микротрубочка представляет собой цилиндр, состоящий из 13 цепочек — протофиламентов.

На рисунке слева — схема модели микротрубочки. Серым показаны субъединицы тубулина, черными точками — центры взаимодействия между ними. Справа — вид энергетических потенциалов взаимодействия между тубулинами.
Каждый протофиламент построен из димеров белка тубулина. Соседние протофиламенты связаны друг с другом боковыми связями и сдвинуты относительно друг друга на расстояние 3/13 длины одного мономера, так что микротрубочка имеет спиральность. При полимеризации димеры тубулина присоединяются к концам протофиламентов, причем протофиламенты микротрубочки стремятся принимать прямую конформацию. При деполимеризации боковые связи между протофиламентами на конце микротрубочки разрываются, и протофиламенты закручиваются наружу. При этом от них случайным образом отрываются олигомеры тубулина.
Моделирование деполимеризации микротрубочки методом броуновской динамики
Используемая здесь молекулярная модель микротрубочки была впервые представлена в статье [20]. Поскольку задачей настоящего исследования являлось сравнение производительности различных вычислительных платформ, мы ограничились моделированием только деполимеризации микротрубочки.
Вкратце, микротрубочка моделировалась как набор сферических частиц, представляющих собой мономеры тубулина. Мономеры могли двигаться только в соответствующей им радиальной плоскости, т.е. в плоскости, проходящей через ось микротрубочки и соответствующий протофиламент. Таким образом, положение и ориентация каждого мономера полностью определялись тремя координатами: двумя декартовыми координатами центра мономера и углом ориентации. Каждый мономер имел четыре центра взаимодействия на своей поверхности: два центра бокового взаимодействия и два центра продольного взаимодействия. Энергия тубулин-тубулинового взаимодействия зависела от расстояния r между сайтами взаимодействия на поверхности соседних субъединиц и от угла наклона между соседними мономерами тубулина в протофиламенте. Боковые и продольные взаимодействия между димерами тубулина определялись потенциалом, имеющим следующий вид:
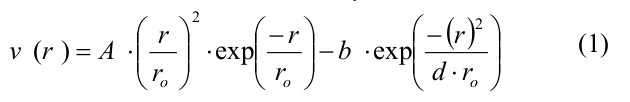
где A и b определяли глубину потенциальной ямы и высоту энергетического барьера, r0 и d — параметры, задающие ширину потенциальной ямы и форму потенциала в целом. Параметр A принимал различные значения для боковых и продольных связей, так что боковые взаимодействия были слабее продольных, все остальные параметры совпадали для обоих типов связей (полный список параметров и их значений представлен в Table 1 в [20]). Продольные взаимодействия внутри димера моделировались как неразрывные пружины с квадратичным энергетическим потенциалом u_r:
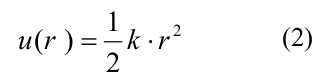
где k — жесткость связи тубулин-тубулинового взаимодействия. Энергия изгиба g (χ) связана с поворотом мономеров друг относительно друга и также описывалась квадратичной неразрывной функцией:

где χ — угол между соседними мономерами тубулина в протофиламенте, χ 0 — равновесный угол между двумя мономерами, B — изгибная жесткость. Полная энергия микротрубочки записывалась следующим образом:

где n — номер протофиламента, i — номер мономера в n-ом протофиламенте, Kn — число субъединиц тубулина в n-ом протофиламенте, бокового взаимодействия v_k_lateral — энергия бокового взаимодействия между мономерами, v_k_longitudinal — энергия продольного взаимодействия между димерами.
Эволюция системы рассчитывалось с помощью метода Броуновской динамики [22]. Изначальной конфигурацией микротрубочки была короткая «затравка», содержащая 12 мономеров тубулина в каждом протофиламенте. Мы рассматривали только деполимеризацию МТ и моделировали все тубулины с равновесным углом χ 0 = 0.2 рад. Координаты всех мономеров системы на i-ой итерации выражались следующим образом:
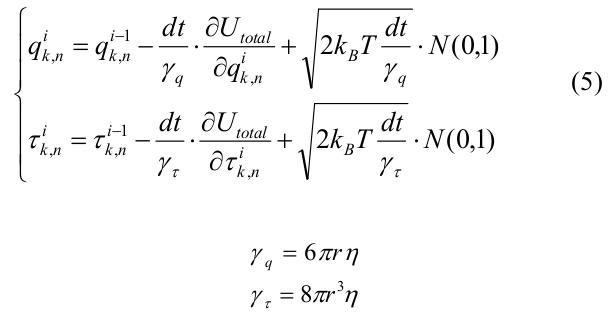
где dt — шаг по времени, U total выражается через (4), k_B — постоянная Больцмана, T- температура, N (0,1) — случайное число из нормального распределения, сгенерированное с помощью алгоритма вихрь Мерсенна [23]. γ q и γ τ — вязкостные коэффициенты сопротивления для сдвига и поворота соответственно, рассчитанные для сфер радиуса r = 2 нм.
Производная полной энергии по независимым координатам q{k, n} выражалась через боковую, продольную составляющие энергии взаимодействия между соседними димерами и внутри димера, а также энергию изгиба:
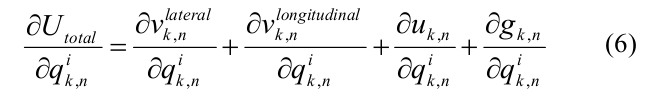
Для ускорения расчетов были использованы аналитические выражения для
всех градиентов энергии:
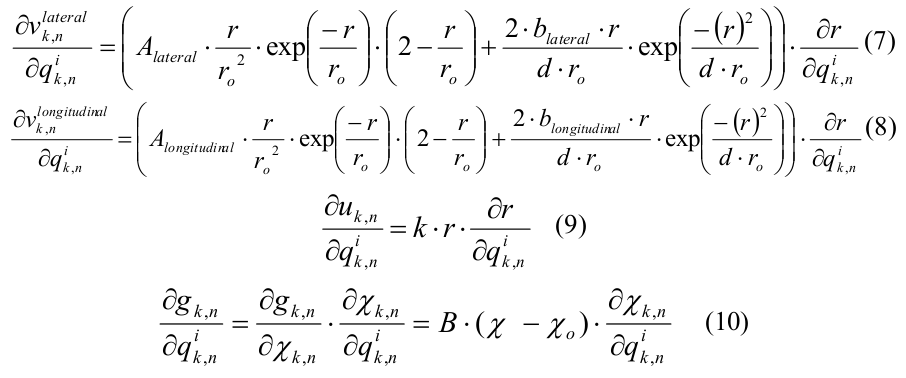
Следует отметить, что размер данной задачи сравнительно мал. Мы рассматривали только 12 слоев мономеров, что дает полное число частиц равное 156. Однако, это нисколько не уменьшает значимость вычислений, т.к. в реальных расчетах достаточно вычислять положение крайних нескольких (порядка 10) слов мономеров, т.к. при росте микротрубочки дальние от конца микротрубочки молекулы тубулина образуют устойчивую цилиндрическую конфигурацию, и брать их в расчет нет смысла.
Псевдокод алгоритма расчета
Алгоритм является итеративным по времени с шагом 0.2 нс. Существуют массив трехмерных координат молекул, а также массивы сил поперечного (латерального) и продольного (лонгитудального) взаимодействий. На каждой итерации по времени последовательно выполняются два вложенных цикла по молекулам, в первом производится вычисление сил взаимодействия по известным координатам, во втором — обновляются сами координаты. В цикле вычисления сил взаимодействия необходимо прочитать координаты трех молекул, одна центральная и две соседние («левая» и «верхняя», см. Рис. 2), а результатом вычисления будет сила поперечного взаимодействия между центральной и левой молекулами и сила продольного взаимодействия между центральной и верхней.
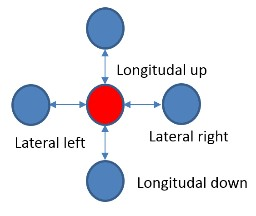
Рис. 2. Схема расположения взаимодействующих субъединиц в модели микротрубочки
В итоге после этого цикла оказываются вычисленными все силы взаимодействия между всеми молекулами. В цикле обновления координат по известным силам вычисляются изменения координат, а также берутся в расчет случайные добавки для учета Броуновского движения. Таким образом, псевдокод алгоритма можно записать следующим образом.
Вход: массив координат молекул M = {x, y, teta}. Граничные условия на силы
взаимодействия.
Выход: массив координат M после K шагов по времени
for t in {0.. K-1} do
for i in {0.. 13} // количество протофиламентов
for j in {0.. 12} do // количество слоев молекул
Mc <- M[i,j]
Ml <- M[i+1,j]
Mu <- M[i,j+1]
// по формулам (7, 8, 9, 10)
F_lat[i,j] <- calc_calteral(Mc, Ml)
F_long[i,j] <- calc_long(Mc, Mu)
end for
end for
for i in {0.. 13}
for j in {0.. 12} do
// по формулам (5)
M[i,j] <- update_coords(F_lat[i,j], F_long[i,j])
end for
end for
end forПрограммная реализация на CPU и GPU
Реализация на CPU
Была предпринята попытка максимально распараллелить код на CPU Intel Xeon E5–2660 2.20GHz под управлением ОС Ubuntu 12.04 с помощью библиотеки OpenMP. Параллельная секция начиналась до цикла по времени. Циклы расчета сил взаимодействия и обновления координат были распараллелены с помощью директивы omp for schedule (static), между циклами была вставлена барьерная синхронизация. Массивы, содержащие силы взаимодействия и координаты молекул, были объявлены как private для каждого потока.
При реализации расчетов на CPU было обнаружено, что размер задачи не позволял ее эффективно распараллелить. Зависимость времени выполнения одной итерации от числа параллельных потоков была немонотонна. Минимальное время расчета одной итерации по времени было получено при использовании всего 2 потоков (ядер CPU). Объясняется это тем что, с увеличением количества потоков растет время на копирование данных между потоками и на их синхронизацию. При этом размер задачи очень мал, чтобы выигрыш от увеличения количества ядер превысил эти накладные расходы. При этом эксперименты показали, что задача слабо масштабируется при увеличении размера (weak scaling), т.е. при дновременном увеличении размера задачи и числа параллельных потоков время вычисления оставалось примерно одинаковым. В итоге лучшим результатом на данном CPU было 22 мкс на одну итерацию по времени при использовании двух ядер CPU. Код не был векторизован из-за сложности вычислений сил взаимодействия.
Реализация на GPU
Мы запускали OpenCL реализацию на граф процессоре Nvidia Tesla K40. Циклы, вычисляющие силы взаимодействия и обновления координат были распараллелены, главный цикл по времени был итеративным. Были реализованы два варианта — с одной и несколькими рабочим группами (work groups). В первом случае было выделено по одному рабочему потоку (work item) на каждую молекулу. В каждом потоке был цикл по времени, в котором вычислялись силы и координаты молекулы потока. При этом применялась барьерная синхронизация после вычисления сил и после обновления координат. В этом случае участие хоста не требовалось для вычислений, он только занимался управлением и запуском ядер.
Во втором случае были два типа потоков, в одном просто вычислялись силы для одной молекулы, во втором — обновлялись координаты. Главный цикл по времени был на хосте, который управлял запуском и синхронизацией ядер на каждой итерации цикла по времени.
Наибольшая производительность была получена в расчетах с одной группой потоков и барьерной синхронизацией между ними. Без использования генераторов псевдослучайных чисел одна итерация вычислялась в течение 5 мкс, если использовать один генератор чисел на все потоки, то время работы возрастало до 9 мкс, а при максимальном заполнении общей памяти (shared memory) удавалось включить 7 независимых генераторов, при этом время вычисления одной итерации по времени составило 14 мкс, что было в 1.57 раза быстрее реализации на CPU.
Загруженность ядер GPU cоставила 7% от одного мультипроцессора (SM), при этом общая память, где размещались массивы сил, координат и буферы данных генераторов псевдослучайных чисел, была заполнена на 100%. Т.е. с одной стороны размер задачи был явно мал для полной загрузки GPU, с другой стороны при увеличении размера задачи пришлось бы использовать глобальную DDR память, что могло бы привести к ограничению роста производительности.
Реализация на FPGA
Описание платформы
Вычисления на FPGA производились на платформе RB-8V7 производства фирмы НПО «Роста». Она представляет собой 1U блок для установки в стойку. Блок состоит из 8 кристаллов FPGA Xilinx Virtex-7 2000T. Каждая FPGA имеет 1 GB внешней DDR3 памяти и PCI Express x4 2.0 интерфейс к внутреннему PCIe коммутатору. Блок имеет два интерфейса PCIe x4 3.0 к хост-компьютеру через оптические кабели, которые должны быть соединены со специальным адаптером, установленным в хост-компьютер.
В качестве хост-компьютера был использован сервер с CPU Intel Xeon E5–2660 2.20 GHz, работающий под управлением ОС Ubuntu 12.04 LTS — такой же как и для вычислений просто на CPU с помощью OpenMP. Программное обеспечение, работающее на CPU хост-компьютера «видит» блок RB-8V7 как 8 независимых FPGA устройств, подключенных по шине PCI Express. Далее будет описываться взаимодействие CPU только с одной FPGA XC7V72000T, при этом система позволяет использовать FPGA независимо и параллельно.
Ускоренное с помощью FPGA приложение было разработано с помощью SDK со следующей моделью. На CPU хост-компьютера (далее просто CPU) работает основная программа, которая использует ускоритель FPGA для наиболее вычислительно емких процедур. CPU передает данные в ускоритель и обратно через внешнюю DDR память, подключенную к FPGA, а также управляет работой вычислительного ядра в FPGA. Вычислительное ядро создается заранее на языке C/C++, верифицируется и транслируется в RTL код с помощью средства Vivado HLS. RTL код вычислительного ядра вставляется в основной FPGA проект, в котором уже реализована необходимая логика управления и передачи данных, включающая PCI Express ядро, DDR контроллер и шину на кристалле (Рис. 3). Основной FPGA проект иногда называют Board Support Package (BSP), он разрабатывается производителем оборудования, и от пользователя не требуется его модификации. Вычислительное ядро HLS после запуска само обращается в DDR память, считывает оттуда входной буфер данных для обработки и записывает туда же результат вычислений. На уровне языка C++ обращение в память происходит через аргумент функции верхнего уровня вычислительного ядра типа указатель.
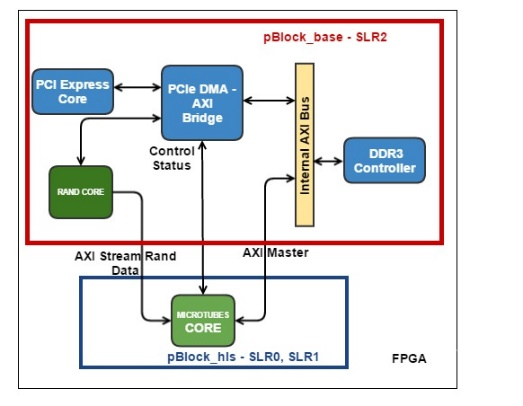
Рис. 3. Блок-схема проекта FPGA. Синим и желтым цветами отмечены блоки, входящие в BSP. Зеленым обозначены вычислительные HLS ядра. Также обозначено разбиение ядер проекта на блоки (pBlocks) для наложения пространсвенных ограничений при трассировке.
Для создания ускоренного приложения была разработана методология, состоящая из нескольких шагов. Во-первых, оригинальный последовательный код компилировался в среде Vivado HLS, и проверялось, что скомпилированный таких образом код не изменяет выходных данных опорного последовательного кода. Во-вторых, из этого кода выделялась основная вычислительная и подходящая для ускорения часть; эта часть отделялась от основного кода с помощью функции-обертки. После чего создавалось две копии такой функции и логика проверки на соответствие результатов обеих частей. Первая копия была опорной реализацией алгоритма в Vivado HLS, а вторая была оптимизирована для трансляции в RTL код. Оптимизации включали в себе переписывание кода, такие как использование статических массивов вместо динамических, использование специальных функций для ввода/вывода в HLS ядро, методы экономии памяти и переиспользования результатов вычислений. После каждого изменения результат функции сравнивался с результатом опорной реализации. Другим методом оптимизации было использование специальных директив Vivado HLS, не меняющих логическое поведение, но влияющих на конечную производительность RTL кода. На данной стадии следует оставаться до тех пор, пока не будут получены удовлетворительные предварительные результаты трансляции C в RTL, такие как производительность схемы и занимаемые ресурсы.
Следующая стадия — это имплементация разработанного вычислительного ядра в системе Vivado вне контекста основного проекта. Здесь задача добиться отсутствия временных ошибок уже разведенного дизайна внутри разработанного вычислительного ядра. Если на этом этапе наблюдаются временные ошибки, то можно применять другие параметры имплементации, либо возвращаться на предыдущую стадию и пытаться изменить С++ код или использовать другие директивы.
На следующей стадии необходимо имплементировать вычислительное ядро уже вместе с основным проектом и его временными и пространственными ограничениями. На данной стадии также необходимо добиться отсутствия временных ошибок. Если они наблюдаются, то можно либо изменить частоту работы вычислительной схемы, наложить другие пространственные ограничения на размещение схемы на кристалле, либо опять заняться
изменением C++ кода и/или использовать другие директивы.
Последняя стадия разработки — это проверка на соответствие результатов, полученных на реальном запуске в железе и с помощью опорной модели на CPU. Проходит она на небольшом промежутке времени, при этом считается, что на более длительных запусках (когда сравнить c CPU уже проблематично) FPGA решение выдает правильные результаты.
Работа в среде Vivado HLS
В работе использовалось два Vivado HLS ядра (Рис. 3): основное ядро, реализующее алгоритм молекулярной динамики микротрубочек (MT ядро), и ядро для генерации псевдослучайных чисел (RAND ядро). Нам пришлось разделить алгоритм на два вычислительных ядра по следующей причине. Кристалл FPGA Virtex-7 2000T — это самый большой кристалл FPGA семейства Virtex-7 на рынке. Он на самом деле состоит из четырех кристаллов кремния, соединенных на подложке множеством соединений и объединенных в один корпус микросхемы. По терминологии Xilinx каждый такой кристалл называется SLR (Super Logic Region). При использовании таких больших FPGA всегда возникают проблемы с цепями, пересекающими границы SLR. Xilinx рекомендует вставлять регистры на такие цепи с обеих сторон границы SLR.
Полное HLS ядро, включающее и MT и RAND ядра, требовали аппаратных ресурсов больше, чем было доступно в одном SLR, поэтому были цепи, которые пересекали границу независимых кристаллов кремния. На стадии трансляции с языка C++ в RTL Vivado HLS ничего «не знает» о том, какие цепи будут впоследствии пересекать границу, и поэтому не может заранее вставить дополнительные регистры синхронизации. Поэтому мы приняли решение разделить ядра на два, пространственно ограничить их в разные SLR и вставить регистры синхронизации на интерфейсные цепи между ядрами на уровне RTL.
Ядро MT
Данный алгоритм очень хорошо подходит для реализации на FPGA, потому для сравнительно небольшого количества данных из памяти (координаты двух молекул) необходимо вычислить сложную функцию сил взаимодействия и удается построить длинный вычислительный конвейер.
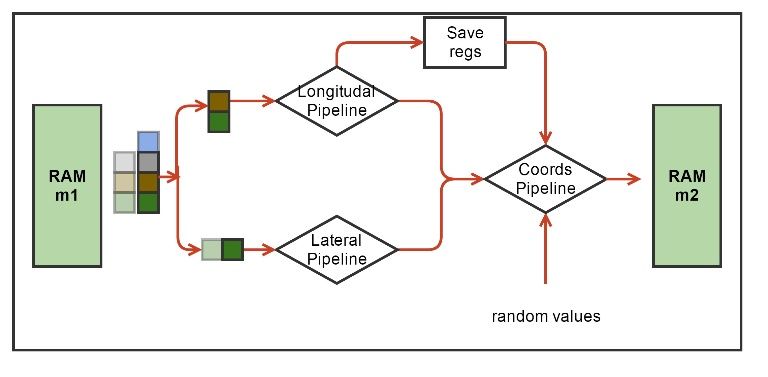
Рис. 4. Блок-схема аппаратной вычислительной процедуры ядра MT. Зеленым обозначены аппаратные блоки памяти для хранения координат молекул. Обозначены вычислительные конвейеры сил и обновления координат, а также блок Save Regs для хранения промежуточных результатов вычислений. Псевдослучайные числа поступают в конвейер обновления координат из другого HLS ядра.
Каждая молекула, т.е. мономер тубулина, взаимодействует только с четырьмя своими соседями (Рис. 2). На каждой итерации по времени надо сначала вычислить силы взаимодействия, а затем обновить координаты молекул. Функции вычисления сил взаимодействия включают в себя множество арифметических, экспоненциальных и тригонометрических операторов. Нашей первой задачей было синтезировать конвейер для этих функций. Рабочим типом данных был вещественный тип float. Vivado HLS синтезировала такие функции в виде конвейеров, работающих на частоте 200 МГц, с латентностью порядка 130 тактов. При этом конвейеры были однотактовые (или, как говорят, с интервалом инициализации равной 1), что означает, что на вход они могли принимать координаты новых молекул каждый такт, а затем после начальной задержки (латентности) — выдавать обновленные значения сил также каждый такт. Выходные силы взаимодействия использовались для обновления координат, что тоже было конвейеризовано. Для обновления каждой координаты каждой молекулы были необходимо независимые псевдослучайные нормально распределенные числа, получаемые из другого HLS ядра. Если взять три молекулы («текущую», «левую» и «верхнюю») то получилось возможным объединить конвейеры вычисления сил и обновления координат в один конвейер, реализующий все вычисления для одной молекулы. Такой конвейер имел латентность равную 191 такт (Рис. 4).
Алгоритм проходит по всем молекулам в цикле. На каждой итерации цикла необходимо иметь координаты трех молекул: одна молекула рассматривается как «текущая», также есть «левая» и «правая» молекулы. Соответственно рассчитываются силы взаимодействия между этими тремя молекулами. Далее при обновлении координат текущей молекулы левая и верхняя компоненты сил взаимодействия брались из расчета на текущей итерации, а нижняя и правая компоненты брались либо из граничных условий, либо с предыдущих итераций из локального регистрового файла Save Regs (Рис. 4).
Количество молекул N в системе было небольшим (13 протофиламентов х 12 молекул = 156 молекул). На каждую молекулу требуется 12 байт. Схема использовала два массива координат m1 и m2, общим объемом меньше 4 КБ, соответственно эти данные легко помещались во внутреннюю память FPGA — BRAM, реализованную внутри HLS ядра. Схема была устроена таким образом, что на четных итерациях по времени координаты считывались из массива m1 (и записывались в m2), а на нечетных — наоборот. С точки зрения алгоритма можно было читать и писать в один массив координат, но Vivado HLS не могла создать схему, способную на одном и том же такте читать и писать один и тот же аппаратный массив, что требуется для работы однотактового конвейера. Поэтому было принято решение удвоить количество независимых блоков памяти.
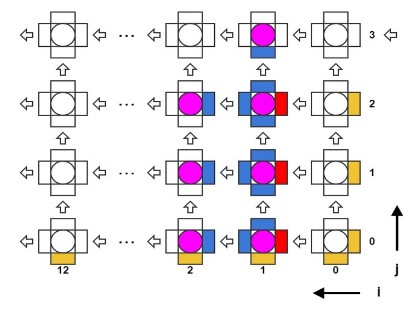
Рис. 5. Схема конвейерного расчета взаимодействий тубулинов в микротрубочке.
Оказалось возможным реализовать три полных параллельных конвейера, способных обновлять координаты трех молекул каждый такт (Рис. 5). Тогда во избежание простаивания конвейеров необходимо было увеличить пропускную способность к локальной памяти и читать координаты семи молекул каждый такт. Это проблема легко решилась, практически не меняя исходный C++ код, а лишь за счет использования специальной директивы,
физически разбивающей исходный массив данных по четырем независимым аппаратным
блокам памяти. Т.к. память BRAM в FPGA является двупортовой, то из четырех блоков памяти можно прочитать 8 значений за такт. Но, так как три конвейера требуют координаты 7 ми молекул за такт (см рис 5), это решило проблему.
#pragma HLS DATA_PACK variable=m1, m2
#pragma HLS ARRAY_PARTITION variable=m1, m2 cyclic factor=4 dim=2| Период | L | II | BRAM | DSP | FF | LUT | Утилизация |
|---|---|---|---|---|---|---|---|
| 5 нс | 191 такт | 1 такт | 52 | 498 | 282550 | 331027 | Абсолютная |
| 2% | 23% | 11% | 27% | Относительная |
Табл. 1: Производительность и утилизация схемы HLS с тремя полными конвейерами
В табл. 1 приводится утилизация схемы HLS (т.е. количество потребляемых ей аппаратных ресурсов FPGA, в абсолютных и относительных единицах для кристалла Virtex-7 2000T) и ее производительность. L — это задержка или латентность схемы, т.е. количество тактов между подачей в конвейер первых входных данных и получением первых выходных данных, II — это интервал инициализации (или пропускная способность) конвейера, означающее через сколько тактов на вход конвейера можно подавать следующие данные.
Утилизация приводится как в абсолютных величинах (сколько требуется триггеров FF или таблиц LUT) для реализации схемы, так и в относительных к полному количеству данного ресурса в кристалле. Как видно из табл. 1 латентность L полного конвейера была равна 191 такту, при этом каждый конвейер должен был обработать третью часть все молекул, что дает теоретическую оценку времени вычисления одной итерации равную T (FPGA) = (L+N/3)*5нс=1.2 мкс
Из табл. 1 также видно, что в кристалле осталось еще много неиспользованной логики, но дальше увеличивать количество параллельных конвейеров непрактично. Будет уменьшаться только второе слагаемое, а начальная задержка все равно будет давать значительный вклад во время работы. При этом увеличение количество логики усложнит размещение и трассировку схемы на следующих стадиях разработки проекта в Vivado.
Ядро RAND
Как было указано, алгоритм учитывает Броуновское движение молекул, одним из методов расчета которого является прибавление нормальной случайной добавки к изменению координат на каждой итерации по времени. Необходимо очень много нормально распределенных случайных чисел, на каждую итерацию — по N3 чисел, что дает поток 420 10 6 чисел/с. Такой поток не может быть загружен с хоста, поэтому его необходимо генерировать внутри FPGA «на лету». Для этого, как и в опорном коде для CPU, был выбран генератор вихрь Мерсенна, дающий равномерно распределенные псевдослучаные числа. Далее к ним применялось преобразование Бокса-Мюллера и на выходе получались нормально распределенные последовательности. Исходный открытый код вихря Мерсенна был модифицирован для получения аппаратного конвейера с интервалом инициализации в 1 такт. Алгоритм требует 9 нормальных чисел каждый такт, поэтому ядро RAND включало в себя 10 независимых генераторов вихря Мерсенна, т.к. преобразование Бокса-Мюллера требует два равномерно распределенных числа для получения 2х нормально распределенных. В табл. 2 приводится утилизация ядра RAND.
| BRAM | DSP | FF | LUT | Утилизация |
|---|---|---|---|---|
| 30 | 41 | 48395 | 64880 | Абсолютная |
| 1.2% | 9% | 0.1% | 5.3% | Относительная |
Табл. 2: Утилизация ядра RAND
Видно, что такое ядро требует значительную часть DSP ресурсов кристалла, и это ядро было бы сложно разместить в одном SLR с ядром MT, т.к. сумма утилизаций двух ядер хотя бы по DSP ресурсу 31% больше чем может вместить один SLR (25%).
Более подробно о том, как мы выбирали генератор псеводслучайных чисел и синтезировали его в Vivado HLS можно почитать в статье моей коллеги https://habrahabr.ru/post/266897/
Создание битстрима
После интеграции вычислительных ядер в Vivado на проект были наложены пространственные ограничения на размещение IP блоков. Используемая FPGA Virtex-7 2000T имеет 4 независимых кристалла кремния (SLR0, SLR1, SLR2, SLR3). Было показано, что ядро MT не умещалось в один SLR, поэтому было решено создать два региона размещение (pBlock): pBloch_hls для размещения только MT ядра и pBlock_base для размещения остальных ядер проекта (Рис. 3). Регион размещения pBlock_hls включал в себя SLR0 и SLR1, pBock_base — SLR2. Такой подход позволил разместить логику оптимальным образом, вставить регистры синхронизации на интерфейсы, пересекающие регионы размещения (а значит и SLR) и добиться положит
