Применяем мозаику Вороного, пикселизацию и геометрические маски в шейдерах для украшения сайта
Данная статья является логическим продолжением введения в программирование шейдеров для верстальщиков. В ней мы сделали шаблон для создания различных двумерных эффектов с фотографиями с помощью шейдеров и посмотрели пару примеров. В данной статье мы добавим еще пару текстур, применим на практике разбиение Вороного для создания мозаики из них, поговорим о создании различных масок в шейдерах, о пикселизации, а также затронем некоторые проблемы древнего синтаксиса GLSL, который до сих пор существует в наших браузерах.
Так же, как и в прошлый раз, будет минимум теории и максимум практики и рассуждений на приземленном бытовом языке. Начинающие найдут здесь последовательность действий с советами и полезными замечаниями, а опытные фронтендеры возможно найдут себе пару идей для вдохновения.
Опрос в предыдущей статье показал, что тема WebGL-эффектов для сайтов может быть интересна не только верстальщикам, но и нашим коллегам других специализаций. Чтобы не вводить их в недоумение последними фишками ES, мы намеренно ограничимся более традиционными синтаксическими конструкциями, понятными всем. И снова обращаю внимание читателей на то, что встроенные редакторы от CodePen влияют на производительность того, что в них выполняется.
Но приступим…
Шаблон для работы с шейдерами
Для тех, кто не читал предыдущую статью — мы сделали вот такой шаблон для работы с шейдерами:
В нем создается плоскость (в нашем случае квадрат), на которой «рисуется» картинка-текстура. Никаких лишних зависимостей и очень простой вершинный шейдер. Затем мы развивали этот шаблон, но сейчас начнем с момента, когда никакой логики во фрагментном шейдере еще нет.
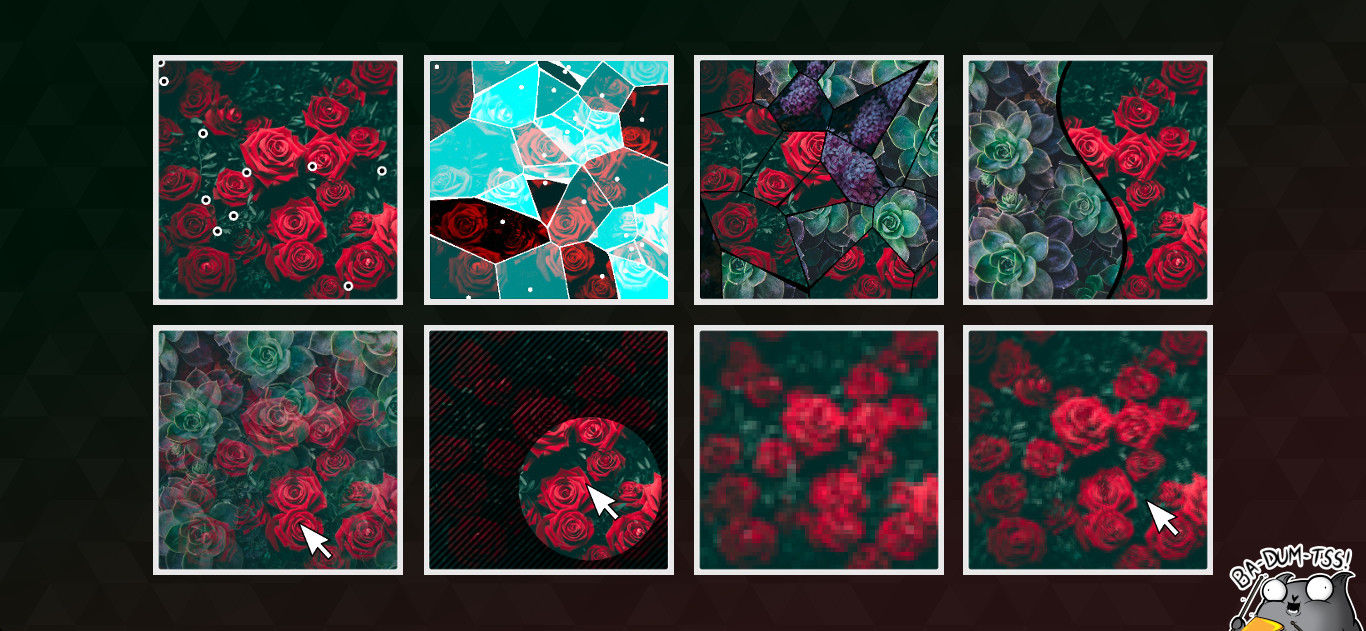
Мозаика
Мозаика — это разбитая на небольшие области плоскость, где каждая из областей заливается определенным цветом или, как в нашем случае, текстурой. Как мы вообще можем разбить нашу плоскость на кусочки? Очевидно, что можно разбить ее на прямоугольники. Но это и так легко сделать с помощью SVG, приплетать к этой задаче WebGL и все уложнять на ровном месте совершенно ни к чему.
Чтобы мозаика была интересной, в ней должны быть разные фрагменты, как по форме, так и по размеру. Есть один очень простой, но в то же время очень занятный подход к построению такого разбиения. Он известен как мозаика Вороного или разбиение Дирихле, а на википедии пишут, что еще Декарт использовал что-то подобное в далеком XVII веке. Идея примерно такая:
- Взять набор точек на плоскости.
- Для каждой точки на плоскости найти ближайшую к ней точку из этого набора.
- Собственно вот и все. Плоскость поделилась на многоугольные области, каждая из которых определяется одной из точек набора.
Наверное лучше показать этот процесс на практическом примере. Есть разные алгоритмы генерации этого разбиения, мы же будем действовать в лоб, ибо расчет чего-то для каждой точки на плоскости — это как раз задача для шейдера. Для начала нам нужно сделать набор случайных точек. Чтобы не загружать код примеров сделаем глобальную переменную для них.
function createPoints() {
for (let i = 0; i < NUMBER_OF_POINTS; i++) {
POINTS.push([Math.random(), Math.random()]);
}
}
Теперь нам нужно передать их в шейдеры. Данные глобальные, так что будем использовать модификатор uniform. Но здесь есть один тонкий момент: просто так передать массив мы не можем. Казалось бы, 21 век на дворе, но тем не менее ничего не выйдет. В результате приходится передавать массив точек по одной штуке.
for (let i = 0; i < NUMBER_OF_POINTS; i++) {
GL.uniform2fv(GL.getUniformLocation(PROGRAM, 'u_points[' + i + ']'), POINTS[i]);
}
Сегодня мы не раз столкнемся с подобными проблемами несоответствия ожидаемого и того, что есть в реальных браузерах. Обычно в уроках по WebGL используют THREE.js и эта библиотека скрывает часть грязи в себе, как когда-то это делала jQuery в своих задачах, но стоит ее убрать, как реальность больно бьет по мозгам.
Во фрагментном шейдере мы имеем переменную-массив для точек. Мы можем создавать массивы только фиксированной длины. Пусть для начала это будет 10 точек:
#define NUMBER_OF_POINTS 10
uniform vec2 u_points[NUMBER_OF_POINTS];
Убедимся в работоспособности всего этого нарисовав круги на местах точек. Подобное рисование различных геометрических примитивов часто применяется при отладке — их хорошо видно и сразу можно понять, что где находится и куда движется.
Используйте «рисование» кругов, прямых и других ориентиров для невидимых объектов, на которых строятся анимации. Это даст очевидные подсказки о том, как они работают, особенно если алгоритмы сложны для быстрого понимания без предварительной подготовки. Потом это все можно закомментировать и оставить для коллег — они скажут спасибо.
for (int i = 0; i < NUMBER_OF_POINTS; i++) {
if (distance(texture_coord, u_points[i]) < 0.02) {
gl_FragColor = WHITE;
break;
}
}
Хорошо. Давайте также добавим немного движения точкам. Пусть они двигаются по кругу для начала, мы потом еще вернемся к этому вопросу. Коэффициенты поставлены также на глазок, просто чтобы немного замедлить их движение и уменьшить амплитуду колебаний.
function movePoints(timeStamp) {
if (timeStamp) {
for (let i = 0; i < NUMBER_OF_POINTS; i++) {
POINTS[i][0] += Math.sin(i * timeStamp / 5000.0) / 500.0;
POINTS[i][1] += Math.cos(i * timeStamp / 5000.0) / 500.0;
}
}
}
Возвращаемся в шейдер. Для будущих экспериментов нам пригодятся номера областей, на которые все поделится. Так что мы находим ближайшую к текущему пикселю точку из набора и сохраняем номер этой точки — он же номер области.
float min_distance = 1.0;
int area_index = 0;
for (int i = 0; i < NUMBER_OF_POINTS; i++) {
float current_distance = distance(texture_coord, u_points[i]);
if (current_distance < min_distance) {
min_distance = current_distance;
area_index = i;
}
}
Для проверки работоспособности опять же покрасим все в яркие цвета:
gl_FragColor = texture2D(u_texture, texture_coord);
gl_FragColor.g = abs(sin(float(area_index)));
gl_FragColor.b = abs(sin(float(area_index)));
Сочетание модуля (abs) и ограниченных функций (в частности sin и cos) часто применяют при работе с подобными эффектами. Это с одной стороны добавляет немного случайности, а с другой стороны сразу дает нормализованный результат от 0 до 1, что очень удобно — у нас очень многие значения будут лежать именно в этих пределах.
Также найдем точки, более-менее равноудаленные от нескольких точек из набора, и покрасим их. Это действие не несет особой полезной нагрузки, но посмотреть на результат все равно интересно.
int number_of_near_points = 0;
for (int i = 0; i < NUMBER_OF_POINTS; i++) {
if (distance(texture_coord, u_points[i]) < min_distance + EPSILON) {
number_of_near_points++;
}
}
if (number_of_near_points > 1) {
gl_FragColor.rgb = vec3(1.0);
}
Должно получиться что-то такое:
Это пока черновой вариант, мы его еще будем дорабатывать. Но уже сейчас понятна общая концепция подобного разделения плоскости.
Мозаика из фотографий
Понятное дело, что в чистом виде пользы от такого разбиения не очень много. Для расширения кругозора и просто ради интереса можно с ним поиграть, но на реальном сайте стоило бы добавить еще пару фотографий и сделать мозаику из них. Давайте немного переделаем функцию создания текстур, чтобы их было больше одной.
function createTextures() {
for (let i = 0; i < URLS.textures.length; i++) {
createTexture(i);
}
}
function createTexture(index) {
const image = new Image();
image.crossOrigin = 'anonymous';
image.onload = () => {
const texture = GL.createTexture();
GL.activeTexture(GL['TEXTURE' + index]);
GL.bindTexture(GL.TEXTURE_2D, texture);
GL.pixelStorei(GL.UNPACK_FLIP_Y_WEBGL, true);
GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGB, GL.RGB, GL.UNSIGNED_BYTE, image);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.LINEAR);
GL.uniform1i(GL.getUniformLocation(PROGRAM, 'u_textures[' + index + ']'), index);
};
image.src = URLS.textures[index];
}
Ничего необычного не произошло, мы только заменили нули на параметр index и переиспользовали уже имеющийся код, чтобы загрузить три текстуры. В шейдере у нас теперь массив из текстур:
#define NUMBER_OF_TEXTURES 3
uniform sampler2D u_textures[NUMBER_OF_TEXTURES];
Теперь мы можем использовать номер области, сохраненный ранее, для того, чтобы выбрать одну из трех текстур. Но…
Но перед этим хотелось бы сделать небольшое отступление. О наболевшем. О синтаксисе. Современный Javascript (условно ES6+) — это приятный язык. Он позволяет выражать свои мысли по мере их возникновения, не ограничивает рамками какой-то конкретной парадигмы программирования, некоторые моменты доделывает за нас и позволяет больше сосредоточиться на идее, чем на ее реализации. Для творца — самое то. Некоторые люди считают, что он дает слишком много свободы и переходят на TypeScript к примеру. Чистый Си — это более строгий язык. Он тоже многое позволяет, на нем можно нашаманить все, что угодно, но после JS он воспринимается немного неуклюжим, старомодным что ли. Но тем не менее он все еще хорош. GLSL в том виде, в котором он существует в браузерах — это просто нечто. Мало того, что он на порядок строже, чем Си, так в нем еще отсутствуют многие привычные операторы и синтаксические конструкции. Это наверное самая большая проблема при написании более-менее сложных шейдеров для WebGL. За тем ужасом, в который превращается код, бывает очень непросто раглядеть изначальный алгоритм. Некоторые верстальщики думают, что пока они не выучили Си, путь к шейдерам для них закрыт. Так вот: знание Си тут особо не поможет. Здесь какой-то свой мир. Мир безумия, динозавров и костылей.
Как можно выбрать одну из трех текстур имея одно число — номер области. На ум приходит остаток от деления номера на количество текстур. Отличная идея. Только оператора %, который руки сами уже пишут, здесь нет. Впечатление от понимания этого факта хорошо описывает картинка:

Вы конечно скажете «да не проблема, есть же функция mod — возьмем ее!». Но оказывается, что она не принимает два целых числа, только дробные. Ок, хорошо, делаем из них float. Получаем тоже float, но нам нужен int. Приходится преобразовывать все обратно, иначе есть неиллюзорный шанс получить ошибку при компиляции.
int texture_index = int(mod(float(area_index), float(NUMBER_OF_TEXTURES)));
И вот риторический вопрос:, а может быть проще будет реализовать свою функцию остатка от деления целых чисел, чем пытаться собрать ее из стандартных методов? И это еще простая функция, а бывает, что получаются очень глубоко вложенные последовательности таких преобразований, в которых уже не совсем понятно, что происходит.
Ладно, оставим пока все как есть. Просто возьмем цвет нужного пикселя из выбранной текстуры и присвоим его переменной gl_FragColor. Так? Мы ведь уже делали это? И тут этот кот появляется еще раз. Нельзя использовать не-константу при обращении к массиву. А все, что мы рассчитали — это уже не константа. Ba-dum-tsss!!!
Приходится делать что-то такое:
if (texture_index == 0) {
gl_FragColor = texture2D(u_textures[0], texture_coord);
} else if (texture_index == 1) {
gl_FragColor = texture2D(u_textures[1], texture_coord);
} else if (texture_index == 2) {
gl_FragColor = texture2D(u_textures[2], texture_coord);
}
Согласитесь, такому коду прямая дорога на govnokod.ru, но тем не менее по-другому никак. Даже оператора switch-case здесь нет, чтобы хоть как-то облагородить это безобразие. Есть правда еще другой, менее очевидный костыль, решающий эту же задачу:
for (int i = 0; i < 3; i++) {
if (texture_index == i) {
gl_FragColor = texture2D(u_textures[i], texture_coord);
}
}
Счетчики циклов, которые увеличиваются на единицу, компилятор может считать за константу. Но с массивом текстур такое провернуть не получилось — в последнем Хроме вылезла ошибка, говорящая, что именно с массивом текстур так делать нельзя. С массивом чисел получалось. Угадайте, почему с одним массивом работает, а с другим — нет? Если вы думали, что система приведения типов в JS полна магии — разберитесь в системе «константа — не константа» в GLSL. Самое забавное тут то, что результаты зависят и от используемой видеокарты, так что хитрые костыли, которые сработали на видеокарте от NVIDIA вполне могут внезапно сломаться на AMD.
Лучше избегать подобных решений, основанных на предположениях о работе компилятора. Они имеют свойство ломаться и плохо поддаются тестированию.
Грусть-печаль. Но, если мы хотим делать интересные вещи, нужно абстрагироваться от всего этого и продолжить.
На данный момент мы получили мозаику из фотографий. Но есть одна деталь: если точки подходят друг к другу очень близко, то происходит быстрый переход двух областей. Это не очень красиво. Нужно добавить какой-нибудь алгоритм, не позволяющий точкам сближаться. Можно сделать простой вариант, при котором проверяются расстояния между точками и, если оно меньше некоторого значения, то мы их раздвигаем. Этот вариант не лишен недостатков, в частности он иногда приводит к небольшому дерганию точек, но во многих случаях его может быть достаточно, тем более, что расчетов здесь получается не очень много. Более продвинутыми вариантами были бы система движущихся зарядов и «паутинка», в которой пары точек соединены невидимыми пружинками. Если вам будет интересно их реализовать, то все формулы вы без труда найдете в справочнике по физике для средней школы.
for (let i = 0; i < NUMBER_OF_POINTS; i++) {
for (let j = i; j < NUMBER_OF_POINTS; j++) {
let deltaX = POINTS[i][0] - POINTS[j][0];
let deltaY = POINTS[i][1] - POINTS[j][1];
let distance = Math.sqrt(deltaX * deltaX + deltaY * deltaY);
if (distance < 0.1) {
POINTS[i][0] += 0.001 * Math.sign(deltaX);
POINTS[i][1] += 0.001 * Math.sign(deltaY);
POINTS[j][0] -= 0.001 * Math.sign(deltaX);
POINTS[j][1] -= 0.001 * Math.sign(deltaY);
}
}
}
Главная проблема этого подхода, а также того, который мы использовали в шейдере — сравнение всех точек со всеми. Не нужно быть великим математиком, чтобы понять, что количество расчетов дистанций будет просто невероятным, если мы сделаем не 10 точек, а 1000. Да даже 100 хватит, чтобы все тормозило. Поэтому его имеет смысл применять только для небольшого количества точек.
Если мы хотим сделать такую мозаику для большого количества точек, то можно воспользоваться уже знакомым нам делением плоскости на одинаковые квадраты. Идея в том, чтобы в каждый квадрат поместить одну точку, а потом все сравнения проводить только с точками из соседних квадратов. Мысль хорошая, но эксперименты показали, что при большом количестве точек недорогие ноутбуки со встроенными видеокартами все равно не справляются. Поэтому стоит десять раз подумать, прежде чем решать сделать у себя на сайте такую мозаику из большого количества фрагментов.
Не будьте редисками, проверяйте быстродействие своих поделок не только на своей майнинг ферме, но и на обычных ноутбуках. У пользователей в основном будут именно они.
Разбиение плоскости на части по графику функции
Давайте посмотрим еще один вариант разделения плоскости на части. Он уже не потребует больших вычислительных мощностей. Основная идея в том, чтобы взять какую-нибудь математическую функцию и построить ее график. Полученная линия как раз поделит плоскость на две части. Если мы будем использовать функцию вида y = f(x), то получим деление в виде разреза. Заменяя X на Y мы сможем менять горизонтальный разрез на вертикальный. Если взять функцию в полярных координатах, то потребуется переводить все в декартовы и обратно, но суть вычислений не изменится. В таком случае получится не разрез на две части, а скорее вырезание дырки. Но мы посмотрим первый вариант.
Для каждого Y мы будем рассчитывать значение X, чтобы сделать вертикальный разрез. Мы могли бы взять для этих целей синусоиду например, но это слишком скучно. Лучше взять их сразу несколько штук и сложить.
Берем несколько синусоид, каждая из которых привязана к координате по Y и ко времени, и складываем их. Физики назвали бы такое сложение суперпозицией. Очевидно, что умножая весь результат на какое-то число, мы меняем амплитуду. Выносим это в отдельный макрос. Если умножать координату — параметр синуса, то будет меняться частота. Мы уже видели это в прошлой статье. Также выносим из формулы общий для всех синусоид модификатор частоты. Будет не лишним поиграть и со временем, отрицательный знак даст эффект движения линии в обратную сторону.
float time = u_time * SPEED;
float x = (sin(texture_coord.y * FREQUENCY)
+ sin(texture_coord.y * FREQUENCY * 2.1 + time)
+ sin(texture_coord.y * FREQUENCY * 1.72 + time * 1.121)
+ sin(texture_coord.y * FREQUENCY * 2.221 + time * 0.437)
+ sin(texture_coord.y * FREQUENCY * 3.1122 + time * 4.269))
* AMPLITUDE;
Сделав такие глобальные настройки для нашей функции мы столкнемся с проблемой повторения одного и того же движения через довольно небольшие промежутки времени. Для того, чтобы решить этот вопрос, нам нужно все умножить на коэффициенты, у которых наименьшее общее кратное очень большое. Что-то похожее используется и в генераторе случайных чисел, помните? В данном случае мы не стали думать и взяли готовые числа из какого-то примера из интернета, но никто не мешает поэкспериментировать со своими значениями.
Остается только выбрать одну из двух текстур для точек выше нашего графика функции и вторую для точек ниже него. Точнее сказать левее и правее, мы ведь все повернули:
if (texture_coord.x - 0.5 > x) {
gl_FragColor = texture2D(u_textures[0], texture_coord);
} else {
gl_FragColor = texture2D(u_textures[1], texture_coord);
}
То, что мы получили, напоминает звуковые волны. Точнее их изображение на осциллографе. И действительно, мы могли бы вместо своих синусоид передавать данные из какого-нибудь звукового файла. Но работа со звуком — это тема для отдельной статьи.
Маски
Предыдущие примеры должны натолкнуть на вполне логичное замечание: все это похоже на работу масок в SVG (если вы с ними не работали — посмотрите примеры из статьи SVG-маски и вау-эффекты). Просто здесь мы их делаем немного по-другому. А в результате получается то же самое — какие-то области закрашиваются одной текстурой, какие-то другой. Только плавных переходов еще не было. Так что давайте сделаем один.
Убираем все лишнее и возвращаем координаты мыши. Сделаем радиальный градиент с центром в месте расположения курсора и будем использовать его в качестве маски. В этом примере поведение шейдера будет больше напоминать логику работы масок в SVG, чем в предыдущих примерах. Нам понадобится функция mix и какая-нибудь функция от расстояния. Первая будет смешивать значения цветов пикселей из обеих текстур, принимая в качестве третьего параметра коэффициент (от 0 до 1), определяющий то, какое из значений будет преобладать в результате. В качестве функции от расстояния возьмем модуль синуса — она как раз будет давать плавное изменение значения между 0 и 1.
gl_FragColor = mix(
texture2D(u_textures[0], texture_coord),
texture2D(u_textures[1], texture_coord),
abs(sin(length(texture_coord - u_mouse_position / u_canvas_size))));
Собственно вот и все. Посмотим на результат:
Главное преимущество по сравнению с SVG очевидно:
В отличии от SVG, здесь мы можем легко делать плавные градиенты по различным математическим функциям, а не собирать их из множества линейных градиентов.
Если у вас более простая задача, не требующая таких плавных переходов или сложных форм, которые рассчитываются в процессе, то скорее всего ее будет проще реализовать без использования шейдеров. Да и производительность на слабом железе скорее всего будет лучше. Выбирайте инструмент исходя из своих задач.
В образовательных целях посмотрим еще один пример. Для начала делаем круг, в котором текстура будет оставаться такой, какая она есть:
gl_FragColor = texture2D(u_textures[0], texture_coord);
float dist = distance(texture_coord, u_mouse_position / u_canvas_size);
if (dist < 0.3) {
return;
}
А все остальное заполняем диагональными полосками:
float value = sin((texture_coord.y - texture_coord.x) * 200.0);
if (value > 0.0) {
gl_FragColor.rgb *= dist;
} else {
gl_FragColor.rgb *= dist / 10.0;
}
Примемы все те же — умножаем параметр для синуса, чтобы увеличить частоту полосок; делим полученные значения на две части; для каждой из половин преобразуем цвет пикселей по-своему. Полезно помнить, что рисование диагональных линий обычно связано со сложением координат по X и по Y. Обратите внимание, что мы все также используем расстояние до курсора мыши при изменении цветов, тем самым создавая своеобразную тень. Таким же образом можно использовать его и при геометрических трансформациях, мы скоро посмотрим это на примере пикселизации. А пока взглянем на результат работы этого шейдера:
Просто и симпатично.
И да, если немного заморочиться, то можно делать текстуры не из картинок, а из кадров из видео (в сети много примеров, вы без труда с ними разберетесь), и применять все наши эффекты к ним. На многих сайтах из каталогов вроде Awwwards используют подобные эффекты именно в сочетании с видео.
Стоит помнить и еще одну мысль:
Никто не мешает использовать одну из текстур в качестве маски. Мы можем брать картинку и использовать значения цветов ее пикселей в наших преобразованиях, будь то изменения других цветов, сдвиги в стороны или еще что-то, что придет вам в голову.
Но вернемся к разбиению плоскости на части.
Пикселизация
Этот эффект в некоторой степени очевиден, но в то же время он так часто встречается, что пройти мимо было бы неправильно. Делим нашу плоскость на квадраты, таким же образом, как это было в примере с генератором шума, а затем для всех пикселей внутри каждого квадрата задаем один и тот же цвет. Он получается в результате смешивания значений из углов квадрата, мы уже делали что-то подобное. Для данного эффекта нам не нужны сложные формулы, так что просто складываем все значения и делим на 4 — количество углов у квадрата.
float block_size = abs(sin(u_time)) / 20.0;
vec2 block_position = floor(texture_coord / block_size) * block_size;
gl_FragColor = (
texture2D(u_textures[0], block_position)
+ texture2D(u_textures[0], block_position + vec2(1.0, 0.0) * block_size)
+ texture2D(u_textures[0], block_position + vec2(0.0, 1.0) * block_size)
+ texture2D(u_textures[0], block_position + vec2(1.0, 1.0) * block_size)
) / 4.0;
Мы снова привязали один из параметров ко времени через модуль синуса, чтобы наглядно посмотреть, что происходит при его изменении.
Пиксельные волны
Напоследок мы еще раз применим уже известные нам приемы в одном месте, чтобы добавить волны в пример с пикселями.
float block_size = abs(sin(
length(texture_coord - u_mouse_position / u_canvas_size)
* 2.0 - u_time)) / 100.0 + 0.001;
Используем модуль синуса, чтобы загнать все в пределы от 0 до 1; добавляем расстояние от текущего положения до курсора мыши, время, и подбираем немного коэффициентов, чтобы все это выглядело красиво. К результату добавляем небольшую константу для того, чтобы не было нулевых размеров блоков.
Это довольно своеобразные «пиксельные» волны, но точно также можно было бы взять сдвиги из предыдущей статьи и рассчитывать их, а не размеры блоков-пикселей. Тогда получатся более натуральные волны. Также никто не мешает сделать несколько «точек волнения», волны из которых будут смешиваться, как мы смешивали синусы в одном из предыдущих примеров. Простор для фантазии достаточно широкий. Единственное о чем следует помнить — это производительность. Не стоит злоупотреблять с большим количеством вычислений.
Итоги
Взяв за основу шаблон из введения в программирование шейдеров, мы реализовали несколько популярных эффектов, посмотрели идеи, которые в них заложены, повторили пару раз и добавили их к себе в копилку знаний. Дальнейшее изучение шейдеров в контексте двумерных эффектов будет сводиться ко всевозможным экспериментам и реализации своих фантазий или идей наших коллег-дизайнеров. Подобные вещи уже сложно как-то систематизировать и представить в виде последовательности более-менее связанных примеров. Поэтому на этом моменте мы остановимся с разбором двумерных эффектов. Начинающим разработчикам хотелось бы пожелать терпения в изучении этой темы. Это одна из областей, в которых нет проверенных путей развития, так что вам придется много экспериментировать, чтобы начать свободно делать подобные вещи.
P.S.: Какие темы, связанные с WebGL (или с разработкой нестандартных сайтов в целом) на ваш взгляд стоило бы затронуть в статьях на Хабре? Область эта достаточно широкая и, насколько я понимаю, не очень систематизированная. На какие темы стоило бы обратить внимание в первую очередь?
