Представление движений в 3D моделировании: интерполяция, аппроксимация и алгебры Ли
Сколько существует разных способов представить обыкновенный поворот в трехмерном пространстве? Большинство людей, когда-либо занимавшихся 3D-графикой или 3D-моделированием, сходу назовут три основных широко распространенных варианта:
- Матрица поворота 3×3;
- Задание поворота через углы Эйлера;
- Кватернионы.
Люди с богатым опытом добавят сюда почему-то не пользующийся популярностью четвертый пункт:
- Ось поворота и угол.
Мне бы хотелось рассказать о пятом способе представления вращений, который симпатичен тем, что удобен для параметризации, позволяет эффективно строить полиномиальные аппроксимации этих параметризаций, проводить сферическую интерполяцию, и главное, универсален — с минимальными изменениями он работает для любых видов движений. Если вам когда-либо был нужен метод, который позволял бы легко сделать «аналог slerp, но не для чистых вращений, а для произвольных движений, да еще и с масштабированием», то читайте эту статью.
Я начну с математического описания того, откуда возникает пятый способ представления вращений, чем именно является возникающая параметризация, но все желающие могут пропустить этот раздел и сразу перейти к практической части в конце статьи.
Группы и алгебры Ли: на стыке алгебры и дифференциальной геометрии
Вращения объекта в трехмерном пространстве (и, обобщая, любые движения объекта) с математической точки зрения являются типичным примером структуры которая называется «группой». Групповой операцией здесь является «комбинирование», когда вначале применяется одно движение, а затем второе; эта комбинация, очевидно, тоже является движением. Единицей группы служит тривиальное движение «ничего не менять». Для любого движения можно отыскать обратное движение, позволяющее «вернуть все как было». С практической стороны, применительно к геометрии, существование группы часто говорит о существовании какой-то «особенности» данного движения, которая сохраняется в пределах группы. Например, если мы передвинули куда-то объект чистым вращением, то вернуть его обратно можно тоже чистым вращением. Группа движений евклидового пространства сохраняет расстояния между точками передвигаемого объекта. Группа симметрий куба состоит из 48 движений, которые переводят куб в самого себя. Это то, что более-менее известно всем.
Легко однако заметить, что группа вращений устроена в определенном смысле «интереснее» чем группа симметрий куба. Так, мы знаем, что для вращений можно интерполировать непрерывное движение между любыми двумя точками (найти функцию, которая плавно и непрерывно повернет объект из одного положения в другое), тогда как для 48 элементов группы симметрий куба это, очевидно, невозможно. Еще одним интересным свойством является возможность локально параметризовывать элементы этой группы тройками чисел (к примеру, углами Эйлера). В математических терминах все эти свойства формализуют фразой «группа вращений является гладким многообразием». То есть мы можем представить себе пространство всех возможных поворотов в трехмерном пространстве как некоторую многомерную поверхность типа сферы. Только вот обычная сфера является двумерной поверхностью и ее можно поместить (вложить) в трехмерное пространство, а пространство вращений является трехмерной гиперповерхностью и для того чтобы ее изобразить потребуется четырехмерное пространство;, а чтобы сделать это без самопересечений — шестимерное, причем получившаяся в этом пространстве поверхность для группы вращений топологически будет напоминать скорее бублик, чем сферу. Но математика там получается практически такой же, поэтому я буду использовать обычную двумерную сферу для интуитивной иллюстрации понятия «гладкого многообразия».
Рассмотрим теперь непрерывное движение какого-то объекта, заданное функцией положения объекта в зависимости от момента времени f (t). Скажем, f (0) может определять начально положение объекта, f (1) — конечное, а f (0.5) тогда будет соответствовать положению объекта на «середине дороги» от начальной точки к конечной. Поскольку отдельные положения объекта являются точками на нашем гладком многообразии, то считая f (t) в разных точках, можно построить на нашей «сфере» цепочку из точек, связывающую между собой начальную и конечную точки на «сфере»; в пределе, как несложно понять, эта цепочка объединяется в непрерывную кривую. То есть разные кривые на нашем многообразии являются разными траекториями движения объектов и наоборот.
Рис. 1. Группа вращений как гладкое многообразие (сфера): точки соответствуют начальному и конечному положениям объекта, проходящая по сфере кривая — траектории его движения
Вспомним теперь, что у нас все-таки не некоторое абстрактное многообразие, а группа; и у этой группы есть две операции: «умножение» и «взятие обратного элемента». Мы можем «действовать» этими операциями на «сфере». Например мы можем сделать т.н. «левый сдвиг на элемент g», домножив все точки на сфере слева на g, т.е. заменив каждый элемент a на g*a. Поскольку у нас группа, то это движение сохраняет нашу «сферу» в целом, но перемещает внутри нее отдельные отмеченные точки. Интуитивная интерпретация: раз у нас группа поворотов, то мы можем повернуть нашу сферу любым из этих поворотов.
Рис. 2. Действие группы на себе как поворот сферы
Если подобные операции группы на самой себе (умножение и обращение) не портят гладкости ранее заданных на ней кривых (являются гладкими отображениями сферы на себя), то подобная группа называется группой Ли. Все практически значимые группы движений являются именно группами Ли.
Следующее интересное наблюдение, которое мы можем сделать, состоит в том, что у гладких кривых на гладких многообразиях можно определить понятие скорости движения по кривой — касательного вектора. То есть в нашем случае движущегося объекта можно определить скорость вращения тела в любой момент времени, причем эта скорость будет векторной величиной. В дифференциальной геометрии есть теорема, утверждающая, что пространство всех возможных касательных векторов к кривым в заданной точке n-мерного многообразия является n-мерным же линейным пространством — касательной плоскостью в заданной точке многообразия. Например, скорость вращения тела можно определить осью вращения и угловой скоростью вращения. Если мы перемножим единичный вектор направления оси на скаляр угловой скорости, то получится вектор угловой скорости, направление которого задает ось, а длина — скорость вращения. Этот вектор и будет элементом этого касательного пространства к группе вращений. На иллюстрации я использую в качестве модели двумерную сферу, поэтому и касательное пространство там получается двумерной касательной плоскостью к этой сфере.
Рис. 3. Скорость вращения как касательный вектор к траектории движения объекта и касательная плоскость — как пространство всех возможных скоростей вращения объекта в выбранной точке
Однако в силу того, что касательная плоскость задается для конкретной точки многообразия, пока что мы определили «скорость вращения объекта» только для одной конкретной точки (конкретного положения объекта), а хотелось бы — для любого возможного положения. Тут-то и приходит на помощь характерное для групп Ли «гладкое действие многообразия на самого себя»: определив касательный вектор и касательную плоскость всего в одной точке многообразия (как правило, в единице), мы дальше можем передвинуть получившиеся вектор и плоскость в любую другую точку многообразия. Для этого нам, правда, придется зафиксировать какой-то конкретный способ, которым мы будем это делать, чтобы избежать неоднозначностей, и классический подход — это использовать уже упоминавшийся левый сдвиг, т.е. использовать домножение слева на g для того, чтобы посчитать касательный вектор и касательную плоскость в точке g. Этому легко дать очевидную интерпретацию: допустим, мы определили, что такое «вращение влево со скоростью 5 градусов в секунду» для объекта находящегося в положении A. Как определить «вращение объекта влево со скоростью 5 градусов в секунду» в другом положении Б? Для этого надо просто вначале дать объекту повернуться в старом положении, а затем (умножение слева) поместить объект в нужное место таким же поворотом, который привел бы неподвижный объект из положения А в Б. Подобная нотация, естественно подразумевает, что движения действуют справа налево: действие a*b соответствует действию b, после которого следует действие a. Таким образом, определив скорость вращения в одной точке можно доопределить понятие «скорости вращения» для всех точек пространства. Полученное векторное поле (математик добавит: левоинвариантное векторное поле) на группе Ли естественно ассоциировать с «просто» скоростью вращения, уже без уточнения в какой именно точке.
Рис. 4. Определенная в одной точке «скорость вращения» естественным образом доопределяется для всех точек группы вращений
Как я уже писал ранее, пространство всех возможных угловых скоростей в одной точке является трехмерным касательным пространством. Поскольку указанное построение работает для любых касательных векторов, то слова «в точке» получается убрать и здесь; то есть получается просто «пространство возможных угловых скоростей объекта», и это пространство является обычным линейным пространством всех мыслимых трехмерных векторов. Это пространство называется алгеброй Ли соответствующей данной группе Ли. Почему алгеброй? А потому что для этого пространства уже естественным образом определена операция сложения и умножения на скаляр (пространство линейно) и на нем всегда можно определенным несложным образом ввести специальную «операцию умножения» — скобку Ли со следующими свойствами:
- [x, y] является билинейной операцией относительно x и y;
- [x, x] = 0 для любого x;
- [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0 для любых x, y, z.
Для нашего простого случая, вдобавок, из пунктов 1 и 2 так же следует пункт:
- [x, y] = -[y, x] для любых x, y.
Применительно к нашему случаю группы вращений, алгеброй Ли, как мы уже поняли, является обычное трехмерное пространство векторов, а «умножением» в нем выступает хорошо всем знакомое векторное произведение.
Группы и алгебры Ли играют заметную роль в математике, поскольку алгебра Ли (линейное пространство), как правило, является намного более простым объектом, нежели исходная группа. Скажем, в нашем модельном примере исходная группа Ли была хитрым трехмерным бубликом, вкладываемым в шестимерное пространство, а алгебра Ли — уже обычное трехмерное пространство. Для исходных элементов группы Ли была определена только операция комбинирования вращений и она была не коммутативной, тогда как элементы алгебры Ли можно складывать между собой и умножать на скаляры. Но при этом алгебра Ли однозначно определяет соответствующую группу Ли и позволяет определять ее свойства (например, определять тип группы) через свойства алгебры Ли, которые, по большому счету, сводятся к размерности линейного пространства и матрице, описывающей скобку Ли через ее действие на базисных векторах. Однако для практических целей нам понадобится другое важное свойство.
Рассмотрим произвольную гладкую траекторию движения f (t) в нашей группе Ли. Как уже было сказано, ее можно продифференцировать, определив скорость движения 
в каждой из точек траектории. Возьмем теперь произвольный элемент x из алгебры Ли (произвольную угловую скорость для нашего модельного примера). Как ранее упоминалось, этот элемент соответствует гладкому векторному полю x (g) касательных векторов ко всем элементам g многообразия группы Ли.
Рассмотрим теперь следующее дифференциальное уравнение:
Другими словами — что будет, если мы стартуем с единичного преобразования в момент t=0 и будем после этого постоянно вращать наше тело с фиксированной угловой скоростью x? В дифференциальной геометрии и теории обыкновенных дифференциальных уравнений доказывается, что для любого наперед заданного элемента x из алгебры Ли это уравнение имеет единственное возможное решение f (x, t), которое называется интегральной кривой. Значение этой функции в момент времени t=1 показывает «как далеко мы уйдем» из начального положения за единицу времени при движении с фиксированной угловой скоростью x и называется экспоненциальным отображением алгебры Ли на группу Ли:
Операция экспоненцирования однозначно определена для всех элементов алгебры Ли и обладает целым рядом удобных свойств:
- Exp (0) = 1;
- Exp (-x) = (Exp (x))-1;
- Exp (n*x) = (Exp (x))n для целых n;
Но важнее всего то, что экспонента позволяет тривиально реконструировать упомянутую интегральную кривую f (x, t) движения с постоянной угловой скоростью f (x, t) = Exp (tx).
Причем эта кривая является геодезикой на исходном многообразии группы Ли и следовательно локально кратчайшей траекторией, соединяющей между собой точку 1 с любой другой точкой. С помощью левого сдвига этот результат можно тривиально обобщить для траектории движения между произвольными положениями a и b. Достаточно просто посчитать g=ab-1, найти такое x, для которого Exp (x) = g=ba-1, и тогда геодезикой, соединяющей a и b будет f (t) = a Exp (xt).
Ну и в общем случае геодезикой, соответствующей движению с постоянной скоростью x и проходящей через любой элемент g является f (t, x, g) = g Exp (xt).
Таким образом, экспоненцирование элементов алгебры Ли позволяет естественным образом определить оптимальные интерполяционные траектории в исходной группе Ли. Упомянутая при этом «обратная» операция, находящая для заданного элемента группы g соответствующую угловую скорость вращения x, как нетрудно догадаться, называется логарифмированием Exp (Ln (g)) = g.
Однако в отличие от экспоненты она, как правило, определена неоднозначно;, а для некоторых элементов группы логарифм может быть не определен вообще. Например, если группа Ли состоит из нескольких связных компонент (условно говоря, две сферы, а не одна), то интегральные кривые, очевидно, не могут покинуть компонент содержащий единичный элемент и логарифм для любых элементов, лежащих вне этого компонента, не определен. Физический смысл этого довольно тривиален — если мы рассматриваем, к примеру, группу вращений и зеркальных симметрий в трехмерном пространстве, то траектории, которая бы непрерывным образом перевела бы объект к его зеркальному отражению, просто не существует, а неоднозначность определения вращения связана с тем, что если объект непрерывно вращать, он регулярно будет возвращаться к одному и тому же положению.
Матричное экспоненцирование и логарифм
С практической точки зрения теперь важно отметить тот небольшой факт, что все практически используемые движения можно записать в виде действительных матриц того или иного вида. Например, группа вращений в трехмерном пространстве описывается матрицами 3×3 с единичным детерминантом, группа евклидовых движений (rigid body transformation) — матрицами 4×4 следующего вида:
Которые тоже имеют единичный детерминант и т.д. Соответствующие группы являются подгруппами общей Общей Линейной Группы GL (R, n) невырожденных матриц размерности nxn. Эта группа является группой Ли, и ей соответствует алгебра Ли gl (R, n), состоящая из всех матриц размерности nxn, скобкой Ли для которой является матричный коммутатор: [A, B]=AB-BA. И в этой алгебре естественно возникают операции матричного экспоненцирования и матричного логарифмирования, обозначаемые Exp и Ln соответственно. Прелесть этого факта состоит в том, что все прочие частные группы движений являются подгруппами этой группы Ли и им соответствуют линейные подпространства в алгебре gl (R, n). При этом они делят с более общей группой и скобку Ли, и операции матричного экспоненцирования, т.е. независимо от конкретной подгруппы движений, экспонента и логарифм определяются одинаково — через экспоненту и логарифм соответствующих матриц.
Помимо уже упоминавшихся общих свойств:
- Exp (0) = 1;
- Exp (-A) = (Exp (A))-1;
- Exp (n*A) = (Exp (A))n для целых n;
- f (x, g, t) = g Exp (tx) — геодезика, проходящая через g и соответствующая скорости x
у матричного экспоненциала есть ряд дополнительных полезных свойств; - Если AB=BA то Exp (A+B) = Exp (A) Exp (B);
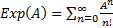(ряд Тейлора) причем этот ряд везде сходится; 
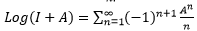(ряд Меркатора), сходится при |A|<1; 
; 
.
Эффективное вычисление матричной экспоненты и логарифма является сложной проблемой, и наиболее разумным подходом к его реализации является использование соответствующей математической библиотеки :).
Давайте посмотрим, как выглядят матрицы алгебр Ли для некоторых практически значимых групп. Например, наша простая группа вращений в матричном виде записывается как «все матрицы 3×3 с единичным детерминантом», а соответствующая ей алгебра Ли состоит из матриц 3×3 следующего вида:
Где (x, y, z) — это уже упоминавшийся вектор угловой скорости, определяющий скорость вращения по принципу «длина вектора = угловая скорость, направление = ось вращения». X, y и z здесь можно рассматривать как кинематический эквивалент углов Эйлера — по сути это угловые скорости вращения относительно осей x, y и z. Но в целом получаем просто другой способ записи вращений в представлении «ось и угол».
Если же мы рассматриваем случай произвольного движения в трехмерном пространстве, записывая его 4×4 матрицами вида 
, где R — это 3×3 матрица вращения, а T — это 3×1 вектор сдвига, то соответствующая алгебра Ли получается образованной из матриц:
Где (rx, ry, rz) имеет уже упомянутый смысл вектора угловой скорости, а (tx, ty, tz) — это вектор мгновенной скорости тела в точке (0,0,0). Соответствующие пары векторов называют мотором мгновенных скоростей твердого тела, и с их использованием связан изящный и сравнительно малоизвестный математический аппарат так называемого винтового исчисления, которое заслуживает отдельной статьи на Хабре.
Хотим добавить еще и масштабирование? Просто добавляем диагональные элементы (sx, sy, sz), соответствующие скорости «растягивания» по каждой из осей:
А вот для rigid body движения в 2D, которое можно задать матрицами 3×3 алгебра Ли получается из матриц:
…ну и так далее, думаю, идею вы уже уловили :). Но все-таки…
Зачем все это нужно?
Интерполяция
В качестве первого примера давайте возьмем простенькую 2D-фигуру и попытаемся ее передвинуть непрерывным движением из одного положения в другое. Параметризуем положение модели (x, y) и угол поворота (a), проводим линейную интерполяцию…
Все вроде работает, однако есть какая-то слабая, но явно уловимая неестественность движения. В чем же дело? Давайте нарисуем траектории, по которым движутся точки, расположенные поначалу в левой части экрана.
Нижняя часть, где находится наш самолетик, не слишком-то похожа на поворот: разные точки движутся не только с разной скоростью, но и по разным траекториям; однако самое странное происходит в верхнем левом углу, где точки совершают характерное возвратно-поступательное движение. Я не стал делать соответствующую иллюстрацию, поскольку на практике подобный артефакт встречается не очень часто, но думаю, что среди тех, кто занимается трехмерной анимацией, подобную штуку при интерполяции хотя бы пару раз наблюдали многие.
А что будет, если мы возьмем вместо этого экспоненту? Пусть A — это матрица исходного положения объекта, а B — матрица конечного положения. Положим положение объекта в момент времени t как 
, где 
.
Как видим, получился чистый плавный поворот, в котором все точки объекта движутся с постоянной скоростью. Конечно, такого же результата можно было бы добиться и не прибегая к экспоненте, а просто вспомнив, что любое движение на плоскости является либо параллельным переносом, либо вращением вокруг некоторой точки на некоторый угол. Достаточно было бы подобрать соответствующий центр вращения и поварьировать угол. Но прелесть экспоненты и логарифма состоит в том, что это абсолютный no-brainer, всего две-три строчки кода, которые с одинаковым успехом будут работать во всех обстоятельствах. Нужно интерполировать движение в 3D? Та же самая формула автоматически выдаст вам винт, даже если вы не знаете теорему Шаля. Нужно интерполировать линейное перемещение? Та же самая формула даст линейный переход. Интересным и полезным попутным свойством экспоненцирования как способа интерполяции является то, что при интерполировании перехода между элементами подгруппы экспонента «работает» сугубо внутри этой подгруппы. То есть если, к примеру, у вас в трехмерном пространстве есть робот, который может двигаться только в определенной плоскости, или, скажем, вращается относительно определенной точки, то интерполяция между двумя его положениями автоматически будет происходить только в этой же плоскости или вращением относительно этой точки.
Параметризация и аппроксимация
Другое полезное свойство вытекает из того, что правильно заданная Exp:
- всегда дает элемент интересующей нас группы движений;
- разлагается в ряд Тейлора.
Ну то есть, допустим, хотим мы найти матрицу вращения, которая будет наилучшим образом удовлетворять определенному требованию. Скажем, у нас есть два кусочка одной и той же поверхности, и мы хотим склеить их вместе, для чего подбираем матрицу вращения, которая наилучшим образом совместит первый кусочек со вторым. Чтобы реализовать поиск такой матрицы, нам вначале придется как-то параметризовать пространство этих матриц. Это можно сделать, к примеру, с помощью углов Эйлера, но когда мы подставим получившуюся матрицу с кучей синусов и косинусов, то будет непонятно как решать получившуюся оптимизационную проблему. Мы можем вместо этого попробовать использовать в качестве параметров для оптимизации непосредственно элементы самой матрицы движения; при этом получится куда более простая оптимизационная проблема (квадратичное уравнение в случае ICP), но нет никаких гарантий, что посчитанная таким образом матрица аффинного преобразования будет вращением. Существует несколько вариантов обхода этой проблемы: к примеру, в ряде работ предлагается считать афинную матрицу, а затем ортогонализировать ее до «ближайшего» вращения. Экспоненцирование дает один из интересных альтернативных вариантов. Как уже говорилось в начале, алгебра Ли является значительно более простым «аналогом» группы Ли (вращений), которая нас интересует. Поэтому:
- мы параметризуем элементы алгебры Ли (а это обычное линейное пространство);
- используем экспоненту чтобы вернуться к интересующей нас группе.
На первый взгляд может показаться, что этот подход еще хуже озвученной в начале параметризации углами Эйлера, поскольку матричную экспоненту в оптимизационной задаче считать еще неудобнее, чем синусы и косинусы. Однако для небольших движений вместо экспоненты мы можем просто записать ее разложение в ряд Тейлора:
Для мелких A этот ряд сходится очень быстро (для сколь угодно крупных он тоже сходится, но медленно), в силу чего его можно просто обрубить на первом-втором слагаемом после единичной матрицы. Например, чрезвычайно часто для малых углов используют приближение
Оно параметризует матрицу вращений хорошо известным всем приближением
Правда, обычно когда это приближение вводят, то не упоминают ни экспонент, ни ряда Тейлора :). Однако «ноги» у этого приближения растут именно из ряда Тейлора, и теперь вы знаете, как эту аппроксимацию без труда продолжить до 2, 3 и вообще какого угодно порядка для произвольных классов движений (а не только вращений). Кстати отсюда же растет хорошо известный OpenCV-стам частный случай для группы трехмерных вращений — формула вращения Родригеса.
Использование подобного рода аппроксимаций позволяет упростить оптимизационную задачу (например, свести ее опять же к квадратичной) и при этом не требует сомнительного перехода с решением задачи для афинных матриц и последующего проектирования результата на нужную группу. Единственным ее ограничением является требование к малости матрицы A, но как правило, обойти его достаточно просто. Достаточно просто параметризовать не непосредственно «матрицу положения объекта», а «матрицу движения, которое нужно применить к объекту». При условии, что объект изначально стоит более-менее где-то в правильном месте, необходимая матрица «подвижки» в целом классе задач получается достаточно маленькой. К примеру, хорошо этот подход работает в итерационных алгоритмах, поскольку шаг перемещения объектов на каждой последующей итерации в них, как правило, быстро уменьшается.
Вот такая вот простая, интересная и на удивление малоизвестная штука. А Вы используете матричные экспоненты и алгебры Ли в своих проектах :)?
Комментарии (2)
26 июля 2016 в 12:52
0↑
↓
Тогда уж добавьте список литературы:
«An Introduction to Physically Based Modeling», David Baraff
«Geometric tools for computer graphics», David H. Eberly
Catmull–Rom spline
www.gamasutra.com/view/feature/131313/advanced_character_physics.php
Опять эти ваши матаны без ничего вообще.Написали бы лучше какой-нибудь steering behavior. А то опять будут на собеседовании говорить «я слышал и читал», а сами сходу даже аишников для гоночек будут в интернете искать. Если как тестовое задание давать.
bfDeveloper
26 июля 2016 в 12:57
0↑
↓
Это охренительно круто! Сходу понятно не всё, но интерполяция это интересно.
Вопрос не совсем по теме, но давно интересовал. А следует ли из гладкости однозначность представления каждого поворота? В общем случае точно нет, а что здесь? В углах 360 == 0, что иногда неудобно. Имеется в виду, например, такая задача: есть анимация вращения колеса, промежуточные кадры интерполируются по клбчевым, но при переходе через 360 мы интерполируем углы 359 и 0, получая резкий скачок на одном кадре. Понятно, что это легко решается на программном уровне, приводя всё в один отрезок, по сути оперируя углом по модулю 360, но всё же решается ли эта проблема более элегантно?
