«Правда, чистая правда и статистика» или «15 распределений вероятности на все случаи жизни»30.09.2016 11:48

Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить токи над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.

В первую очередь, данный материал будет интересен студентам, изучающим теорию вероятностей и статистику, хотя и «зрелые» специалисты смогут его использовать в качестве справочника. В одной из следующих работ я покажу пример использования статистики для построения теста оценки значимости показателей биржевых торговых стратегий.

В работе будут рассмотрены дискретные распределения:

Бернулли;
биноминальное;
геометрическое;
Паскаля (отрицательное биноминальное);
гипергеометрическое;
Пуассона,

, а также непрерывные распределения:

Гаусса (нормальное);
хи-квадрат;
Стьюдента;
Фишера;
Коши;
экспоненциальное (показательное) и Лапласа (двойное экспоненциальное, двойное показательное);
Вейбулла;
гамма;
бета.

В конце статьи будет задан вопрос для размышлений. Свои размышления по этому поводу я изложу в следующей статье.

Некоторые из приведённых непрерывных распределений являются частными случаями распределения Пирсона.

Дискретные распределения
Дискретные распределения используются для описания событий с недифференцируемыми характеристиками, определёнными в изолированных точках. Проще говоря, для событий, исход которых может быть отнесён к некоторой дискретной категории: успех или неудача, целое число (например, игра в рулетку, в кости), орёл или решка и т.д.

Описывается дискретное распределение вероятностью наступления каждого из возможных исходов события. Как и для любого распределения (в том числе непрерывного) для дискретных событий определены понятия матожидания и дисперсии. Однако, следует понимать, что матожидание для дискретного случайного события — величина в общем случае нереализуемая как исход одиночного случайного события, а скорее как величина, к которой будет стремиться среднее арифметическое исходов событий при увеличении их количества.

В моделировании дискретных случайных событий важную роль играет комбинаторика, так как вероятность исхода события можно определить как отношение количества комбинаций, дающих требуемый исход к общему количеству комбинаций. Например: в корзине лежат 3 белых мяча и 7 чёрных. Когда мы выбираем из корзины 1 мяч, мы можем сделать это 10-ю разными способами (общее количество комбинаций), но только 3 варианта, при которых будет выбран белый мяч (3 комбинации, дающие требуемый исход). Таким образом, вероятность выбрать белый мяч: 3/10 (распределение Бернулли).

Следует также отличать выборки с возвращением и без возвращения. Например, для описания вероятности выбора двух белых мячей важно определить, будет ли первый мяч возвращён в корзину. Если нет, то мы имеем дело с выборкой без возвращения (гипергеометрическое распределение) и вероятность будет такова: (3/10) х (2/9) — вероятность выбрать белый мяч из начальной выборки умноженная на вероятность снова выбрать белый мяч из оставшихся в корзине. Если же первый мяч возвращается в корзину, то это выборка с возвращением (Биноминальное распределение). В этом случае вероятность выбора двух белых мячей составит (3/10) х (3/10).

наверх

Распределение Бернулли

(взято отсюда)

Если несколько формализовать пример с корзиной следующим образом: пусть исход события может принимать одно из двух значений 0 или 1 с вероятностями q и p соответственно, тогда распределение вероятности получения каждого из предложенных исходов будет называться распределение Бернулли:

$Bin_{p,q}\left(x\right)=\begin{cases}q,x=0\\ p, x=1\end{cases}$

По сложившейся традиции, исход со значением 1 называется «успех», а исход со значением 0 — «неудача». Очевидно, что получение исхода «успех или неудача» наступает с вероятностью p+q=1.

Матожидание и дисперсия распределения Бернулли:

$E\{Bin_{p,q}\}=p\ \ \ \ \left(1.1.2\right)$

$D\{Bin_{p,q}\}=pq=p\left(1-p\right)\ \ \ \ \left(1.1.3\right)$

наверх

Биноминальное распределение

(взято отсюда)

Количество k успехов в n испытаниях, исход которых распределен по Бернулли с вероятностью успеха p (пример с возвращением мячей в корзину), описывается биноминальным распределением:

$B_{n,p}(k)=C^n_kp^kq^{n-k}\ \ (1.2.1)$

где $C^n_k={n!\over{k!(n-k)!}}$ — число сочетаний из n по k.

По другому можно сказать, что биноминальное распределение описывает сумму из n независимых случайных величин, умеющих распределение Бернулли с вероятностью успеха n.
Матожидание и дисперсия:

$E\{B_{n,p}\}=np\ \ (1.2.2)$

$D\{B_{n,p}\}=npq\ \ (1.2.3)$

Биноминальное распределение справедливо только для выборки с возвращением, то есть, когда вероятность успеха остаётся постоянной для всей серии испытаний.

Если величины X и Y имеют биноминальные распределения с параметрами $%5C%7B%20n_x%2C%20p%20%5C%7D$ и $%5C%7B%20n_y%2C%20p%20%5C%7D$ соответственно, то их сумма также будет распределена биноминально с параметрами $%5C%7B%20n_x%2Bn_y%2C%20p%20%5C%7D$ .

наверх

Геометрическое распределение

(взято отсюда)

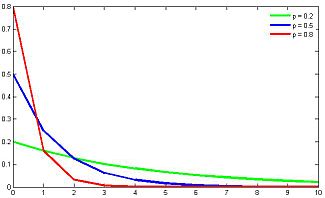
Представим ситуацию, что мы вытягиваем мячи из корзины и возвращаем обратно до тех пор, пока не будет вытянут белый шар. Количество таких операций описывается геометрическим распределением. Иными словами: геометрическое распределение описывает количество испытаний n до первого успеха при вероятности наступления успеха в каждом испытании p. Если n подразумевается номер испытания, в котором наступил успех, то геометрическое распределение будет описываться следующей формулой:

$Geom_p(n)=q^{n-1}p\ \ (1.3.1)$

Матожидание и дисперсия геометрического распределения:

$E\{Geom_p\}={1\over{p}}\ \ \ (1.3.2)$

$D\{Geom_p\}={q\over{p^2}}\ \ \ (1.3.3)$

Геометрическое распределение генетически связано с экспоненциальным распределением, которое описывает непрерывную случайную величину: время до наступления события, при постоянной интенсивности событий. Геометрическое распределение также является частным случаем отрицательного биноминального распределения.

наверх

Распределение Паскаля (отрицательное биноминальное рспределение)

(взято отсюда)

Распределение Паскаля является обобщением геометрического распределения: описывает распределение количества неудач k в независимых испытаниях, исход которых распределен по Бернулли с вероятностью успеха p до наступления r успехов в сумме. При r=1, мы получим геометрическое распределение для величины k+1.

$NB_{r,p}(k)=C^{k+r-1}_kp^rq^k\ \ (1.4.1)$

где С — число сочетаний.

Матожидание и дисперсия отрицательного биноминального распределения:

$E\{NB_{r,p}\}={rq\over{p}}\ \ \ (1.4.2)$

$D\{NB_{r,p}\}={rq\over{p^2}}\ \ \ (1.4.3)$

Сумма независимых случайных величин, распределённых по Паскалю, также распределена по Паскалю: пусть X имеет распределение $NB_%7Br_x%2Cp%7D$ , а Y — $NB_%7Br_y%2Cp%7D$ . Пусть также X и Y независимы, тогда их сумма будет иметь распределение $NB_%7Br_x%2Br_y%2Cp%7D$

наверх

Гипергеометрическое распределение

(взято отсюда)

До сих пор мы рассматривали примеры выборок с возвращением, то есть, вероятность исхода не менялась от испытания к испытанию.
Теперь рассмотрим ситуацию без возвращения и опишем вероятность количества успешных выборок из совокупности с заранее известным количеством успехов и и неудач (заранее известное количество белых и чёрных мячей в корзине, козырных карт в колоде, бракованных деталей в партии и т.д.).
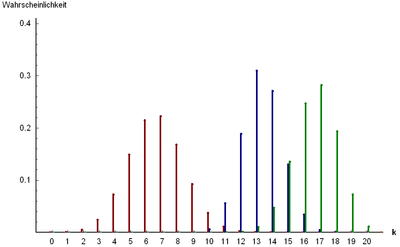
Пусть общая совокупность содержит N объектов, из них D помечены как »1», а N-D как »0». Будем считать выбор объекта с меткой »1», как успех, а с меткой »0» как неудачу. Проведём n испытаний, причём выбранные объектв больше не будут участвовать в дальнейших испытаниях. Вероятность наступления k успехов будет подчиняться гипергеометрическому распределению:

$HG_{N,D,n}(k)={C^D_kC^{N-D}_{n-k}\over{C^N_n}}\ \ (1.5.1)$

где С — число сочетаний.

Матожидание и дисперсия:

$E\{HG_{N,D,n}\}={nD\over{N}}\ \ (1.5.2)$

$D\{HG_{N,D,n}\}=n{D\over{N}}{N-D\over{N}}{N-n\over{N-1}}\ \ (1.5.3)$

наверх

Распределение Пуассона

(взято отсюда)

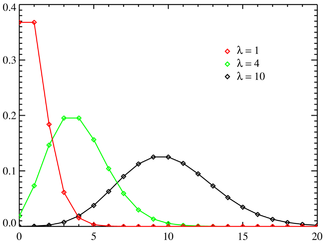
Распределение Пуассона значительно отличается от рассмотренных выше распределений своей «предметной» областью: теперь рассматривается не вероятность наступления того или иного исхода испытания, а интенсивность событий, то есть среднее количество событий в единицу времени.

Распределение Пуассона описывает вероятность наступления k независимых событий за время t при средней интенсивности событий $%5Clambda$ :

$P_{\lambda,t}(k)={\left(\lambda t\right)^k\over{k!}}e^{\lambda t}\ \ \ (1.6.1)$

Матожидание и дисперсия распределения Пуассона:

$E\{P_{\lambda,t}\}=\lambda t\ \ \ (1.6.2)$

$D\{P_{\lambda,t}\}=\lambda t\ \ \ (1.6.3)$

Дисперсия и матожидание распределения Пуассона тождественно равны.

Распределение Пуассона в сочетании с экспоненциальным распределением, описывающим интервалы времени между наступлениями независимых событий, составляют математическую основу теории надёжности.

наверх

Непрерывные распределения
Непрерывные распределения, в отличие от дискретных, описываются функциями плотности (распределения) вероятности f (x), определёнными, в общем случае, на некоторых интервалах.

Если известна плотность вероятности для величины х: f (x) и определено преобразование y=g (x), то плотность вероятности для y может быть получена автоматически:

$f_y(y)=f\left(g^{-1}(y)\right)\left|{dg^{-1}\over{dy}}(y)\right|\ \ \ (2.0.1)$

при условии дифференцируемости g (x).

Плотность вероятности h (z) суммы случайных величин x и y (z=x+y) с распределениями f (x) и g (y) описывается свёрткой f и g:

$h(z)=\int f(t)g(z-t)dt=(f*g)(z)\ \ \ (2.0.2)$

Если распределение суммы случайных величин принадлежит к тому же распределению, что и слагаемые, такое распределение называется бесконечно делимым. Примеры бесконечно делимых распределений: нормальное, хи-квадрат, гамма, распределение Коши.

Плотность вероятности h (z) произведения случайных величин x и y (z=xy) с распределениями f (x) и g (y) может быть вычислена следующим образом:

$h(z)=\int f(t)g(z/t)dt\ \ \ (2.0.3)$

Некоторые из приведённых ниже распределений являются частными случаями распределения Пирсона, которое, в свою очередь, является решением уравнения:

${df\over{dx}}(x)={a_0+a_1x\over{b_0+2b_1x+b_2x^2}}f(x)\ \ \ (2.0.4)$

где $a_i$ и $b_i$ — параметры распределения. Известны 12 типов распределения Пирсона, в зависимости от значений параметров.

Распределения, которые будут рассмотрены в этом разделе, имеют тесные взаимосвязи друг с другом. Эти связи выражаются в том, что некоторые распределения являются частными случаями других распределений, либо описывают преобразования случайных величин, имеющих другие распределения.

На приведённой ниже схеме отражены взаимосвязи между некоторыми из непрерывных распределений, которые будут рассмотрены в настоящей работе. На схеме сплошными стрелками показано преобразование случайных величин (начало стрелки указывает на изначальное распределение, конец стрелки — на результирующее), а пунктирными — отношение обобщения (начало стрелки указывает на распределение, являющееся частным случаем того, на которое указывает конец стрелки). Для частных случаев распределения Пирсона над пунктирными стрелками указан соответствующий тип распределения Пирсона.

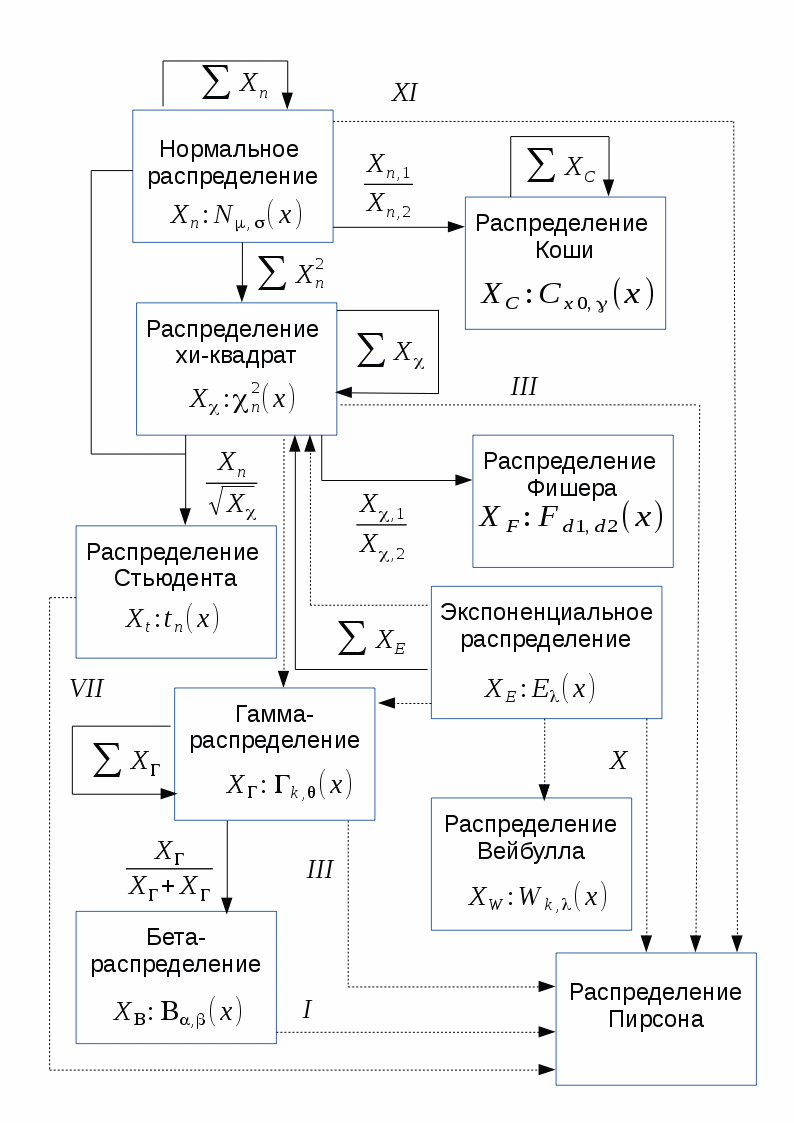
Предложенный ниже обзор распределений охватывает многие случаи, которые встречаются в анализе данных и моделировании процессов, хотя, конечно, и не содержит абсолютно все известные науке распределения.

наверх

Нормальное распределение (распределение Гаусса)

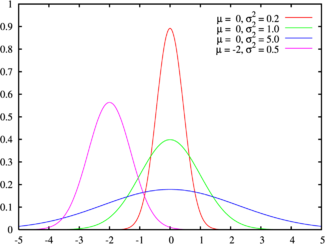
(взято отсюда)

Плотность вероятности нормального распределения $N_%7B%5Cmu%2C%5Csigma%7D(x)$ с параметрами $%5Cmu$ и $%5Csigma$ описывается функцией Гаусса:

$f(x)={1\over{\sigma \sqrt{2 \pi}}}e^{(x-\mu)^2\over{2\sigma^2}}\ \ \ (2.1.1)$

Если $%5Csigma%3D1$ и $%5Cmu%3D0$ , то такое распределение называется стандартным.

Матожидание и дисперсия нормального распределения:

$E\{N_{\mu,\sigma}\}=\mu\ \ \ (2.1.2)$

$D\{N_{\mu,\sigma}\}=\sigma^2\ \ \ (2.1.3)$

Область определения нормального распределения — множество натуральных чисел.

Нормальное распределение является распределение Пирсона типа VI.

Сумма квадратов независимых нормальных величин имеет распределение хи-квадрат, а отношение независимых Гауссовых величин распределено по Коши.

Нормальное распределение является бесконечно делимым: сумма нормально распределенных величин x и y с параметрами $%5C%7B%5Cmu_x%2C%5Csigma_x%5C%7D$ и $%5C%7B%5Cmu_y%2C%5Csigma_y%5C%7D$ соответственно также имеет нормальное распределение с параметрами $%5C%7B%5Cmu_%7Bx%2By%7D%2C%5Csigma_%7Bx%$ , где $%5Cmu_%7Bx%2By%7D%3D%5Cmu_x%2B%5Cmu_y$ и $%5Csigma_%7Bx%2By%7D%5E2%3D%5Csigma_x%5E$ .

Нормальное распределение хорошо моделирует величины, описывающие природные явления, шумы термодинамической природы и погрешности измерений.

Кроме того, согласно центральной предельной теореме, сумма большого количества независимых слагаемых одного порядка сходится к нормальному распределению, независимо от распределений слагаемых. Благодаря этому свойству, нормальное распределение популярно в статистическом анализе, многие статистические тесты рассчитаны на нормально распределенные данные.

На бесконечной делимости нормального распределении основан z-тест. Этот тест используется для проверки равенства матожидания выборки нормально распределённых величин некоторому значению. Значение дисперсии должно быть известно. Если значение дисперсии неизвестно и рассчитывается на основании анализируемой выборки, то применяется t-тест, основанный на распределении Стьюдента.

Пусть у нас имеется выборка объёмом n независимых нормально распределенных величин $X_i$ из генеральной совокупности со стандартным отклонением $%5Csigma$ выдвинем гипотезу, что $%5Cbar%7BX%7D%3D%5Cmu$ . Тогда величина $z={\bar{X}-\mu\over{\sigma \sqrt{n}}}$ будет иметь стандартное нормальное распределение. Сравнивая полученное значение z с квантилями стандартного распределения можно принимать или отклонять гипотезу с требуемым уровнем значимости.

Благодаря широкой распространённости распределения Гаусса, многие, не очень хорошо знающие статистику исследователи забывают проверять данные на нормальность, либо оценивают график плотности распределения «на глазок», слепо полагая, что имеют дело с Гауссовыми данными. Соответственно, смело применяя тесты, предназначенные для нормального распределения и получая совершенно некорректные результаты. Наверное, отсюда и пошла молва про статистику как самый страшный вид лжи.

Рассмотрим пример: нам надо измерить сопротивления набора резистров некоторого номинала. Сопротивление имеет физическую природу, логично предположить, что распределение отклонений сопротивления от номинала будет нормальным. Меряем, получаем колоколообразную функцию плотности вероятности для измеренных значений с модой в окрестности номинала резистров. Это нормальное распределение? Если да, то будем искать бракованные резистры используя тест Стьюдента, либо z-тест, если нам заранее известна дисперсия распределения. Думаю, что многие именно так и поступят.

Но давайте внимательнее посмотрим на технологию измерения сопротивления: сопротивление определяется как отношение приложенного напряжения к протекающему току. Ток и напряжение мы измеряли приборами, которые, в свою очередь, имеют нормально распределенные погрешности. То есть, измеренные значения тока и напряжения — это нормально распределенные случайные величины с матожиданиями, соответствующими истинным значениям измеряемых величин. А это значит, что полученные значения сопротивления распределены по Коши, а не по Гауссу.

Распределение Коши лишь напоминает внешне нормальное распределение, но имеет более тяжёлые хвосты. А значит предложенные тесты неуместны. Надо строить тест на основании распределения Коши или вычислить квадрат сопротивления, который в данном случае будет иметь распределение Фишера с параметрами (1, 1).

к схеме
наверх

Распределение хи-квадрат

(взято отсюда)

Распределение $%5Cchi%5E2$ описывает сумму n квадратов случайных величин $X_i$ , каждая из которых распределена по стандартному нормальному закону $N_%7B0%2C1%7D$ :

$\chi^2_n(x)={{\left(1\over 2 \right)}^{k\over 2}\over{\Gamma\left({k\over{2}}\right)}}x^{{k\over 2}-1}e^{-{x\over 2}}\ \ \ (2.2.1)$

где n — число степеней свободы, $x=\sum\limits_{i=1}^n {X^2_i}$ .

Матожидание и дисперсия распределения $%5Cchi%5E2$ :

$E\{\chi^2_n\}=n\ \ \ (2.2.2)$

$D\{\chi^2_n\}=2n\ \ \ (2.2.3)$

Область определения — множество неотрицательных натуральных чисел. $%5Cchi%5E2$ является бесконечно делимым распределением. Если x и y — распределены по $%5Cchi%5E2$ и имеют $n_x$ и $n_y$ степеней свободы соответственно, то их сумма также будет распределена по $%5Cchi%5E2$ и иметь $n_x%2Bn_y$ степеней свободы.

$%5Cchi%5E2$ является частным случаем гамма-распределения (а следовательно, распределением Пирсона типа III) и обобщением экспоненциального распределения. Отношение величин, распределенных по $%5Cchi%5E2$ распределено по Фишеру.

На распределении $%5Cchi%5E2$ основан критерий согласия Пирсона. с помощью этого критерия можно проверять достоверность принадлежности выборки случайной величины некоторому теоретическому распределению.

Предположим, что у нас имеется выборка некоторой случайной величины $X_i$ . На основании этой выборки рассчитаем вероятности $P_k$ попадания значений X в n интервалов (k=1: n). Пусть также есть предположение об аналитическом выражении распределения, в соответствие с которым, вероятности попадания в выбранные интервалы должны составлять $Q_k$ . Тогда величины $D_k%3DP_k-Q_k$ будут распределены по нормальному закону.

Приведем $D_k$ к стандартному нормальному распределению: $d_k%3D%7BD_k-m%5Cover%20S%7D$ ,
где $m={1\over n}\sum \limits_{i=1}^n {D_i}$ и $S=\sqrt {{1\over {n-1}}\sum \limits_{i=1}^n {D_i^2}}$ .

Полученные величины $d_i$ имеют нормальное распределение с параметрами (0, 1), а следовательно, сумма их квадратов распределена по $%5Cchi%5E2$ с n-1 степенью свободы. Снижение степени свободы связано с дополнительным ограничением на сумму вероятностей попадания значений в интервалы: она должна быть равна 1.

Сравнивая значение $z%3D%5Csum%20%5Climits_%7Bi%3D1%7D%5En%2$ с квантилями распределения $%5Cchi%5E2$ можно принять или отклонить гипотезу о теоретическом распределении данных с требуемым уровнем значимости.

к схеме
наверх

Распределение Стьюдента (t-распределение)

(взято отсюда)

Распределение Стьюдента используется для проведения t-теста: теста на равенство матожидания выборки стандартно нормально распределённых случайных величин некоторому значению, либо равенства матожиданий двух нормальных выборок с одинаковой дисперсией (равенство дисперсий необходимо проверять f-тестом). Распределение Стьюдента описывает отношение нормально распределённой случайной величины к величине, распределённой по хи-квадрат.

T-тест является аналогом z-теста для случая, когда дисперсия или стандартное отклонение выборки неизвестно и должно быть оценено на основании самой выборки.

Рассмотрим пример проверки равенства матожидания нормальной выборки некоторому значению: пусть нам дана выборка $X_i$ нормальных величин объёмом n из некоторой генеральной совокупности, выдвинем и проверим гипотезу о том, что матожидание этой совокупности равно m.

Рассчитаем величину $S%3D%7B%5Csum%20%5Climited_%7Bi%3D1%7D%5$ . Эта величина будет иметь распределение хи-квадрат. Тогда величина $t%3D%7B%7B%5Csum%20%5Climited_%7Bi%3D1%7$ будет иметь распределение Стьюдента $T_%7Bn-1%7D(x)$ c n-1 степенью свободы, где:

$T_{n}(x)={\Gamma \left({n+1 \over 2}\right) \over {\sqrt{n \pi}\Gamma \left({n \over 2}\right)\left(1+{x^2 \over n}\right)^{n+1 \over 2}}}\ \ \ (2.3.1)$

где Г (x) — гамма-функция Эйлера.

Полученное значение можно сравнивать с квантилями распределения Стьюдента и принимать либо отклонять гипотезу о равенстве маотожидания значению m с требуемым уровнем значимости.

Матожидание и дисперсия распределения Стьюдента:

$E\{T_{n}\}=0\ \ \ (2.3.2)$

$D\{T_{n}\}={n \over {n-2}}\ \ \ (2.3.3)$

при n>2.

к схеме
наверх

Распределение Фишера

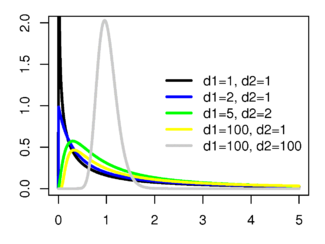
(взято отсюда)

Пусть X и Y независимые случайные величины, имеющие распределение хи-квадрат со степенями свободы $n_x$ и $n_y$ соответственно. Тогда величина $F%3D%7Bn_yX%20%5Cover%7Bn_xY%7D%7D$ будет иметь распределение Фишера со степенями свободы $(n_x%2Cn_y)$ , а величина $F%5E%7B-1%7D$ — распределение Фишера со степенями свободы $(n_y%2Cn_x)$ .
Распределение Фишера определено для действительных неотрицательных аргументов и имеет плотность вероятности:

$F_{n_1,n_2}(x)={\sqrt{ (n_1x)^{n_1}n_2^{n_2}\over {(n_1x+n_2)^{n_1+n_2}}} \over {xB\left({n_1 \over 2},{n_2 \over 2} \right)}}\ \ \ (2.4.1)$

Матожидание и дисперсия распределения Фишера:

$E\{F_{n_1,n_2}\}={n_2 \over {n_2-2}}\ \ \ (2.4.2)$

$D\{F_{n_1,n_2}\}={2n_2^2(n_1+n_2-2) \over {n_1(n_2-2)^2(n_2-4)}}\ \ \ (2.4.3)$

Матожидание определено для $n_2%3E2$ , а диспересия — для $n_2%3E4$ .

На распределении Фишера основан ряд статистических тестов, таких как оценка значимости параметров регрессии, тест на гетероскедастичность и тест на равенство дисперсий нормальных выборок (f-тест, следует отличать от точного теста Фишера).

F-тест: пусть имеются две независимые выборки $x_i$ и $y_j$ нормально распределенных данных объёмами $n_x$ и $n_y$ соответственно. Выдвинем гипотезу о равенстве дисперсий выборок и проверим её статистически.

Рассчитаем величину $F%3D%7Bn_y%20%5Csum%20%5Climited_%7Bi%3D$ . Она будет иметь распределение Фишера со степенями свободы $(n_x-1%2Cn_y-1)$ .

Сравнивая значение F с квантилями соответствующего распределения Фишера, мы можем принять или отклонить гипотезу о равенстве дисперсий выборок с требуемым уровнем значимости.

к схеме
наверх

Распределение Коши

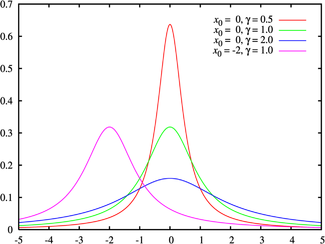
(взято отсюда)

Распределение Коши описывает отношение двух нормально распределенных случайных величин. В отличие от других распределений, для распределения Коши не определены матожидание и дисперсия. Для описания распределения используются коэффициенты сдвига $x_0$ и масштаба $%5Cgamma$ .

$C_{x_0,\gamma}(x)={1\over{\pi \gamma \left(1+\left({x-x_0\over {\gamma}} \right)^2 \right)}}\ \ \ (2.5.1)$

Распределение Коши является бесконечно делимым: сумма независимых случайных величин, распределённых по Коши, также распределена по Коши.

к схеме
наверх

Экспоненциальное (показательное) распределение и распределение Лапласа (двойное экспоненциальное, двойное показательное)

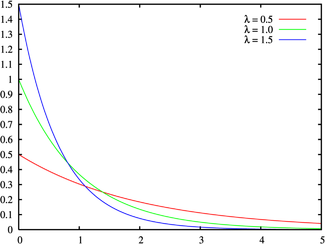
(взято отсюда)

Экспоненциальное распределение описывает интервалы времени между независимыми событиями, происходящими со средней интенсивностью $%5Clambda$ . Количество наступлений такого события за некоторый отрезок времени описывается дискретным распределением Пуассона. Экспоненциальное распределение вместе с распределением Пуассона составляют математическую основу теории надёжности.

Кроме теории надёжности, экспоненциальное распределение применяется в описании социальных явлений, в экономике, в теории массового обслуживания, в транспортной логистике — везде, где необходимо моделировать поток событий.

Экспоненциальное распределение является частным случаем распределения хи-квадрат (для n=2), а следовательно, и гамма-распределения. Так-как экспоненциально распределённая величина является величиной хи-квадрат с 2-мя степенями свободы, то она может быть интерпретирована как сумма квадратов двух независимых нормально распределенных величин.

Кроме того, экспоненциальное распределение является честным случаем распределения Вейбулла.

Дискретный вариант экспоненциального распределения — это геометрическое распределение.

Плотность вероятности экспоненциально распределения:

$E_\lambda(x)=\lambda e^{-\lambda x}\ \ \ (2.6.1)$

определена для неотрицательных действительных значений х.

Матожидание и дисперсия экспоненциального распределения:

$E\{E_\lambda\}={1 \over \lambda} \ \ \ (2.6.2)$

$E\{E_\lambda\}={1 \over \lambda^2} \ \ \ (2.6.3)$

Если функцию плотности вероятностей экспоненциального распределения отразить зеркально в область отрицательных значений, то есть, заменить х на |x|, то получится распределение Лапласа, также называемое двойным экспоненциальным или двойным показательным.

(взято отсюда)

Для большего обобщения, вводится параметр сдвига, смещающий центр «соединения» левой и правой частей распределения вдоль оси абсцисс. В отличие от экспоненциального, распределение Лапласа, определено на всей действительной числовой оси.

$L_{\alpha,\beta}(x)={\alpha \over 2}e^{-\alpha \left|x-\beta\right|} \ \ \ (2.6.4)$

где $%5Calpha$ — параметр масштаба, а $%5Cbeta$ — параметр сдвига.

Матожидание и дисперсия:

$E\{L_{\alpha, \beta}\}=\beta\ \ \ (2.6.5)$

$D\{L_{\alpha, \beta}\}={2 \over {\alpha^2}}\ \ \ (2.6.6)$

Благодаря более тяжёлым хвостам, чем у нормального распределения, распределение Лапласа используется для моделирования некоторых видов погрешностей измерения в энергетике, а также находит применение в физике, экономике, финансовой статистике, телекоммуникации и т.д.

к схеме
наверх

Распределение Вейбулла

(взято отсюда)

Распределение Вейбулла описывается функцией плотности вероятности следующего вида:

$W_{k, \lambda}(x)={k \over {\lambda}}\left({x \over {\lambda}}\right)^{k-1}e^{-\left({x \over {\lambda}}\right)^k}\ \ \ (2.7.1)$

где $%5Clambda$ ( $%5Clambda$ > 0)- интенсивность событий (аналогично параметру экспоненциального распределения), а k — показатель нестационарности (k > 0). При k = 1, распределение Вейбулла вырождается в экспоненциальное распределение, а в остальных случаях описывает поток независимых событий с нестационарной интенсивностью. При k > 1 моделируется поток событий с растущей со временем интенсивностью, а при k < 1 — со снижающейся. Область определения функции распределения плотности вероятностей: неотрицательные действительные числа.

Таким образом, распределение Вейбулла — обобщение экспоненциального распределения на случай нестационарной интенсивности событий. Используется в теории надёжности, моделировании процессов в технике, в прогнозировании погоды, в описании процесса измельчения и т.д.

Матожидание и дисперсия распределения Вейбулла:

$E\{W_{k, \lambda}\}=\lambda \Gamma\left(1 + {1 \over k} \right)\ \ \ (2.7.2)$

$D\{W_{k, \lambda}\}=\lambda^2 \left(\Gamma\left(1 + {2 \over k} \right ) - \Gamma\left(1 + {1 \over k} \right )^2\right)\ \ \ (2.7.3)$

где $%5CGamma(x)$ — гамма-функция Эйлера.

к схеме
наверх

Гамма-распределение (распределение Эрланга)

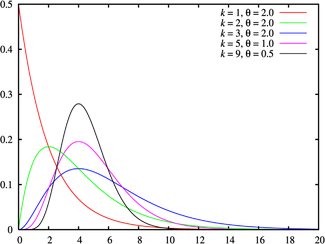
(взято отсюда)

Гамма-распределение является обобщением рапсределения хи-квадрат и, соответственно, экспоненциального распределения. Суммы квадратов нормально распределённых величин, а также суммы величин распределённых по хи-квадрат и по экспоненциальному распределению будут иметь гамма-распределение.

Гамма-распределение является распределением Пирсона III рода. Область определения гамма-распределения — натуральные неотрицательные числа.

Гамма-распределение определяется двумя неотрицательными параметрами k — число степеней свободы (при целом значении степеней свободы, гамма-распределение называется