Практика анализа данных в прикладной психологии

1. Вступление
Показан процесс анализа информации в сфере прикладной психологии. Если быть более точным, то я поделюсь своим опытом поиска различий между двумя группами людей. Будет показан один из самых популярных сценариев решения подобной задачи, а также приведены примеры исходного кода на языках программирования R и Python. Важно понимать, что вся изложенная информация является моим личным субъективным мнением.
2. Небольшая предыстория
Бывает так, что лучший результат показывают самые неожиданные метрики. Даже эксперты не всегда могут объяснить высокую важность подобных предикторов. Особенно ярко эта проблема проявляется в «расплывчатых понятиях прикладной психологии», таких как мотивация человека или его уверенность. Если говорить по существу вопроса, то речь идёт о необходимости решить задачу бинарной (дихотомической) классификации, а также выявить степень важности предикторов.
Несколько слов о планах. Во-первых, с помощью методов описательной статистики, визуального отображения и машинного обучения постараемся найти различия между двумя группами наблюдений. Во-вторых, увидим один из возможных сценариев поиска причин такой психологической проблемы, которую часто называют неуверенностью и отсутствием мотивации.
3. Первая попытка анализа данных
В задачах анализа поведенческих факторов очень много метрик подчинены закону распределения Гаусса (нормальное распределение). Особый интерес представляют не только те наблюдения, которые слабо отклоняются от математического ожидания, но и очень редкие наблюдения, расположенные за пределами трёх сигм. Дело в том, что в таких «крайних случаях» важные свойства могут проявляться наиболее ярко. Вообще, в прикладной психологии очень яркие проявления черт личности редко встречаются в популяции, но могут служить ключом к пониманию поведения большинства людей.
Любое очень детальное исследование поведения человека будет содержать немало сильно коррелирующих между собой предикторов. Можно сказать, что мультиколлинеарность — это привычное свойство таких наборов данных. Часто отмечается настолько выраженная линейная зависимость, что она может быть легко аппроксимирована простой линейной регрессией (методом наименьших квадратов). Даже гетероскедастичность относительно редкий спутник таких наборов. Тут хочется использовать метод главных компонент, чтобы сократить размерность. Вот только лучше всего использовать специальные методы предметной области, иначе мы рискуем потерять осмысленность данных.
Данные я заранее подготовил, объединив нужные метрики в четыре основных показателя. Но смысл этих данных я пока раскрывать не буду, по этой причине я выбрал для предикторов зашифрованные имена — латинское написание греческих букв. А пятая метрика будет выступать в роли метки класса наблюдения (0 или 1 — бинарная классификация). Как говориться, лёгким движением руки данные были экспортированы в стандартный файл формата CSV. Прежде всего, бегло посмотрим на них.
dataset.info()
'''
RangeIndex: 319 entries, 0 to 318
Data columns (total 5 columns):
alpha 319 non-null int64
beta 319 non-null int64
gamma 319 non-null int64
delta 319 non-null int64
class 319 non-null int64
dtypes: int64(5)
memory usage: 12.5 KB
'''Очевидно, что загрузка прошла успешно. Во всяком случае, структура данных ожидаемая. Посмотрим несколько случайно выбранных наблюдений. Глядя на эту небольшую выборку можно сделать два интуитивных предположения. Во-первых, представители обоих классов распределены приблизительно равномерно. Во-вторых, один из предикторов похож на возраст, а не на сложную составную метрику. Однако, по такому небольшому фрагменту данных делать серьёзные выводы будет опрометчиво.
dataset.sample(9)
'''
alpha beta gamma delta class
264 23 4932 3332 7429 1
216 31 4975 5541 3660 0
139 26 6686 4211 7729 1
18 23 4301 3063 3559 0
280 22 6043 2865 6491 0
212 25 7249 2974 3506 0
167 21 6929 6472 7203 1
272 29 5850 3576 7469 1
288 27 5382 4051 6413 1
'''Теперь взглянем на описательную статистику. Действительно, первый столбец очень сильно напоминает возраст. Даже минимальное значение (18 лет) смотрится как-то логично. Что касается других предикторов, то они очень тяжело интерпретируются. Обычно, чем больше показатель, тем выше у человека проявляется изучаемое качество или свойство личности. Но это пока пусть остаётся загадкой.
dataset.describe()
'''
alpha beta gamma delta class
count 319.000000 319.000000 319.000000 319.000000 319.000000
mean 29.416928 6451.351097 4556.492163 6127.012539 0.573668
std 7.498752 1725.993779 1524.070105 2113.231684 0.495320
min 18.000000 1930.000000 1805.000000 2624.000000 0.000000
25% 24.000000 5379.000000 3310.000000 4012.500000 0.000000
50% 28.000000 6405.000000 4327.000000 6237.000000 1.000000
75% 33.000000 7555.500000 5562.500000 7968.500000 1.000000
max 51.000000 10476.000000 8428.000000 9682.000000 1.000000
'''Попытаемся выстроить некоторую гипотезу о природе измерений. Распределение предполагаемого возраста похоже на результат подбора людей для исследования. Это создаёт интуитивное ощущение правильности предположения о смысле этого предиктора. Что касается понимания назначения других предикторов, то гистограмма нам не очень сильно помогла. Важно подчеркнуть, что категориальных (номинативных) и ранговых предикторов в этом наборе данных нет. Все числа были натуральными (целое и больше нуля). Пропущенных значений нет.
dataset.hist(bins = 20)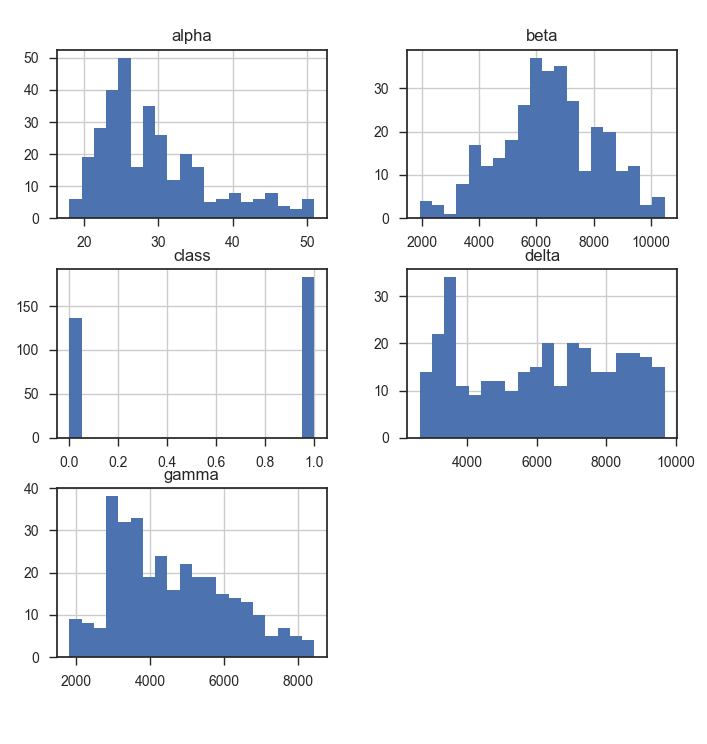
Очевидно, что один из предикторов сильно коррелирует с меткой наблюдения. Точнее, линейный коэффициент корреляции Карла Пирсона достаточно хорошо выделяется у двух предикторов, но один из них проявился особенно сильно.
sns.heatmap(dataset.corr(), square = True, annot = True)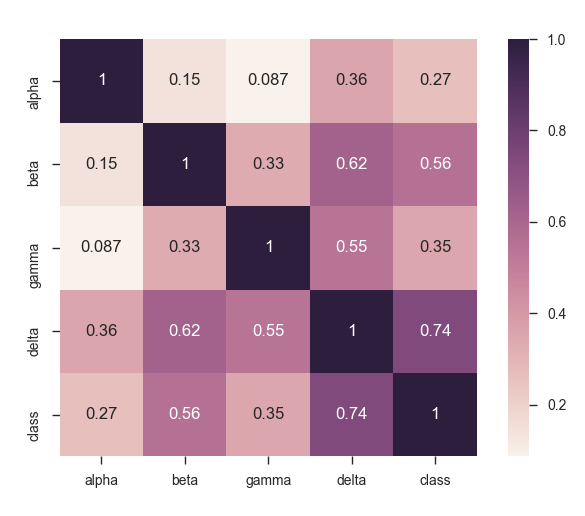
Вполне логично сравнить среднее значение или медиану у представителей разных классов. В данном конкретном наборе данных мы замечаем остро выраженное различие у «delta». На столько сильное, что проверять статистическую значимость нет особого смысла — всё очевидно.
dataset.groupby('class').median()
'''
alpha beta gamma delta
class
0 26.0 5656.5 3593.5 4176.0
1 29.0 7072.0 4825.0 7653.0
'''Пожалуй, нельзя обойти стороной ещё одну часто встречаемую ситуацию — разделение наблюдений на несколько кластеров. И различия у этих кластеров могут быть весьма значительными. Это необходимо учитывать, чтобы случайно не совершить ошибку «усреднения». Но сейчас нет такой ситуации.
pd.plotting.scatter_matrix(dataset, alpha = 0.2, diagonal = 'kde')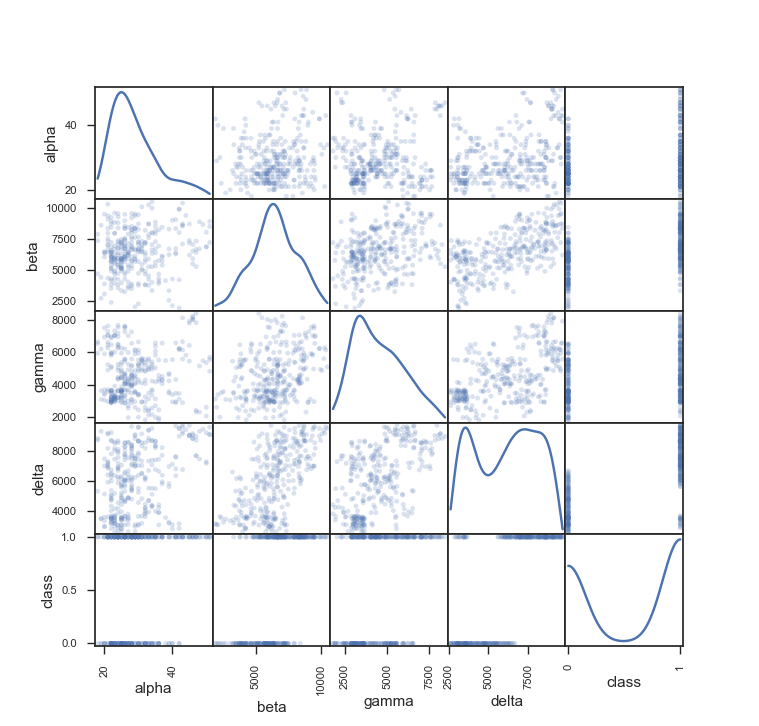
А теперь отобразим разными цветами представителей разных классов. Один из предикторов весьма информативен. Это для нас не сюрприз. Именно его медиана и среднее значение явно отличались у представителей разных классов. Судя по изображению может существовать такая гиперплоскость, которая с достаточно высокой точностью разделит классы. Линейная сепарабельность очень часто встречается у наборов данных поведенческих факторов, что делает возможным использовать быстрый алгоритм логистической регрессии.
sns.pairplot(dataset, kind = 'reg', hue = 'class', size = 2)
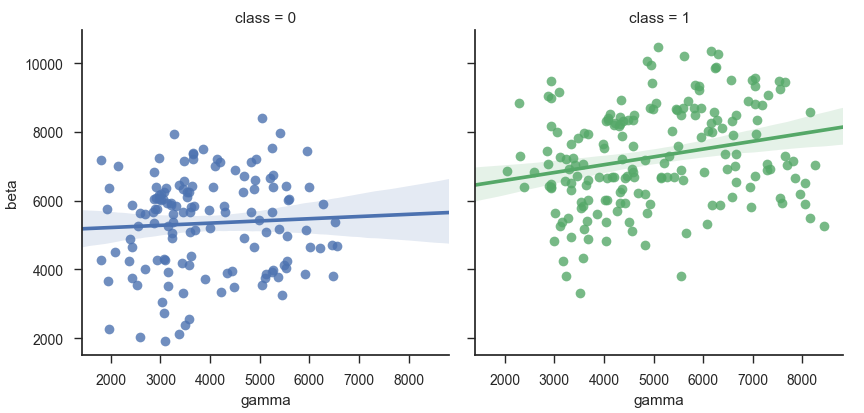
Ещё немножко субъективного мнения: лично мне удобнее искать зависимости или различия (либо факт их отсутствия), если классы отображены в разных столбцах. Например, у показанных ниже предикторов явно нет взаимосвязи, но есть очень слабая разница в значении (некоторые «зелёные» чуть больше).
sns.lmplot(
x = 'gamma',
y = 'beta',
hue = 'class',
col = 'class',
data = dataset,
)
А теперь можно приступать к стадии применения алгоритмов машинного обучения. В процессе предварительного изучения данных мы заметили, что категориальных (номинативных) предикторов нет, следовательно, нет смысла использовать для их преобразования One-hot encoding. Так как мы планируем использовать алгоритмы на основе ансамблей (комитетов) деревьев решений, то выполнять масштабирование (нормализацию) тоже нет смысла. Все значения в правильном формате и нет пропущенных данных. Таким образом, наши данные не требуют какой-либо подготовки.
4. Решение задачи с помощью машинного обучения
Напомню суть задачи. Было проведено исследование психологии поведения людей, в рамках которого были собраны необходимые измерения. Исследователям заранее известно к каком классу принадлежит человек. А классов получилось строго два — факт наличия или отсутствия изучаемой проблемы. Теперь исследователей интересуют два вопроса. Во-первых, можно ли вообще по собранным данным достаточно точно выявить проблему? Во-вторых, какие предикторы оказывают влияние на результат, а какие нет?
Первым делом попробуем алгоритм машинного обучения Random Forest. Это объясняется очень просто: он не требует детальную предварительную настройку, хорошо работает с данными разной природы и способен автоматически выявить степень важности предикторов. Обратим внимание, что размер входной матрицы достаточно умеренный, следовательно, можно смело указывать большое количество глубоких деревьев и не бояться слишком долгой работы. А вот процесс подбора количества предикторов (ограничение для деревьев) уже более творческая составляющая. Разрешим каждому дереву использовать все предикторы.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.ensemble import RandomForestClassifier
sns.set(style = 'ticks', color_codes = True)
dataset = pd.read_csv(DATASET_FILE_URL)
class_label = dataset.pop('class')
X, Xt, y, yt = train_test_split(dataset, class_label, test_size = .5)
model = RandomForestClassifier(
n_estimators = 1000,
max_depth = 100,
max_features = 4
).fit(X, y)
print(classification_report(yt, model.predict(Xt)))
pd.Series(model.feature_importances_, index = Xt.columns).plot(kind = 'barh')
plt.show()
'''
precision recall f1-score support
0 0.91 0.88 0.89 77
1 0.89 0.92 0.90 83
avg / total 0.90 0.90 0.90 160
'''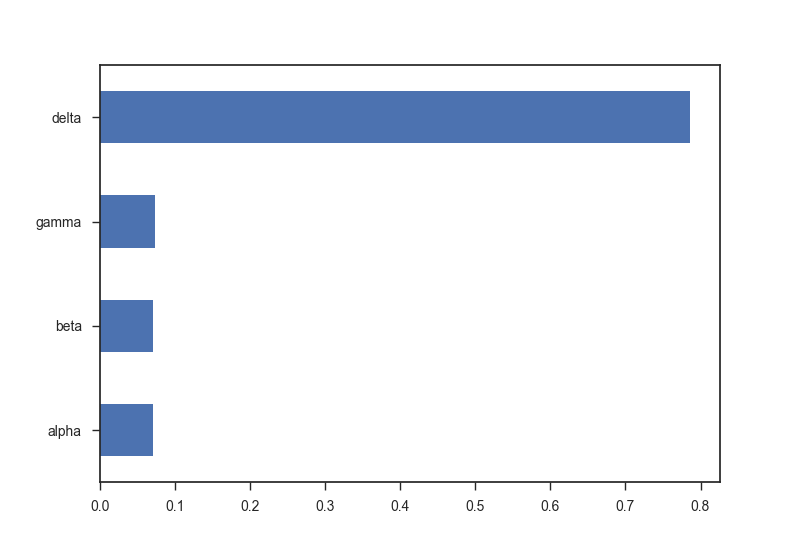
Такой результат нас полностью устраивает. Мы получили подходящий уровень точности, а также узнали степень важности предикторов. Наше мнение подтвердилось — как в старом детективе мы нашли самого главного виновника проблемы.
Ради интереса попробуем и другие алгоритмы машинного обучения, которые способны показать степень важности предикторов. Например, пару дней назад я столкнулся с «более сырым» набором данных, в котором было 55 предикторов, а 40 из них были номинативными. Тогда лучше всего показал себя CatBoost. Мы можем попробовать и его на этом наборе данных, где, кстати, вообще нет номинативных предикторов.
from catboost import CatBoostClassifier
model = CatBoostClassifier().fit(X, y)
print(classification_report(yt, model.predict(Xt)))
pd.Series(model.feature_importances(Xt, yt), index = Xt.columns)
'''
precision recall f1-score support
0 0.87 0.90 0.89 73
1 0.92 0.89 0.90 87
avg / total 0.89 0.89 0.89 160
alpha 15.971408
beta 16.231243
gamma 15.809242
delta 51.988106
'''Обратите внимание, что я предварительно не выбирал оптимальные гиперпараметры. Использовал его сразу, как вынул из коробки. Для сравнения проделаю аналогичную операцию с XGBoost. Также без предварительной настройки:
import xgboost as xgb
model = xgb.XGBClassifier().fit(X, y)
print(classification_report(yt, model.predict(Xt)))
importance = model.booster().get_score(importance_type = 'gain')
pd.Series(list(importance.values()), index = importance.keys())
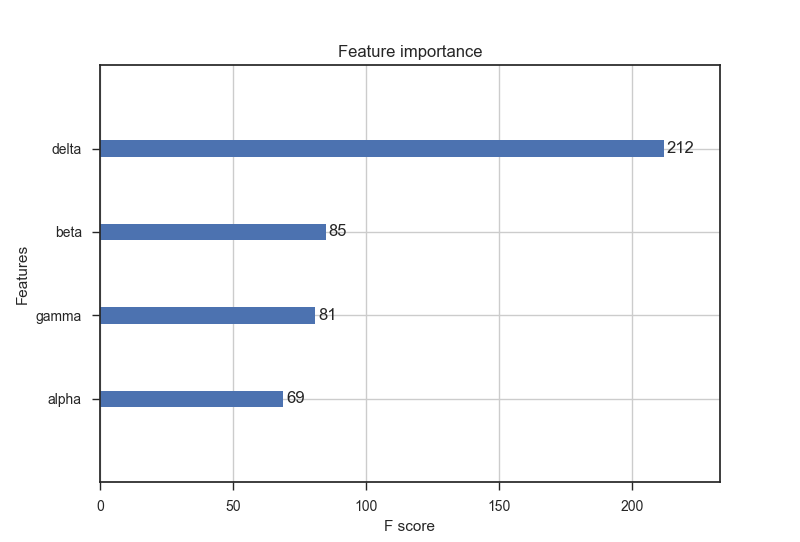
xgb.plot_importance(model)
plt.show()
'''
precision recall f1-score support
0 0.88 0.92 0.90 73
1 0.93 0.90 0.91 87
avg / total 0.91 0.91 0.91 160
delta 3.711117
alpha 1.101336
gamma 0.879750
beta 0.659535
'''
Ещё на этапе изучения данных было видно, что линейная сепарабельность возможна, значит, попробуем и логистическую регрессию:
from sklearn.linear_model import LogisticRegression
model = LogisticRegression().fit(X, y)
print(classification_report(yt, model.predict(Xt)))
pd.Series(model.coef_[0], index = Xt.columns)
'''
precision recall f1-score support
0 0.92 0.74 0.82 73
1 0.81 0.94 0.87 87
avg / total 0.86 0.85 0.85 160
alpha -0.085451
beta -0.000115
gamma -0.000402
delta 0.000956
'''Кроме этого, в задачах анализа поведенческих факторов часто используется алгоритм ближайших соседей. Это связано с тем, что расстояние (например, евклидова метрика) между двумя векторами похожих людей будет близким. Логично предположить, что люди одной группы набирают похожее количество баллов, возможно, формируя несколько кластеров. Напомню, что kNN относится к той категории алгоритмов, которая не умеет показывать степень важности предикторов. В небольших наборах данных можно вручную удалить «подозреваемого», чтобы посмотреть на качество обучения модели без него.
Алгоритм ближайших соседей весьма чувствителен к разной природе данных (и к выбросам), следовательно, аналогично алгоритмам на основе нейронных сетей или методу опорных векторов требует предварительную нормализацию. Именно с неё мы и начнём.
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
scaler = StandardScaler()
X = scaler.fit_transform(X)
Xt = scaler.fit_transform(Xt)
model = KNeighborsClassifier(n_neighbors = 7).fit(X, y)
print(classification_report(yt, model.predict(Xt)))
'''
precision recall f1-score support
0 0.88 0.82 0.85 73
1 0.86 0.91 0.88 87
avg / total 0.87 0.87 0.87 160
'''Хочется ещё немного поэкспериментировать. Посмотрим на результат работы алгоритма на основе нейронных сетей.
import tensorflow as tf
def get_train_inputs():
xr = tf.constant(X)
yr = tf.constant(y)
return xr, yr
def get_test_inputs():
xr = tf.constant(Xt)
yr = tf.constant(yt)
return xr, yr
model = tf.contrib.learn.DNNClassifier(
feature_columns = [tf.contrib.layers.real_valued_column('', dimension = 4)],
hidden_units = [10, 20, 10],
n_classes = 2,
model_dir = 'tmp_dir_tensorflow'
).fit(input_fn = get_train_inputs, steps = 8000)
predictions = list(model.predict(input_fn = get_test_inputs))
print(classification_report(yt, predictions))
'''
precision recall f1-score support
0 0.91 0.84 0.87 73
1 0.87 0.93 0.90 87
avg / total 0.89 0.89 0.89 160
'''В итоге было выявлено, что по представленному вектору можно с высокой степенью точности назвать правильный класс наблюдения. Наиболее значимым был только один предиктор. Хочу обратить внимание, что мы успешно решили задачу без понимания смысла предикторов. Сейчас ещё не время раскрывать все карты. Ответ нас ждёт только во время повторного анализа данных.
5. Повторный анализ данных
Попробуем решить нашу задачу средствами языка программирования R. На этот раз мы уделим значительно больше внимания предметной области. Если при первом анализе данных мы смотрели на задачу глазами математика-программиста, то сейчас нам предстоит кардинально сменить амплуа. Я же не зря упоминал, что хочу поделиться своим многолетним опытом анализа именно поведенческих факторов.
Сейчас попробуем разрушить множество мифов о мотивации и уверенности. Эх, как наивно написал. А начнём мы анализ с очень предсказуемой операции — загрузим данные из файла и посмотрим на их структуру. На этом этапе мы убедимся, что формальные признаки правильной очистки и подготовки данных присутствуют. Из примера видно, что структура ожидаемая:
dataset <- read.csv(file = '1.csv', header = TRUE, sep = ',')
str(dataset)'data.frame': 319 obs. of 5 variables:
$ alpha: int 18 28 30 27 29 30 31 50 27 47 ...
$ beta : int 7344 6888 6694 5211 9466 3759 7010 6852 6345 6650 ...
$ gamma: int 6655 7281 5279 3988 2939 2426 4099 2045 4356 7852 ...
$ delta: int 8697 8178 7006 4856 6952 3113 3176 7262 6676 8688 ...
$ class: num 1 1 1 0 1 0 0 1 1 1 ...Чтобы проверить правильность загрузки посмотрим первые несколько наблюдений:
head(dataset, 5) alpha beta gamma delta class
1 18 7344 6655 8697 1
2 28 6888 7281 8178 1
3 30 6694 5279 7006 1
4 27 5211 3988 4856 0
5 29 9466 2939 6952 1
'Узнаем, сбалансированная ли выборка?
table(dataset$class) 0 1
136 183Раскрываю первый секрет: предиктор «alpha» — это действительно возраст, который не очень ценный для нас показатель. В исследовании принимали участия люди от 18 лет и до 51 года. Вспомним ещё раз описательную статистику:
summary(dataset) alpha beta gamma delta class
Min. :18.00 Min. : 1930 Min. :1805 Min. :2624 Min. :0.0000
1st Qu.:24.00 1st Qu.: 5379 1st Qu.:3310 1st Qu.:4012 1st Qu.:0.0000
Median :28.00 Median : 6405 Median :4327 Median :6237 Median :1.0000
Mean :29.42 Mean : 6451 Mean :4556 Mean :6127 Mean :0.5737
3rd Qu.:33.00 3rd Qu.: 7556 3rd Qu.:5562 3rd Qu.:7968 3rd Qu.:1.0000
Max. :51.00 Max. :10476 Max. :8428 Max. :9682 Max. :1.0000Первое объяснение проблемы «неуверенность и мотивация», которое приходит на ум — это последствия неправильного воспитания. Предиктор «beta» измеряет определённые ошибки воспитания (тревожное, унижающие, с обилием гиперопеки). Факт неполной семьи или «слабой роли отца в семье» также учитывается этой метрикой. Посмотрите на его корреляцию с другими предикторами и с меткой класса:
cor(dataset) alpha beta gamma delta class
alpha 1.0000000 0.1456241 0.0867106 0.3604732 0.2655922
beta 0.1456241 1.0000000 0.3337878 0.6225855 0.5552905
gamma 0.0867106 0.3337878 1.0000000 0.5467973 0.3541250
delta 0.3604732 0.6225855 0.5467973 1.0000000 0.7417065
class 0.2655922 0.5552905 0.3541250 0.7417065 1.0000000Но сильнее всего коррелирует с меткой класса вовсе не «beta», а «delta». Следовательно, если данные достаточно полно отражают реальную картину мира (репрезентативная выборка и правильный процесс сбора информации), то можно высказать предположение о том, что воспитание не самый значимый показатель, но безусловно очень важный. Теперь вспомним различия:
aggregate(. ~ class, dataset, median) class alpha beta gamma delta
1 0 26 5656.5 3593.5 4176
2 1 29 7072.0 4825.0 7653Воспользуемся уже знакомым приёмом, чтобы понять зависимость и визуально найти различия. Чтобы лучше осознать изображение необходимо рассматривать его небольшие части, а потом переключать своё внимание на общий план. Так нужно сделать несколько раз, чтобы значительно повысить точность восприятия. К сожалению, большинство информации, которую вы видите дорисовал мозг.
pairs(dataset, col = factor(dataset$class))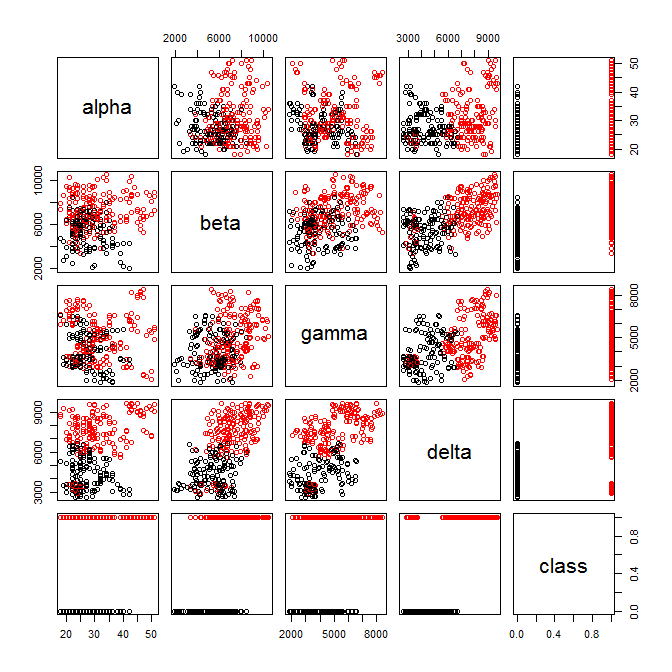
Естественно, для понимания распределения той или иной случайной величины мы обязательно посмотрим гистограмму распределения с указанием количества сегментов. Для сохранения разумного числа картинок я покажу только один пример. Отобразить гистограмму можно как встроенными средствами языка программирования R…
hist(dataset$alpha, col = 'red', breaks = 30)
… так и воспользоваться популярными библиотеками:
library(ggplot2)
ggplot(data = dataset, aes(dataset$alpha)) +
geom_histogram(bins = 30)
Кстати, это очень удобная библиотека с огромным функционалом. Ряд книг и официальная документация подробно описывают все необходимые возможности. Для примера я покажу уже ранее упомянутый метод разделения представителей разных классов на два столбца:
ggplot(dataset, aes(x = alpha, y = beta, color = factor(class))) +
geom_point(shape = 1) +
geom_smooth(method = lm) +
facet_grid(. ~ class)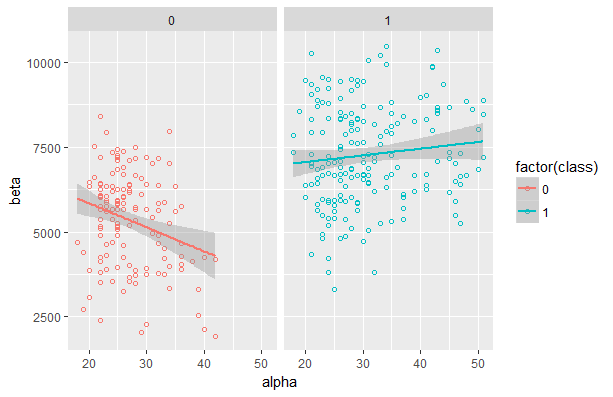
После предварительного изучения данных самое время воспользоваться алгоритмами машинного обучения. Прежде всего, я хочу посмотреть на результат работы алгоритма Random Forest. Обратите внимание, что я не ограничивал размер деревьев, но указал ограничение на количество предикторов (их 2), по которым будет строится каждое дерево. Ещё я указал, что мне нужно построить 1000 деревьев.
library(randomForest)
model.classification <- randomForest(
as.factor(class) ~ .,
data = dataset,
importance = TRUE,
mtry = 2,
do.trace = FALSE,
ntree = 1000
)
model.classification$confusion
model.classification$importance
varImpPlot(model.classification) 0 1 class.error
0 128 8 0.05882353
1 20 163 0.10928962
0 1 MeanDecreaseAccuracy MeanDecreaseGini
alpha 0.02330505 0.01945604 0.02098099 11.57448
beta 0.03914996 0.02020077 0.02812746 29.90205
gamma 0.02095899 0.02036658 0.02044420 17.96225
delta 0.35067468 0.27116144 0.30348320 95.93535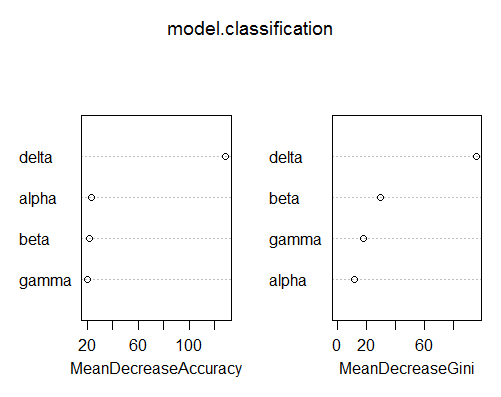
В завершении ещё раз посмотрим на степень значимости предикторов. Теперь уже с помощью алгоритма логистической регрессии, который встроен в язык программирования R. Коэффициенты логистической регрессии помогают выявить важные предикторы (звёздочки рядом отображают значимость).
glmr = glm(formula = class ~ ., data = dataset, family = binomial)
summary(glmr)Call:
glm(formula = class ~ ., family = binomial, data = dataset)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.7095 -0.4698 0.1224 0.3984 2.7434
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.124e+00 1.422e+00 -6.415 1.41e-10 ***
alpha 3.189e-02 3.396e-02 0.939 0.3477
beta 4.510e-04 1.445e-04 3.121 0.0018 **
gamma -9.367e-05 1.563e-04 -0.599 0.5490
delta 1.051e-03 1.448e-04 7.257 3.97e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 435.28 on 318 degrees of freedom
Residual deviance: 203.03 on 314 degrees of freedom
AIC: 213.03
Number of Fisher Scoring iterations: 6В итоге мы смогли в автоматическом режиме найти самую важную метрику, знание которой позволяет с огромной вероятностью правильно выявить проблему. Конечно, поведенческие факторы почти всегда требуют серию экспериментов. Нужно помнить, что высокую эффективность могут показать весьма неожиданные подходы, о которых исследователям сложно догадаться.
А вот и обещанное описание предикторов:
- alpha — число полных лет по паспортным данным.
- beta — результат ответа на 35 вопросов (у разных вопросов разное количество баллов), предназначенных для выявления различных ошибок воспитания. Чем выше значение метрики, тем более остро выражена проблема.
- gamma — объединение результатов тестов, которые субъективно оцениваются как малодостоверные (цвета, изображения, логика).
- delta — результат ответа на 48 вопросов о различных психологических травмах, которые гипотетически должны быть ограничивающим фактором.
Таким образом, если мы будем считать этот набор данных достоверным (если были выполнены два условия: репрезентативная выборка и правильная методика сбора данных), то можно сделать вывод о значимости психологических травм. Именно такие травмы формируют у человека страх, следовательно, человек не готов предпринимать действительно продуктивных попыток менять свою жизнь. А где нет многократных, продуманных и настойчивых попыток, там нет и результатов. Отсутствие желаемых результатов — это внешнее подкрепление своих комплексов, которое снижает самооценку. И так циклически повторяется.
Разумеется, человеческая психика находит некий коридор стабильности или зону комфорта. Выбирается такое состояние не случайным образом, а в соответствии с убеждениями человека. Любопытно и другое наблюдение — изменение убеждений происходит после получения результатов в жизни человека. Очень важно понимать, что мозг учитывает только собственные результаты (например, спортивные достижение и хорошая заработная плата), но не примеры других людей.
6. Выводы
Психология прочно ассоциируется с чем угодно, только не с математикой или программированием. Однако, эпоха умозрительных заключений постепенно проходит. Современные технологии могут собрать и обработать огромное количество показателей, что позволяет делать выводы не интуитивно, а на основании конкретных фактов.
