Поверхность по сети кривых27.12.2022 15:16

Продолжаем серию постов о сложной математике, которую невозможно описать простыми словами. В этот раз мы поговорим о функционале поверхностного моделирования в геометрическом ядре C3D Modeler — поверхности по сети кривых.

Заранее предупреждаем. Дальше вам встретится множество геометрических терминов и формул. А кто говорил, что будет легко?!

О различных аспектах построения поверхности по сети кривых, а также полезных для ее практической реализации тонкостей, рассказывает Павел Егоров, математик-программист в C3D Labs.

Поверхность по сети кривых является ценным инструментом в инженерном проектировании геометрических объектов со сложными обводами. Она образуется двумя семействами кривых, которые, взаимно пересекаясь, образуют сетку фрагментов, имеющую матричную структуру. Помимо точного прохождения через ее образующие кривые поверхность по сети кривых также позволяет задавать для них значения производных, что оказывается очень полезным для обеспечения различных типов граничных условий. На рисунке 1 показана поверхность, построенная по двум кривым в каждом направлении и использующая данное свойство для обеспечения касательного сопряжения с другой поверхностью.

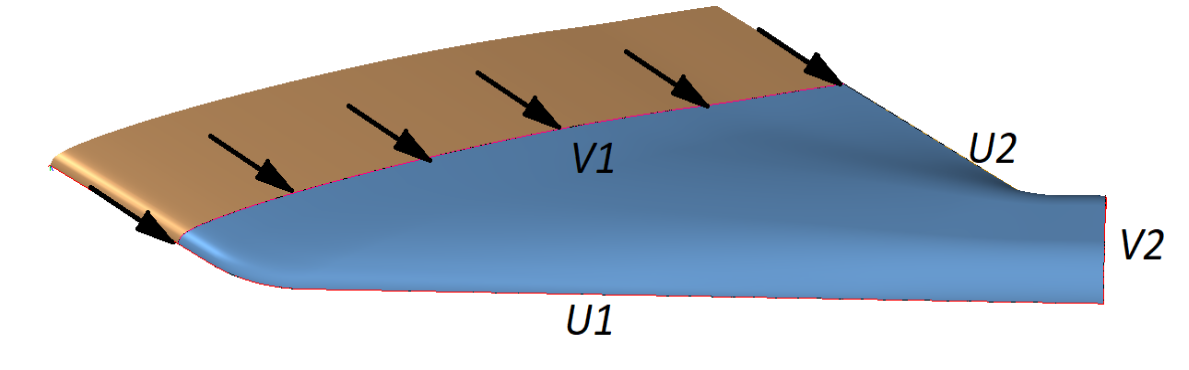Рисунок 1. Поверхность по сети кривых Рисунок 1. Поверхность по сети кривых

Два семейства образующих кривых задают соответствующие параметрические изолинии на получаемой поверхности. Так, образующие из семейства u-кривых задают на поверхности изолинии с постоянным параметром v=const, а образующие из семейства v-кривых — изолинии с постоянным параметром u=const. Каждая клетка или патч поверхности по сети кривых описывается формой Кунса, которую можно упрощенно записать в виде

r(u,v)=H_u (u,v)+H_v (u,v)+M(u,v) (1)

Первые два слагаемых в формуле (1) представляют собой формы Эрмита по каждому направлению. Каждая форма Эрмита обеспечивает прохождение поверхности через опорные кривые трансверсального направления. Так, кубическая форма Эрмита по u направлению обеспечивает прохождение через кривые v-семейства (рисунок 2),

Рисунок 2. Форма Эрмита в направлении u обеспечивает прохождение через v-кривые Рисунок 2. Форма Эрмита в направлении u обеспечивает прохождение через v-кривые

а форма Эрмита по v направлению обеспечивает прохождение через кривые u-семейства (рисунок 3).

Рисунок 3. Форма Эрмита в направлении v обеспечивает прохождение через u-кривые Рисунок 3. Форма Эрмита в направлении v обеспечивает прохождение через u-кривые

Кубические формы Эрмита задаются в виде

$\begin{array}{l} {H_u}(u,v) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {{V_1}(v)}\\ {{V_2}(v)}\\ {{V_{u1}}(v)}\\ {{V_{u2}}(v)} \end{array}} \right] = \underline H (u) \cdot \left[ {\begin{array}{*{20}{c}} {{V_1}(v)}\\ {{V_2}(v)}\\ {{V_{u1}}(v)}\\ {{V_{u2}}(v)} \end{array}} \right]\\ {H_v}(u,v) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(v)}&{{\alpha _2}(v)}&{{\beta _1}(v)}&{{\beta _2}(v)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {{U_1}(u)}\\ {{U_2}(u)}\\ {{U_{v1}}(u)}\\ {{U_{v2}}(u)} \end{array}} \right] = \underline H (v) \cdot \left[ {\begin{array}{*{20}{c}} {{U_1}(u)}\\ {{U_2}(u)}\\ {{U_{v1}}(u)}\\ {{U_{v2}}(u)} \end{array}} \right] \end{array}, (2)$

где α1, α2, β1, β2— функции Эрмита, определенные на рассматриваемом диапазоне параметров;

U1(u), U2(u), V1(v), V2(v) — опорные кривые, ограничивающие патч поверхности;

Uv1(u), Uv2(u), Vu1(v), Vu2(v) — «поток» первой производной через границы патча.

Для простоты изложения здесь подразумевается, что параметризация опорных кривых совпадает с параметризацией поверхности. На практике такого, как правило, не наблюдается, поэтому выполнение данного условия достигается за счет репараметризации исходных кривых. Исходя из свойств функции Эрмита, видно, что помимо геометрического прохождения через опорные кривые формы Эрмита также задают на границах «потоки» трансверсального вектора (Vu для v-границ и Uv для u-границ).

Для того, чтобы Эрмитовы формы первого направления не вносили вклада в результат вычисления на границах для второго направления, в форму Кунса вводится третье слагаемое, которое для кубической формы записывается следующим образом

$M(u,v)=\{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)} \end{array}\}⋅M_0⋅ \begin{bmatrix} α_1 (v)\\α_2 (v)\\β_1 (v)\\β_2 (v)\end{bmatrix}=\underline{H}(u)⋅M_0⋅\bar{H}(v)(3.1)$

где

${M_0} = \left[ {\begin{array}{*{20}{c}} {r({u_{\min }},{v_{\min }})}&{r({u_{\min }},{v_{\max }})}&{{r_v}({u_{\min }},{v_{\min }})}&{{r_v}({u_{\min }},{v_{\max }})}\\ {r({u_{\max }},{v_{\min }})}&{r({u_{\max }},{v_{\max }})}&{{r_v}({u_{\max }},{v_{\min }})}&{{r_v}({u_{\max }},{v_{\max }})}\\ {{r_u}({u_{\min }},{v_{\min }})}&{{r_u}({u_{\min }},{v_{\max }})}&{{r_{uv}}({u_{\min }},{v_{\min }})}&{{r_{uv}}({u_{\min }},{v_{\max }})}\\ {{r_u}({u_{\max }},{v_{\min }})}&{{r_u}({u_{\max }},{v_{\max }})}&{{r_{uv}}({u_{\max }},{v_{\min }})}&{{r_{uv}}({u_{\max }},{v_{\max }})} \end{array}} \right] (3.2)$

или с учетом совпадения поверхности с образующими кривыми на границах патча:

${M_0} = \left[ {\begin{array}{*{20}{c}} {r({u_{\min }},{v_{\min }})}&{r({u_{\min }},{v_{\max }})}&{{{\dot V}_1}({v_{\min }})}&{{{\dot V}_1}({v_{\max }})}\\ {r({u_{\max }},{v_{\min }})}&{r({u_{\max }},{v_{\max }})}&{{{\dot V}_2}({v_{\min }})}&{{{\dot V}_2}({v_{\max }})}\\ {{{\dot U}_1}({u_{\min }})}&{{{\dot U}_2}({u_{\min }})}&{{r_{uv}}({u_{\min }},{v_{\min }})}&{{r_{uv}}({u_{\min }},{v_{\max }})}\\ {{{\dot U}_1}({u_{\max }})}&{{{\dot U}_2}({u_{\max }})}&{{r_{uv}}({u_{\max }},{v_{\min }})}&{{r_{uv}}({u_{\max }},{v_{\max }})} \end{array}} \right](3.3)$

Из структуры матрицы M0 видно, что элементы первых двух строчек и первых двух столбцов точно определяются образующими кривыми, а остальные элементы представляют смешанные производные, которые должны быть тем или иным образом заданы. Они могут быть выбраны как постоянными, так и зависящими от параметров u и v. Это будет зависеть от формы, в которой будут задаваться функции «потока». Детально этот вопрос будет рассмотрен далее. Сейчас же просто отметим свойство смешанных компонент, требуемое для сокращения функции M (u, v) с Эрмитовой формой Hu (u, v) на u-границах и с Эрмитовой формой Hv (u, v) на v-границах. Рассмотрев границу v=vmin, запишем это свойство в следующем виде (подразумевается, что элементы матрицы M0 могут зависеть от параметров u и v)

$\begin{array}{l} M{0_{33}}(u,{v_{\min }}) = \frac{{d{V_{u1}}}}{{dv}}({v_{\min }})\\ M{0_{43}}(u,{v_{\min }}) = \frac{{d{V_{u2}}}}{{dv}}({v_{\min }}) \end{array}(4)$

Непосредственной подстановкой можно убедиться, что оно обеспечивает сохранность трансверсального вектора Uv1 на границе v=vmin. Подобные же условия можно получить и для остальных границ патча. Таким образом, подводя итог, можно сказать, что форма Кунса обладает следующими свойствами на своих границах

$\begin{array}{l} \frac{{r{{(u,{v_{\min }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{H_v}{{(u,{v_{\min }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{U_1}{{(u)}^{(n)}}}}{{{d^{(n)}}u}}\\ \frac{{{r_v}{{(u,{v_{\min }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{H_v}{{(u,{v_{\min }})}^{(n)}}}}{{{d^{(n)}}udv}} = \frac{{{U_{v1}}{{(u)}^{(n)}}}}{{{d^{(n)}}u}} \end{array} для v=v_{min}$ $\begin{array}{l} \frac{{r{{(u,{v_{\max }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{H_v}{{(u,{v_{\max }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{U_2}{{(u)}^{(n)}}}}{{{d^{(n)}}u}}\\ \frac{{{r_v}{{(u,{v_{\max }})}^{(n)}}}}{{{d^{(n)}}u}} = \frac{{{H_v}{{(u,{v_{\max }})}^{(n)}}}}{{{d^{(n)}}udv}} = \frac{{{U_{v2}}{{(u)}^{(n)}}}}{{{d^{(n)}}u}} \end{array} для v=v_{max} (5)$ $\begin{array}{l} \frac{{r{{({u_{\min }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{H_u}{{({u_{\min }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{V_1}{{(v)}^{(n)}}}}{{{d^{(n)}}v}}\\ \frac{{{r_u}{{({u_{\min }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{H_u}{{({u_{\min }},v)}^{(n)}}}}{{du{d^{(n)}}v}} = \frac{{{V_{u1}}{{(v)}^{(n)}}}}{{{d^{(n)}}v}} \end{array} для u=u_{min}$ $\begin{array}{l} \frac{{r{{({u_{\max }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{H_u}{{({u_{\max }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{V_2}{{(v)}^{(n)}}}}{{{d^{(n)}}v}}\\ \frac{{{r_u}{{({u_{\max }},v)}^{(n)}}}}{{{d^{(n)}}v}} = \frac{{{H_u}{{({u_{\max }},v)}^{(n)}}}}{{du{d^{(n)}}v}} = \frac{{{V_{u2}}{{(v)}^{(n)}}}}{{{d^{(n)}}v}} \end{array} для u=u_{max}$

для любого порядка дифференцирования n.

Очевидно, что форма Кунса может строиться на формах Эрмита разной степени, начиная с линейной формы. В этом смысле формы Эрмита могут иметь разный порядок для направлений u и v. На наш взгляд, без необходимости в использовании формы более высокого порядка нет смысла. К примеру, кубическая форма Эрмита по u оправдана, если поверхность содержит несколько клеток в этом направлении или если задано сопряжение по первой производной на какой-либо из v-границ. Если же ни того, ни другого нет, то достаточно использовать линейную форму. Использование же бикубической формы Эрмита по u

${H_u}(u,v) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)}&{{\gamma _1}(u)}&{{\gamma _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {{V_1}(v)}\\ {{V_2}(v)}\\ {{V_{u1}}(v)}\\ {{V_{u2}}(v)}\\ {{V_{uu1}}(v)}\\ {{V_{uu2}}(v)} \end{array}} \right] = \\ = \underline H (u) \cdot \left[ {\begin{array}{*{20}{c}} {{V_1}(v)}\\ {{V_2}(v)}\\ {{V_{u1}}(v)}\\ {{V_{u2}}(v)}\\ {{V_{uu1}}(v)}\\ {{V_{uu2}}(v)} \end{array}} \right] (6)$

оправдано, если требуется обеспечить гладкую (С2) стыковку между патчами по u направлению или сопряжение по второй производной на v-границах.

После краткого обзора поверхности перейдем теперь к методике расчета функций «потока» (рисунок 4). Функция «потока» может быть получена

путем интерполяции сеточных данных по формулам Эрмита между узлами сетки;
путем непосредственного задания для соответствующих опорных кривых.

Рисунок 4. Функции «потока» для патча поверхности

Сразу скажем, что второй вариант пока не пробовался автором статьи. Однако, очевидно, что такой подход обладает рядом преимуществ, хотя технически и более сложен. Так, например, он позволяет сделать закон «потока» более гибким с точки зрения подстраивания под форму поверхности. Под этим подразумевается возможность задания дополнительных значений вектора во внутренних точках интервала помимо узлов сетки. Данные значения можно найти, например, исходя из решения задачи минимизации функционала кривизны для поверхности. Использование же первого интерполяционного подхода может приводить к неожиданной искривленности или ребристости поверхности, особенно при повышении порядков форм Эрмита или при редкой расстановке образующих кривых. Также явное задание функций «потока» убирает проблему задания узловых смешанных производных, поскольку последние в этом случае вычисляются непосредственно через сами функции.

Рассмотрим теперь метод получения функции «потока» методом интерполяции сеточных данных. Данная методика весьма проста. На примере границы v=vmin рассмотрим «поток» вектора первой производной Uv1(u). Исходя из свойств формы Кунса, в начальной и конечной точках границы патча вектор потока равен

$\begin{array}{l} {U_{v1}}({u_{\min }}) = \frac{{d{V_1}({v_{\min }})}}{{dv}}\\ {U_{v1}}({u_{\max }}) = \frac{{d{V_2}({v_{\min }})}}{{dv}} \end{array} (7)$

Порядок интерполяции будет определяться степенью формы Эрмита в направлении u. Если используется линейная форма, то этих данных будет достаточно для составления функции «потока»:

${U_{v1}}(u) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {\frac{{d{V_1}({v_{\min }})}}{{dv}}}\\ {\frac{{d{V_2}({v_{\min }})}}{{dv}}} \end{array}} \right] (8)$

Если же форма кубическая, то необходимо задание дополнительных величин в узлах сетки, которые имеют смысл смешанных производных. В этом случае функция «потока» запишется как

${U_{v1}}(u) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {\frac{{d{V_1}({v_{\min }})}}{{dv}}}\\ {\frac{{d{V_2}({v_{\min }})}}{{dv}}}\\ {{r_{uv}}({u_{\min }},{v_{\min }})}\\ {{r_{uv}}({u_{\max }},{v_{\min }})} \end{array}} \right] (9)$

Использование бикубического закона приводит к введению еще одной смешанной производной:

${U_{v1}}(u) = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)}&{{\gamma _1}(u)}&{{\gamma _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {\frac{{d{V_1}({v_{\min }})}}{{dv}}}\\ {\frac{{d{V_2}({v_{\min }})}}{{dv}}}\\ {{r_{uv}}({u_{\min }},{v_{\min }})}\\ {{r_{uv}}({u_{\max }},{v_{\min }})}\\ {{r_{uuv}}({u_{\min }},{v_{\min }})}\\ {{r_{uuv}}({u_{\max }},{v_{\min }})} \end{array}} \right] (10)$

В том, что дополнительно вводимые величины имеют характер смешанных производных, можно непосредственно убедиться, рассчитав соответствующие производные формы Кунса (1) с использованием равенств (2), (3) и (8–10). Поэтому, зная их геометрический смысл, можно поискать подход к их адекватному определению. Автор данной статьи использует конечно-разностный подход, при котором расчет смешанной производной выполняется по четырехточечному шаблону в некоторой окрестности узла сетки на базе формы Кунса более низкого порядка, для которой не требуется знание данного узлового параметра. Для примера, смешанную производную ruv можно найти через поверхность, составленную из линейных форм. Это будет выглядеть следующим образом:

${r_{uv}}(u,v) = \\ =\frac{{r(u - du,v - dv) + r(u + du,v + dv) - r(u - du,v + dv) - r(u + du,v - dv)}}{{4 \cdot du \cdot dv}} (11)$

Методика получения функции «потока» для второй производной концептуально ничем не отличается от описанной методики для первой производной. Для бикубической формы Эрмита она запишется как

${U_{vv1}}(u) = \\ = \{ \begin{array}{*{20}{c}} {{\alpha _1}(u)}&{{\alpha _2}(u)}&{{\beta _1}(u)}&{{\beta _2}(u)}&{{\gamma _1}(u)}&{{\gamma _2}(u)} \end{array}\} \cdot \left[ {\begin{array}{*{20}{c}} {\frac{{{d^2}{V_1}({v_{\min }})}}{{{d^2}v}}}\\ {\frac{{{d^2}{V_2}({v_{\min }})}}{{{d^2}v}}}\\ {{r_{uvv}}({u_{\min }},{v_{\min }})}\\ {{r_{uvv}}({u_{\max }},{v_{\min }})}\\ {{r_{uuvv}}({u_{\min }},{v_{\min }})}\\ {{r_{uuvv}}({u_{\max }},{v_{\min }})} \end{array}} \right] (12)$

В то же время введение в расчет функций высоких степеней может быть весьма чувствительным к выбору старших смешанных производных, поэтому степени форм Эрмита лучше разделять и использовать максимально низкие допустимые порядки для конкретной поверхности.

Поскольку функция «потока» может использоваться в том числе и для удовлетворения различных граничных условий, этому вопросу следует уделить особое внимание, учитывая, что он является наиболее сложным в математике поверхности по сети кривых. Говоря о граничных условиях, мы имеем в виду, что поверхность по сети кривых может различным образом стыковаться с другой поверхностью через свою граничную кривую. В этом случае очевидно, что такая граница должна иметь представление поверхностной кривой на указанной поверхности.

Рассмотрим касательное сопряжение и сопряжение по кривизне. Сопряжение по нормали нет смысла рассматривать, поскольку оно принципиально не отличается от сопряжения по касательной. На примере той же границы v=vmin рассмотрим вектор потока Uv1(u). Очевидно, что вектор, рассчитанный по формулам (8), (9) или (10), не обязан удовлетворять граничным условиям сопряжения, поэтому здесь требуется более сложный расчет.

Можно выделить два принципиально разных подхода:

Если в первом случае интерполируются глобальные компоненты x, y и z вектора Uv1(u), то во втором — тангенциальные, нормальные и бинормальные компоненты вектора «потока» с последующим переводом их в глобальную систему координат. Здесь следует уточнить, что тангенциальная компонента направлена вдоль границы сопряжения, нормальная — по нормали к поверхности сопряжения, а бинормальная — перпендикулярно границе в касательной плоскости. Очевидно, что такая интерполяция естественным образом сохраняет условия касательности. Более того, она гарантирует сохранение знака бинормальной компоненты вектора «потока», чего нельзя сказать про более непредсказуемую в этом отношении глобальную интерполяцию.

Рассмотрим теперь первый подход более подробно. По сути, условие касательности для него сводится к исключению нормальной компоненты из вектора «потока»:

${U_{v1}} = {\widetilde U_{v1}} - ({\widetilde U_{v1}} \cdot n) \cdot n (13)$

Кроме того, он накладывает ограничения на значения узловых смешанных производных, которые используются в формулах (9–10) для расчета вектора Uv1(u). Из условия (13) следует, что

${U_{v1}} \cdot n = 0$

Данное тождество означает также и тождественность нулю всех производных данного выражения по u

$\frac{{d{U_{v1}}}}{{du}} \cdot n + \frac{{dn}}{{du}} \cdot {U_{v1}} = 0$

Соответственно, нормальная компонента узловой смешанной производной ruv на границе должна удовлетворять равенству

${r_{uv}}{(u,{v_{\min }})_{norm}} = \frac{{d{U_{v1}}}}{{du}} \cdot n = - \frac{{dn}}{{du}} \cdot {U_{v1}} (14)$

Двойное дифференцирование равенства (14) дает ограничение на нормальную составляющую смешанной производной ruuv

${r_{uuv}}{(u,{v_{\min }})_{norm}} = - \frac{{{d^2}n}}{{{d^2}u}} \cdot {U_{v1}} - 2\frac{{d{U_{v1}}}}{{du}} \cdot \frac{{dn}}{{du}} (15)$

Равенства (13–15) задают формулы для расчета функции «потока» первой производной для выполнения условия касания, а также ограничения, накладываемые на смешанные производные в узлах сетки. На рисунке 5 показана модель с применением сопряжения по первой производной на двух границах.

Рисунок 5. Сопряжение по первой производной. Пример Рисунок 5. Сопряжение по первой производной. Пример

Теперь рассмотрим условия сопряжения по кривизне. Такое сопряжение обеспечивается благодаря коррекции вектора «потока» второй производной (12), нормальная составляющая которого должна иметь строго определенное значение:

${U_{vv1}}{(u)_{norm}} = k \cdot n \cdot U_{v1}^2, (16)$

где k — нормальная кривизна поверхности, рассчитанная в направлении вектора Uv1(u). Таким образом, вектор потока второй производной должен быть представлен в виде двух слагаемых, первое из которых исключает нормальную составляющую от интерполированного вектора, а второе задает требуемое значение для этой составляющей:

${U_{vv1}} = {\widetilde U_{vv1}} - ({\widetilde U_{vv1}} \cdot n) \cdot n + k \cdot n \cdot U_{v1}^2 (17)$

Узловые смешанные производные по аналогии со случаем первой производной должны удовлетворять следующим условиям:

$\begin{array}{l} {r_{uvv}}{(u,{v_{\min }})_{norm}} = - \frac{{dn}}{{du}} \cdot {U_{vv1}} + \frac{{d(k \cdot U_{v1}^2)}}{{du}}\\ {r_{uuvv}}{(u,{v_{\min }})_{norm}} = - \frac{{{d^2}n}}{{{d^2}u}} \cdot {U_{vv1}} - 2\frac{{d{U_{vv1}}}}{{du}} \cdot \frac{{dn}}{{du}} + \frac{{{d^2}(k \cdot U_{v1}^2)}}{{{d^2}u}} \end{array} (18)$

На рисунке 6 показан пример модели с использованием сопряжения по кривизне.

Рисунок 6. Сопряжение по второй производной. Пример Рисунок 6. Сопряжение по второй производной. Пример

Второй метод интерполирования, как уже было сказано, применяется к компонентам вектора в локальной системе координат. Иными словами, для нее требуется построить функцию «потока» в локальной системе координат. Для этого (на примере той же самой границы v=vmin) необходимо перевести узловые трансверсальные векторы rv и их производные ruv и ruuv из глобальной в локальную систему координат. По полученным векторам и их производным по аналогии с формулами (8–10) строится функция Эрмита применительно к локальному базису. Перевод трансверсального вектора и его производной выполняется по формуле:

$\begin{array}{l} {r_v}{(u)_{glob}} = {r_v}{(u)_{loc}} \cdot T(u)\\ {r_{uv}}{(u)_{glob}} = {r_{uv}}{(u)_{loc}} \cdot T(u) + {r_v}{(u)_{loc}} \cdot {T_u}(u) \end{array}, (19)$

где

$T(u) = \left[ {\begin{array}{*{20}{c}} {{\tau _x}}&{{\tau _y}}&{{\tau _z}}\\ {{n_x}}&{{n_y}}&{{n_z}}\\ {{b_x}}&{{b_y}}&{{b_z}} \end{array}} \right] -$

матрица трансформации, τ — касательный вектор, n — нормальный вектор, b — бинормаль в точке.

Также возможен и другой подход к построению функций «потока» в рамках этого метода интерполяции, возможно, более практичный в ряде случаев. Он заключается в обратной последовательности построения, когда сперва строится функция «потока» в локальной системе координат на базе значений вектора «потока» в узловых точках, а уже на основе этой функции определяются смешанные производные в узлах сетки в глобальной системе координат путем перевода из локального базиса.

Изучив описанные два метода построения функций «потока», читатель может задаться справедливым вопросом, какой же способ интерполяции лучше использовать. Однако дать однозначный ответ не представляется возможным. Дело в том, что всегда будут модели, для которых один из методов будет давать существенно худшие результаты, чем другой. Казалось бы, можно просто остановить свой выбор на одном из них, однако разумнее сделать шаг вперед и ввести критерий, с помощью которого можно определить, какой из методов предпочтительнее на конкретном участке границы. Для этого можно рассмотреть на границе сопряжения две близко расположенные друг к другу точки (рисунок 7). Векторы «потока», восстановленные в этих двух точках, пересекаются на некотором расстоянии от границы сопряжения, при помощи которого можно оценить тенденцию функции «потока» к самопересечению.

Рисунок 7. К расчету критерия оценки способа интерполяции Рисунок 7. К расчету критерия оценки способа интерполяции

Сокращая расстояние между двумя близкими точками, можно получить представление данного критерия в дифференциальном виде. Пропустив промежуточные выкладки в целях экономии места и времени, перейдем непосредственно к результату:

$L(u) = \frac{{{{({r_v} \cdot b)}^2} \cdot (\tau \cdot {r_u})}}{{(\tau \cdot {r_v})(b \cdot {r_{uv}}) - ({r_v} \cdot b)(\tau \cdot {r_{uv}})}} (20)$

По величине данного критерия можно сказать, какой способ интерполяции будет лучше: лучший метод будет давать наибольшее расстояние «самопересечения» в наихудшей точке.

Описав методики построения функций «потока» для первой и второй производных, имеет смысл вернуться к обозначенной в начале статьи проблеме, связанной с условиями, накладываемыми на смешанные компоненты в матрице М (u, v), а именнос неоднозначностью их определения в узлах сетки. В идеальном случае производные функции «потока» разных направлений должны давать одинаковые производные при дифференцировании:

$\begin{array}{l} \frac{{d{U_v}}}{{du}} = \frac{{d{V_u}}}{{dv}} = {r_{uv}}\\ \frac{{d{U_{vv}}}}{{du}} = \frac{{{d^2}{V_u}}}{{{d^2}v}} = {r_{uvv}}\\ \frac{{{d^2}{U_v}}}{{{d^2}u}} = \frac{{d{V_{uu}}}}{{dv}} = {r_{uuv}}\\ \frac{{{d^2}{U_v}}}{{{d^2}u}} = \frac{{{d^2}{V_u}}}{{{d^2}v}} = {r_{uuvv}} \end{array} (21)$

Однако, если функции «потока» в силу тех или иных причин дают различающиеся производные в узлах сетки, данные равенства не будут выполняться. Это может происходить, например, в следующих случаях:

в угловых точках сходятся две границы сопряжения, для которых рассчитываются различные смешанные производные;
на границе сопряжения из каких-либо соображений выполняется разделение смешанных производных;
функции «потока» задаются явно и ничего друг о друге не знают.

В этих случаях возникает неоднозначность в выборе смешанных компонент матрицы M0(3), если рассматривать их как постоянные величины, не зависящие от параметров u и v. Обойти это ограничение и обеспечить свойство, сформулированное в формуле (4), можно благодаря определенному функциональному представлению элементов матрицы M0. Суть данного представления можно объяснить на примере «нижнего левого» угла (umin, vmin) патча поверхности. Если представить, что нарушено равенство

$\frac{{d{U_{v1}}}}{{du}}({u_{\min }}) = \frac{{d{V_{u1}}}}{{dv}}({v_{\min }})$

в силу какой-либо из причин, перечисленных выше, то свойства формы Кунса все равно можно обеспечить, если найти такую функцию M033(u, v), что

$\begin{array}{l} M{0_{33}}(u,{v_{\min }}) = \frac{{d{V_{u1}}}}{{dv}}({v_{\min }})\\ M{0_{33}}({u_{\min }},v) = \frac{{d{U_{v1}}}}{{du}}({u_{\min }}) \end{array} (22)$

В качестве такой функции можно взять, например, функцию:

$M{0_{33}}(u,v) = \\ = \frac{{u - {u_{\min }}}}{{(u - {u_{\min }}) + (v - {v_{\min }})}}\frac{{d{V_{u1}}}}{{dv}}({v_{\min }}) + \frac{{v - {v_{\min }}}}{{(u - {u_{\min }}) + (v - {v_{\min }})}}\frac{{d{U_{v1}}}}{{du}}({u_{\min }}) (23)$

В этом случае на границах v=vmin и v=vmax форма Кунса будет определяться формой Эрмита Hv (u, v), а на границах u=umin и u=umax — формой Эрмита Hu (u, v). Поскольку теперь матрица M0 является функцией параметров u и v, то расчет производных для третьего слагаемого формы Кунса (3) становится более сложным:

$\begin{array}{l} {M_u}(u,v) = \underline {{H_u}} (u) \cdot M0 \cdot \overline H (v) + \underline H (u) \cdot M{0_u} \cdot \overline H (v)\\ {M_v}(u,v) = {\underline H}(u) \cdot M0 \cdot \overline {{H_v}} (v) + \underline H (u) \cdot M{0_v} \cdot \overline H (v) \end{array} (24)$

В выражении (24) первые слагаемые для принятого вида функции M033(u, v) обеспечивают удовлетворение граничных условий патча, а вторые слагаемые на границах u=umin и v=vmin равны нулю в силу свойств функций Эрмита и их производных, поэтому в сумме значения функции «потока» для первой производной будут сохранены. На рисунке 8 показана модель с касательными сопряжениями на всех четырех границах поверхности.

Рисунок 8. Модель с сопряжениями на всех границах Рисунок 8. Модель с сопряжениями на всех границах

При использовании бикубической формы Эрмита встает вопрос о расчете вторых производных для третьего слагаемого формы Кунса (3):

$\begin{array}{*{20}{l}} {{M_{uu}}(u,v) = {\underline {{H_{uu}}} (u)} \cdot M0 \cdot \bar H(v) + 2\underline {{H_u}} (u) \cdot M{0_u} \cdot \bar H(v) + \underline {{H}}(u) \cdot M{0_{uu}} \cdot \bar H(v)}\\ {{M_{uv}}(u,v) = \underline {{H_u}} (u) \cdot M0 \cdot \overline {{H_v}} (v) + \underline {{H}}(u) \cdot M{0_u} \cdot \overline {{H_v}} (v) + }\\ { + \underline {{H_u}} (u) \cdot M{0_v} \cdot \bar H(v) + \underline {{H}}(u) \cdot M{0_{uv}} \cdot \bar H(v)}\\ {{M_{vv}}(u,v) = \underline {{H}}(u) \cdot M0 \cdot \overline {{H_{vv}}} (v) + 2 \cdot \underline {{H}}(u) \cdot M{0_v} \cdot \overline {{H_v}} (v) +\underline {{H}}(u) \cdot M{0_{vv}} \cdot \bar H(v)} \end{array}$

В выражении (25) видно, что первые слагаемые для принятого вида функции M033(u, v) обеспечивают удовлетворение граничных условий, а часть последующих слагаемых на границах u=umin и v=vmin равны нулю в силу свойств функций Эрмита и их производных. Однако помимо них в выражении (25) остаются также и ненулевые слагаемые. К счастью, их можно исключить, если функцию M033(u, v) выбрать в несколько ином виде, для которого ее частные производные обращаются в нуль на соответствующих границах патча:

$\begin{array}{l} M{0_{33}}(u,v) = \\ = \frac{{{{(u - {u_{\min }})}^2}}}{{{{(u - {u_{\min }})}^2} + {{(v - {v_{\min }})}^2}}}\frac{{d{V_{u1}}}}{{dv}}({v_{\min }}) + \frac{{{{(v - {v_{\min }})}^2}}}{{{{(u - {u_{\min }})}^2} + {{(v - {v_{\min }})}^2}}}\frac{{d{U_{v1}}}}{{du}}({u_{\min }}) \end{array} (26)$

Можно убедиться, что такой вид функции M033(u, v) обеспечивает на границах u=umin и v=vmin равенство нулю частных производных. Поэтому уравнения (26) принимают вид:

$\begin{array}{l} {M_{uu}}(u,v) = \underline {{H_{uu}}} (u) \cdot M0 \cdot \overline H (v)\\ {M_{uv}}(u,v) = \underline {{H_u}} (u) \cdot M0 \cdot \overline {{H_v}} (v)\\ {M_{vv}}(u,v) = \underline H (u) \cdot M0 \cdot \overline {{H_{vv}}} (v) \end{array} (27)$

что обеспечивает сохранность функции «потока» для второй производной на границах патча.

На этом краткий обзор поверхности по сети кривых можно завершить. В данной статье нами были озвучены общие идеи, заложенные в основе математики поверхности. Ряд выкладок и пояснений был нами опущен, исходя из предположения о наличии у читателя некоторой математической базы, а также в надежде на исследовательскую пытливость, которую он сможет самостоятельно проявить при выводе недостающих в обзоре формул.