Понимание Q-learning, проблема «Прогулка по скале»
Это перевод статьи Understanding Q-Learning, the Cliff Walking problem
Lucas Vazquez

В последнем посте мы представили проблему «Прогулка по скале» и остановились на страшном алгоритме, который не имел смысла. На этот раз мы раскроем секреты этого серого ящика и увидим, что это совсем не так страшно.
Резюме
Мы пришли к выводу, что, максимизируя сумму будущих наград, мы также находим самый быстрый путь к цели, поэтому наша цель сейчас — найти способ сделать это!
Введение в Q-Learning
- Начнем с построения таблицы, которая измеряет, насколько хорошо будет выполнить определенное действие в любом состоянии (мы можем измерить это с помощью простого скалярного значения, поэтому чем больше значение, тем лучше действие)
- Эта таблица будет иметь одну строку для каждого состояния и один столбец для каждого действия. В нашем мире сетка имеет 48 (4 по Y на 12 по X) состояний и разрешены 4 действия (вверх, вниз, влево, вправо), поэтому таблица будет 48×4.
- Значения, хранящиеся в этой таблице, называются «Q-values».
- Это оценки суммы будущих наград. Другими словами, они оценивают, сколько еще вознаграждения мы можем получить до конца игры, находясь в состоянии S и выполняя действие A.
- Мы инициализируем таблицу случайными значениями (или некоторой константой, например, всеми нулями).
Оптимальная «Q-table» имеет значения, которые позволяют нам предпринимать лучшие действия в каждом состоянии, давая нам в итоге лучший путь к победе. Проблема решена, ура, Повелители Роботов :).
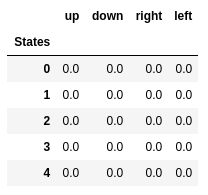
Q-значения первых пяти состояний.
Q-Learning
- Q-learning — это алгоритм, который «изучает» эти значения.
- На каждом шагу мы получаем больше информации о мире.
- Эта информация используется для обновления значений в таблице.
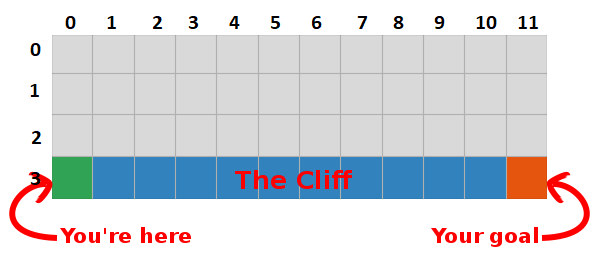
Например, предположим, что мы на расстоянии одного шага от цели (квадрат [2, 11]), и если мы решим пойти вниз, мы получим вознаграждение 0 вместо -1.
Мы можем использовать эту информацию, чтобы обновить значение пары состояние-действие в нашей таблице, и в следующий раз, когда мы посетим ее, мы уже будем знать, что движение вниз дает нам награду 0.
Теперь мы можем распространить эту информацию еще дальше! Поскольку теперь мы знаем путь к цели из квадрата [2, 11], любое действие, которое приводит нас к квадрату [2, 11], также будет хорошим, поэтому мы обновляем Q-значение квадрата, которое приводит нас к [2, 11], чтобы быть ближе к 0.
И это, леди и джентльмены, и есть суть Q-learning!
Обратите внимание, что каждый раз, когда мы достигаем цели, мы увеличиваем нашу «карту» того, как достичь цели на один квадрат, поэтому после достаточного количества итераций у нас будет полная карта, которая покажет нам, как добраться до цели из каждого состояния.
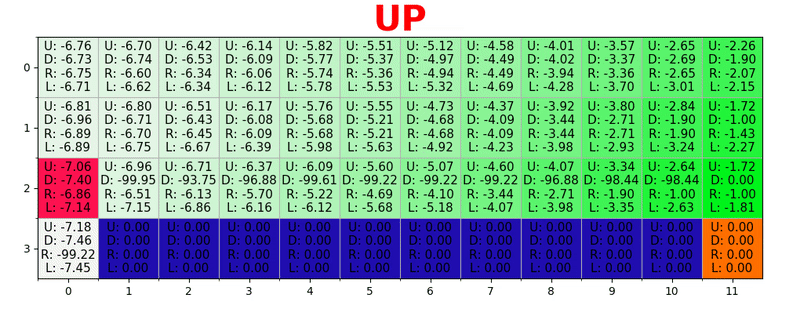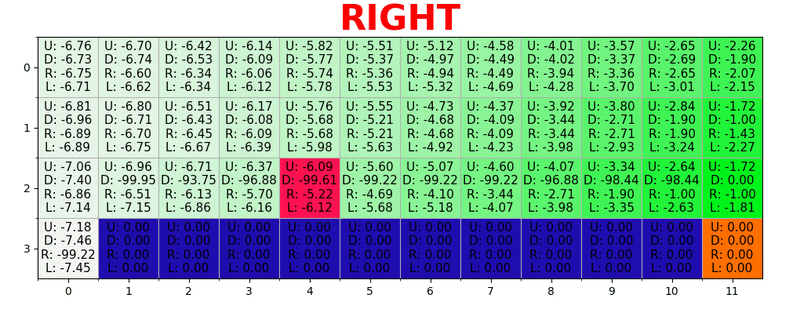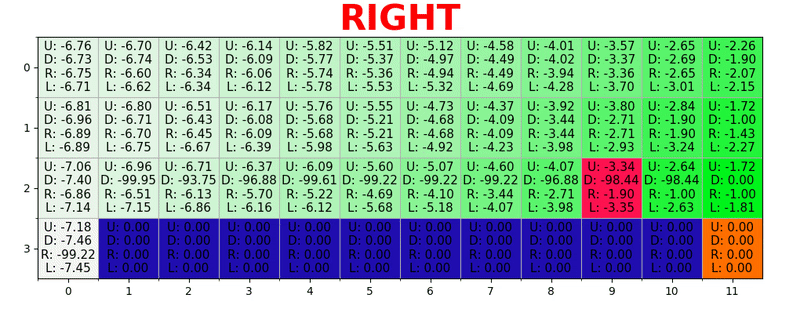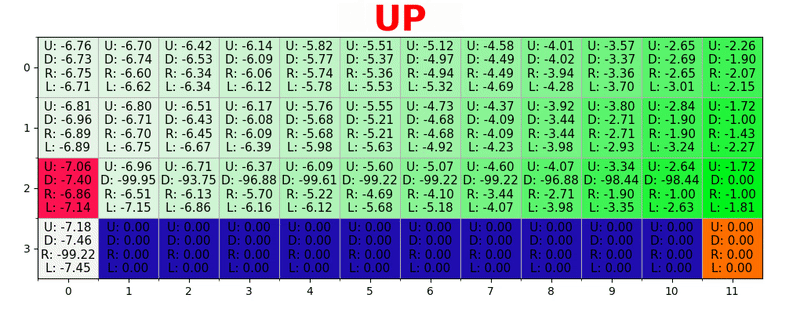
Путь генерируется путем принятия лучших действий в каждом состоянии. Зеленая тональность представляет значение лучшего действия, более насыщенные тональности представляют более высокие значения. Текст представляет значение для каждого действия (вверх, вниз, вправо, влево).
Уравнение Беллмана
Прежде чем говорить о коде, давайте поговорим о математике: основная концепция Q-learning, уравнение Беллмана.

- Сначала давайте забудем γ в этом уравнении
- Уравнение утверждает, что значение Q для определенной пары состояние-действие должно быть наградой, полученной при переходе в новое состояние (путем выполнения этого действия), добавленной к значению наилучшего действия в следующем состоянии.
Другими словами, мы распространяем информацию о значениях действий по одному шагу за раз!
Но мы можем решить, что получение награды прямо сейчас более ценно, чем получение награды в будущем, и поэтому у нас есть γ, число от 0 до 1 (обычно от 0,9 до 0,99), которое умножается на награду в будущем, обесценивая будущие награды.
Итак, учитывая γ = 0,9 и применяя это к некоторым состояниям нашего мира (сетки), мы имеем:

Мы можем сравнить эти значения с приведенными выше в GIF и увидеть, что они одинаковы.
Реализация
Теперь, когда у нас есть интуивное представление о том, как работает Q-learning, мы можем начать думать о реализации всего этого, и мы будем использовать псевдокод Q-learning из книги Саттона в качестве руководства.

Псевдокод из книги Саттона.
Код:
# Initialize Q arbitrarily, in this case a table full of zeros
q_values = np.zeros((num_states, num_actions))
# Iterate over 500 episodes
for _ in range(500):
state = env.reset()
done = False
# While episode is not over
while not done:
# Choose action
action = egreedy_policy(q_values, state, epsilon=0.1)
# Do the action
next_state, reward, done = env.step(action)
# Update q_values
td_target = reward + gamma * np.max(q_values[next_state])
td_error = td_target - q_values[state][action]
q_values[state][action] += learning_rate * td_error
# Update state
state = next_state
- Во-первых, мы говорим: «Для всех состояний и действий инициализируем Q (s, a) произвольно», это означает, что мы можем создать нашу таблицу Q-значений с любыми значениями, которые нам нравятся, они могут быть случайными, они могут быть какими-то постоянными, не имеет значения. Мы видим, что в строке 2 мы создаем таблицу, полную нулей.
Мы также говорим: «Значение Q для конечных состояний равно нулю», мы не можем предпринимать никаких действий в конечных состояниях, поэтому мы считаем значение для всех действий в этом состоянии равным нулю.
- Для каждого эпизода мы должны «инициализировать S», это просто причудливый способ сказать «перезагрузить игру», в нашем случае это означает поставить игрока в исходное положение; в нашем мире есть метод, который делает именно это, и мы вызывая его в строке 6.
- Для каждого временного шага (каждый раз, когда нам нужно действовать) мы должны выбрать действие, полученное из Q.
Помните, я говорил «мы предпринимаем действия, которые имеют наибольшую ценность в каждом состоянии?
Когда мы делаем это, мы используем наши Q-values для создания политики; в этом случае это будет жадная политика, потому что мы всегда предпринимаем действия, которые, по нашему мнению, лучше всего в каждом состоянии, поэтому говорится, что мы действуем жадно.
Барахление
Но с этим подходом есть проблема: представьте, что мы находимся в лабиринте, у которого есть две награды, одна из которых +1, а другая +100 (и каждый раз, когда мы находим одну из них, игра заканчивается). Так как мы всегда предпринимаем действия, которые считаем лучшими, то мы застрянем с первой найденной наградой, всегда возвращаясь к ней, поэтому, если мы сначала узнаем награду +1, то мы упустим большую награду +100.
Решение
Нам нужно убедиться, что мы достаточно изучили наш мир (это удивительно трудная задача). Вот где вступает в игру ε. ε в жадном алгоритме означает, что мы должны действовать жадно, НО делать случайные действия в процентном соотношении ε по времени, таким образом, при бесконечном количестве попыток мы должны исследовать все состояния.
Действие выбирается в соответствии с этой стратегией в строке 12, с epsilon = 0.1, что означает, что мы занимаемся исследованиями мира 10% времени. Реализация политики осуществляется следующим образом:
def egreedy_policy(q_values, state, epsilon=0.1):
# Get a random number from a uniform distribution between 0 and 1,
# if the number is lower than epsilon choose a random action
if np.random.random() < epsilon:
return np.random.choice(4)
# Else choose the action with the highest value
else:
return np.argmax(q_values[state])
В строке 14 в первом листинге мы вызываем метод step для выполнения действия, мир возвращает нам следующее состояние, награду и информацию об окончании игры.
Вернемся к математике:
У нас есть длинное уравнение, давайте подумаем о нем:
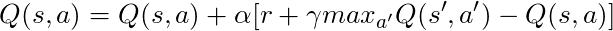
Если мы примем α = 1:
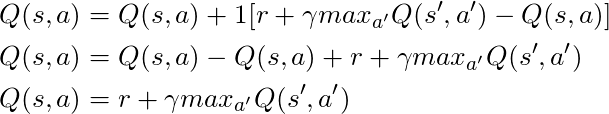
Что в точности совпадает с уравнением Беллмана, которое мы видели несколько абзацев назад! Так что мы уже сейчас знаем, что это строка, ответственная за распространение информации о значениях состояний.
Но обычно α (в основном известная как скорость обучения) намного меньше 1, его основная цель — избежать больших изменений в одном обновлении, поэтому вместо того, чтобы лететь в цель, мы медленно приближаемся к ней. В нашем табличном подходе установка α = 1 не вызывает никаких проблем, но при работе с нейронными сетями (подробнее об этом в следующих статьях) все может легко выйти из-под контроля.
Глядя на код, мы видим, что в строке 16 в первом листинге мы определили td_target, это значение, к которому мы должны приблизиться, но вместо прямого перехода к этому значению в строке 17 мы вычисляем td_error, мы будем использовать это значение в сочетании со скоростью обучения, чтобы медленно двигаться к цели.
Помните, что это уравнение является сущностью Q-Learning.
Теперь нам просто нужно обновить наше состояние, и все готово, это строка 20. Мы повторяем этот процесс, пока не достигнем конца эпизода, умирая в скалах или достигая цели.
Заключение
Теперь мы интуитивно понимаем и знаем, как кодировать Q-Learning (по крайней мере, табличный вариант), обязательно проверьте весь код, использованный для этого поста, доступный на GitHub.
Визуализация испытания процесса обучения:
Обратите внимание, что все действия начинаются со значения, превышающего его окончательное значение, это хитрость для стимулирования исследований мира.
