Понимаем красно-черное дерево. Часть 1. Введение01.05.2021 19:48

Довольно долгое время я воевал с красно-черным деревом (далее — кчд). Вся информация, которую я находил, была в духе «листья и корень дерева всегда черные, ПОТОМУ ЧТО», «топ 5 свойств красно-черного дерева» или »3 случая при балансировке и 12 случаев при удалении ноды». Такой расклад меня не устраивал.

Мне не хотелось заучивать свойства дерева, псевдокод и варианты балансировки, я хотел знать: почему. Каким образом цвета помогают при балансировке? Почему у красной ноды не может быть красного потомка? Почему глубину дерева измеряют «черной высотой»?

Ответы на эти вопросы я получил только тогда, когда мне дали ссылку на лекцию про два-три дерево, с которого мы и начнем.

Эта статья разделена на 3 логические части. Я рекомендую прочитать их в указанном порядке. Первая часть (данная) будет направлена на введение в кчд и знакомство с ним. Во второй части мы поговорим о балансировке и вставке в кчд. В третьей, завершающей, части мы разберем процесс удаления ноды. Наберитесь терпения и приятного чтения:)

Дисклеймер

1. В этой статье не будет информации про плюсы и минусы дерева, его применение и т.д.: информации об асимптотике дерева и работе с ним в интернете полно.

2. Материал предназначен для тех, кто уже знаком с кчд и теперь хочет их понять, а также для тех, кто только знакомится с ними.

3. Статья не будет содержать деталей реализации структуры.

4. Можно считать что эта статья — перевод английского видео материала в упрощенный русский текстовый вариант. Все ссылки я оставляю в конце статьи.

Два-три дерево

Чтобы понять красно-черное дерево, нужно понять два-три дерево

Забегая вперед, скажу, что два-три дерево — это, по сути, родитель нашего кчд, поэтому важно начать именно с него. Поймем два-три дерево — поймем и кчд.

Два-три дерево — абстрактный тип данных, напоминающий по структуре дерево. В нодах два-три дерева может быть одно или два значения и два или три потомка (от чего зависит количество значений и потомков ноды, узнаем ниже). Ноду с одним значением и двумя потомками будем называть 2-нода, ноду с двумя значениями и тремя потомками — 3-нода. Объяснение я начну с создания такого дерева: это наглядно и просто. Но некоторые уточнения нужны все же вначале:

1. Добавляя элемент, мы всегда спускаемся вниз по дереву.

2. Дерево отсортировано классически — меньшие значения находятся слева, бОльшие — справа.

3. Два-три дерево — отсортированное, сбалансированное дерево.

Итак, начнем с первой ноды, это число 5. Тут все просто — 5 становится корнем.

Добавим число 12. Число 12 мы так же добавляем в корень (помним, что нода может иметь два значения), но теперь нам нужно «отсортировать» нашу ноду (сортировать два элемента, ха), т.е. уложить их в порядке возрастания. В итоге получается нода 5–12.

Добавим следующее число. Пусть это будет 17. Давайте пока добавим наш элемент в единственную ноду и снова отсортируем ее. Получилась нода 5–12–17.

Внимательный читатель заметит тут подвох — выше я говорил о том, что наши ноды могут содержать не более двух элементов. Вот тут и происходит магия! Мы берем средний элемент нашей ноды и «просачиваем» его наверх. Итог виден на картинке. Корнем стало число 12, левым сыном число 5, правым — 17.

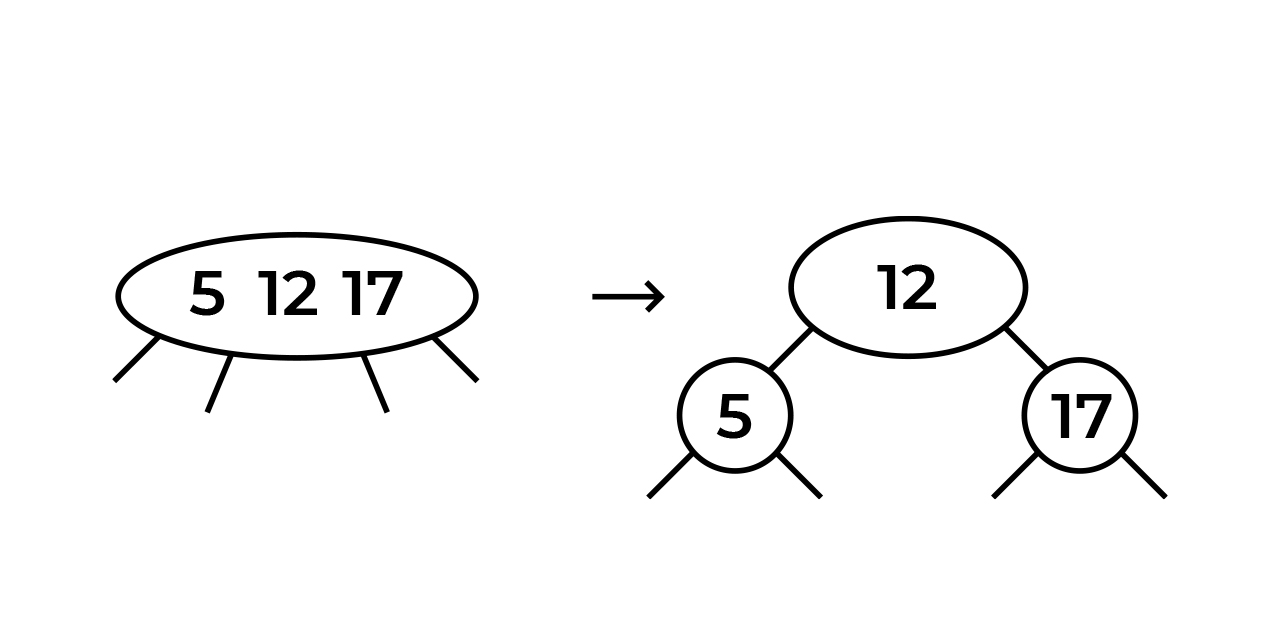
То, что мы сделали выше, можно назвать балансировкой два-три дерева. Правило в этой балансировке простое: если в ноде оказывается три значения, среднее значение мы «просачиваем» вверх. Алгоритм действий зависит от 3 условий:

1. Нода является корнем. Тогда ничего не остается, как создать новую ноду с одним значением и сделать ее новым корнем (как в нашем случае).

2. Родительская нода имеет одно значение. Тогда мы просто добавляем значение к родителю и завершаем балансировку (при этом у родителя появляется третий потомок).

3. Родительская нода имеет два значения. Тогда мы снова просачиваем значение вверх, пока не придем к пункту один или два.

Второй и третий случай балансировки будут рассмотрены ниже.

Окей, идем дальше. Давайте добавим число 3. Так как теперь мы не ограничиваемся одной нодой, спускаемся вниз. Понятно, что спуститься надо влево и добавить 3 к ноде со значением 5. Не забываем расставить 3 и 5 в нужном порядке. В итоге получилась нода 3–5.

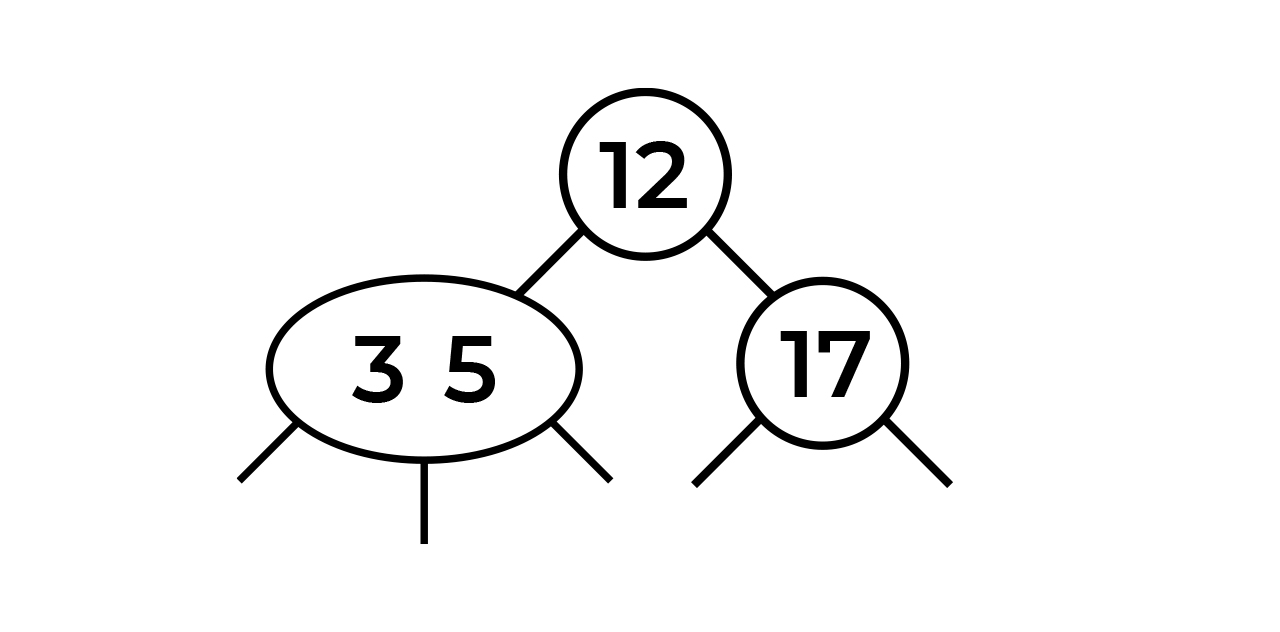
Потерпите, мы близимся к самому интересному:)

Давайте добавим число 4 которое также пойдет влево и присоединится к ноде 3–5. Получится нода 3–4–5, которую, как мы уже знаем, нужно привести к нужному виду. Что делаем? Балансируем наше дерево, т.е. «просачиваем» значение 4 наверх.

Теперь самое интересное. Помимо того, что мы добавим 4 к корню, мы так же добавим корню третьего потомка — это будет нода, которая была больше 4. В нашем случае это 5. Картина будет выглядеть так:

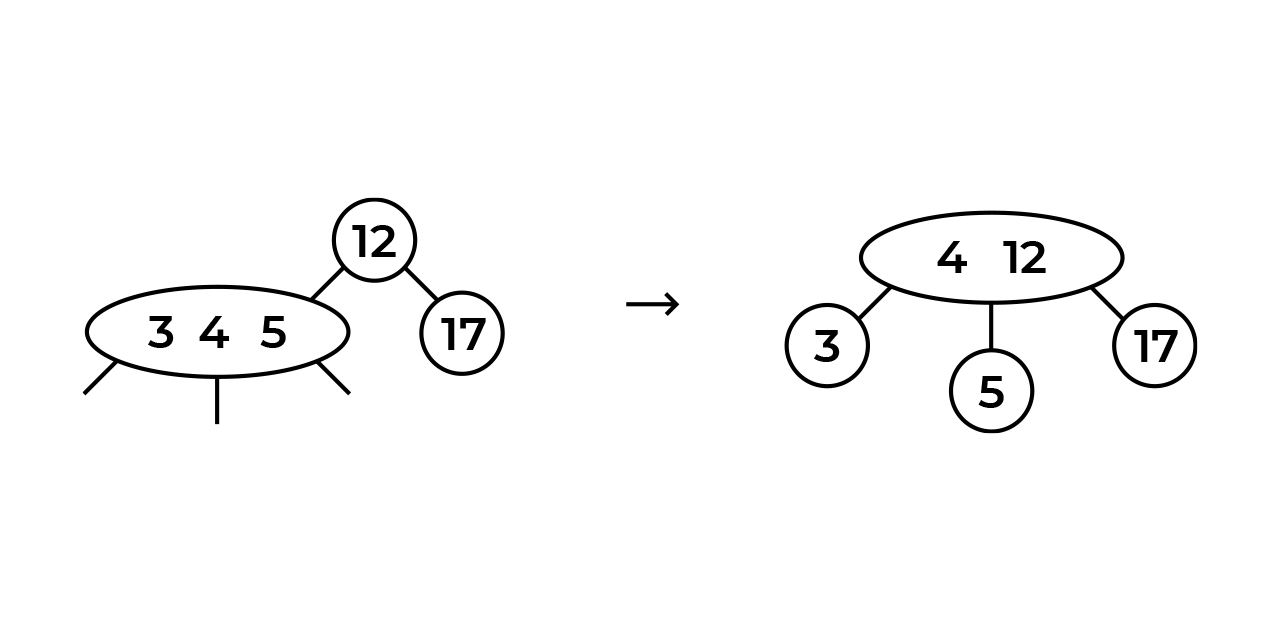
Почему 5 не могла остаться на месте в своей ноде? Тут мы вспоминаем правило отсортированного дерева: значения меньше — слева, значения больше — справа. И так как 5 больше 4, мы не может оставить 5 слева, т.к. это нарушит наш инвариант. Поэтому ноде со значением 5 ничего не остается, как «переехать», и стать потомком ноды 4–12 (кстати, если бы у 5 были потомки, они так же «переехали» бы вместе с родителем).

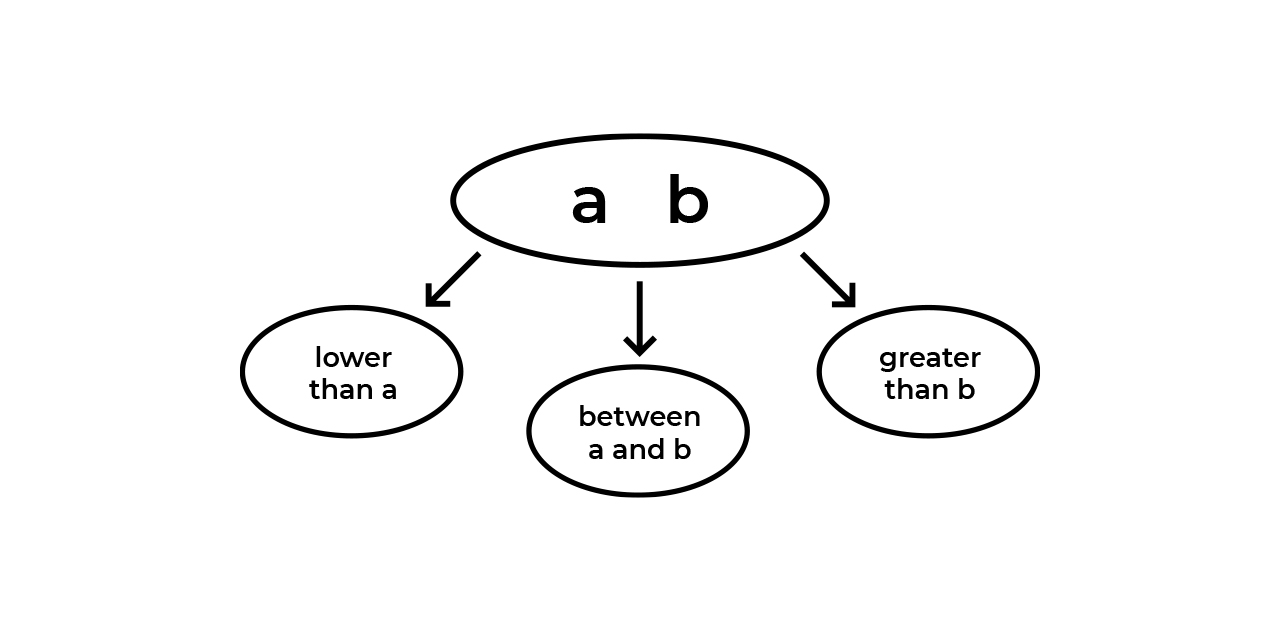
Тут нужно сделать небольшую паузу и объяснить, как ориентироваться в нодах с тремя потомками. Все просто:

1. Значение, что меньше левого значения в ноде, будет левым потомком.

2. Значение, что больше левого, но меньше правого значения в ноде, будет средним потомком.

3. Значение, что больше правого значения в ноде, будет правым потомком.

А теперь посмотрите на то, что получилось. Смело можно заявить, что это отсортированное, сбалансированное два-три дерево. Значения меньше лежат слева, значения больше — справа (тут, как и в случае со значениями 4–5–12, мы считаем, что 5 лежит справа от 4 и слева от 12). Корень имеет два значения и три потомка, что абсолютно соответствует описанию дерева выше. Сейчас вы можете сами попробовать добавить любое значение, чтобы удостовериться, что вы поняли логику (что произойдет с деревом, если добавить значение 7? А затем 9?).

Окей, с самим деревом, я надеюсь, разобрались. Ноды добавляются, дерево балансируется, искать можно, все супер. Но есть нюансы.

Главный минус такой структуры в том, что она, в отличие от бинарного дерева, неудобна в реализации. Нужно следить за количеством потомков и значением, плюс за их порядком, балансировкой (и это я еще не говорил про удаление). Красно-черное дерево решает эту проблему.

Красно-черное дерево

Как мы выяснили, главный недостаток два-три дерева — его структура. Тогда давайте попробуем превратить два-три дерево в дерево бинарное. Как мы можем сделать это?

Чтобы добиться этого, нам нужно простое представление для 3-ноды. Давайте разделим 3-ноду на две 2-ноды и свяжем их ссылками. Пометим эти ссылки каким-нибудь свойством, например, цветом, (возьмём красный), чтобы отличать такие ссылки в дереве от всех остальных.

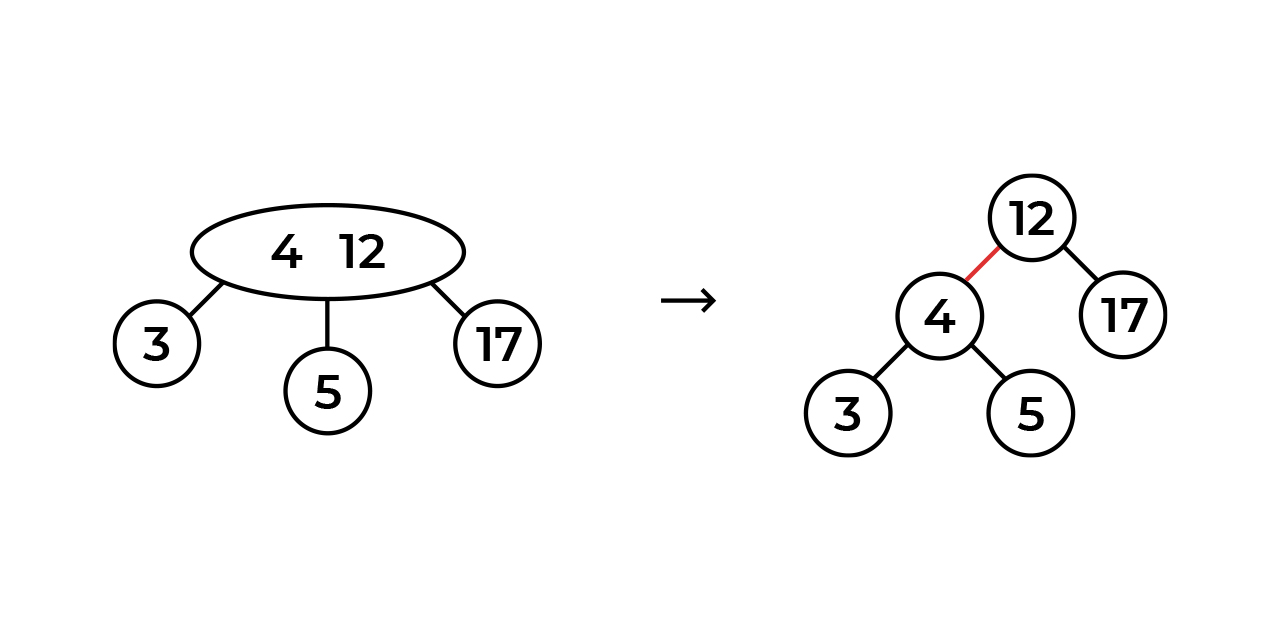
Вообще говоря, мы не можем пометить сами ссылки, поэтому мы помечаем ноды.

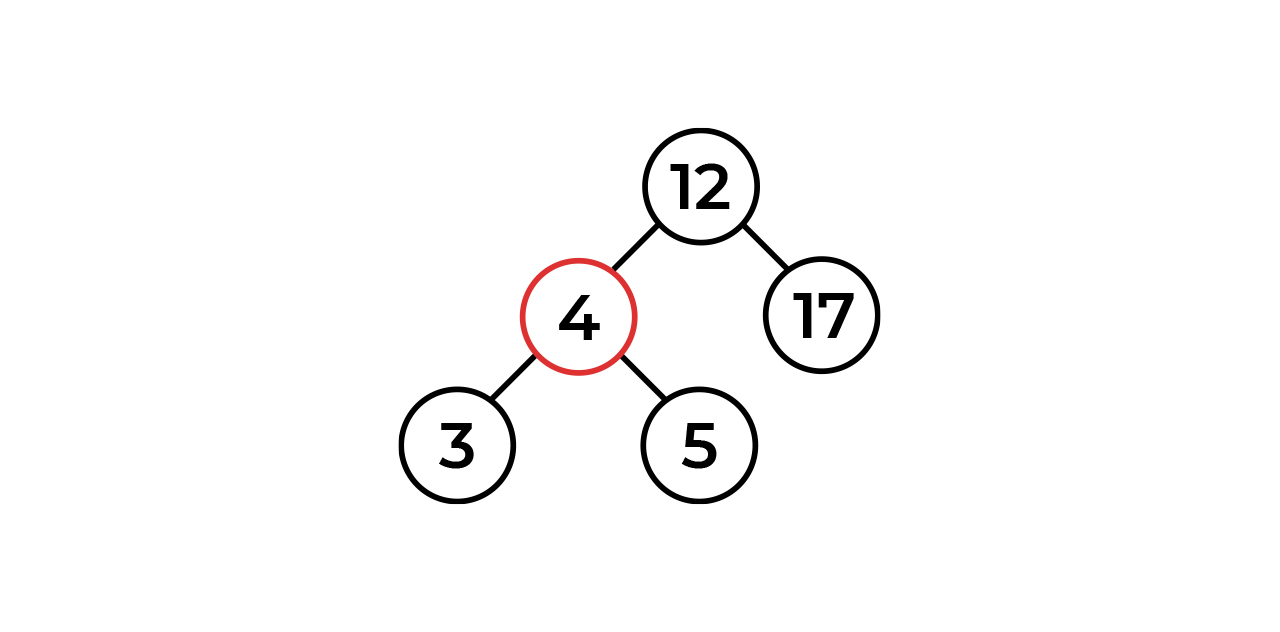
Итак, перед вами красно-черное дерево. Далее, мы разберем несколько свойств кчд, которые я считаю важными (но я думаю, что уже из прочитанного выше многое стало ясно).

Свойства красно-черного дерева

Свойство 1.

Две красные ноды не могут идти подряд. Это свойство приобретает смысл, если мы знаем, что красная нода — это по сути часть 3-ноды в 2–3 дереве. Ну, а если две красные ноды идут подряд, то получается 4-нода, которой у нас не существует:)

Свойство 2.

Корень дерева всегда черный. Опять же, тут все понятно: красная нода не может существовать без потомка.

Свойство 3.

Все null-ноды (ноды, которые не имеют потомков) — черные. Почему именно так, для себя объяснений я не нашел. Но хочу сказать, что это довольно удобное правило, когда дело доходит до балансировки дерева.

Свойство 4.

Высота дерева измеряется только по черным нодам и называется «черной высотой». Тут опять все в целом становится очевидным: красная нода является только дополнением к ноде черной, является ее частью, поэтому высоту принято считать по черным нодам.

На этом введение подходит к концу. В следующей части мы поговорим о том, как вставлять ноды в дерево и балансировать его.