Покоряем высоты для велонавигатора 2ГИС08.06.2022 10:16

26 мая 2ГИС зарелизил велонавигатор. Почитать про него можно тут. Одна из фич велонавигатора — график высот для построенного маршрута. С помощью него:

Эта статья о том, как мы получаем этот график:

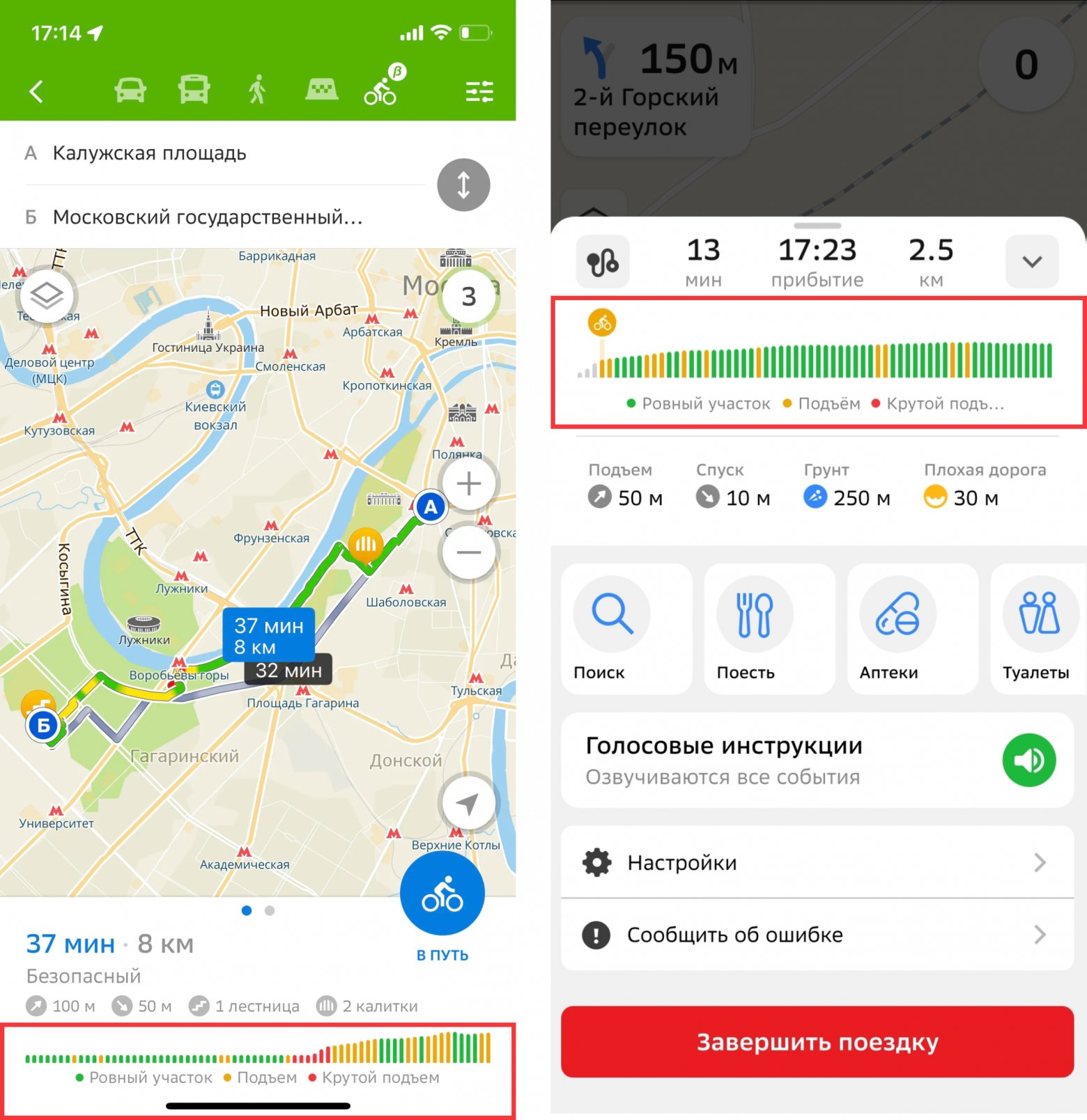
Поехали!

Поймём, в чем задача

Дороги на карте 2ГИС рисуются по дорожному графу. Ребро графа — это участок дороги. Вершины графа — перекрёстки. Посмотрим на примере (место на карте):

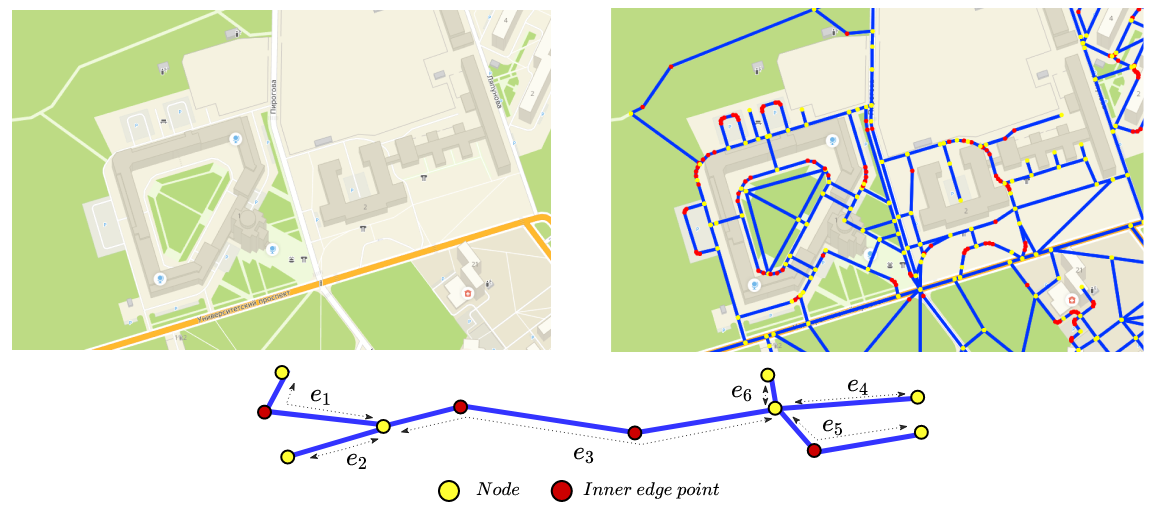
Как видно из примера, геометрия ребра графа — это ломаная. Она хранится в таком виде: LineString (55 44, 55 43, 54 42), где через запятую идут координаты точек ребра (lat, lon). Почитать, что за LineString и что такое WKT можно на вики.

Нам нужно, чтобы геометрия ребра LineString (55 44, 55 43, 54 42) обогатилась высотами, то есть превратилась во что-то такое: LineString (55 44 100, 55 43 200, 54 42 300), где 100, 200, 300 — высоты в соответствующих точках.

Научимся обогащать геометрии ребра высотами — сможем рисовать красивые графики и сделаем пользователей более счастливыми.

Как используем данные GPS для получения высот

Пользователи 2ГИС, используя навигатор, присылают нам свои GPS-координаты. Смартфоны отдают нам обезличенные данные (lat, lon, alt). В будущем по пришедшему запросу (lat, lon) мы хотим возвращать высоту alt.

В одном квадратном метре континуум уникальных точек (lat, lon) (у float«ов конечная точность, но всё равно это очень много уникальных точек!). И не стоит надеяться, что два float«а (lat, lon), которые к нам придут в запросе, будут находиться среди наших наблюдений (lat, lon, alt). Поэтому данные (lat, lon, alt) нужно уметь индексировать по (lat, lon).

Для индексации мы используем пиксельную сетку от Гугла (прочитать про неё и проекцию меркатора можно в доке Google Maps и на вики). Если на пальцах, то мы покрываем карту такой пиксельной сеткой:

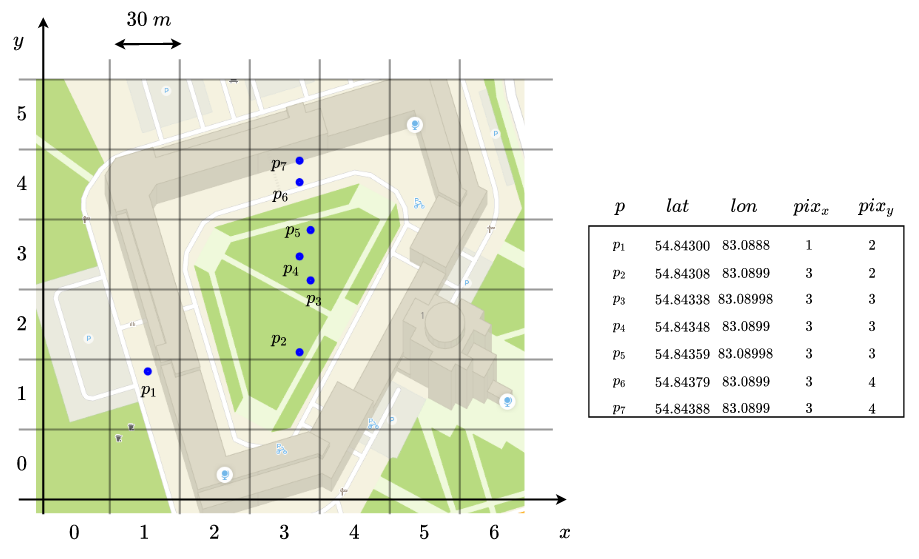
То есть у нас есть отображение

$f: (lat, lon) \longrightarrow (pix_x, pix_y)$

Видно, что точки с разными координатами могут попадать в один и тот же пиксель. Например, точки p_3, p_4, p_5 попали в пиксель (3, 3) .

Размер пикселя — варьируемая величина. В примере выше он около 30 метров.

В будущем мы хотим приписывать пикселю высоту в нём, например, брать среднюю высоту от точек, которые в него попали. Брать пиксель слишком большим — плохо. Если пиксель размером с Новосибирск, то на весь Новосибирск будет одно значение высоты. Слишком маленький пиксель тоже плохо, так как в слишком маленькие пиксели попадает слишком мало точек, данные о высотах получатся слишком шумными и будет много «пустых» пикселей.

У такой координатной сетки есть проблемы. На разных широтах размер пикселя будет разным (см. этот пункт на вики). Например, в Новосибирске размер пикселя может быть 5 метров, а в Москве — 6.

Есть способы индексации, которые устойчивы к этому. Например, от Убера (почему он не подошёл нам, станет ясно чуть позже).

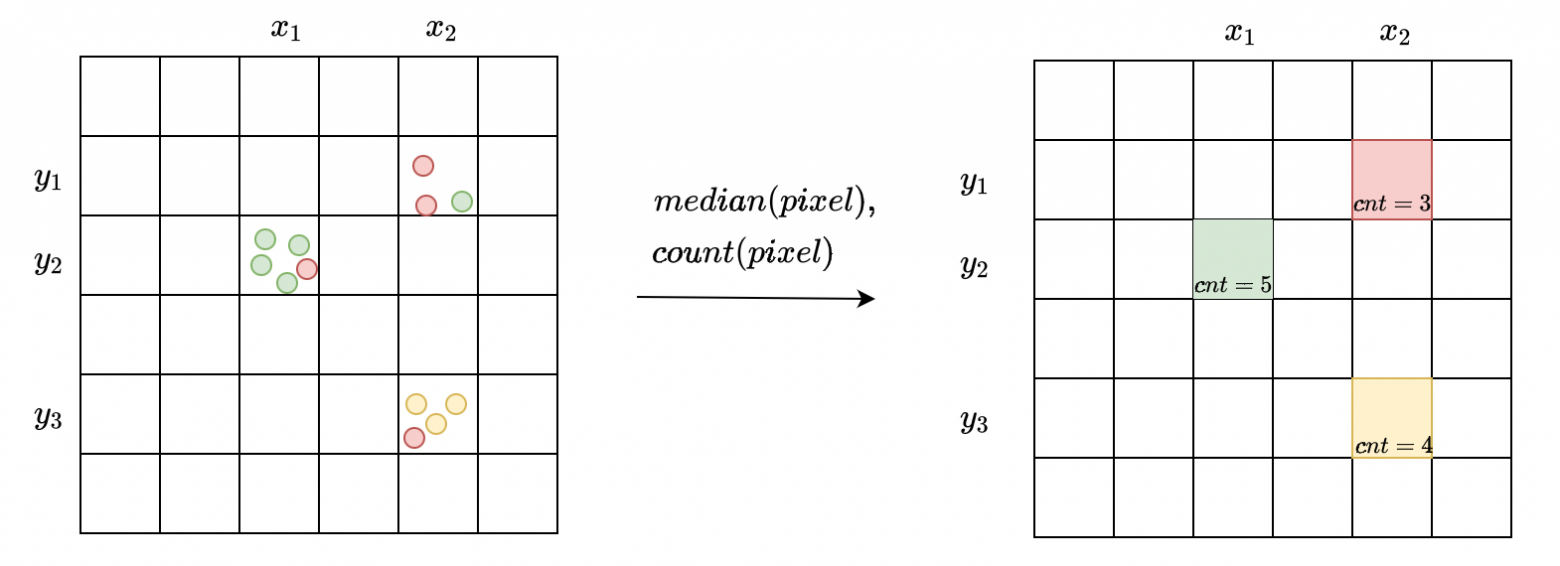
Мы перешли от наблюдений вида (lat, lon, alt) к наблюдениям вида (pix_x, pix_y, alt). Теперь нам нужно присвоить каждому пикселю его высоту. В одном пикселе может находиться много различных наблюдений (lat1, lon1, alt1), (lat2, lon2, alt2), … И это хорошо, потому что GPS штука шумная, и агрегации помогают его потушить. В каждом пикселе возьмем медиану высот от наблюдений, которые туда попали. Запомним также количество наблюдений в каждом пикселе, потом пригодится.

Цвет означает значение высоты: краснее — выше, зеленее — ниже. Берём медиану, а не среднее, чтобы лучше бороться с выбросами.

Ура, мы научились «красить» пиксели! Посмотрим на разукрашенный Владивосток:

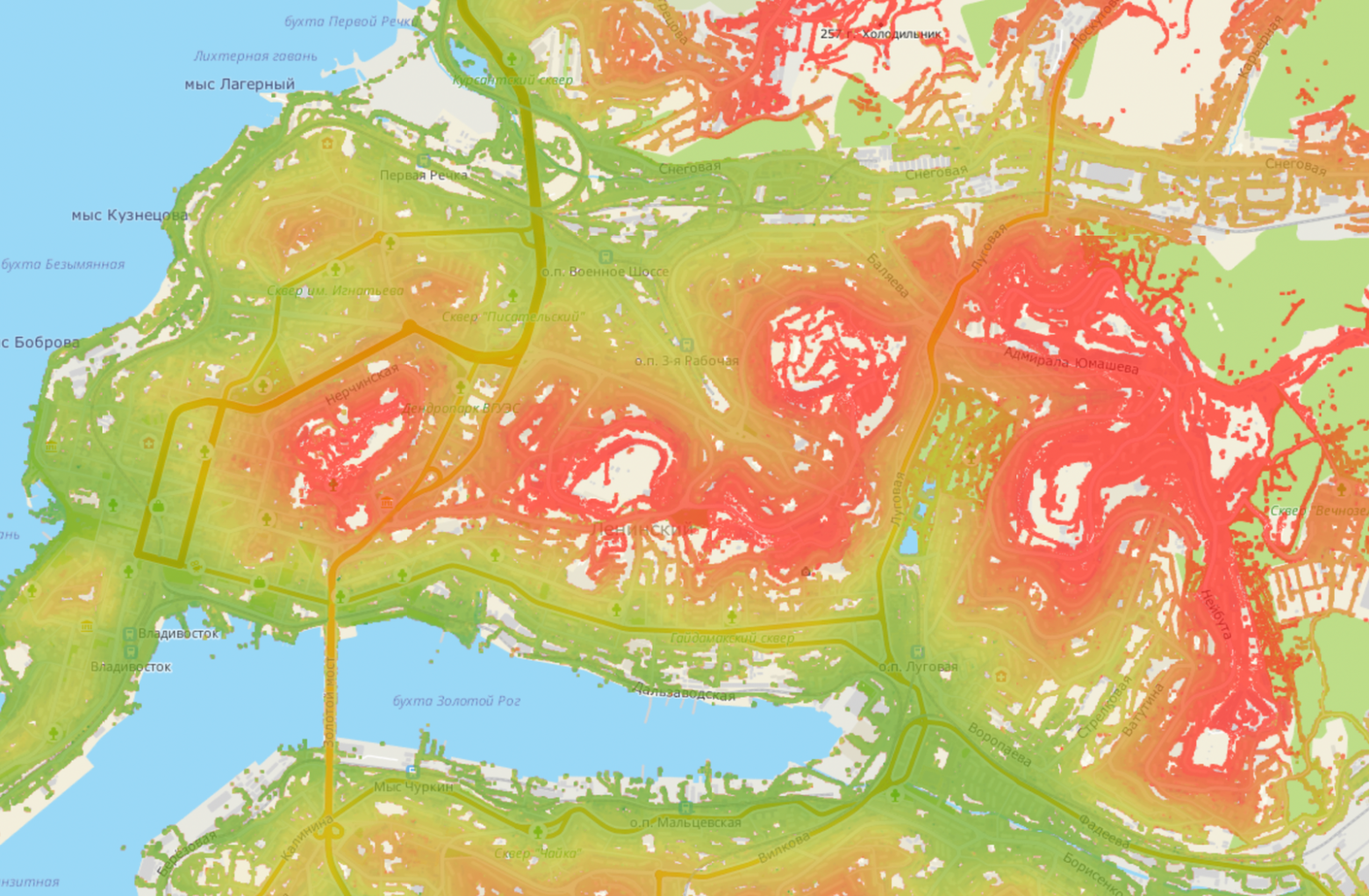
Видно, что мы не красим те места, в которых никто не ездит (например, море:)). То есть сейчас, когда к нам придёт запрос (lat,lon), мы пойдём в соответствующий пиксель и возьмем оттуда значение высоты.

Небольшая мудрость между делом. Когда данных много, можно считать приближённые статистики, чтобы запросы кушали меньше ресурсов. Например, percentille_approx для медианы. Не тратим ману на то, чтобы быть точнее в пятом знаке после запятой :)

Проблемы при раскраске пикселей

Посмотрим на очевидные проблемы, которые могут возникать при раскраске пикселей:

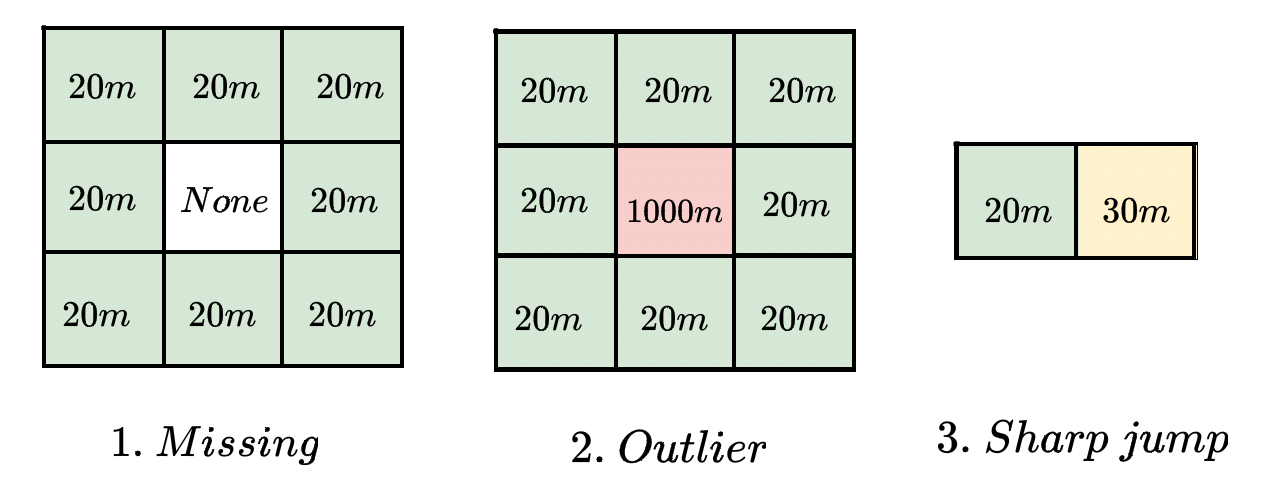
У нас может не быть наблюдений в пикселе, хотя по его окрестности мы можем прикинуть, какая в нем высота.
В пиксель может закрасться выброс, потому что это жизнь : harold:.
Между двумя пикселями резкий переход. Хочется сгладить.

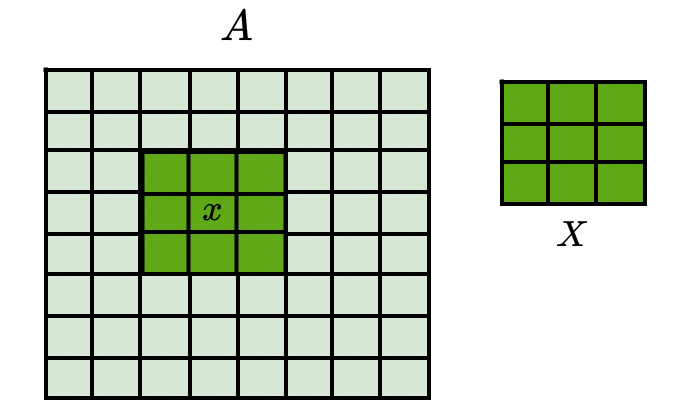
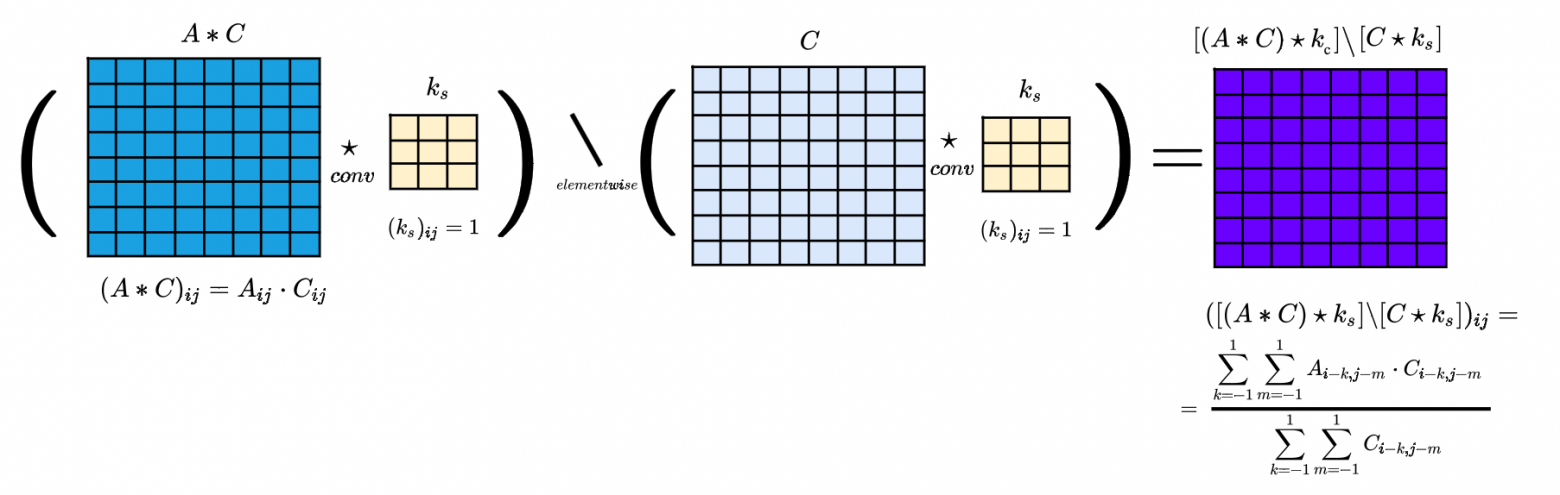
Проблем несколько, решение одно — свёртки! Идея: будем смотреть не только на значение высоты в пикселе, но и на его окрестность. Введем обозначения для матриц и ядер, которые будут использоваться дальше:

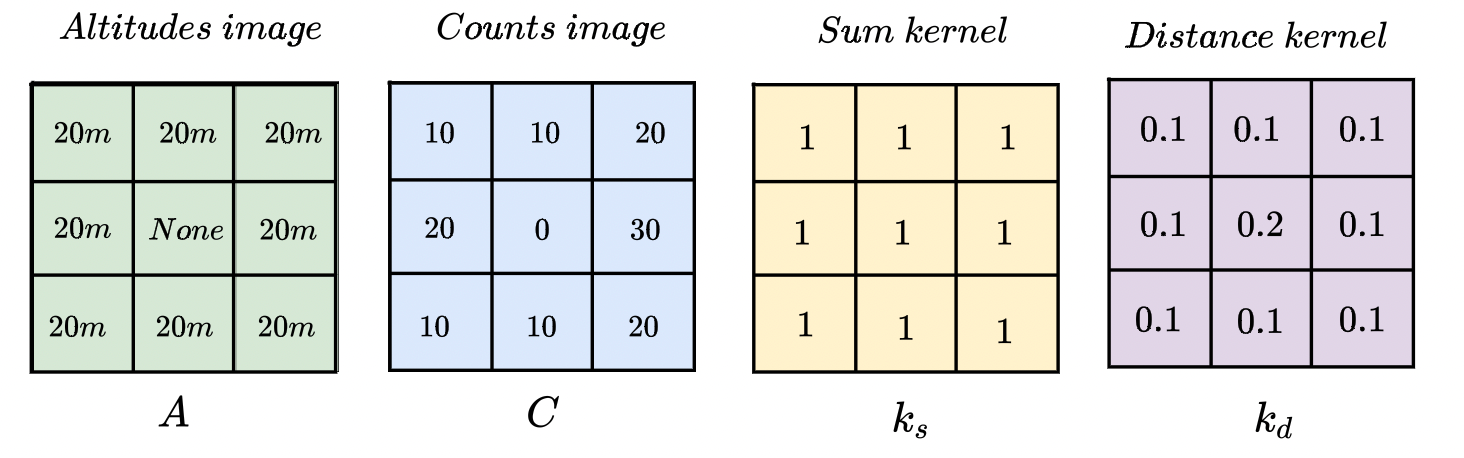
— матрица, в которой элемент — это высота в соответствующем пикселе;
— количество наблюдений, по которым была посчитана высота в данном пикселе;
— ядро, которое мы будем призывать, когда нужно будет где-нибудь получить сумму;
— ядро учёта близости. Когда мы считаем высоту в данном пикселе, мы с бо́льшим весом учитываем значение высоты в нём и с меньшим — значение высоты в окрестности этого пикселя.

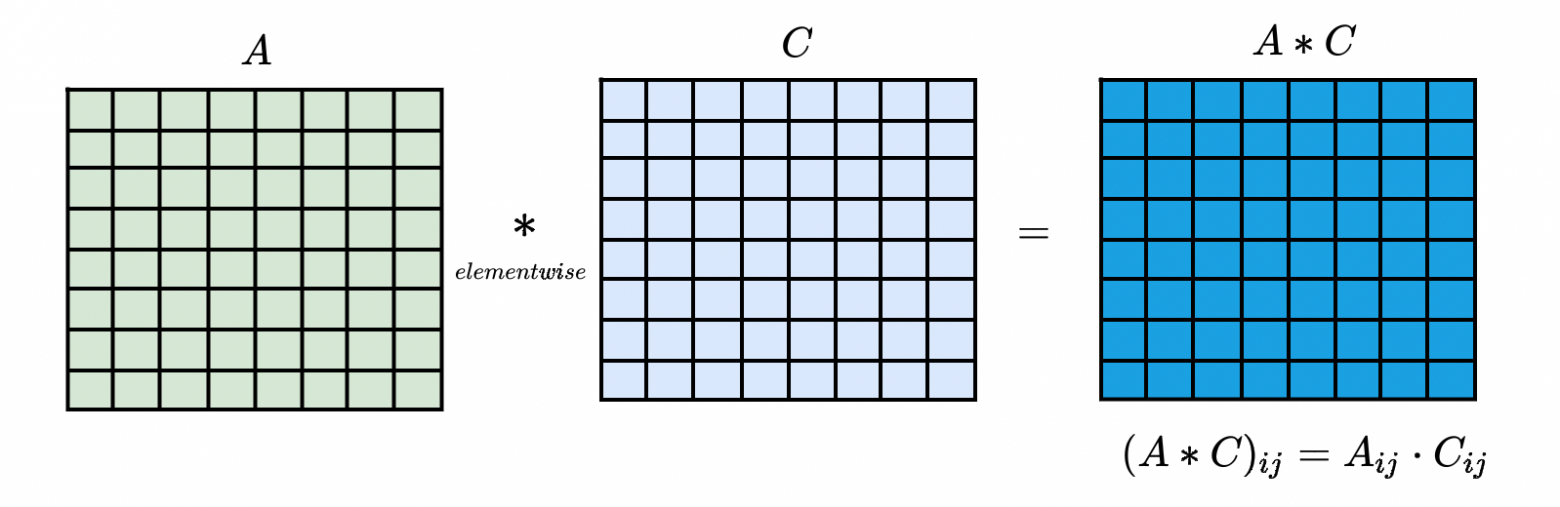
На схеме матрицыи нарисованы как матрицы $3\times 3$ . На самом деле, это большие матрицы (у нас же очень большая «раскрашенная» высотами картинка). Мы используем ядра $5\times 5$ , здесь — $3\times 3$ , чтобы я не умер от рисования.

Если в матрицев пикселе стоит None, то встоит 0. Считаем, что $None\cdot 0 = 0$ .

Решаем проблемы 1 и 3: пропуск и резкий переход

Перед тем, как переходить к формулам, дам немного интуиции.

— высота, — количество наблюдений, по которым считалась медиана.

Пусть мы не знаем высоту в пикселе с вопросиком. Как мы можем восстановить её значение? Можно написать такое выражение:

$a_\color{red}{?}=\sum w_i a_i, \sum w_i=1$

где— значения высот из окрестности неизвестного пикселя. Выражение говорит нам, что мы пытаемся восстановить значение пикселя по соседям с некоторыми весами. Как выбрать веса w_i Будем отталкиваться от двух утверждений:

Высота в пространстве должна изменяться непрерывно.
GPS шумный. И чем больше количество наблюдений мы использовали, чтобы получить значение высоты в пикселе, тем меньше влияние шума.

Поэтому хочется, чтобытем больше, чем он ближе к нашему пикселю и чем по большему количеству наблюдений он был посчитан.

Интуиция дана, теперь покажу, как такое организовать:

В матрице A*C уже не может быть пикселей с так как $None\cdot 0=0$ .

Свернём матрицус ядром:

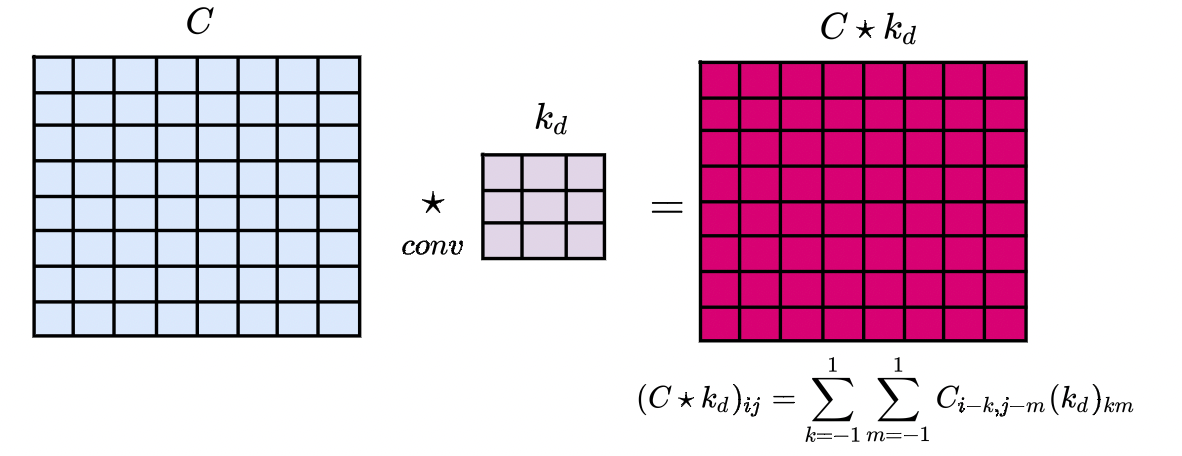
Теперь свернём матрицус ядром:

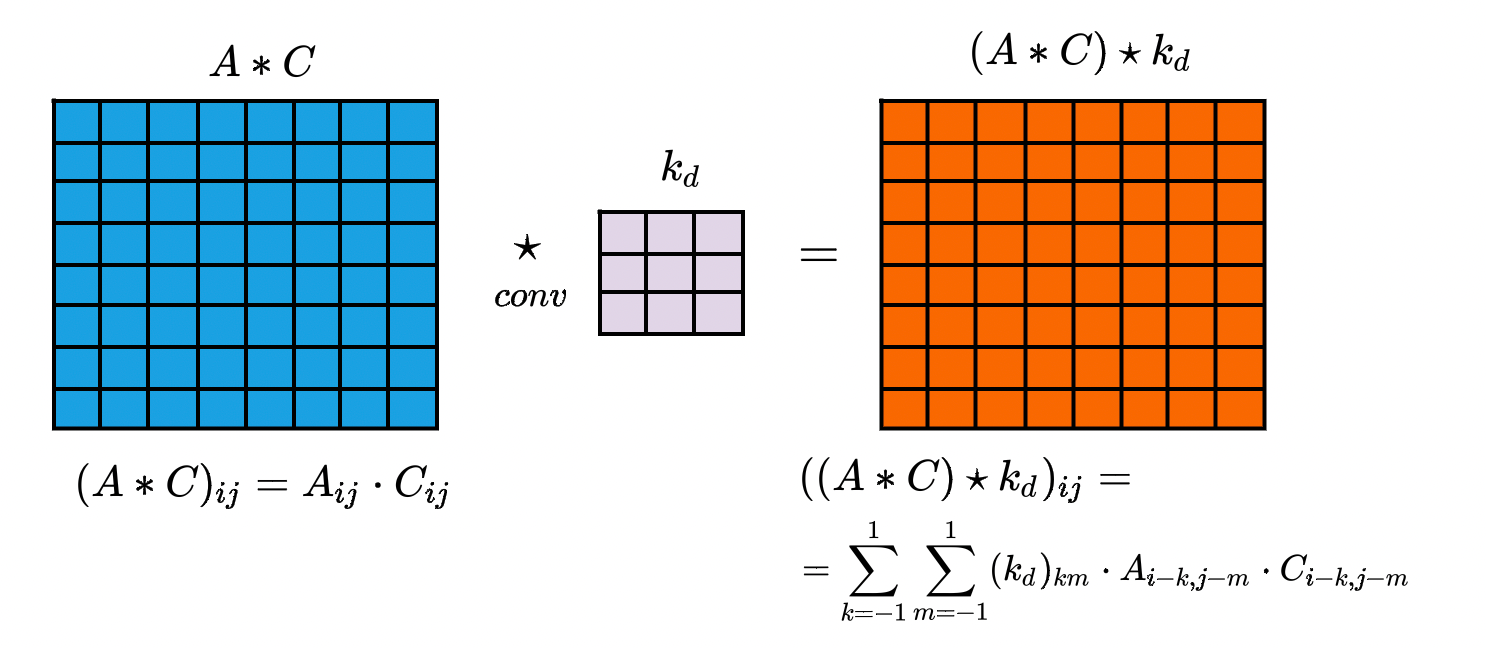
И поэлементно разделим матрицу $(A*C)\star k_d$ на матрицу $C\star k_d$ :

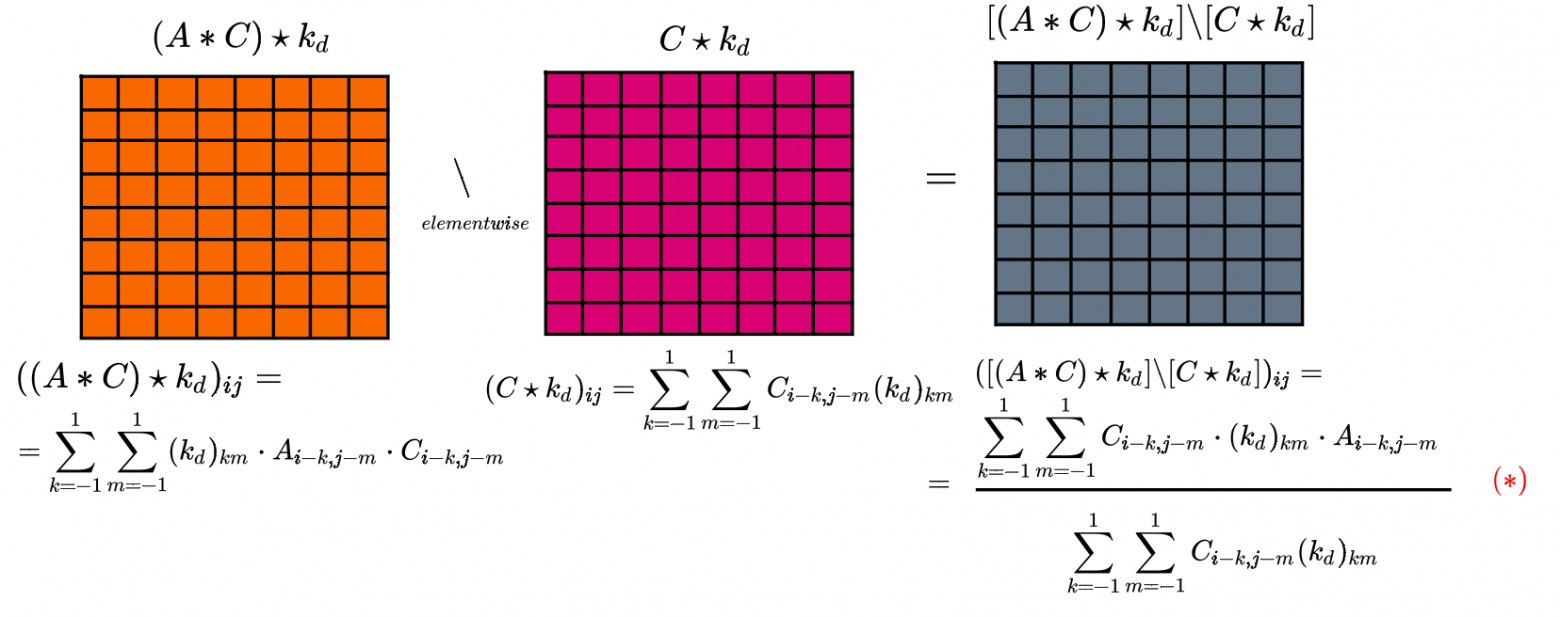
Здесь, что называется, нужно посмотреть на ответ (*) и понять, что он значит. Несколько фактов:

Мартицаимеет размерность метров.
Матрица(количеств) имеет размерность «штуки». Сейчас считаем «штуки» размерными :).
Ядро весовсчитаем безразмерным.

Мы получили размерность $\frac{\text{метры} \cdot \text {штуки}}{\text{штуки}} = \text{метры}$ . Это размерность высот.

Если посмотреть повнимательнее, то значение в пикселе равно взвешенному среднему значению высот в окрестности данного пикселя. Вес тем больше, чем ближе сосед и чем по большему количеству наблюдений в нём получена высота. Звучит как то, что нужно :).

Там, где делим на ноль, выставляем значениевысоты. Деление на ноль означает, что в окрестности пикселя нет ни одного значения высоты $\Rightarrow$ мы ничего не знаем о высоте в пикселе.

Проблема с пропусками решилась — пропуск заполнится, если в окрестности есть пиксели с заполненной высотой.

Проблема с резким переходом частично тоже, так как левый пиксель усреднится (взвешенно) с правым, а правый — с левым (см. последнюю матрицу). Разница высот в таком случае будет меньше, чем исходная.

Взвешивать количеством наблюдений может быть полезно, когда высота в пикселе получена по небольшому количеству наблюдений. Мы больше склонны доверять значениям, которые получены из большего количества наблюдений. Но если в одном пикселе высота была получена по одному миллиону наблюдений, а в другом — по двум миллионам, то лично я буду очень доверять и первому, и второму, так как выборка большая в обоих случаях. А формула выше будет в два раза больше доверять второму. Нехорошо. Самый простой выход — усечь значения матрицыпокакому-нибудь количеству наблюдений, внушающему доверие.

Например, перед всеми вычислениями с матрицами сделать $C_{ij} = max(C_{ij}, 1000)$ . Теперь матрица $[(A*C) \star k_d] \backslash [C\star k_d]$ — это наша матрица с высотами. Обозначим её $A_{final}=[(A*C) \star k_d] \backslash [C\star k_d]$

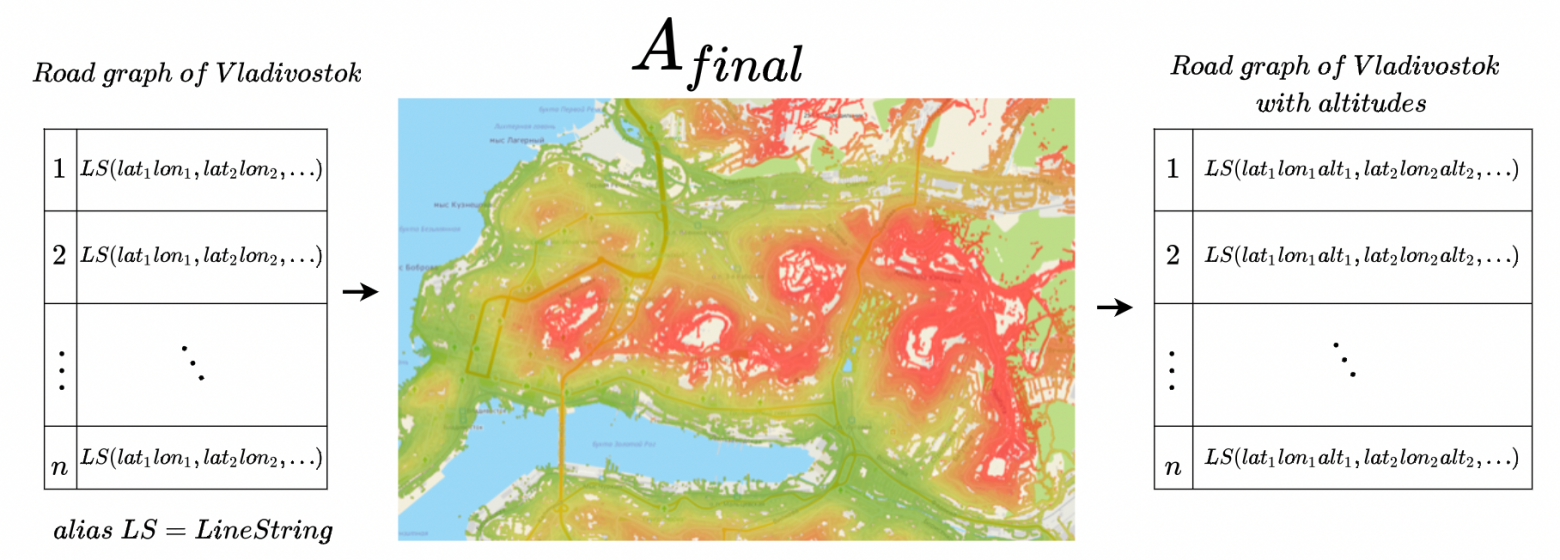
То есть получение высоты для ребра сейчас будет выглядеть так:

Переводим координаты (lat, lon) в (pix_x, pix_y).
Значение высоты в (pix_x, pix_y) спрашиваем в матрице $A_{final}$ .

Разбираемся с проблемой №2: как бороться с выбросами в пикселе

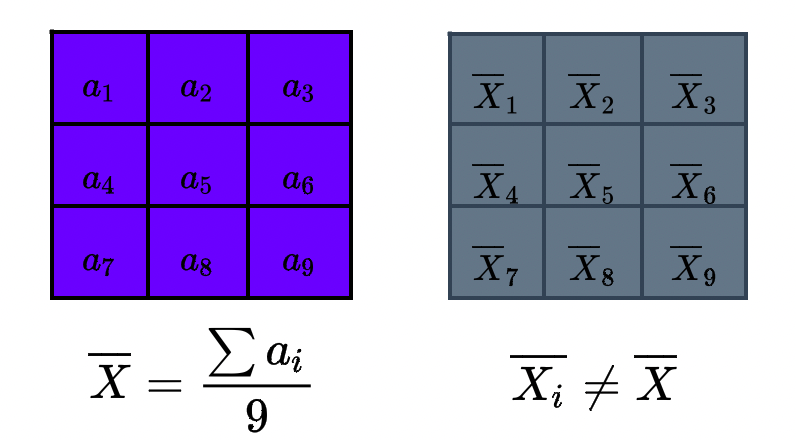
Вспомним, как учат искать выбросы в выборке в школе:

$z_{score} = \frac{x - \overline{X}}{\sigma_X}, |z_{score}| > thr \Rightarrow \ outlier» src=«https://habrastorage.org/getpro/habr/upload_files/6a1/b7f/27a/6a1b7f27a7c8a33f914c8f08f93c77cb.svg» /></p> <p>В наших обозначениях<em><img alt=$ — это значение высоты в пикселе, а выборка— это окрестность этого пикселя.

Лайк, если тоже обожаешь считать статистики по выборкам из 9 элементов :). А вообще, явные выбросы ловятся даже такой небольшой выборкой.

Заметим, что пиксели не входят в выборкуравноправно. Пусть один пиксель был посчитан по миллиону наблюдений, а второй — по десяти наблюдениям. Первый пиксель представляет гораздо большее количество наблюдений, поэтому в принятии решения мы должны опираться больше на значение высоты именно в первом пикселе. В этом нам поможет матрица, в которой записаны количества наблюдений.

Попробуем сообразить выражение для $z_{score}$ через наши матрицы и ядра.

$\overline{X}$ :

Заметим, что в текущей постановке мы пытаемся определить, верим мы пикселю или нет, поэтому свёртки с ядромиспользовать не будем. Опять поумножаем, посворачиваем и поделим:

$[(A\star C) \star k_s] \backslash [C\star k_s]$ — это матрица, где в пикселе написана оценка высоты, посчитанная по его окрестности. В терминах формулы $z_{score} = \frac{x - \overline{X}}{\sigma_X}$ элементы матрицы $[(A\star C) \star k_s] \backslash [C\star k_s]$ — это.

Тогда по формуле среднее = сумма/количество элементов получим матрицу $\overline{X}$ :

$\sigma_X:$

По формуле из школы:

$\sigma_X = \sqrt{(\frac{1}n \sum_i (x_i - \overline{X})^2)}$

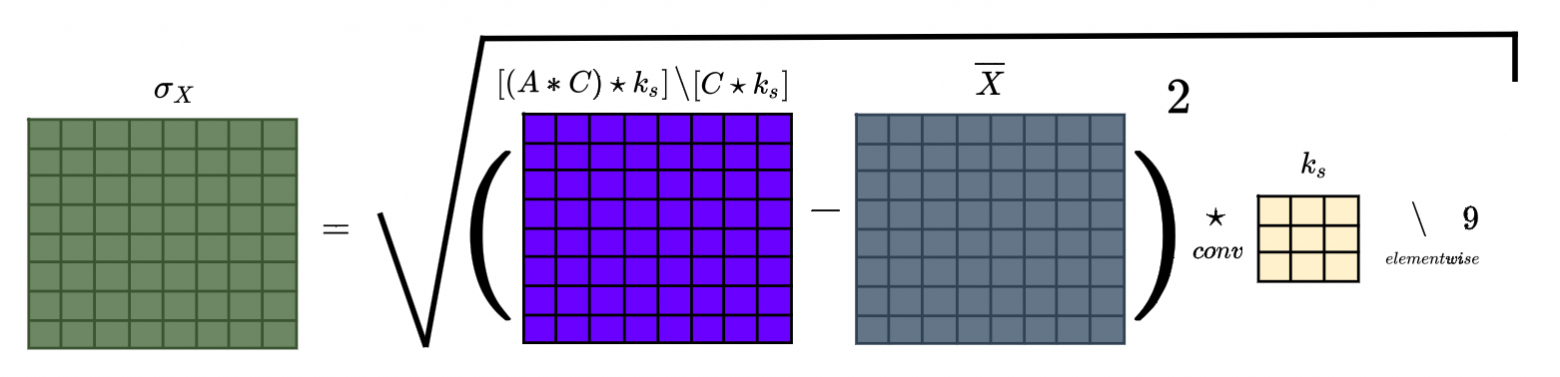
Решение, которое сразу приходит в голову:

из матрицы $[(A\star C) \star k_s] \backslash [C\star k_s]$ вычтем матрицу $\overline{X}$ . Возведём в квадрат, ядром k_s сделаем сумму, потом поделим наи возьмём корень. Мы так и сделаем, но сначала оговорка. В формуле для стандартного отклонения $\overline{X}$ одинаковое для каждого x_i . А в нашем случае каждому x_i соответствует свой $\overline{X_i}$ :

Наш выбор.

Считать формулу для стандартного отклонения по-честному — долго, потому что потому питон. Пока мы обходимся векторными арифметическими операциями и свёртками. Это быстро. Но даже «поломанное» выражение всё равно хорошо детектит выбросы. Тогда $\sigma_{X}$ можем записать как:

Операции возведения в квадрат и взятия корня поэлементные сегодня без жордановых форм. Дальше матрица $z_{score}$ получается из матриц $[(A\star C) \star k_s] \backslash [C\star k_s]$ , $\overline{X}$ , $\sigma_X$ поэлементными вычитаниями и делениями.

Таким образом для каждого пикселя мы научились приближённо считать его $z_{score}$ , а значит, научились отметать выбросы. В пикселе-выбросе полагаем $A_{ij}=None, C_{ij}=0$ .

На всякий случай уточню, что сначала мы убираем выбросы (проблема 2), а затем начинаем лечить проблемы 1 и 3.

Сейчас должно стать понятнее, почему нам не подошел h_3 от Убера. Провернуть подобные трюки гораздо проще и быстрее на прямоугольной сетке (просто работаем с матричками), чем на гексагональной.

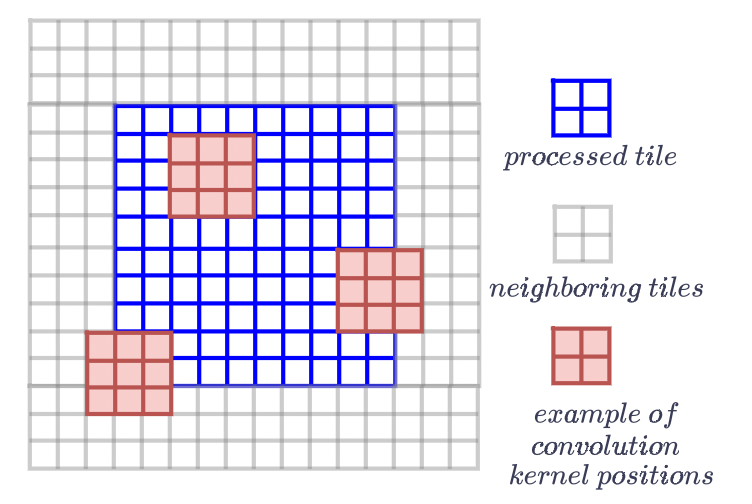
Осталось сказать, что обрабатывать матрицу $A_{final}$ целиком не надо. Все пиксели земного шарика не поместятся в оперативке. $A_{final}$ разбивается на тайлы (подматрицы размера $256\times 256$ пикселей), в которых у нас есть точки GPS — так она и хранится на диске. Все матричные операции выше проделываются над тайлами. Для корректной обработки крайних пикселей при обработке тайла подтягиваются его соседи.

Высотные развязки и тоннели

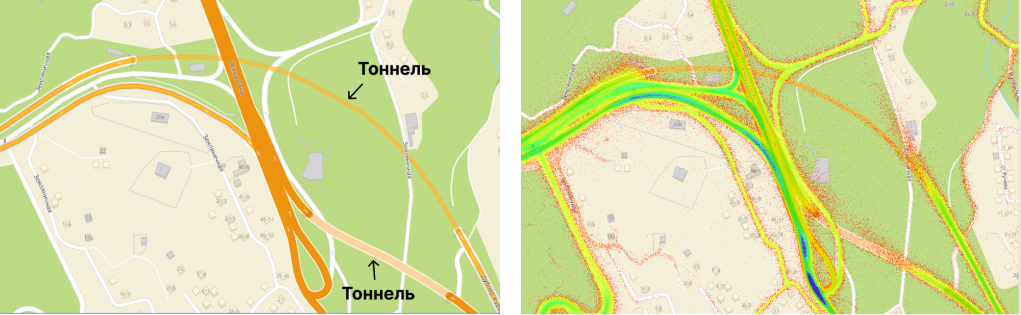
Проблему высотных развязок и тоннелей проще всего показать на конкретном месте:

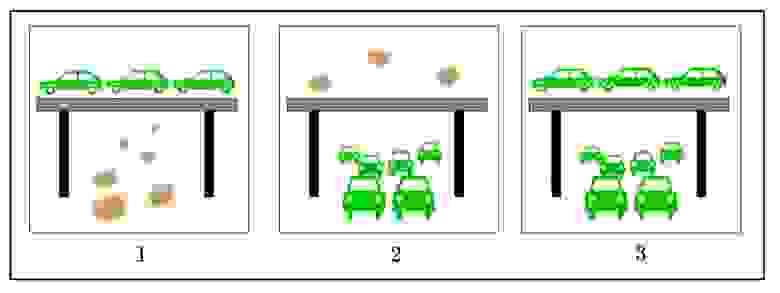
Автомобили, которые едут по мосту и под ним, будут иметь одинаковые координаты (lat, lon). При этом значения высот, которые они будут отдавать, сильно отличаются. Кроме того, под мостом GPS может работать хуже. Тогда возможно несколько неприятных вариантов:

По мосту едет сильно больше машин, чем под мостом.
Для тех, кто на мосту, всё ок. У тех, кто едет под мостом, в графике высот будет резкий подъём, а затем резкий спуск.

Под мостом едет сильно больше машин, чем по мосту
Для тех, кто едет под мостом, всё ок. У тех, кто едет по мосту в графике высот будет резкий спуск, а затем резкий подъем;

Сверху и снизу машин плюс-минус поровну.
И те, и другие не будут рады графику высот, который увидят :)

Посмотрим на карту 2ГИС в каком-нибудь месте с высотной развязкой:

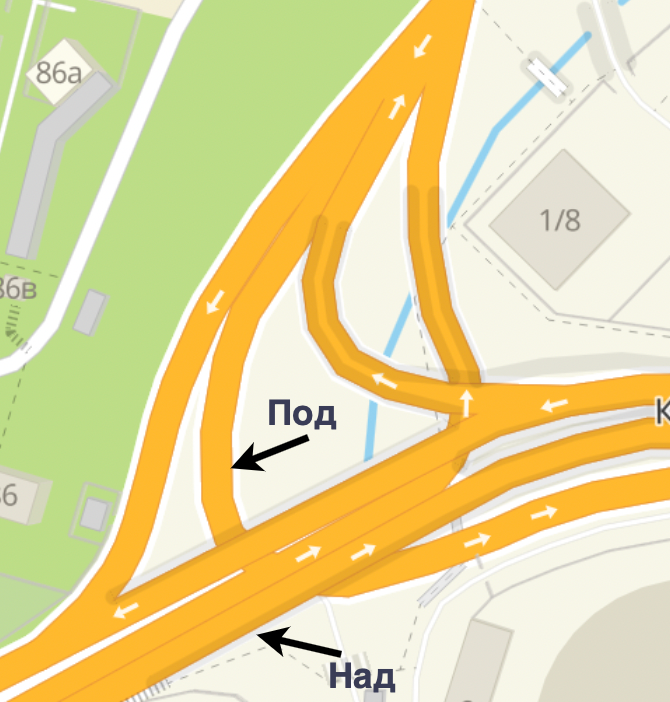
По карте сразу понятно, что одна дорога идет над другой.

Так нарисовать получилось не случайно. Каждое ребро графа содержит целочисленное поле zet_level. Оно помогает нарисовать одну дорогу над другой в случае, когда дороги пересекаются по широте и долготе, но одна дорога проходит над другой. Как раз наш случай.

edge1.zet_level > edge2.zet_level $\Rightarrow$ рисуем edge1 поверх edge2

То есть в наших данных есть информация, что одно ребро находится над другим ребром. Используем её, чтобы решить проблему с высотными развязками.

Алгоритм будет строиться вокруг простого утверждения:

Алгоритм

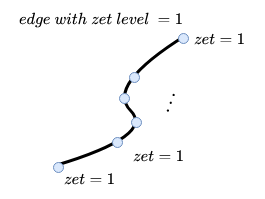
Каждое ребро графа состоит из точек. Присвоим каждой точке графа zet_level, равный zet_level«у её ребра:

Точку ребра назовем плохой, если в её окрестности есть точки с zet level«ами, отличными от zet level«а этой точки. Хорошей — иначе. Пример:

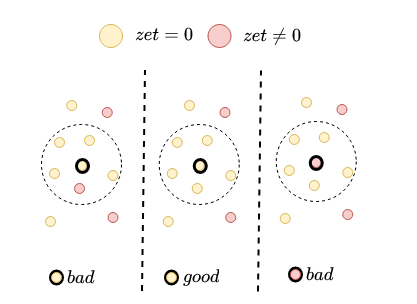
Пример классификации точек на плохие-хорошие для трёх рёбер:

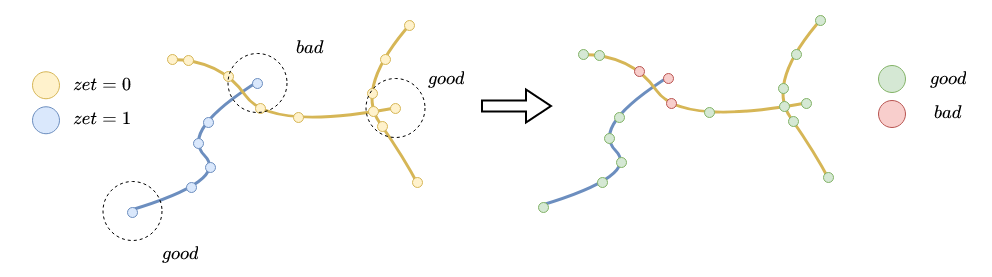
Для хорошей точки мы можем доверять высоте, для плохой — нет. Высоту для плохой точки нужно корректировать. Как корректировать плохую точку p_0 ? Будем аппроксимировать ее высотами хороших точек.

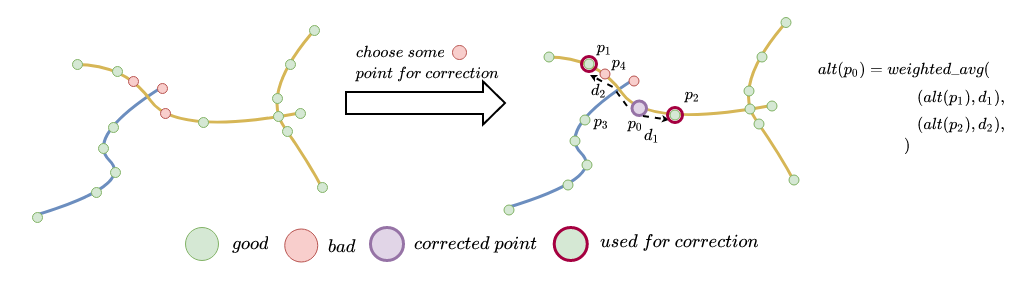
Заметим, что важно брать именно расстояние по графу, а не евклидово расстояние между точками. В примере выше $euler\_dist(p_0, p_3) < euler\_dist(p_0, p_1)$ , но мы не взяли точку p_3 для аппроксимации. Это хорошо, потому что p_3 лежит на более «высоком» ребре, чем точка p_0 . Мы не взяли её, потому что до неё нет короткого пути по графу. А если бы считалось евклидово расстояние, то точка p_3 использовалась бы для корректировки.

Возникает следующая проблема: расстояние между точками на одном ребре может быть большим. В таком случае у предыдущего алгоритма может просто не появиться точек, которыми можно аппроксимировать:

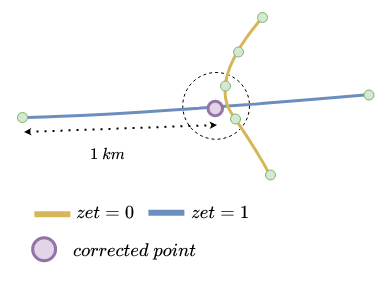
Решим эту проблему введением виртуальных точек на ребре.

Добавим на ребро точки, которые расположены недалеко друг от друга. И применим предыдущий алгоритм к графу, в которых у ребер есть виртуальные точки. Это решит проблему с тем, что нам нечем аппроксимировать плохие точки.

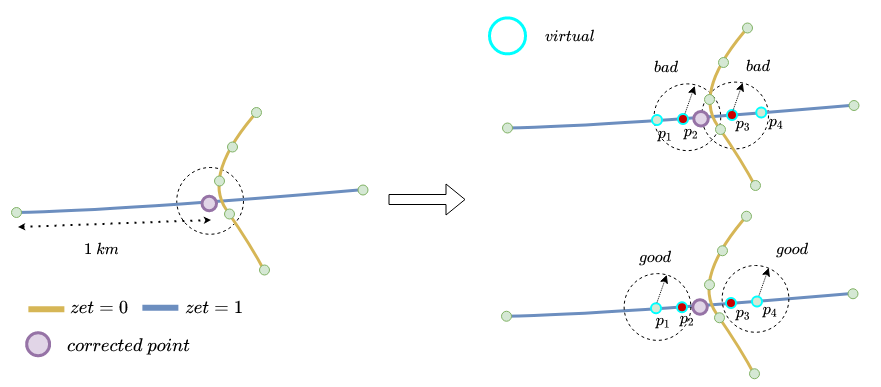
Точки p_2, p_3 плохие, так как в их окрестностях лежат точки с другим zet level (зелёные точки на жёлтом ребре).

Точки p_1, p_4 хорошие, так как в их окрестностях лежат только точки с теми же zet level, что и у них (точки p_1, p_2 ).

Таким алгоритмом лечатся не все высотные развязки. Плохую точку может быть просто нечем аппроксимировать (панорама).

Тут мудрость Конфуция не работает. Пойдём вперед — окажемся под мостом. Назад — тоже. В точках, которые не можем скорректировать, считаем, что не знаем значения высоты. Честно говорим об этом пользователю:

Тоннели

Внутри тоннелей не ловит GPS — это хорошо видно на второй картинке. Тепловая карта точек GPS (чем ярче, тем больше ездили) демонстрирует, что из тоннелей ничего не приходит. А точки GPS, которые попадают на тоннель — это либо шум с соседних дорог, либо загулявшие пешеходы, которые идут над тоннелем.

2ГИС рисует тоннели особым образом (прозрачненько), а значит, у нас есть информация о том, что данное ребро графа — тоннель. В рёбрах-тоннелях заполняем высоты None.

Актуализируем данные высот

Перестроенные рёбера

В дорожном графе 2ГИС могут быть неточности. Например, ребро в графе может быть смещено относительно реальной дороги:

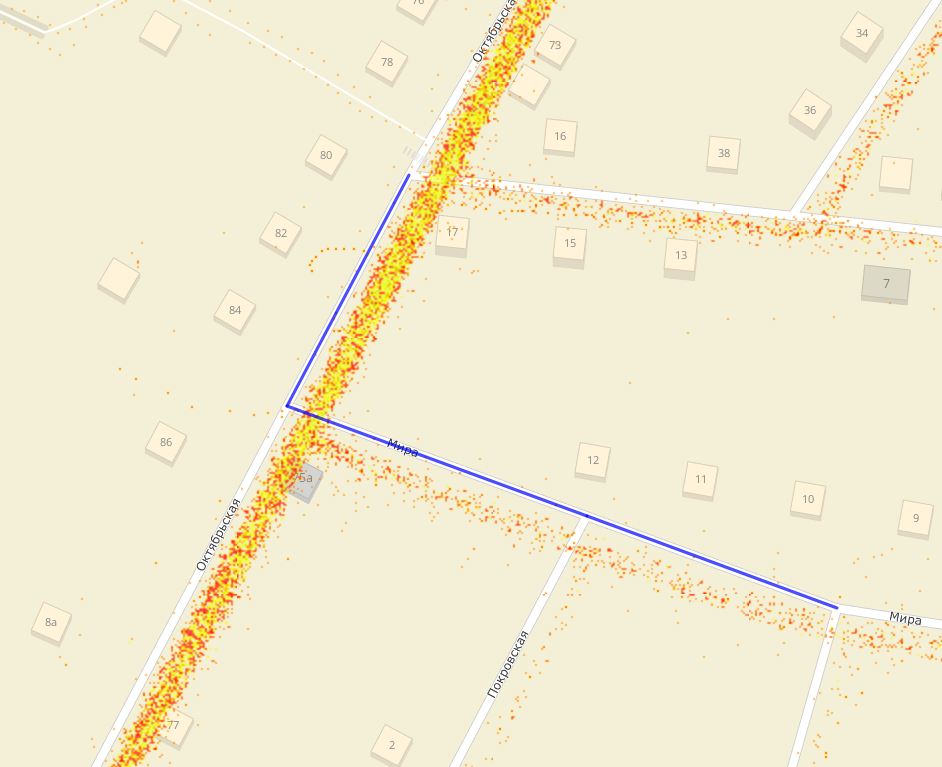
В этом примере красно-жёлтые точки — это то, где ездят люди (GPS), а синим нарисованы ребра, где они должны ездить, согласно нашему графу. Такие расхождения мы исправляем, но ещё не до всех добрались. В этом примере нужно выделенные рёбра подвинуть вправо и вниз.

Так же, например, в графе могут отсутствовать какие-то дороги:

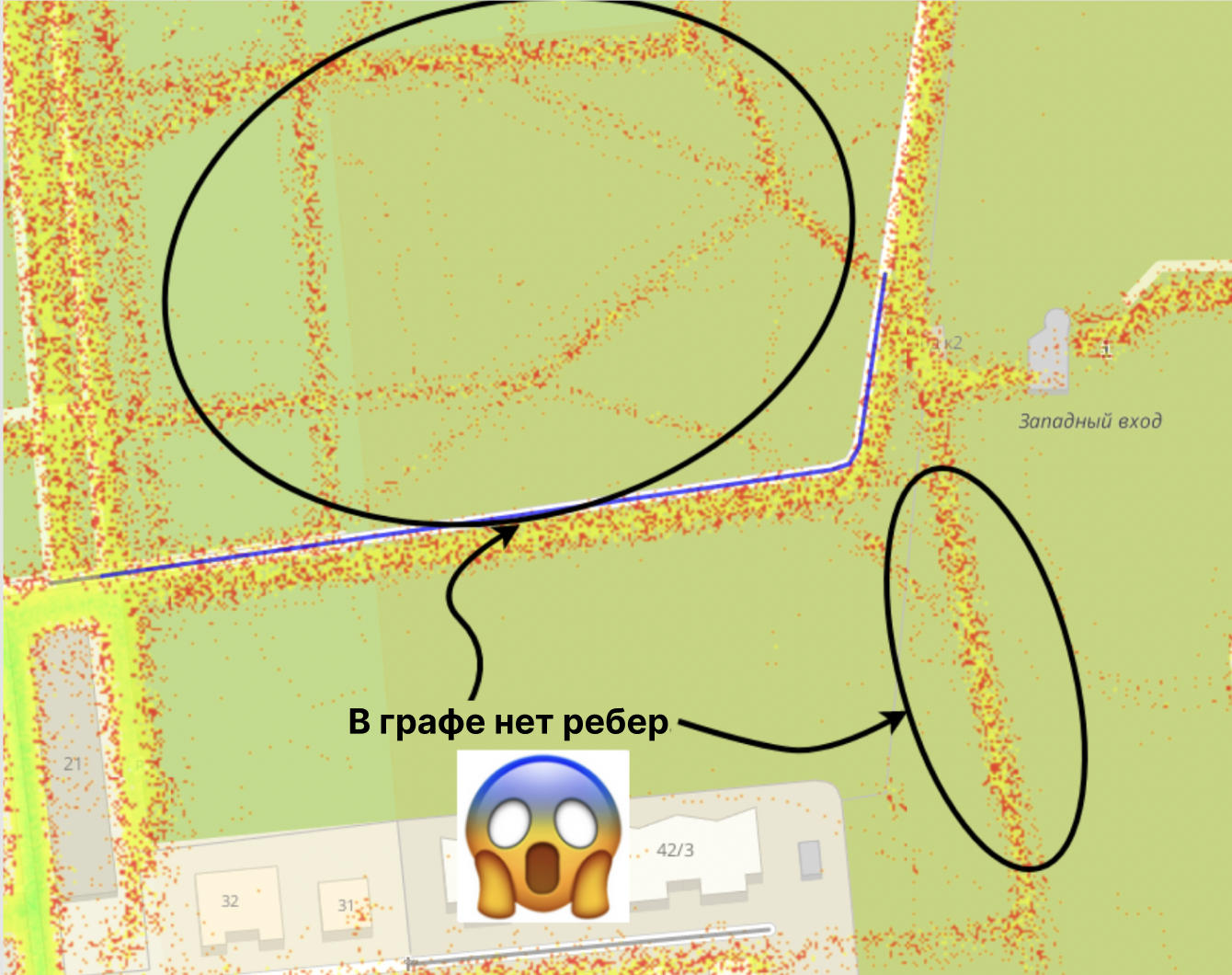
У нас есть внутренние сервисы, которые находят такие места и подсвечивают их картографам. После того, как картограф поправит (или добавит) ребро, у полученного ребра должны обновиться (или появиться) данные о высотах.

Посчитать высоты для нового ребра в отрыве от всего остального графа некорректно: ребро может участвовать в высотной развязке. И если ребро обрабатывается в отрыве от всего графа, то мы это просто не учтём. А для каждого нового ребра пересчитывать весь граф целиком слишком дорого. Воспользуемся тем, что на корректировку высотных развязок для ребра могут влиять только рёбра, которые находятся в некоторой окрестности этого ребра. И сформируем такой запрос к сервису, который обогащает ребра высотами:

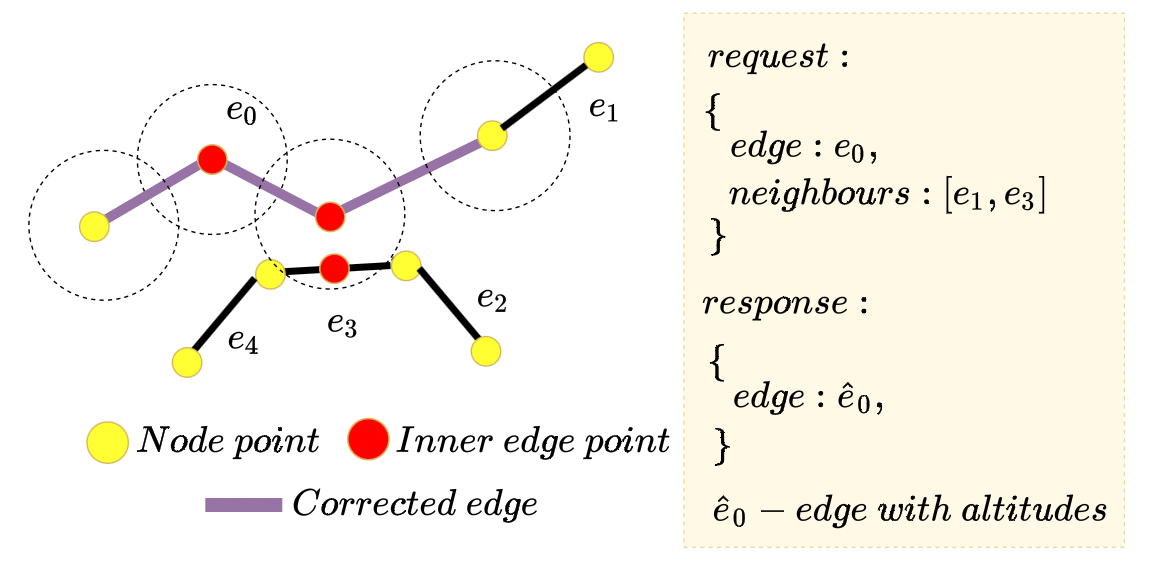
То есть в сервисе, считающем высоты, мы обрабатываем небольшой подграф (ребро с окрестностью) и возвращаем высоты только для нужного ребра.

Актуализация данных высот

Напомню, что данные о высотах хранятся в матрице $A_{final}$ :

Когда автомобили начнут ездить по свежепостроенной дороге, у неё не появится высот, если не обновлять матрицу. Поэтому раз в несколько месяцев будем обновлять $A_{final}$ с учётом новых наблюдений и, соответственно, будем обновлять дорожный граф.

Как понять, что становится лучше

Я рассказал о нескольких алгоритмах. Как понять, что они улучшают ситуацию относительно решения «в лоб»?

Это большая боль в этой задаче. У нас нет возможности получить точные значения высот для всех рёбер в каком-нибудь городе. В терминах машинного обучения это значит, что у нас нет $y_{ground \_ truth}$ для подсчета честных метрик. Будем изворачиваться :)

Есть открытые источники с данными о высотах. Им верить можно не всегда, данные о высотах в них зачастую неактуальны (если построили новую высокую дорогу, в источнике это не отразится). Но есть области на карте, где новые дороги не строились много лет, и мы об этом точно знаем. В таких областях мы можем взять из открытых источников перепады высот в качестве $ground \ truth$ и сравнить с перепадами высот, которые получились у нас.
Также на помощь приходят различные прокси-метрики качества, посчитанные по графу. Приведу пример одной из них. Пусть есть ребро длиной 5 метров, а перепад высот между его крайними точками — 100 метров. В реальности такое ребро просто не может встретиться. А из-за выбросов в GPS — запросто. При работе над алгоритмами очистки выбросов можно считать долю ребер, у которых отношение перепада высот к длине больше некоторого порога, $\frac{|\Delta alt|}{length} > thr» src=«https://habrastorage.org/getpro/habr/upload_files/200/f35/189/200f3518908d2cd71c0a3a4b46481efb.svg» />. Если этот процент уменьшается, это косвенно сигнализирует нам, что новый алгоритм очистки выбросов лучше предыдущего.</p></li><li><p><strong>Корректировка высотных развязок</strong>. Можно самим наковырять пару сотен высотных развязок. Для каждой развязки можно добыть фотографий, чтобы понять, как она выглядит, и на глаз прикинуть, сколько метров между дорогами «над» и «под». Затем посмотреть, что предсказывалось до корректировки и после. И делать выводы о том, насколько корректировка улучшает ситуацию.</p><p>Потянулись, улыбнулись, </p></li></ol> <h2>Рефлексируем</h2> <p>Вот такой фит-предикт получился. Изначально решение задачи для меня выглядело как «да ща бахнем запросик тут, усредним там и все будут довольны, подержи мое пиво». Но в ней оказалось много интересных подводных камней. Здесь описал не все из них и не все костыли методы их обхода. Выбрал только наиболее интересное, чтобы статья не стала слишком большой и у меня не развился туннельный синдром от рисования картинок. </p> <p>Спасибо за внимание! </p> <p>Титры…</p> <h2>Сцена после титров</h2> <h3>Приручаем GPS</h3> <p>Возьмем какое-нибудь место на карте, в котором нет перепадов высот. Например, это (панорама).</p> <p><img src=$

В небольшой окрестности этой точки запросим все значения высот, которые приходили с Android-телефонов за какой-нибудь интервал времени. Построим гистограмму полученных высот. Интуиция и здравый смысл подсказывают, что гистограмма должна выглядеть как гауссиана. Но данным наплевать на нашу интуицию и здравый смысл:

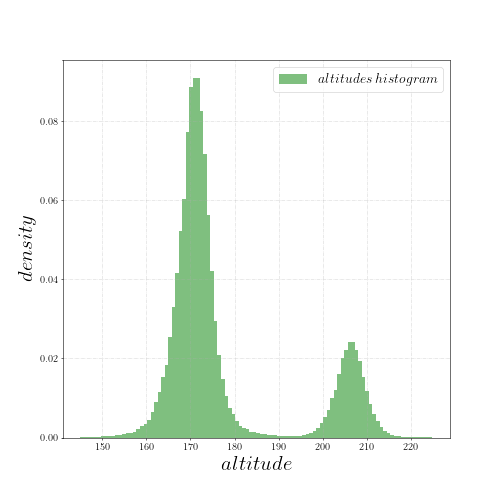
Значения высот разбились на два кластера-гауссианы. Расстояние между центрами этих кластеров около 35 метров. Но рядом нет никакой горы в 35 метров!

Кластеризуем значения высот (ого, мне наконец-то пригодился EM-алгоритм! :))

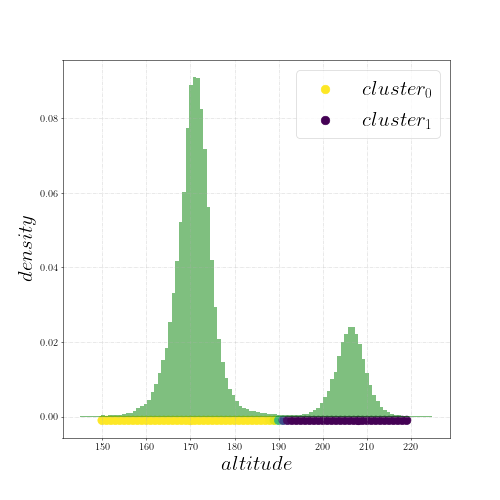
Кластеризация говорит, что во втором кластере лежит ~20% наблюдений. — основной. Авносит шум. То есть сейчас каждое пятое наблюдение вносит шум.

Данные (lat, lon, alt) высчитываются на устройстве из спутниковых сигналов и показаний других сенсоров телефона, а затем отдаются нам (почитать про разные приложения для измерения высоты).

Сырых наблюдений со спутников у нас нет, то есть телефон здесь для нас — чёрный ящик, который перемалывает сигналы GPS и показания других сенсоров в. Отсюда напрашивается очевидная гипотеза: один кластер чёрных ящиков перемалывает одним способом, а второй — другим. Например, одни Android«ы могут считать высоту относительно геоида, а другие — относительно эллипсоида WGS. Либо у одной группы телефонов у высоты один «ноль», а у другой группы — другой. Либо отвалился какой-то сенсор и есть режим работы без этого сенсора, который возвращает другие значения. Это мои догадки, они могут быть неправильными :)

Перейдем к фактам:
- Есть два кластера. Размер второго сильно меньше размера первого, но он нам портит жизнь, потому что вносит шум.
- Два кластера возникают из-за того, что черный ящик из-за каких-то факторов (версия чего-нибудь, отвалился/прицепился барометр, просто софт разный и т.д., сейчас это не важно) может вычислять высоту двумя разными способами.
- По имеющимся у нас данным с телефона мы не можем однозначно сказать, из какого кластера к нам пришла высота. Тут можно поверить мне на слово, что я перерыл все колонки во всех таблицах нашей базы и никакая идеально не разделила два кластера :)
- Маленький кластер нужно убрать!
Помимо значения высоты alt к нам так же приходит значение altitude accuracy. На самом деле, получаемая высота — это не точечное значение, а отрезок, в котором с некоторой вероятностью находится значение высоты.

То есть если к нам пришло alt = 50m и altitude accuracy=5m, это надо интерпретировать как «высота, вероятно, лежит в круге с центром 50 метров и радиусом 5 метром». Чем больше altitude accuracy, тем меньше смартфон уверен в отдаваемой высоте.

Рассмотрим такую гипотезу:

— телефон находится в нормальном состоянии.

— когда у телефона нет какого-то сенсора, например, не работает барометр. И из-за этого он вычисляет высоту другим способом.

Если у телефона что-то не работает, логично предположить, что он должен быть меньше уверен в значениях выдаваемых высот. То есть altitude accuracy` должно быть больше. Проверим это. Фильтранём высоты по $altitude \ accuracy < 4$ (в графиках с кластерами выше фильтровалось по $altitude \ accuracy < 10$ ):

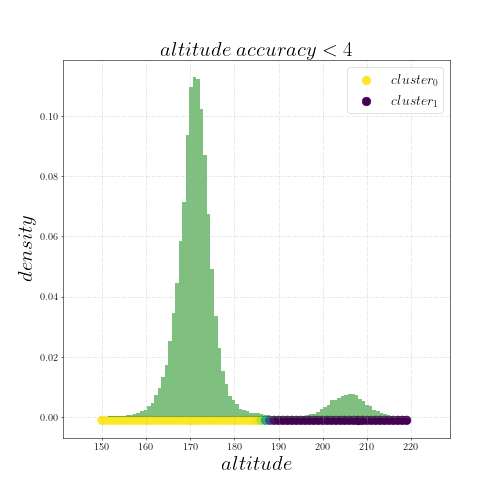
Огонь, горбик второго кластера стал меньше! Сейчас ~10% высот находятся во втором кластере, раньше было 20%. То есть для большого количество телефонов показания с большим altitude accuracy можно интерпретировать не как «высота такая-то© Habrahabr.ru