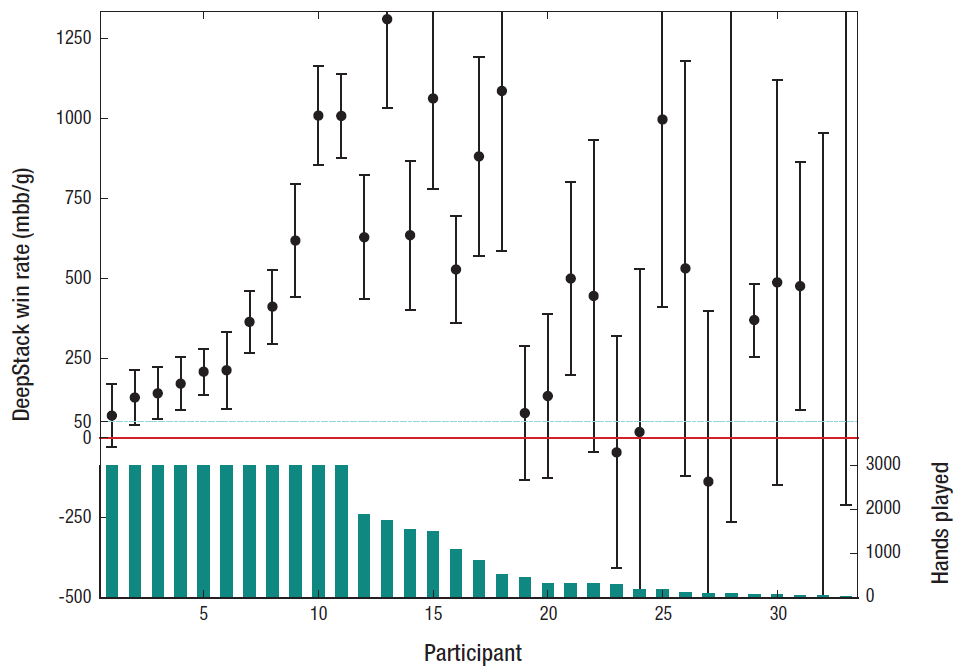
Покерная программа DeepStack обыгрывает профессионалов один на один
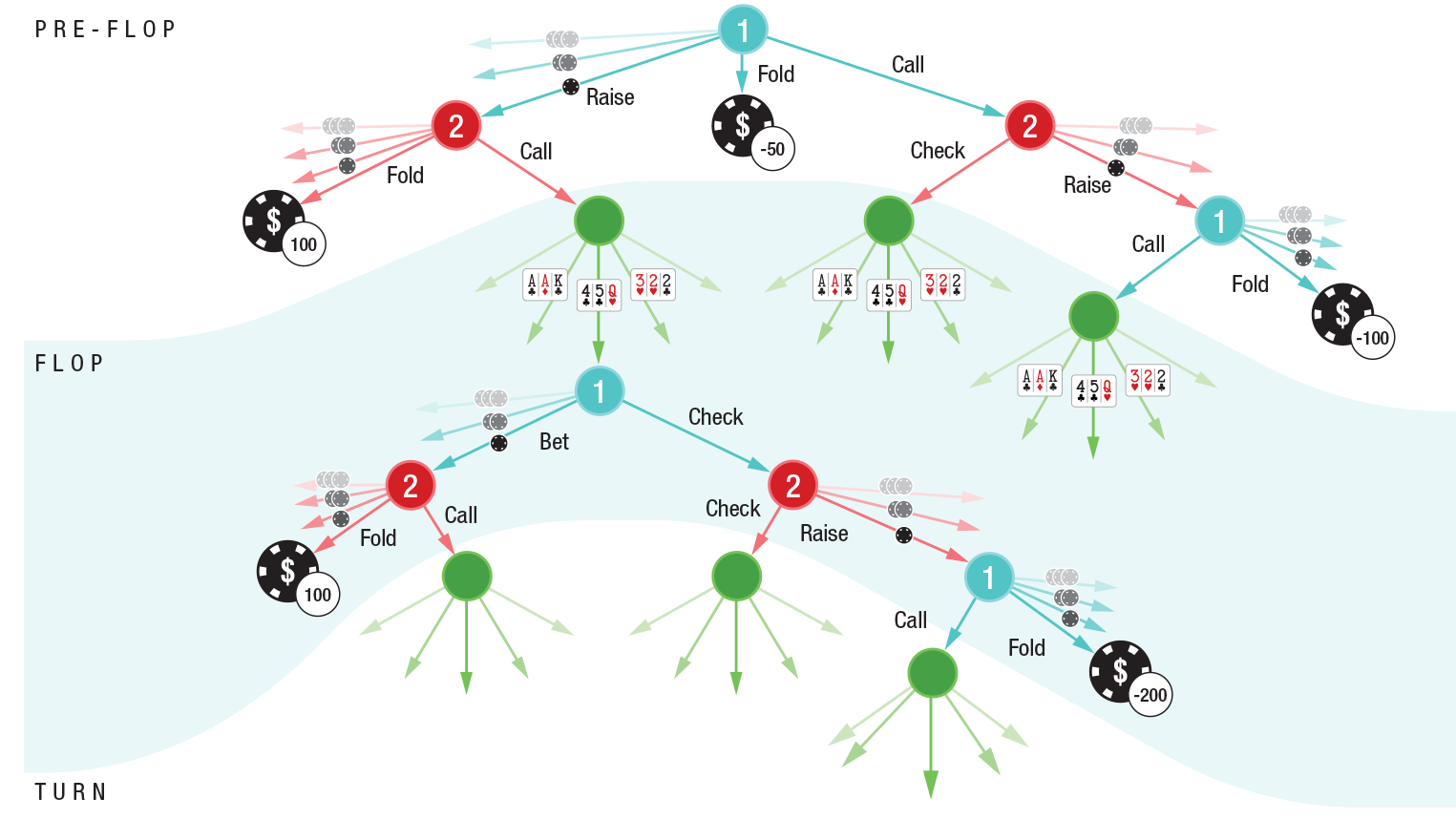
Дерево решений программы DeepStack в хедс-апе (игре один на один) безлимитного холдема на префлопе, флопе и тёрне
Пионер современной теории игр Джон фон Нейман говорил: «Реальная жизнь вся состоит из блефа, из маленьких приёмов обмана, из размышлений о том, каких действий ожидает от тебя другой человек. Вот что представляет игра в моей теории» (цитата из 13-й серии документального сериала «Возвышение человечества»).
Другими словами, Джон фон Нейман предвидел, что для создания сильного ИИ компьютер должен научиться играть в игры с неполной информацией, которые наиболее соответствуют человеческому поведению в реальной жизни. Такие игры как покер.
Настольные игры — традиционная область экспериментов в сфере искусственного интеллекта. С каждым годом ИИ обыгрывает человека в разные игры. Сначала сдались шашки, потом шахматы, затем видеоигры Atari, последней пала игра го. Но всё это игры с полной информацией, в которых все игроки имеют полную информацию о состоянии игры. Покер — совершенно другое дело.
Учёные давно пытаются разработать программу, которая бы могла обыгрывать человека в безлимитном Texas Holdem. В отличии от других применений слабого ИИ, здесь успешная разработка окупится мгновенно, потому что ежедневно в онлайновых покер-румах разыгрывают банки на миллиарды долларов.
Джон фон Нейман говорил, что покер восхищает его, и это совершенно неудивительно, учитывая уникальные особенности этой игры с неполной информацией. У каждого игрока есть только часть информации о состоянии игры — и он действует, исходя из этой частичной информации, а также оценивая действия других игроков.
Раньше ИИ добивался некоторого успеха только при игре в лимитный холдем, самый примитивный вариант игры с ограниченным шагом повышения ставок. В лимитном варианте у игрока есть всего лишь 1014 вариантов развития. Для сравнения, в безлимитном холдеме таких вариантов уже 10160. Кстати, в игре го вариантов развития 10170, но там игра с полной информацией, то есть принципиально более простая задача.
Игры с неполной информацией требуют совершенно более сложного уровня рекурсивного мышления, чем игры с полной информацией. Здесь правильное действие ИИ зависит в том числе от информации, которую ИИ получил от действий оппонента. Но информация, которую выдал оппонент, в свою очередь, является производной функцией от предыдущих действий ИИ и той информации, которую ИИ своими действиями выдал оппоненту. Это и есть рекурсивное мышление, с которым имеет дело программа DeepStack. И справляется она очень неплохо, судя по результатам игр с профессионалами (см. таблицу).
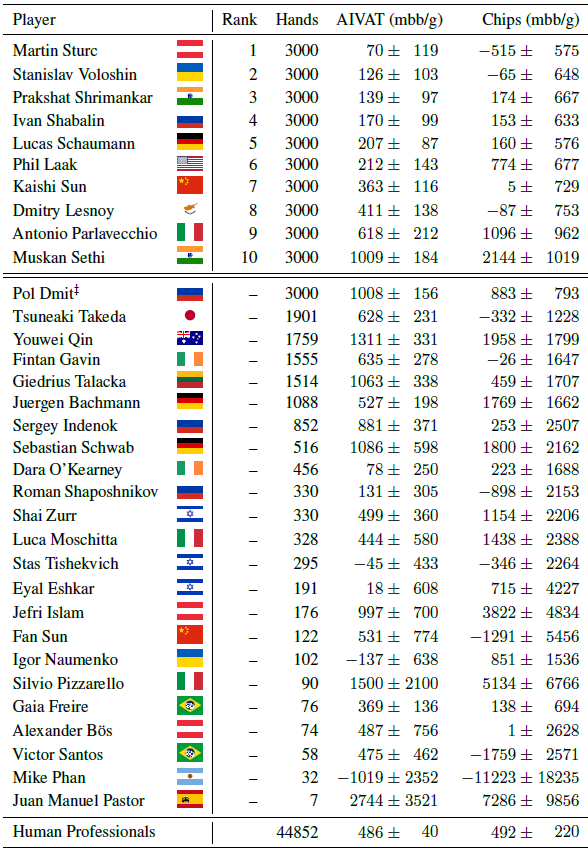
Результаты программы в хедс-апах с профессиональными игроками
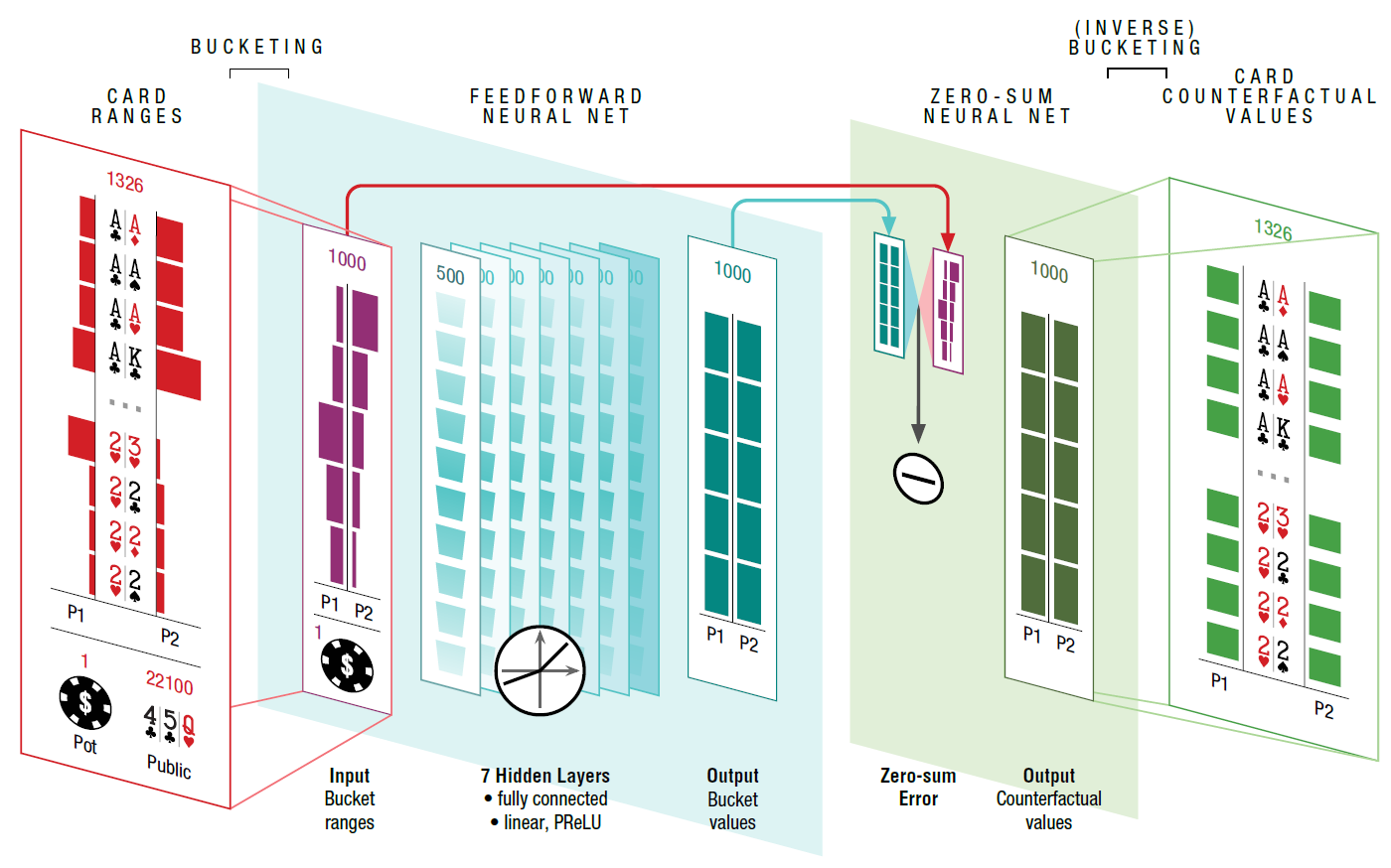
Архитектура программы DeepStack показана на иллюстрации. Программа переоценивает свои действия на каждом этапе, когда от неё требуется принятие решения. Для расчёта вэлью каждой ставки используется дерево предвидения (lookahead tree), значения для подветок которого вычисляются с использованием нейросети, заранее обученной на случайных игровых ситуациях.
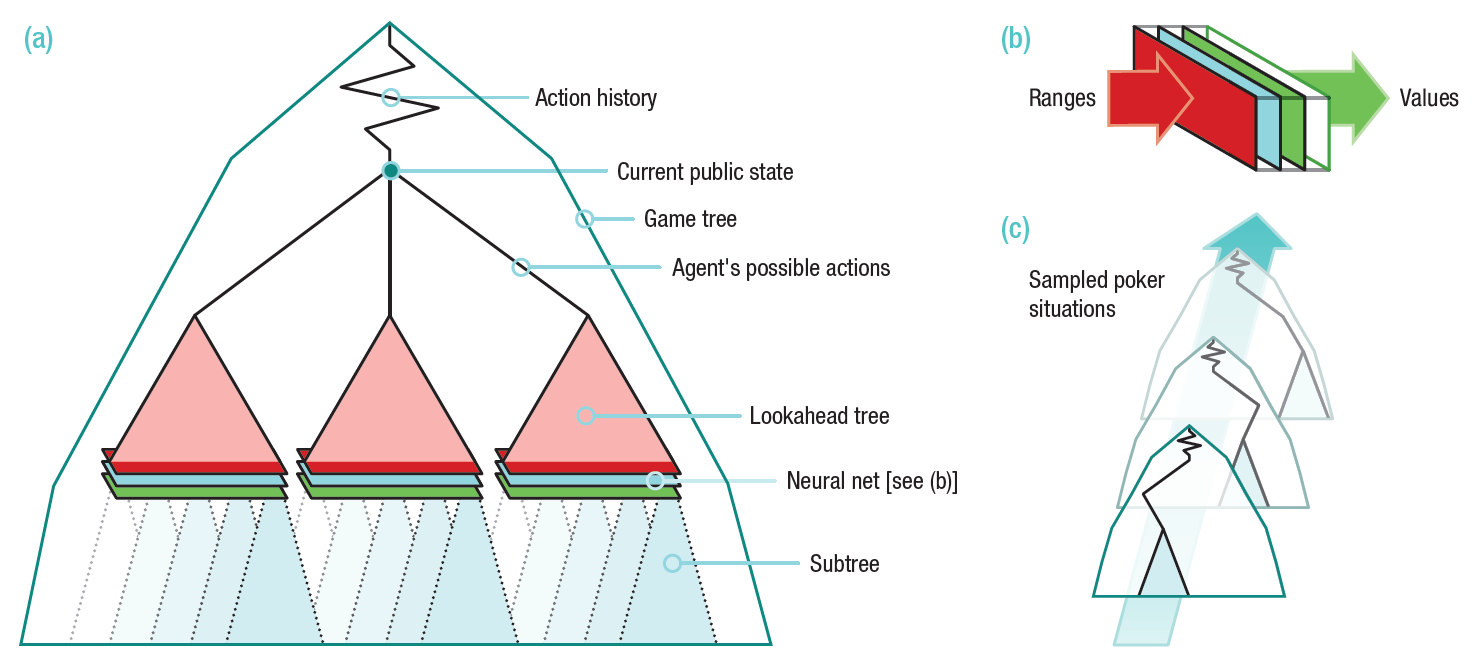
Структура нейросети демонстрирует, что на входе подаётся размер банка, открытые карты и диапазоны игроков (возможные комбинации, с которыми игрок мог войти в игру таким образом, каким он в неё вошёл (колл, рейз, 3-рейз и т.д.), вероятность каждой комбинации). Нейросеть состоит из семи полностью соединённых скрытых слоёв. Выходные значения затем обрабатываются другой нейросетью, которая проверяет, что действия удовлетворяют ограничению на нулевую сумму.
Особенностью программы является то, что она активно сопротивляется анализу своей стратегии со стороны оппонента. Другими словами, программа использует равновесие Нэша — ключевое понятие теории игр. Под равновесием Нэша подразумевается набор стратегий, котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют. С точки зрения антагонистической игры в покер основной задачей DeepStack является поиск равновесия Нэша, то есть минимизация возможности эксплуатации своей стратегии другим игроком для получения им прибыли. Абсолютно все разработанные до сегодняшнего дня покерные программы легко эксплуатировались после прощупывания их стратегии с помощью техники LBR (local best-response) — см. недавний обзор самых современных ботов для покера.
Так вот, DeepStack совершенно не эксплуатируется с помощью LBR. Вкупе с реальными результатами, которые показал бот в игре с профессионалами, остаётся только один вопрос: зачем разработчики опубликовали информацию об этой архитектуре в открытом доступе?
Научная работа опубликована 6 января 2017 года на сайте arXiv.org, где выкладываются статьи до выхода в официальном журнале.
Группой разработчиков руководит профессор информатики Майкл Боулинг из Университета Альберты (США).

Группа разработчиков DeepStack
Кафедра покерных ботов в Университете Альберты (Computer Poker Research Group) создана ещё в 90-е годы, первым созданным здесь ботом был Loki в 1997 году. Потом были Poki (1999), PsOpti/Sparbot (2002), Vexbot (2003), Hyperborean (2006), Polaris (2007), Hyperborean No-Limit (2007), Hyperborean Ring (2009), Cepheus (2015) и, наконец, венец творения — DeepStack.
В ближайшее время программу DeepStack проверят в играх с более опытными профессионалами, которые гораздо выше уровнем, чем ребята из таблицы в начале статьи. Начиная с этих выходных программа будет играть на турнире в питтсбургском казино, куда ожидается приезд нескольких профессионалов мирового класса. За 20 дней DeepStack должна сыграть около 120 000 рук. Это достаточно много, чтобы довольно точно оценить качество программы.
На данный момент DeepStack сыграл 44 852 руки против профессионалов добровольцев, отобранных Международной федерацией покера. Игроки получали денежные призы за хорошую игру (первый приз $5000 CAD), так что люди играли в полную силу. Тем не менее, программа в хорошем плюсе.