Поиск линии корешка на фотографиях книжных разворотов
 При съемке книжного разворота с помощью камеры мобильного устройства неизбежно возникают некоторые из нижеперечисленных дефектов (а возможно, что и все сразу):
При съемке книжного разворота с помощью камеры мобильного устройства неизбежно возникают некоторые из нижеперечисленных дефектов (а возможно, что и все сразу):
• цифровой шум,
• тени и блики,
• расфокусировка и смаз,
• перекос,
• перспективные искажения,
• кривые строки,
• лишние объекты в кадре.
Обработка таких фотографий для последующего OCR — довольно трудоемкая задача даже для человека, хорошо владеющего навыками работы в Photoshop. Как быть, если мы хотим это сделать автоматически, с помощью программы? Сразу оговоримся, что подробное описание всех этапов алгоритма сделало бы публикацию чересчур объемной, поэтому мы сейчас расскажем только о том, как решать одну из подзадач — найти линию корешка на таких фотографиях. О том, как устранять тени и блики на фотографиях мы уже рассказывали. Про устранение цифрового шума написано много статей. А про автоматическое исправление перспективы и кривых строк мы расскажем в следующий раз.
На первый взгляд, задача не представляет никакой сложности: выделяем все контуры на изображении с помощью одного из операторов градиента (например, Sobel) и ищем наиболее сильный и протяженный из них с помощью преобразования Хафа:


Нам нужно найти самый яркий пиксель на картинке справа и получить уравнение линии из его координат. И это все? Кто-то, возможно, решит, что можно еще сначала уменьшить картинку, чтобы не заниматься всем этим на изображении размером 5–10 мегапикселей. Но что-то подсказывает, что так просто это будет работать далеко не всегда. Рассмотрим возможные ситуации:
У корешка нет тени:

На странице есть фотография с темной рамкой:

Или просто большая темная фотография:

Таблица:

Многоколоночный текст с сепараторами:

В подобных ситуациях тривиальный алгоритм, приведенный выше, будет слишком часто ошибаться. Попробуем немного усовершенствовать его и учесть приведенные примеры.
Конвертируем изображение в полутоновое (серое) и применяем фильтр UnsharpMask со следующими параметрами: radius = 41, strength = 300.

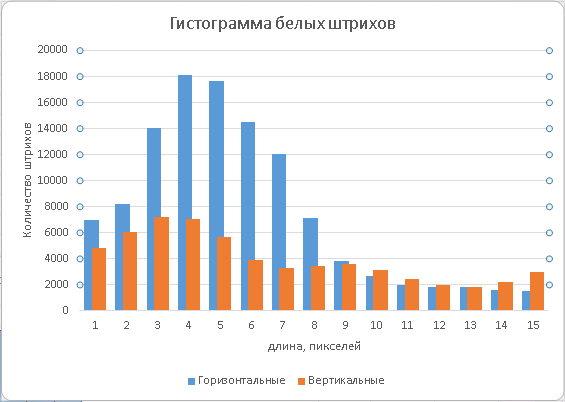
Чтобы определить, в каком направлении нам следует разрезать изображение, мы ищем направление строчек текста. Это можно сделать на бинаризованном изображении по гистограммам длин белых RLE-штрихов. Известно, что расстояние между строк как правило превосходит интервал между букв в многострочном тексте (иначе его было бы трудно читать). Гистограмму длин штрихов следует собирать по области изображения, содержащей текст. Можно использовать простейший классификатор текстовых блоков или просто отступить от краев изображения 10–15%, чтобы поля и фон не «затеняли» собираемую статистику. Обозначим сумму площадей горизонтальных белых штрихов, имеющих длину, не превосходящую некоторый порог L, как Sh, а сумму площадей вертикальных штрихов как Sv. Тогда, меняя порог L, можно следить за соотношением max (Sh, Sv) / min (Sh, Sv), и как только оно станет больше 2, мы можем с уверенностью сказать, что обнаружили межбуквенный интервал. А заодно и определили направление строк: если max (Sh, Sv) = Sh — оно горизонтальное, иначе — вертикальное. Мы взяли соотношение равным 2, чтобы не делать слишком много пропусков в определении ориентации и в то же время, не ошибаться слишком часто. Меняя эту величину можно получать разные точки на графике precision/recall. Можно использовать дополнительные признаки из тех же гистограмм. В тех случаях, когда нам не удается определить ориентацию однозначно простым способом, мы запускаем поиск сильной гипотезы корешка (тени) в обоих направлениях (горизонтальном и вертикальном) и оцениваем направление строк текста как перпендикулярное к направлению корешка, которое имеет более сильный отклик.
Предположим, на фотографии присутствует тень в области корешка. Подготовим изображение для поиска этой линии:
a) уменьшим изображение до заданного размера, например, до 800 пикселей по длинной стороне;
b) избавляемся от больших теней с помощью морфологической операции TopHat: вычитаем из исходного изображения его размыкание, т.е. наращивание от эрозии (r=5), под сигналом = 1 понимаем черное, а белый фон = 0;
c) убираем строчки (короткие вертикальные черные штрихи) с помощью эрозии по вертикали (r=3);
d) получив изображение строк как разницу между двумя предыдущими результатами, используем его как штраф, прибавив к текущему.
a) 
b) 
c) 
d) 
К последнему изображению применяем быстрое преобразование Хафа и ищем глобальный максимум на инвертированном изображении:

Можно учесть при этом статистическое распределение по углу от вертикали и смещению по горизонтали линии корешка. Как правило, в 99.9% случаев угол не превосходит по модулю 20–25 градусов, а середина линии корешка имеет координату от w/3 до 2w/3 (w — ширина изображения). При этом крайние значения углов и координат имеют гораздо меньшую вероятность, чем средние. Можно учесть это распределение в значениях точек в пространстве Хафа, накладывая штраф за отклонение от наиболее вероятного положения по углу и координате (0, w/2).
Если найденный глобальный максимум превосходит порог обнаружения сильной гипотезы, считаем, что мы нашли линию корешка по тени. В этом случае преобразуем координаты максимума в уравнение линии. Величину порога мы подбираем экспериментально на большой выборке фотографий, минимизируя количество ошибок и пропусков.
При подобранном значении порога, примерно в 10% случаев сильная гипотеза не находит решения. Как мы знаем, тень может отсутствовать в области корешка. Это может произойти при сильном раскрытии разворота или если использовалась вспышка при съемке. Попробуем найти линию корешка в области центрального просвета.
Вычисляем модуль градиента (b) на уменьшенном полутоновом изображении (a) (оператор Sobel):
a) 
b) 
Здесь специально выбран другой пример, т.к. наличие сильной тени будет мешать этому алгоритму.
На бинаризованном изображении c) склеим текст в блоки с помощью морфологической операции дилатации (d, r=6 для изображения размером 800 пикселей). Применим полученную маску текстовых областей к изображению модуля градиента (e, сигнал был усилен в 4 раза).
c) 
d) 
e) 
А теперь сгладим маску текстовых областей (d) гауссовым размытием (f) (r=8) и добавим к ней полученный усиленный градиент нетекстовых областей (g).
f) 
g) 
Теперь мы получили изображение, где линия корешка, если она содержит в себе хотя бы слабый градиент, дает дополнительный вклад в сигнал области просвета. Если же градиент отсутствует, т.е. нет видимой линии на изображении, то мы за счет гауссового размытия выберем линию, достаточно удаленную от текста с обоих сторон. При нешироком корешке она пройдет примерно посередине.
Для поиска линии будем опять применять преобразование Хафа, и искать глобальный максимум с учетом статистического распределения по углу и смещению:

Координаты максимума преобразуем в уравнение линии корешка. Готово!
Приведенный несложный алгоритм на имеющейся в нашем распоряжении базе в >1800 фотографий книжных разворотов дает менее 1,5% ошибок.
Разумеется, есть много возможностей для его улучшения: можно выделять дополнительные признаки на изображении, вычислять не две гипотезы последовательно, а несколько и сразу, оценивать их взаимное расположение, выделять объекты на изображении (строки, сепараторы) и заниматься их анализом… В какой-то момент возникнет потребность в очередной раз расширить обучающую (и тестовую!) выборку, чтобы избежать возможного переобучения. Все это — бесконечная борьба за качество алгоритма.
Решая задачу поиска линии корешка, мы забыли сказать, а зачем вообще нам было это нужно? Зачем нужно на фотографии искать эту линию? Очень просто: линия корешка позволяет устранить перекос, т.е. повернуть изображение так, чтобы эта линия стала вертикальной, она разделяет изображение на две страницы для последующего применения алгоритма разгибания строк, помогает определить перспективные искажения (правда, для этого нужно будет найти еще точки схода перспективы). В общем, не решив эту задачу, подготовить подобные фотографии для последующего OCR едва ли возможно. Эти алгоритмы уже нашли свое применение в технологии BookScan, которая является частью нашего мобильного приложения ABBYY FineScanner.
