Поговорим об оптимизирующих компиляторах. Сказ первый: SSA-форма
Всем привет. Сегодня я хотел бы поговорить об устройстве современных оптимизирующих компиляторов. Я никогда не публиковался на Хабре ранее, но надеюсь, что мне удастся написать серию статей, которая просуммирует мой опыт в этой области.
Коротко обо мне. Меня зовут Макс, и так получилось, что я вот уже 10 лет, почти с самого начала своей карьеры, занимаюсь оптимизирующими компиляторами. Я начинал в Intel, потом перешёл в Azul Systems, год провёл в Cadence и вернулся обратно, всё это время занимаясь компиляторными оптимизациями для Java, C++ и нейросетевых моделей. На момент написания статьи у меня чуть за 900 патчей в LLVM, большинство из них посвящено цикловым оптимизациям.
За это время я провёл десятки собеседований на позиции как интернов, так и инженеров сеньорного уровня, и довольно часто люди, приходя на эти собеседования, многих вещей не знают или знают поверхностно. И я подумал:, а мог бы я написать такой цикл статей, чтобы человек, прочитав их, узнал бы всю ту базу, которая, на мой собственный взгляд, необходимо начинающему компиляторному инженеру? Очень бы хотелось, чтобы новичку в этой области можно бы было дать один (относительно небольшой по объёму) набор текстов, чтобы он получил оттуда всё необходимое для старта. Это не перевод, текст оригинальный, поэтому в нём могут быть ошибки и неточности, которые я буду рад исправить, если вы мне их укажете.
Итак, поехали.
Что такое SSA-форма
Наверное, все, кто хоть немного сталкивался с компиляторами, в курсе, что они обычно делают оптимизации не на исходном коде (написанном на С++, Java или, прости господи, на Haskell), а на некотором внутреннем представлении, которые обычно основаны на графах. Многие в курсе, что есть такая вещь, как AST (абстрактное синтаксическое дерево), которая вполне годится для некоторых этапов работы компилятора, но оптимизировать AST — достаточно неудобно (хотя и возможно, особенно если речь идёт о простых локальных оптимизациях). К тому же, конструкции AST так или иначе привязаны к языку, и если стоит задача построения универсального оптимизирующего компилятора для нескольких языков, то оно становится для этих целей совсем не пригодным.
Современные компиляторы решают эти проблемы путём добавления ещё одного уровня абстракции — промежуточного представления, или IR (англ. Intermediate Representation). Видов IR существует несколько, но мы подробно остановимся на тех, что основаны на SSA-форме (англ. Single Static Assignment form). Опыт и практика показали, что на них многие оптимизации делаются легко и приятно, и именно на ней основан LLVM IR, который лежит в основе компиляторов языков C++ (clang), Rust, Objective-C, Haskell, Kotlin Native, тысячи их. Есть даже компилятор Falcon в Azul Prime VM, который делает это для Java. Наверное, это не самый совершенный IR, какой может быть, но это лучшее, что есть у нашего человечества. Здесь и далее все примеры будут иллюстрироваться именно на LLVM IR, хотя это не единственный IR, основанный на SSA.
Итак, у Single Static Assignment формы есть следующие свойства:
Программа состоит из инструкций, которые могут использовать (use) и определять (def) новые значения. Каждое определяемое значение имеет уникальное имя и не может быть переопределено.
Инструкции привязаны к базовым блокам, образующим граф потока управления, или CFG (англ. Control Flow Graph), и исполняются при входе в соответствующий блок.
Инструкция может использовать только те значения, которые гарантированно вычислены к моменту её исполнения.
Для того, чтобы слить значения из разных ветвей CFG, используется специальная инструкция, называемая Φ-узлом (англ. Phi node). Это не русская «Ф», это греческая «фи».
Теперь давайте пройдёмся по этим пунктам и объясним каждый из них.
Значения определены лишь однажды
Рассмотрим простую функцию без каких-либо условных переходов. У нас есть просто линейный кусок кода, который проводит некоторые действия над переменными. Пример на С++:
int ssa_example(int a, int b) {
int sum = a + b;
sum = sum + 1;
a++;
sum += a;
sum += b;
return sum;
}В этой программе у нас есть 3 переменные (a, b, sum), причём некоторые из них несколько раз меняют свои значения. В SSA-форме запрещено переопределять значения переменных. Чтобы представить себе, как это работает, вообразите, что заказчик (злобный тимлид, коварные рептилоиды) запретил вам в целях безопасности использовать какие-либо переменные, кроме const (но при этом все те же операции должны производиться над такими же значениями в том же порядке). С таким требованием вы бы переписали эту программу примерно вот так:
int ssa_example(const int a_0, const int b_0) {
const int sum_0 = a_0 + b_0;
const int sum_1 = sum_0 + 1;
const int a_1 = a_0 + 1;
const int sum_2 = sum_1 + a_1;
const int sum_3 = sum_2 + b_0;
return sum_3;
}Просто всякий раз, когда нам нужно было переприсвоить переменную (чего мы теперь не можем делать) мы должны определить новую переменную и в дальнейшем пользоваться ей. С точки зрения С++, выглядит довольно многословно и бредово, и ни один человек в здравом уме так не будет писать. Но ведь мы стараемся не для человека, а для компилятора!
В таком виде программа имеет ценное преимущество: если вы видите использования одной и той же переменной в разных местах программы, вы точно знаете, что имеете дело с одним и тем же значением. Никакая инструкция ни в каком другом месте программы не могла его изменить. Рассмотрим известную оптимизацию «Удаление общих подвыражений», или CSE (англ. Common Subexpression Elimination). Представьте, что ваша программа написана на обычном С++, и где-то в двух разных местах вы видите код:
int x = a + b;
...
int y = a + b;Можете ли вы не вычислять y, а вместо него везде использовать ранее посчитанное значение x? Да, но только в случае, если между этими двумя точками никто не поменял значения a или b. Если ваша программа записана в SSA-форме, то этот факт у вас есть автоматически, а в противном случае вам потребуется какой-то анализ, который пройдёт по инструкциям между этими двумя точками и поймёт, менялись ли a и b. Это не единственная причина, почему оптимизаторы любят SSA, и о них мы поговорим как-нибудь в другой раз. Пока просто примем на веру, что это удобно.
Напоследок, вот как аналогичная программа будет выглядеть на LLVM IR, который соответствует SSA-форме:
define i32 @ssa_example(i32 %a_0, i32 %b_0) {
%sum_0 = add i32 %a_0, %b_0;
%sum_1 = add i32 %sum_0, 1;
%a_1 = add i32 %a_0, 1;
%sum_2 = add i32 %sum_1, %a_1;
%sum_3 = add i32 %sum_2, %b_0;
ret i32 %sum_3;
}Думаю, всё достаточно интуитивно и очень похоже на С++ с константными переменными. Написать второй раз %sum_2 = … было бы семантической ошибкой.
Базовые блоки и CFG
Базовый блок — это линейный кусок кода, который исполняется последовательно, без передачи управления каким-либо другим инструкциям изнутри блока. Вы не можете ни прыгнуть в середину базового блока, ни из середины блока: зайдя в его начало, вы исполняете его весь целиком до конца*, и в конце переходите в другой блок. Фактически, любая конструкция для описания условного перехода (if, switch, goto, do-while, for, …) приводит к появлению новых базовых блоков.
Представим ориентированный граф, вершины которого — это базовые блоки, а дуги соответствуют переходам между ними. Это и есть наш CFG. При этом один (входной, entry) блок в нём является особенным: с него начинается исполнение. Рассмотрим функцию на С++:
int cfg_example(int a, int b) {
if (a + 1 < b) {
a += b;
} else {
do {
b *= a;
} while (b < 100);
}
return (a + 7) * (b + 10);
}Вот как будет выглядеть её CFG:
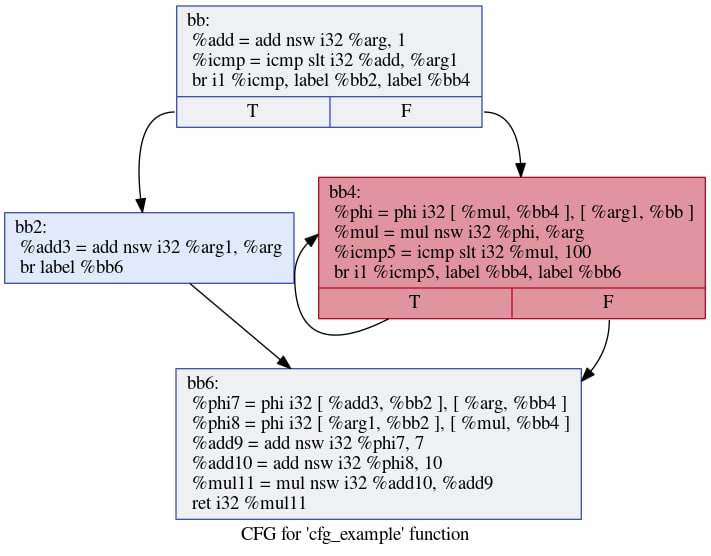
Содержимое блоков мы обсудим позже, важно то, что здесь видно, как выглядит ветвление и как выглядит цикл. Читатель, знакомый с языком ассемблера, наверное, заметил аналогию между этим представлением и лейблами/jmp-инструкциями, и эта аналогия совершенно верная. В текстовом виде LLVM IR выглядит очень похоже на чуть-чуть более высокоуровневый ассемблер, и лейблам соответствуют имена базовых блоков.
define i32 @cfg_example(i32 noundef %arg, i32 noundef %arg1) {
bb:
%add = add nsw i32 %arg, 1
%icmp = icmp slt i32 %add, %arg1
br i1 %icmp, label %bb2, label %bb4
bb2: ; preds = %bb
%add3 = add nsw i32 %arg1, %arg
br label %bb6
bb4: ; preds = %bb4, %bb
%phi = phi i32 [ %mul, %bb4 ], [ %arg1, %bb ]
%mul = mul nsw i32 %phi, %arg
%icmp5 = icmp slt i32 %mul, 100
br i1 %icmp5, label %bb4, label %bb6
bb6: ; preds = %bb4, %bb2
%phi7 = phi i32 [ %add3, %bb2 ], [ %arg, %bb4 ]
%phi8 = phi i32 [ %arg1, %bb2 ], [ %mul, %bb4 ]
%add9 = add nsw i32 %phi7, 7
%add10 = add nsw i32 %phi8, 10
%mul11 = mul nsw i32 %add10, %add9
ret i32 %mul11
}Φ-функция
На рисунке выше видно, что в зависимости от значения входных параметров мы могли пойти по разным путям. Например, при некоторых входных данных мы могли пройти по пути %bb ➝ %bb2 ➝ %bb6, а могли — по пути %bb ➝ %bb4 ➝ %bb4 ➝ %bb4 ➝ %bb4 ➝ %bb6.
Давайте взглянем на исходную программу. Если мы зашли в if, то у нас поменяется значение a (т.е. мы объявим новое SSA-значение для a, в данном случае %add3). При этом блок %bb4 никогда не исполнялся. В то же время, если мы зашли в else, то поменялось значение b (для него мы создали инструкцию %mul), но при этом мы не заходили в %bb2.
В то же время, в заключительном блоке %bb6 нам нужны значения и для a, и для b. Интуитивно все понимают, что нельзя использовать результат той инструкции, которая не исполнялась, этого значения просто нигде нет. И нужно как-то выразить тот факт, что значения a и b могли измениться, а могли и не измениться в зависимости от того, как мы пришли в финальный блок. Более того, в цикле значение b могло поменяться несколько раз, и это тоже нужно как-то выразить.
Здесь мы сталкиваемся с понятием Φ-функции и соответствующей инструкцией (буду её называть phi-нодой по привычке). Они всегда вычисляются в начале базового блока по следующим правилам:
Φ-функция содержит набор пар вида [значение, блок-предшественник]. Для каждой такой пары значение обязано быть доступным (т.е. эта инструкция точно исполнилась) в соответствующем блоке-предшественнике.
Если мы приходим в данный блок из некоторого предшественника, то значение phi-ноды равно соответствующему значению из пары.
Все Phi-ноды вычисляются одновременно, независимо друг от друга, при входе в блок и до исполнения какой-либо другой инструкции.
Таким образом, инструкцию:
%phi7 = phi i32 [ %add3, %bb2 ], [ %arg, %bb4 ]следует читать так: «Если мы пришли в данный блок из блока %bb2, то %phi7 равно %add3, а если мы пришли из %bb4 — то %phi7 равно %arg. Нетрудно заметить, что %arg — это стартовое значение переменной a, а %add3 — это значение a после захода в if. Это полностью соответствует семантике изначальной программы на С++.
Аналогичным образом следует понимать и Phi-ноду, моделирующую изменение b в цикле:
bb4: ; preds = %bb4, %bb
%phi = phi i32 [ %mul, %bb4 ], [ %arg1, %bb ]
%mul = mul nsw i32 %phi, %arg
%icmp5 = icmp slt i32 %mul, 100
br i1 %icmp5, label %bb4, label %bb6Если мы вошли в данный цикл впервые из блока %bb, то значение %phi равно %arg1 (т.е. стартовому значению b). Если же мы пришли сюда из %bb4 (то есть прошли по обратной дуге цикла), то %phi равна результату умножения на a (которое равно %arg). Заметьте также, что в самом умножении фигурирует не %arg1 (стартовое значение b), а именно %phi (текущее значение b). Так, несмотря на запрет переприсваивать значения, SSA-форма может моделировать многократно меняющиеся значения. Классический пример — счётчики в for-циклах, которые также моделируются phi-нодой (её ещё называют индукционной переменной, и об этом мы поговорим как-нибудь в другой раз).
Итак, осталось свойство про одновременное обновление. По своему опыту могу сказать, что даже люди, много лет работающие с компиляторами, довольно часто об этом не задумываются или просто не знают. На самом деле, в большинстве случаев отсутствие или наличие порядка вычисления Phi-нод ни на что не влияет (они обычно друг от друга не зависят), но есть один интересный пример, который я люблю давать кандидатам на собеседованиях. Давайте рассмотрим такую программу:
int swap_example(int a, int b, unsigned n) {
for (unsigned i = 0; i < n; i++) {
int swap = a;
a = b;
b = swap;
}
return a;
}Если вы скомпилируете её при помощи clang, то увидите что-то вроде:
define dso_local noundef i32 @swap_example(i32 noundef %arg, i32 noundef %arg1, i32 noundef %arg2) local_unnamed_addr #0 {
bb:
br label %bb3
bb3: ; preds = %bb3, %bb
%phi = phi i32 [ %arg1, %bb ], [ %phi5, %bb3 ]
%phi4 = phi i32 [ 0, %bb ], [ %add, %bb3 ]
%phi5 = phi i32 [ %arg, %bb ], [ %phi, %bb3 ]
%add = add i32 %phi4, 1
%icmp = icmp eq i32 %phi4, %arg2
br i1 %icmp, label %bb6, label %bb3
bb6: ; preds = %bb3
ret i32 %phi5
}При внимательном рассмотрении тут есть кое-что, что кажется странным и часто сбивает с толку тех, кто забывает о последнем свойстве Phi-нод. Давайте разберём SSA-значения, которые мы тут видим:
Пара %phi4 и %add моделирует счётчик цикла и используется для сравнения с n.
%phi5 моделирует a, %phi моделирует b.
Возникает сразу два вопроса:
Куда делась переменная swap? Почему для неё нет никакой инструкции или хотя бы Phi-ноды?
Нет ли здесь ошибки? Ведь %phi использует в качестве одного из входов %phi5, и наоборот!
%phi = phi i32 [ %arg1, %bb ], [ %phi5, %bb3 ]
...
%phi5 = phi i32 [ %arg, %bb ], [ %phi, %bb3 ]С первой итерацией всё понятно: тут значения равны стартовым значениям, т.е. параметрам функции: %phi = b,%phi5 = a. Но что происходит, если мы идём на вторую итерацию? Если мы сначала присвоим %phi = %phi5 = b, а потом %phi5 = %phi = b, то обе фи-ноды получат одно и то же значение. Если мы переставим их местами и будем следовать той же логике, то они обе станут равны a, а это совсем не то, чего мы хотим.
Правильная же интерпретация тут состоит в том, что Phi-ноды используют именно значения на входе в блок, а не те, которые как бы уже вычисляются в блоке (т.е. не другие ранее вычисленные Phi). Таким образом правильно сказать так: при проходе по обратной дуге %phi станет равно тому, чему было равно %phi5 на входе в блок (т.е. в данном случае a — на второй итерации), а %phi5 станет равно тому, чему было равно %phi на входе в блок (т.е. b — на второй итерации). В таком случае эти две инструкции действительно меняются значениями каждые две итерации, и swap оказывается просто не нужен. Он не представляет никакое новое значение.
На самом деле, Phi-ноды — это самая сложная и самая объёмная часть при любом разговоре об оптимизациях. Им будут посвящены следующие тексты. В том числе я расскажу о том, как формализовать понятия «доступности» значений в той или иной точке, что такое доминирование и как оно помогает найти места для вставки Phi-нод.
На сегодня всё. Благодарю за внимание, и до новых встреч!
* Если только там не будет чего-то типа System.exit (), на котором всё закончится, но для нашего рассказа это неважно.
