Подробнее о разработке софта рентгеновского томографа18.05.2016 15:03

Ученые из Томского государственного университета создали микротомограф. Томограф позволяет с точностью до микрона узнать о внутренней структуре различных материалов, например, алмазов.

Но ведь интереснее в него запихнуть муху.

Перед EDISON Software Developement поставили задачу написать софт для микротомографа. О том, как они успешно справились с задачей, была статья на Хабре (Как за 5233 человеко-часа создать софт для микротомографа) с описанием алгоритмов, математических методов, реализации и отладки.

Ненасытные читатели засыпали нас вопросами, на которые мы, наконец-то, сформулировали ответы…
Томограф может просветить материал с разрешением до микрона. Это в 100 раз тоньше человеческого волоса. После сканирования программа создает 3D-модель, где можно посмотреть не только на внешнюю сторону детали, но и узнать, что у нее внутри.

Вопрос №1

С удовольствием бы почитал про обращение преобразования Радона с точечным источником и о реализации этого всего с использованием CUDA Uranix

Расчет Радона для точечного источника, если описать схематически, аналогичен расчету для параллельного режима, но только направление лучей не параллельно, что влияет на координаты точек в кубе объекта, куда прибавляются плотности. При таком схематическом описании, с точки зрения реконструкции, нет большой разницы, какой алгоритм использовать, меняются только координаты отрезков/лучей и формула их расчета.

Далее, когда на основе теневой проекции мы получили лучи от источника до каждой точки проекции в пространстве координат микротомографа, зная положение вращающегося куба объекта, вдоль каждого из лучей рассчитываются воксели, лежащие на луче. Каждому вокселю присваивается значение плотности пикселя теневой проекции, в которую входит луч от источника, тип данных весов преобразован к float. В итоге для каждой теневой проекции повторяем эту операцию проецирования на воксели с учетом угла проекции. После этого все суммарные значения вокселей нормализуются к разрядности, в которой они будут храниться в дальнейшем, обычно это было 16-битное целое беззнаковое. Данное описание максимально упрощенно объясняет схему реконструкции и получения конечной воксельной модели, далее приведено более подробное описание этого алгоритма.

Рентгеновская система генерирует плоское теневое изображение полной внутренней объемной структуры образца, но в отдельной теневой проекции глубинного распределения структур образца полностью смешиваются. Только рентгеновская томография позволяет визуализировать и измерить пространственные структуры образцов без их химической и механической обработки.

Рис. 1. Геометрия параллельных пучков

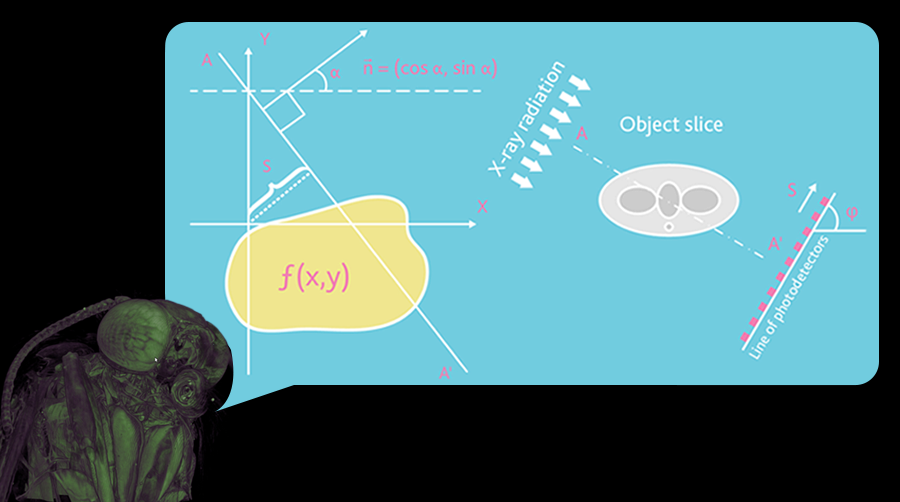
Любое рентгеновское теневое изображение является плоской проекцией трехмерного объекта. В наиболее простом случае мы можем описать его, как изображение, полученное в параллельных рентгеновских лучах (Рис. 1). В данном приближении каждая точка теневого изображения содержит суммарную информацию по адсорбции конкретного рентгеновского пучка на всем объеме трехмерного объекта. Для параллельной геометрии рентгеновских пучков реконструкция объемного изображения образца из двухмерной теневой проекции реализуется с помощью реконструкций серии двухмерных срезов образца вдоль одномерных теневых линий. Возможность такого рода реконструкций демонстрируется на простом примере: рассмотрим объект с единственной точкой с высокой адсорбцией в неизвестном месте.

Рис 1.1. Схематическое изображение трех различных положений поглощающей области и соответствующая реконструкция из полученных теневых проекций

В одномерной теневой линии будет наблюдаться уменьшение интенсивности вследствие ее поглощения на адсорбирующем объекте (Рис. 2). Теперь мы можем смоделировать в компьютерной памяти пустой ряд пикселей (элементов изображения), соответствующий предполагаемому смещению объекта. Естественно, следует удостовериться, что все части реконструируемого объекта будут находиться в поле зрения. Поскольку мы имеем координаты теней от поглощающих областей объекта, мы можем выделить в реконструируемой области в памяти компьютера все возможные положения поглощающих областей внутри объекта в виде линий. Теперь начнем вращать наш объект и повторять эту операцию. В каждом новом положении объекта мы будем добавлять к реконструируемой области линии возможных положений объекта в соответствии с положением его теневых проекций. Эта операция называется обратным проецированием. После нескольких оборотов мы можем локализовать положение поглощающей области внутри объёма реконструкции. С увеличением числа теневых проекций с различных направлений, эта локализация становится все более четкой (Рис. 3).

Рис. 2. Реконструкция точечного объекта с использованием различного числа смещений

В случае реконструкции на основании бесконечного числа проекций получается изображение с хорошей четкостью определения позиции области поглощения внутри исследуемого объекта. В то же время точечное изображение будет сопровождаться размытой областью, поскольку оно было получено в ходе наложения линий со всеми возможными отклонениями. Теперь, поскольку нам известно, что изображение образовано точечным объектом, мы можем провести предварительную коррекцию начальной информации в линиях сорбции чтобы сделать конечное изображение более соответствующим реальному объекту. Эта коррекция добавляет некоторое количество негативной адсорбции по внешней границе точки, чтобы убрать смазанность, присущую процессу обратного проецирования (Рис. 4). Этот алгоритм дает не только изображения сечений отдельных точечных структур, но и позволяет исследовать реальные объекты. Каждый материальный объект может быть представлен как большое количество отдельных элементарных поглощающих объемов и линейная адсорбция в каждом рентгеновском пучке соответствует суммарной адсорбции на всех поглощающих структурах, встреченных пучком.

Рис. 3. Фильтрация обратной проекции

Таким образом, двухмерные сечения объекта могут быть восстановлены из одномерных теневых линий с различных ракурсов. Однако, большинство рентгеновских излучателей не способны генерировать параллельные пучки излучения. В реальности используются точечные источники, производящие конические пучки рентгеновского излучения.

Рис. 4. Геометрия расходящегося пучка

В веерной геометрии реконструированные сечения будут иметь некоторые искажения в областях, удаленных от оптической оси пучка. Для решения этой проблемы мы должны использовать алгоритм трехмерной реконструкции конического пучка (Фельдкамп), чтобы принимать во внимание толщину объекта. Другими словами, лучи, проходящие сквозь фронтальную и заднюю поверхности объекта, не будут спроецированы на тот же ряд детектора (Рис. 6). Таким образом, наиболее быстро реконструируемым сечением является осевое сечение, поскольку оно не требует коррекции на толщину образца.

Рис. 5. Геометрия конического пучка

В случае рентгеноскопии образца изображение содержит информацию об уменьшении интенсивности падающего излучения внутри объекта. Поскольку поглощение рентгеновских лучей описывается экспоненциальной зависимостью (закон Ламберта-Бира), линейная информация об адсорбции излучения из теневого изображения может быть раскрыта с использованием логарифмической функции. Поскольку логарифмирование является нелинейной операцией, то малейший шум в сигнале приводит к значительным ошибкам в реконструкциях. Для избавления от такого рода ошибок может быть использовано усреднение начальных данных. С другой стороны, мы могли бы попытаться улучшить отношение сигнал-шум в теневом изображении с помощью оптимизации времени выдержки для накопления наиболее репрезентативной информации. Наиболее эффективным путем шумоподавления в процессе реконструкции является правильный выбор функции коррекции/фильтрации для конволюции перед обратным проецированием. В простейшем случае (описанном выше) функция коррекции производит две реакции негативной адсорбции вокруг любого пика сигнала или шума в теневой линии, и такое поведение становится весьма опасным при работе с шумным сигналом. Выбор для проведения коррекций функции конволюции со спектральными ограничениями (окно Хамминга) позволяет решить эту проблему.

Описание работы CUDA и реконструкции

Реконструкция данных по теневым проекциям
Максимальный размер куба для реконструкции 1024×1024x1024 вокселя. Назовем такой куб единичным. Алгоритм позволяет реконструировать меньшие кубы, но при этом размерность по всем направлениям должна быть кратна 32. За один подход реконструируется слой куба, объемом не более 128 МБ, т.е. 1/8 единичного куба. Если в системе установлено несколько CUDA устройств, то реконструкция на них будет идти параллельно.

Загрузка в RAM теневых проекций производится при первом проходе, в объеме достаточном для реконструкции куба. Т.е. если для реконструкции куба требуется 1200 строк из теневой проекции, а высота файла 2000, то именно эти 1200 строк данных из файла загружаются в RAM и кэшируются. Поскольку при реконструкции следующего куба, скорее всего, сегменты проекции будут пересекаться, можно будет использовать уже загруженные данные повторно, догрузив лишь новые строки.

Обнаружение серверов и распределение задач
Для обнаружения клиентов и серверов используется широковещательная рассылка UDP пакетов. При старте и каждые 5 секунд сервер рассылает такое уведомление. Клиент при старте рассылает широковещательный запрос, который заставляет объявить о себе сервер немедленно. Клиент, получив уведомление о присутствии сервера, устанавливает с ним TCP соединение, по которому происходит отсылка команд управления, задач, и получение уведомлений о завершении задачи. Все клиенты, сервера, задачи обладают уникальным идентификатором.

При разрыве соединения с одним сервером считается, что сервер остановился, и его задачи перераспределяются среди других. При подключении нового сервера задачи от других не отбираются и не перенаправляются на него. Поэтому для равномерной загрузки важно обнаружить все сервера к началу распределения задач реконструкции. По мере готовности кубиков становится возможен запуск задач объединения. Задачи направляются на случайный сервер. Задачи реконструкции и объединения выполняются серверами параллельно.

Задачи могут поступать от нескольких клиентов. Сервер обрабатывает их в порядке поступления (FIFO). Клиент предпочитает раздавать задачи реконструкции из одного слоя единичных кубиков на один сервер, чтобы уменьшить объем данных, необходимых серверу реконструкции. Объем оперативной памяти сервера определяет стратегию реконструкции и сжатия кубиков. Если памяти много (более 20 ГБ), то сжатие предыдущего кубика и реконструкция следующего осуществляются параллельно, иначе реконструкция следующего кубика не начинается, пока куб не будет полностью обработан, т.е. сжат и сохранен на диск.

Основные шаги реконструкции
Сначала определяются сегменты проекций, в которые проецируется реконструируемый объем с учетом перспективы. На основании этих данных определяется, какие проекции нужны для реконструкции. Если в RAM-кэше имеются сегменты файлов, не входящие в этот список, то они удаляются из памяти.

Поток реконструкции обращается в кэш за сегментом проекции, блок памяти, содержащий проекцию (с учетом размера страницы 4096 байта) запирается в памяти, что запрещает ее выгрузку в своп, и указатель передается в CUDA-процедуру. Все дальнейшие действия происходят в памяти ускорителя. Происходит распаковка из 12 бит в float, далее все вычисления ведутся в float. При распаковке сегмент обрезается слева и справа до ширины реконструируемого блока плюс зазор, необходимый для свертки при фильтрации проекции. Происходят предварительные обработки: инверсия, гамма-коррекция, фильтрация усредненной проекцией, необходимое количество итераций сглаживания. Далее происходит свертка, и сегмент еще раз обрезается слева и справа до минимальной ширины, необходимой при обратном проецировании. Так обрабатываются проекции, пока хватает памяти на видеокарте. Т.е. на видеокарте формируется массив сегментов, готовых для обратного проецирования.

Суть обратного проецирования — просуммировать для каждого вокселя со всех проекций вес точки, с которой попадал луч источника рентгеновского излучения. Один вызов CUDA-ядра производит расчет по 32 вокселям, расположенным друг над другом. При этом делается цикл по всем загруженным в память сегментам проекций. Это позволяет хранить все промежуточные данные в регистрах и не делать промежуточных записей в память. По окончании расчетов в память записывается значение плотности вокселя. Ядро обратного проецирования имеет 2 реализации, одна медленная с проверками, что на проекции имеется точка, с которой брать данные, т.к. на концах проекций не всегда имеется точка, откуда берется значение. Быстрая реализация выполняет никаких проверок. Нужная реализация выбирается автоматически. Выборка значения из проекции производится по алгоритму «ближайшего соседа». Использование текстурной памяти на первых этапах показало резкое снижение производительности, а на данном этапе при использовании массивов проекций оказалось невозможным создание массивов текстур из-за ограничений CUDA 4.2.

Если памяти недостаточно, то для расчетов может потребоваться несколько итераций загрузки проекций и обратного проецирования.

По завершении расчетов делается оценка полученных вокселей. Считается максимальное и минимальное значение плотности, строится гистограмма. Построение гистограммы и копирование результатов в RAM производится параллельно.

При наличии нескольких CUDA устройств сегменты реконструируемого куба обрабатываются параллельно. По завершении реконструкции куба сжатием куба начинает заниматься другой поток, а поток реконструкции сразу принимается за следующее задание при условии достаточного количества оперативной памяти. Как оказалось, выделение и освобождение больших сегментов памяти — очень затратная по времени операция, по этому все полученные большие блоки памяти используются повторно. Так на CUDA делается выделение памяти под блок вокселей, несколько промежуточных буферов, а вся остальная память выделятся под проекции, и управление размещением проекций в ней выполняется уже вручную.

Сжатие
Сжатие в октодерево производится в несколько потоков. Количество потоков зависит от количества процессорных ядер. Каждый поток обрабатывает свой октант. Далее происходит сохранение в файл, который был указан клиентом реконструкции в задаче, и отправляется уведомление, что обработка кубика завершена.Клиент
Клиент ведет базу данных кубиков в виде файла SQLite. В нем сохраняются характеристики кубов, время реконструкции и т.д. По завершении реконструкции программа клиента закрывается, таким образом можно организовывать пакетные задачи на реконструкцию.Пример кода на CUDA
Ядро (measureModel.cu), которое делает первый проход при расчете гистограммы. Файл приведен, чтобы показать общий вид кода на CUDA в реальном рабочем проекте.

#include 
#include 
#include 
#include 

#include "CudaUtils.h"
#include "measureModel.h"

#define nullptr NULL

struct MinAndMaxValue
{
  float minValue;
  float maxValue;
};
__global__ void
cudaMeasureCubeKernel(float* src, MinAndMaxValue* dst, int ySize, int sliceSize, int blocksPerGridX)
{
  int x = blockDim.x * blockIdx.x + threadIdx.x;
  int z = blockDim.y * blockIdx.y + threadIdx.y;
  int indx = z * blocksPerGridX * blockDim.x + x;
  MinAndMaxValue v;
  v.minValue = src[indx];
  v.maxValue = v.minValue;
  //indx += sliceSize;
  for (int i = 0; i < ySize; ++i)
  {
    float val = src[indx];
    indx += sliceSize;
    if (v.minValue > val)
    v.minValue = val;
    if (v.maxValue < val)
    v.maxValue = val;
  }

  //помещаем данные по нашей строке в разделяемую память
  __shared__ MinAndMaxValue tmp[16][16];
  tmp[threadIdx.y][threadIdx.x] = v;
  //все нити нашего блока посчитали свои значения
  __syncthreads();

  if (threadIdx.y == 0)
  {//первой строкой потоков делаем свертывание временных данных до 16 значений
    for (int i = 0; i < blockDim.y; i++)
    {
      if (v.minValue > tmp[i][threadIdx.x].minValue)
      v.minValue = tmp[i][threadIdx.x].minValue;
      if (v.maxValue < tmp[i][threadIdx.x].maxValue)
      v.maxValue = tmp[i][threadIdx.x].maxValue;
    }
    tmp[0][threadIdx.x] = v;
  }
  __syncthreads();
  ///делаем сверку до одного значения
  if (threadIdx.x == 0 && threadIdx.y == 0)
  {
    for (int i = 0; i < blockDim.y; i++)
    {
      if (v.minValue > tmp[0][i].minValue)
      v.minValue = tmp[0][i].minValue;
      if (v.maxValue < tmp[0][i].maxValue)
        v.maxValue = tmp[0][i].maxValue;
    }
    dst[blockIdx.y * blocksPerGridX + blockIdx.x] = v;
  }
}

void Xrmt::Cuda::CudaMeasureCube(MeasureCubeParams ¶ms)
{
  //будем делать расчеты квадаратными блоками по 256 потока
  int threadsPerBlockX = 16;
  int threadsPerBlockZ = 16;
  int blocksPerGridX = (params.xSize + threadsPerBlockX - 1) / threadsPerBlockX;
  int blocksPerGridZ = (params.zSize + threadsPerBlockZ - 1) / threadsPerBlockZ;
  int blockCount = blocksPerGridX * blocksPerGridZ;
  dim3 threadDim(threadsPerBlockX, threadsPerBlockZ);
  //размер грида
  dim3 gridDim(blocksPerGridX, blocksPerGridZ);

  MinAndMaxValue *d_result = nullptr;
  size_t size = blockCount * sizeof(MinAndMaxValue);
  checkCudaErrors(cudaMalloc( (void**) &d_result, size));

  cudaMeasureCubeKernel<<>>(
    params.d_src,
    d_result,
    params.ySize,
    params.xSize * params.zSize,
    blocksPerGridX
  );

  checkCudaErrors(cudaDeviceSynchronize());

  MinAndMaxValue *result = new MinAndMaxValue[blockCount];
  checkCudaErrors(cudaMemcpy(result, d_result, size, cudaMemcpyDeviceToHost));

  params.maxValue = result[0].maxValue;
  params.minValue = result[0].minValue;
  for (int i = 1; i < blockCount; i++)
  {
    params.maxValue = std::max(params.maxValue, result[i].maxValue);
    params.minValue = std::min(params.minValue, result[i].minValue);
  }

  checkCudaErrors(cudaFree(d_result));
}

__global__ void
cudaCropDensityKernel(float* src, int xSize, int ySize, int sliceSize, float minDensity, float maxDensity)
{
  int x = blockDim.x * blockIdx.x + threadIdx.x;
  int z = blockDim.y * blockIdx.y + threadIdx.y;
  int indx = z * xSize + x;
  for (int i = 0; i < ySize; ++i)
  {
    float val = src[indx];
    if (val < minDensity)
    src[indx] = 0;
    else if (val > maxDensity)
    src[indx] = maxDensity;
    indx += sliceSize;
  }
}

void Xrmt::Cuda::CudaPostProcessCube(PostProcessCubeParams ¶ms)
{
  //будем делать расчеты квадаратными блоками по 256 потока
  int threadsPerBlockX = 16;
  int threadsPerBlockZ = 16;
  int blocksPerGridX = (params.xSize + threadsPerBlockX - 1) / threadsPerBlockX;
  int blocksPerGridZ = (params.zSize + threadsPerBlockZ - 1) / threadsPerBlockZ;
  dim3 threadDim(threadsPerBlockX, threadsPerBlockZ);
  //размер грида
  dim3 gridDim(blocksPerGridX, blocksPerGridZ);

  cudaCropDensityKernel<<>>(
    params.d_src,
    params.xSize,
    params.ySize,
    params.xSize * params.zSize,
    params.minDensity,
    params.maxDensity
  );

  checkCudaErrors(cudaDeviceSynchronize());
}

//на сколько частей делим единицу
#define DivideCount 8
#define ValuesPerThread 32
#define SplitCount 16
#define SplitCount2 64

__global__ void
cudaBuildGistogramKernel(
  float *src, 
  int count, 
  int *d_values,
  int minValue,
  int barCount
)
{
  //индекс значения, начиная с которого считаем
  int barFrom = threadIdx.x * ValuesPerThread;
  int blockIndx = SplitCount * blockIdx.x + threadIdx.y;
  int blockLen = count / (SplitCount * SplitCount2);

  unsigned int values[ValuesPerThread];
  for (int i = 0; i < ValuesPerThread; i++)
  {
    values[i] = 0;
  }

  src += blockLen * blockIndx;
  for(int i = blockLen - 1; i >= 0; i--)
  {
    float v = src[i];
    int indx = (int)((v - (float)minValue) * DivideCount) - barFrom;
    if (indx >= 0 && indx < ValuesPerThread)
      values[indx]++;
  }

  for (int i = 0; i < ValuesPerThread; i++)
  {
    d_values[blockIndx * barCount + barFrom + i] = values[i];
  }
}

__global__ void
cudaSumGistogramKernel(
  int *d_values,
  int barCount
)
{
  //индекс столбика, который суммируем
  int barIndx = blockIdx.x * ValuesPerThread + threadIdx.x;

  unsigned int sum = 0;
  d_values += barIndx;
  for (int i = 0 ; i < SplitCount * SplitCount2; i++)
  {
    sum += d_values[i * barCount];
  }

  d_values[0] = sum;
}

void Xrmt::Cuda::CudaBuildGistogram(BuildGistogramParams ¶ms)
{
  checkCudaErrors(cudaMemcpyAsync(
  params.h_dst, params.d_src, params.count * sizeof(float), cudaMemcpyDeviceToHost, 0
));

  //определяем минимальное значение в гистограмме
  int minValue = (int)(params.minDensity - 1);// для отрицательных значений отбрасывается дробная часть, а этого не достаточно!
  minValue = std::max(minValue, -200);
  //максимальное значение в гистограмме
  int maxValue = (int)params.maxDensity;
  maxValue = std::min(maxValue, 200);
  //количество столбиков в гистограмме (диапазон в 1 делим на DivideCount частей)
  int barCount = (maxValue - minValue + 1) * DivideCount;
  ///делаем количество столбиков кратным ValuesPerThread
  int x32 = barCount % ValuesPerThread;
  barCount += (x32 == 0) ? 0 : ValuesPerThread - x32;

  ///настройка потоков:
  /// x - каждый поток считает 32 столбика, т.е. x пропорционален ширине гистограммы
  /// y - делим блок данных на SplitCount частей
  dim3 threadDim(barCount / 32, SplitCount);
  ///размер грида, делим все данные на SplitCount2 частей
  dim3 gridDim(SplitCount2);
  ///таким образом все данные делим по блокам на SplitCount2 * SplitCount частей
  ///каждую такую часть будет обрабатывать barCount / 32 потоков

  ///резервируем память для хранения промежуточных результатов
  int *d_values = nullptr;
  ///для каждого блока свои значения
  size_t blockValuesCount = SplitCount2 * SplitCount * barCount;
  size_t d_size = blockValuesCount * sizeof(int);
  checkCudaErrors(cudaMalloc( (void**) &d_values, d_size));

  ///выполняем обработку по блокам
  cudaBuildGistogramKernel<<>>(
    params.d_src,
    params.count,
    d_values,
    minValue,
    barCount
  );
  //суммируем блоки на GPU
  cudaSumGistogramKernel<<>>(
    d_values,
    barCount
  );
  checkCudaErrors(cudaDeviceSynchronize());
  //получаем значения гистограммы
  params.histogramValues.resize(barCount);
  checkCudaErrors(cudaMemcpy(
    ¶ms.histogramValues[0], 
    d_values, 
    barCount * sizeof(int), 
    cudaMemcpyDeviceToHost
  ));
  checkCudaErrors(cudaFree(d_values)); 
  params.histogramStep = 1.0 / DivideCount;
  params.histogramStart = (float)minValue;
}

Вопрос №2

Камера, которую вы использовали (PIXIS-XF, надо полагать), отдаёт картинки 2048×2048, а в статье вы пишете «до 8000×8000». Это вы как получили? Вы перемещаете также образец или камеру по вертикали и горизонтали и склеиваете потом картинки? AndreyDmitriev

Да, в микро томографе использовалась камера PIXIS-XF:2048B. Размер реконструкции по ТЗ 8000×8000x20000, по ширине и глубине 8000 означает, что камера видит только часть изображения, но реконструируется больше, это дает падение качества реконструкции по краям. По высоте просто перемещается столик, делается новая реконструкция, и результаты склеиваются.

Вопрос №3

Демо-изображения, которые в видео в конце статьи, все получены из 360 проекций? Если так, то это хорошо, ведь 360 проекций с шагом в градус — довольно мало, обычно идут с шагом треть/четверть градуса, иначе будут артефакты реконструкции. Вроде есть формула оптимального количества проекций для заданного разрешения, но вот запамятовал. AndreyDmitriev

В нашем случае использовалось 180–360 проекций. Различные алгоритмы могут давать разное качество реконструкций в зависимости от количества проекций, но в общем случае выполняется правило, что с увеличением количества проекций качество возрастает. Для наших задач было достаточно использовать 180–360 проекций для получения хорошего качества.

Алгоритм нормально реагирует на пропуски кадров ценой небольшого снижения разрешения в направлении, где есть пропуски. Кроме того, камера имела особенность перегреваться, и у нее плавала «яркость», поэтому часть кадров отбрасывалась как бракованные, остальные нормализовались по средней яркости.

Вопрос №4

Ещё я не очень понял про частоту камеры. По спецификации она двухчастотная на 100 килогерц или два мегагерца. Если у неё четыре мегапиксела, это значит, что она отдаёт кадр каждые две секунды на максимальной частоте? AndreyDmitriev

Да, вы правы.
Согласно документации камеры, характеристики частоты следующие: ADC speed/bits 100 kHz/16-bit and 2 MHz/16-bit

То, есть если одна точка изображения имеет разрядность 16 бит, то получаем, что частота для всего изображения будет: 2000000 / (2048×2048) = 0,47 герц

Вопрос №5

Вы перемещаете манипулятор пошагово или непрерывно? Сколько времени занимает сканирование типичных образцов, что представлены на видео? AndreyDmitriev

Манипулятор (столик) передвигается шагово. Повернули на угол, остановили, отсняли, снова повернули и т.д.
Среднее время сканирования — 11 минут на 378 кадров.

Вопрос №6

Ну и про 12 бит — очень любопытно. То, что отрезать четыре бита и упаковать каждые два пиксела в три байта можно для хранения и передачи — это понятно. Но для реконструирования вам же придётся снова развернуть каждый пиксел как минимум в два байта? Или у вас вся математика на 12-ти битах? В таком случае как вы решили проблему того, что пикселы занимают полтора байта и не выравниваются на границу? AndreyDmitriev

Формат файлов 12 битных боковых проекций.

1. Пиксели побитно упакованы и располагаются в строки, так что две точки занимают 3 байта, при этом предполагается, что ширина изображения проекции кратна 2, согласно формуле: lineWidthInBytes = width () * 3 / 2.
2. Обычно сразу весь объем данных не загружается, а используются «окна», в которые подгружается только необходимая порция изображения, при этом предполагается выравнивание левой и правой границ кратно четырем пикселям.
3. После загрузки «окна» дальнейшая работа ведется с помощью функций полного импорта/экспорта этого окна в массивы типа float, либо quint16. В процессе импорта/экспорта и происходит преобразование из 12 бит в нужную разрядность.
4. В нашем случае выигрыш от сокращения размеров файлов проекций был больше, чем потеря производительности при этом. Кроме того, так как загружались файлы не полностью, а только «окна», предназначенные для обработки на конкретной машине кластера, то потери производительности еще меньше за счет распараллеливания задач.

Объемный (воксельный) рендеринг в реальном времени

Так же интересной задачей было отображение модели с использованием вокселей в реальном времени. Помимо вокселей самой модели нужно было отображать в 3D такие инструменты, как ограничивающий параллелепипед, секущую плоскость, скрывать половину объекта вдоль секущей плоскости, а также скрывать объект за пределами параллелепипеда. На секущей плоскости отображается элемент интерфейса пользователя в виде «рычажка» (который в то же время соответствует вектору нормали), позволяющего перемещать окно среза проекции по секущей плоскости и саму плоскость смещать вдоль вектора нормали. Окно среза проекции можно так же растягивать за его границы и вращать. На ограничивающем параллелепипеде помимо его ребер отображаются такие же «рычажки» как на плоскости, которые так же позволяют изменять его размеры. Все эти манипуляции выполняются в реальном времени и объеме пространства модели.

Достаточная частота кадров при работе обеспечивалась за счет динамического уровня детализации, так как подгрузка данных происходит при уменьшении ограничивающего прямоугольника автоматически.

Для манипуляций элементами интерфейса в 3D были реализованы специальные наборы математических функций. Первоначальное создание секущей плоскости если описать его в общих понятиях без использования формул, выглядит примерно так: пользователь дважды щелкает мышкой в любую точку модели, после чего эта точка фиксируется, и из нее при дальнейшем движении мышью отображается вектор нормали к создаваемой плоскости. При этом фактически плоскость уже создана, и она лежит на луче, идущем из экранных координат курсора мыши вглубь пространства, не параллельно линиям перспективы, так что луч проецируется, как точка на экран, и ориентация плоскости меняется при перемещении мыши динамически, и пользователь видит это сразу на экране. Для завершения создания нужно еще раз щелкнуть мышкой, чтобы зафиксировать ориентацию плоскости.

Кроме элементов манипуляции моделью в объеме есть инструменты для управления цветовыми спектрами плотностей и уровнями прозрачности.

Непосредственно сам рендеринг вокселей и обрезка секущей плоскостью и ограничивающим параллелепипедом были реализованы с помощью библиотеки VTK.

Список математических функций

Математические классы и функции, используемые для геометрических вычислений в проекте.
1. Класс плоскости.

• Описание плоскости по нормали и точке.
• Описание по трем точкам.
• Угол поворота 2D-системы координат внутри плоскости вокруг вектора нормали.
• Отступы границ 2D- прямоугольной области внутри плоскости с точкой отсчета на векторе нормали.
• Функции перехода от 2D-точки внутри плоскости повернутой вокруг нормали к реальным 3D-координатам и обратное преобразование.

2. Набор математических функций для геометрических вычислений.
3. Математические функции, используемые при реконструкции.

Больше проектов:
Как за 5233 человеко-часа создать софт для микротомографа
SDK для внедрения поддержки электронных книг в формате FB2
«Сфера»: как мониторить миллиарды киловатт-часов
Управление доступом к электронным документам. От DefView до Vivaldi
Разработка простого плагина для JIRA для работы с базой данных
В помощь DevOps: сборщик прошивок для сетевых устройств на Debian за 1008 часов
Автообновление службы Windows через AWS для бедных

© Habrahabr.ru