Почему существует только 5 правильных многогранников? Ответ даёт неравенство из 8-го класса
Давайте сегодня поговорим про платоновы тела, которые представляют из себя правильные многогранники. Еще со времен Древней Греции было известно, что их всего лишь пять:

«Шизофрения», творящаяся на картинке выше, обусловлена представлениями древнегреческих философов, согласно которым существует пять основных элементов, из которых состоит мир: земля, вода, воздух, огонь и эфир.
Платон установил соответствие между этими пятью элементами и пятью правильными многогранниками (платоновыми телами):
Земля — куб (шестигранник) — наиболее устойчивое и неподвижное тело.
Вода — икосаэдр (двадцатигранник) — подвижная и неустойчивая форма.
Воздух — октаэдр (восьмигранник) — легкое и подвижное тело.
Огонь — тетраэдр (четырехгранник) — острое и колющее тело.
Эфир — додекаэдр (двенадцатигранник) — тело, наиболее близкое к шару, символизирующее небесную сферу.
Другой древнегреческий ученый Теэтэт Афинский доказал, что этот список правильных многогранников — исчерпывающий. Об этом писал Евклид в своих «Началах» в 13 книге:

Однако, более интересным с моей точки зрения является топологически-алгебраическое доказательство этого замечательного факта. Для его понимания не понадобится, в принципе, никаких дополнительных знаний за исключений формулы Эйлера и особого классификатора многогранников — нотации Шлефли.
Символы Шлефли
Задача классификация правильных многогранников в целом различных размерностей — одна из важных задач геометрии, которую проще всего оказалось решить комбинаторными средствами.
Людвиг Шлефли (1814–1895) — швейцарский математик, специалист в области многомерной геометрии и комплексного анализа. Преподавал в Бернском университете
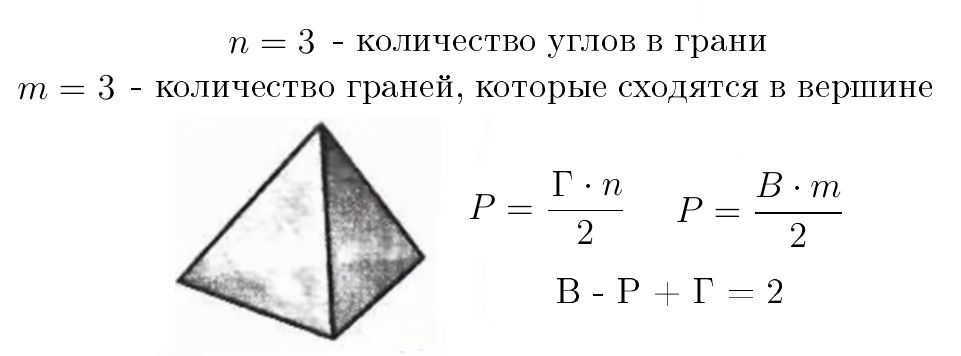
В своей диссертации Шлефли дал полную классификацию правильных многогранников для n-размерных пространств. С тех пор в научный оборот вошел т.н. символ Шлефли {n, m}, где n — количество углов в грани, m — количество граней, которые сходятся в вершине.
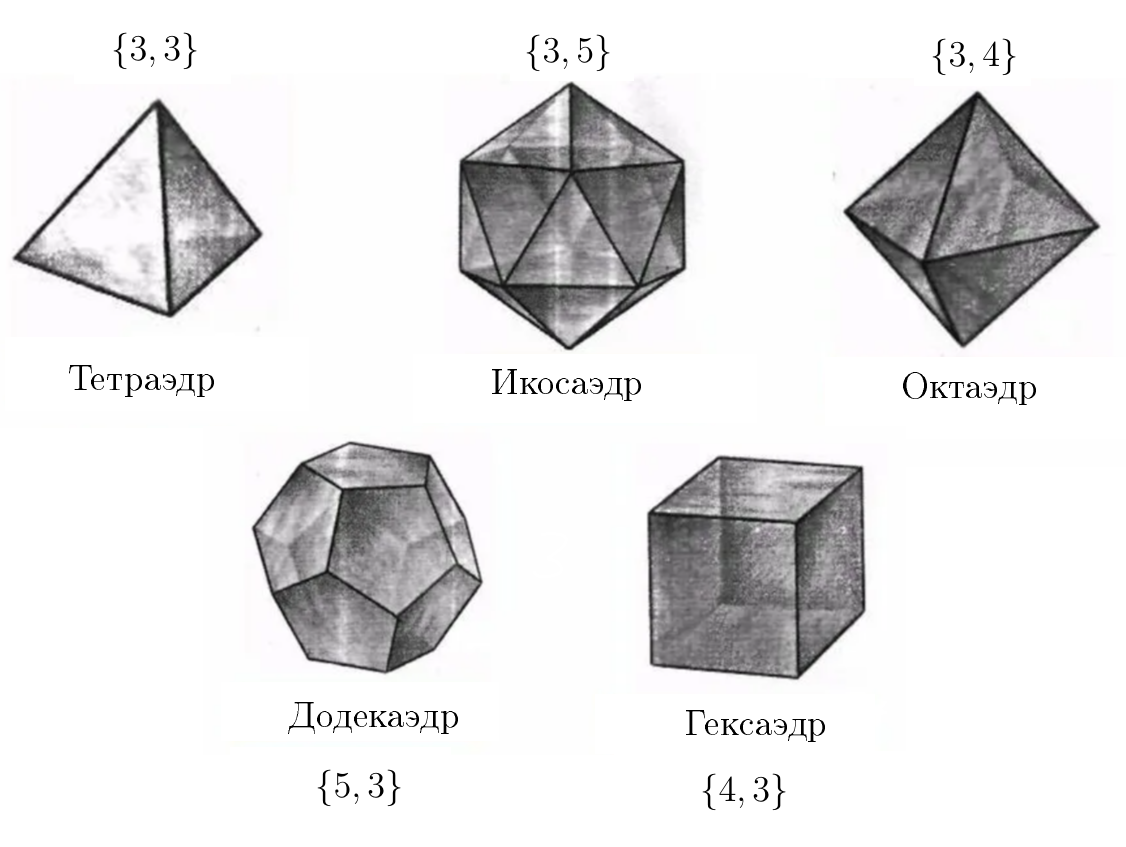
Додекаэдр — это правильный многогранник, имеющий по 3 пятиугольника вокруг каждой вершины. И да, куб — это гексаэдр в том смысле, что у него восемь вершин.
Нотация Шлефли простирается и за пределы третьего измерения. Например, символом {4,3,3} обозначается тессеракт (гиперкуб). Он имеет по три куба {4,3} у каждого ребра.
Запомните эти символы. Они встретятся нам в конце повествования. Переходим к следующему инструменту.
Великая формула Эйлера
Одно из самых известных открытий великого математика — это формула, которая связывает количество вершин, ребер и граней всякого многогранника, топологически эквивалентного сфере:

Обратите внимание, что речь идёт не только о правильных многогранниках, а вообще о всех телах, которые можно получить непрерывными преобразованиями из сферы (т.е. гомеоморфными ей). Эйлерова характеристика, т.о. — это топологический инвариант.

Знаменитая картинка, которая показывает, что бублик и кружка — суть одно и тоже
Для топологических пространств эйлерова характеристика имеет немного другой вид: χ = 2 — 2g, где g — количество «ручек». Тор можно получить «приклеив» к сфере одну ручку, значит его Эйлерова характеристика равна 0, если приклеить две ручки — получим двойной тор с характеристикой »-2»:

Подводя краткие итоги: мы будем классифицировать правильные двумерные многогранники (двумерные — в смысле, что их поверхность двумерна, но вложены они всё-таки в трехмерное пространство). Их эйлерова характеристика равна 2.
Классификация двумерных полиэдров
Наша задача состоит в том, чтобы связать символы Шлефли {n, m} с количеством вершин, ребер и граней. Для примера рассмотрим тетраэдр и попытаемся выяснить зависимость.
У тетраэдра 4 грани, в каждой из которых три угла. Т.о., если умножить 4 грани на 3 угла получим 12 чего-то там, что в два раза больше, чем количество его ребер (каждое из них посчитано дважды).
В каждой вершине сходятся m=3 граней. Если умножить 4 вершины на 3 грани получим 12 чего-то там, что в два раза больше количества ребер (их так же считали дважды
В качестве упражнения можно посчитать для куба. В каждой из 6 граней 4 угла, отсюда (6×4)/2 = 12 ребер. В каждой из 8 вершин сходятся 3 грани, что даёт (8×3)/2 = 12 ребер.
Получили три уравнения с тремя неизвестными, которые будем сейчас решать, чтобы получить в чистом виде зависимость от составляющих символа Шлефли:

Такую систему уравнений удобно решить, воспользовавшись параметризацией через некое t. Во второй строчке подставили данные в уравнение Эйлера и затем привели дроби к одному знаменателю
Из очевидных соображений, что t > 0, мы должны потребовать положительности знаменателя. Остается в целых числах решить соответствующее неравенство:

Не только лишь все натуральные числа при умножении дают результат, меньший 4, поэтому у нас не так много работы:

А теперь вспомните рисунок с символами Шлефли для платоновых тел! Как видите, мы получили одно и то же с помощью решения обычной системы уравнений! Алгебраизация — один из самых мощных способов исследования окружающего нас мира.
P.S. Морфоэдр
Эта фигура которая состоит из последовательно вложенных друг в друга платоновых тел.
Пораженный концепцией такого изысканного тела, великий астроном Иоганн Кеплер предположил, что расстояния между известными тогда (стык 15 и 17 веков) шести планетами — Меркурием, Венерой, Землей, Марсом, Юпитером и Сатурном выражаются через размеры пяти правильных выпуклых многогранников.
Между каждой парой небесных сфер, по которым, согласно его гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел, в результате чего получилась композиция, которая известна в науке как «Космический кубок Кеплера»:

Спасибо за внимание, и пусть ваш земной кубок будет более простым!
Много интересного — в Telegram «Математика не для всех»
