Почему не нужно сваливать на неточность O-оценок свои проблемы

На написание данного поста меня подвигла недавняя публикация этого и вот этого переводов, в которых авторы в интеллигентной форме выражают свое недовольство по поводу того, как O-оценки вычислительной сложности классических, казалось бы, алгоритмов вступили в диссонанс с их практическим опытом разработки. Основным предметом критики послужила модель памяти, в рамках которой эти оценки были получены — она, де, не учитывает особенности иерархической организации по принципу быстродействия, которая имеет место быть в современных вычислительных системах. От чего и произрастают все последующие неприятности. И судя по наблюдаемой реакции благодарных читателей, авторы далеко не одиноки в своем негодовании и желании «наехать» на классиков с их О-большими. Так возможно, действительно стоит отправить на свалку истории выкладки дядек в белых халатах, сделанные ими для ламповых тугодумающих и пышащих жаром машин, и дать дорогу молодым амбициозным моделям, более точно отражающим анатомию современного «железа»?
Давайте разбираться
По ходу текста я буду ссылаться на вторую публикацию и некоторые комментарии к ней. Тронуло за живое. Но для начала давайте точно условимся что под чем понимается по ходу данного текста.
Введем определение. Пусть и
— две вещественные функции, определенные на множестве
. Тогда из
следует, что найдется такое положительное число
, что для всех
справедливо
. Такое обозначение называют
-нотацией, а O называют символом Бахмана, либо просто »О-большим».
Из этого определения сразу имеется несколько следствий:
1. Если для всех имеет место
, то из
» следует, что
. В частности, имеем, что умножение на константу не меняет O-оценку.
Проще говоря, при умножении O-выражения на константу символ Бахмана эту константу «съедает». Это означает, что знак равенства в выражении, включающем в себя O-оценку, нельзя интерпретировать как классическое «равенство» значений и к таким выражениям нельзя применять математические операции без дополнительных уточнений. В противном случае мы бы получили странные вещи по типу следующей: . Это следствие произвольности константы, которая «прячется» за символом Бахмана.
2. Если ограничена на
, то есть существует такое число
, что для всех
выполняется
, то
.
Переводя с математического на русский и взяв для простоты в качестве конечный интервал числовой прямой, имеем следующее: если функция на заданном интервале не уходит в бесконечность, то самое бессмысленное, что можно о ней еще сказать — это то, что ей соответствует O(1). Это совершенно ничего нового не говорит о ее поведении.
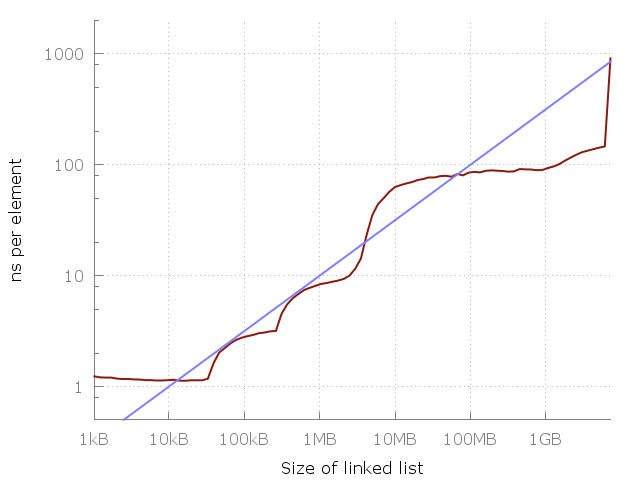
Голубая линия это O (√N).
Вернемся к случаю оценки сложности алгоритма и посмотрим на картинку, приводимую автором цитируемой публикации. Наблюдая рост времени выполнения, делается вывод о несостоятельности оценки O (1). Но интервал, на котором анализируется поведение программы, конечен. Значит по факту утверждается, что оценка O (1) на нем плоха.
Чтож… спасибо, Кэп.
Более того, дальше делается попытка угадать! мажорирующую функцию просто по виду кривой, дескать, «гля как похоже». Не проводя никакого анализа самого алгоритма с учетом тех особенностей, на которых пытаются акцентировать внимание и не вводя никакой модели памяти! А почему, собственно, там корень квадратный, а не кубический? Или не логарифм какой-нибудь залетный? Ну, право слово, предложили бы хоть пару-тройку вариантов, зачем же сразу «внимание, правильный ответ»?
Здесь стоит оговориться. Я, естественно, не веду к неверности выводов о том, что при переходе к «более далекому» от процессора накопителю время доступа падает. Но время получения порции данных при произвольном доступе к памяти даже на самом медленном уровне иерархии есть величина постоянная или хотя бы ограниченная. Из чего и следует оценка O (1). А если она не ограниченная и зависит от размерности данных — значит доступ к памяти не произвольный. Ну тупо по определению. Давайте не забывать, что мы имеет дело с идеализированными алгоритмическими конструкциями. Поэтому когда говорится, что «дальше за HDD пойдут датацентры»… Господа, ну какой же это произвольный доступ, какие массивы и хэш-таблицы? Это называется мухлёж под столом: вы втихаря меняете условия задачи, приводите ответ к предыдущей и кричите: «Ахтунг! Неправильно-то как!». У меня это вызывает приступ тяжелого недоумения. Ведь если за словом array, vector или <какой-то-тип>* ваш компилятор скрывает, скажем, кусок распределенной по узлам кластера памяти — то это по структуре может быть что угодно, но не массив в терминах книг Вирта и Кнута, и применять к ним написанные в этих книгах результаты формального анализа в высшей степени бестолковая идея. И не меньшая шизофрения — на полном серьезе говорить об общности оценки, придуманной глядя на график с результатами произвольного теста.
Ошибочность приводимого суждения заключается в том, что O-оценка сложности делается на основании эксперимента. Чтобы это подчеркнуть, введем еще одно «свойство» O-нотации, применимое к оценкам алгоритмической сложности:
3. O-оценка может быть получена только из анализа структуры алгоритма, но не из результатов эксперимента. По результатам эксперимента можно получить статистические оценки, экспертные оценки, прикидочные оценки и, наконец, инженерное и эстетическое удовольствие —, но не асимптотические оценки.
Последнее является следствием того, что сам смысл подобных оценок — это получить представление о поведении алгоритма при достаточно больших размерностях данных, причем насколько больших обычно не уточняется. Это не единственная и далеко не всегда главная, но представляющая интерес характеристика алгоритма. Во времена Дейкстры и Хоара достаточно большими можно было считать порядки размерности 3–6, в наше время 10–100 (по моим не претендующим на глубину анализа оценкам). Иными словами, ставя вопрос о получении асимптотических оценок функции сложности алгоритма, удобно модифицировать определение O-нотации таким образом:
Пусть . Тогда
означает, что существуют взаимно независимые положительные числа A и n, такие что для всех
выполняется
.
То есть при анализе алгоритмической сложности мы фактически рассматриваем мажоранты функции сложности на всех ограниченных слева и не ограниченных справа интервалах. Значит таких О-оценок может быть указано сколь угодно много и все такие оценки могут оказаться практически полезными. Некоторые из них будут точными для малых N, но быстро уходить в бесконечность. Другие будут расти медленно, но станут справедливы начиная с такого N, до которого нам на наших убогих компьютерах как пешком до Луны. Так что если допустить, что за оценкой времени доступа к памяти скрыт какой-либо структурный анализ, то эту оценку вполне можно было бы использовать в определенном диапазоне размерностей, но даже тогда она бы не отменила верность оценки O (1).
Классический пример некорректного сравнения асимптотических оценок — алгоритмы умножения квадратных матриц. Если делать выбор между алгоритмами только на основании сравнения оценок, то берем алгоритм Уильямс и не паримся. Можно лишь пожелать творческих успехов решившему применить его к матрицам характерных для инженерных задач размерностей. Но с другой стороны, мы знаем, что начиная с некоторой размерности задачи алгоритм Штрассена и различные его модификации будут работать быстрее тривиального, и это дает нам пространство для маневра при выборе подходов к решению задачи.
Как из умности получаются глупости.
Грешить на неточность O-оценок — значит полностью не понимать смысл этих оценок, и если это так — то никто не заставляет их использовать. Вполне можно и зачастую оправдано предпочитать им статистические оценки, полученные в результате тестов на специфических именно для вашей области наборах данных. Неграмотное использование такого тонкого инструмента, как асимптотический анализ, приводит к перегибам и вообще удивительным штукам. Например, используя O-нотацию, можно »«доказать»« несостоятельность идеи параллельного программирования.
Допустим, что наш алгоритм, которому скармливается порция данных размерности N и который при последовательном выполнении имеет сложность , легко и непринужденно разбивается на те же N независимых и для простоты одинаковых по вычислительной и временной сложности частей. Получаем, что сложность каждой такой части есть
. Пусть у нас есть M независимых вычислителей. Тогда общая сложность выполнения параллельного алгоритма есть ничто иное как
. Получилось, что асимптотическая оценка сложности алгоритма в результате даже идеальной параллелизации на конечное число процессов не меняется. Но внимательный читатель заметил, что изменилась «спрятанная» константа, которую схомячил символ Бахмана. То есть делать из подобного анализа какие-то общие выводы относительно самой идеи параллелизации по меньшей мере глупо. Но возможна и другая крайность — забыть, что количество процессоров конечно и на основании бесконечного ресурса параллелизма утверждать, что оценка «параллельной версии алгоритма» есть O(1).
Подведем итоги.
В качестве вывода можно предоставить следующие подкупающие новизной утверждения:
- Нельзя утверждать, что один алгоритм эффективнее другого на основании простого сопоставления их O-оценок. Такое утверждение всегда требует пояснений.
- Нельзя из результатов замеров производительности делать вывод о правильности или неправильности таких оценок — спрятанная константа обычно неизвестна и может быть достаточно большой.
- Можно (а иногда нужно) рассуждать об алгоритмах и структурах данных вообще не используя такие оценки. Для этого достаточно просто сказать, какие конкретно их свойства вас интересуют.
- Но лучше все-таки принимать конкретные инженерные решения, учитывая в том числе и такие характеристики употребляемых алгоритмов.
За утверждением о неточности, неправильности или непрактичности асимптотических оценок часто скрыто нежелание провести нормальный предварительный анализ поставленной проблемы и попытка опираться на название, но не суть тех абстракций, с которыми имеют дело. Говоря об асимптотической сложности алгоритма, грамотный специалист понимает, что речь идет об идеализированных конструкциях, держит в уме степень корректности проецирования их на реальное «железо» и никогда, от слова «вообще», не принимает инженерных решений опираясь только и исключительно на нее. O-оценки более полезны при разработке новых алгоритмов и поиске принципиальных решений сложных задач и намного менее полезны при написании и отладке конкретных программ под конкретное железо. Но если вы их неправильно интерпретировали и получили совсем не то, что обещало вам ваше понимание прочитанного в умных книжках — согласитесь, это не проблема тех, кто эти оценки доказательно получил.
Комментарии (4)
15 сентября 2016 в 04:38
0↑
↓
Ну да, в умных книжках абстракный исполнитель в вакууме, а не реальное железо. И для него эти оценки работают. Но смысла от них как от машины тьюринга — одна теория. На практике необходима другая система оценки, оценивающая современную архитектуру. И понимание O большого никак не отменяет необходимости ввести другую систему оценки. Тоже теоретической, тоже модельной, но уже заточенной под наше железо.Ваше предложение оценивать производительность алгоритмов постфактум, тестами — порочно. Откуда вы будете знать какие вообще алгоритмы реализовывать, чтобы потестить?
15 сентября 2016 в 05:02
+2↑
↓
Для написания программ под x86 пользы от машины Тьюринга и впрямь никакой, она не для этого и делалась. А вот для доказательства алгоритмической неразрешимости некоторых задач она очень даже кстати, а сие телодвижение позволит при попадании на такого рода задачу не биться головой об стену в поисках решения, а направить свои ментальные усилия в направлении поиска других подходов к вставшей инженерной проблеме.Ваше замечание ровно о том, что я написал в конце. Вы хотите иметь не математический инструмент, а дельфийского оракула: Вы к нему с задачей — он Вам алгоритм, ну или хотя бы «посмотри сюда, сравни это — и будет тебе счастье», как в справочнике слесаря-сантехника. Не бывает так, нет здесь серебряной пули и нормальный теоретический анализ алгоритма требует подходить к нему больше, чем с одного бока. Не можете провести такой анализ — используйте экспериментальные методы исследования. Не можете или не хотите делать ни того, ни другого — пользуйтесь эмпирическими рекомендациями в руководствах по языкам программирования. Можете выполнить и то, и другое — вообще золотой специалист.
15 сентября 2016 в 05:49 (комментарий был изменён)
0↑
↓
Вы ошибаетесь, я разумеется, хочу иметь инструмент, а не волшебную палочку. Математический инструмент, в рамках которого удобно обсуждать производительность программы. Такой показатель, который позволяет классифицировать производительность алгоритмов, который легко вычислить для простого алгоритма, и к которому легко редуцировать составленный из более простых алгоритмов.> Для написания программ под x86 пользы от машины Тьюринга и впрямь никакой, она не для этого и делалась. А вот для доказательства алгоритмической неразрешимости некоторых задач она очень даже кстати,
А вы не задумывались, зачем появилась в информатике О-большая нотация, когда уже была абстракция машины Тьюринга? Ведь последнего достаточно для рассуждений о вычислимости? Как оказалось, абстракция машины Тьюринга совершенно не подходит для оценки производительности алгоритмов на актуальном железе. И вот ввели новый инструмент, чисто для того, чтобы найти адекватный способ измерения производительности, подходящий для реального железа того периода.
Время идёт, новое железо уже совсем не похоже на старое. Понемногу, в деталях, оно трансформировалось в нечто, нарушающее все принципы машины фон-Неймана. Пора, соответственно, и математический аппарат подтянуть. Добавить новую, актуальную абстракцию. А старую модель оставить истории и теории, там же, где сейчас находится машина Тьюринга. Кстати, последнее время тьюринг-полноту принято показывать не приведением к оригинальной машине, а вычислением rule 110.
И задача теоретиков от computer science предоставить для практиков новую абстракцию, удобную к современному применению. Вы ведь не называете жалкими недоучками тех программистов, которые опираются (опирались когда это было актуально) на классические алгоритмы и их оценки?
15 сентября 2016 в 06:31 (комментарий был изменён)
0↑
↓
То, что Вы описали как раз вполне соответствует описанию волшебной палочки. Вы хотите иметь возможность запросто получать простые ответы на сложные вопросы.Так получилось, что я эти вопросы знаю. Машина Тьюринга в принципе не предназначена для ответа на вопросы о вычислительной сложности, она предназначалась для получения строгого ответа на вопросы «что есть алгоритм?» и какой «класс задач можно решить чисто механически?». О-нотация появилась совсем не в связи с алгоритмами, а с изучением введенных Пуанкаре асимптотических рядов. Просто так получилось, что при анализе вычислительной сложности эта нотация обычно оказывается достаточно удобной. Она позволяет упростить анализ, исключая по мере надобности лишние множители. Это вообще никак не связано с реальным железом, только лишь с удобством вычислений. Так что не надо валить все в кучу.
Машины Тьюринга и архитектура фон Неймана вещи мало связанные и нарушение принципов второй никак не сказывается на первой. Чем стара эта модель, тем что не удовлетворяет вашим потребностям как специалиста-практика? Еще раз повторюсь, ее не для того придумывали. И свою историческую задачу она, вообще говоря выполнила. Для ответа на другие вопросы придумывались другие модели и приемы.Но вы пытаетесь перевернуть все с ног на голову, ставя вопрос так, что вам нужен новый метод оценки старых алгоритмов. В самом основании этих «старых» алгоритмов лежали базовые упрощения действительности типа линейной модели памяти, и анализ их асимптотического поведения шел рука об руку с процессом их формулировки. Этот процесс не работает так, что вот мы что-то придумали — и давай его анализировать методами асимптотического анализа. Вас не устраивает, как старые алгоритмы ложатся на новое железо? Так садитесь и придумывайте новые. Но зачем же ставить CS-никам не свойственные им задачи потому, что такая их формулировка кажется Вам правильной?
