Почему мы трансформируем трёхмерные векторы матрицами 4х4?
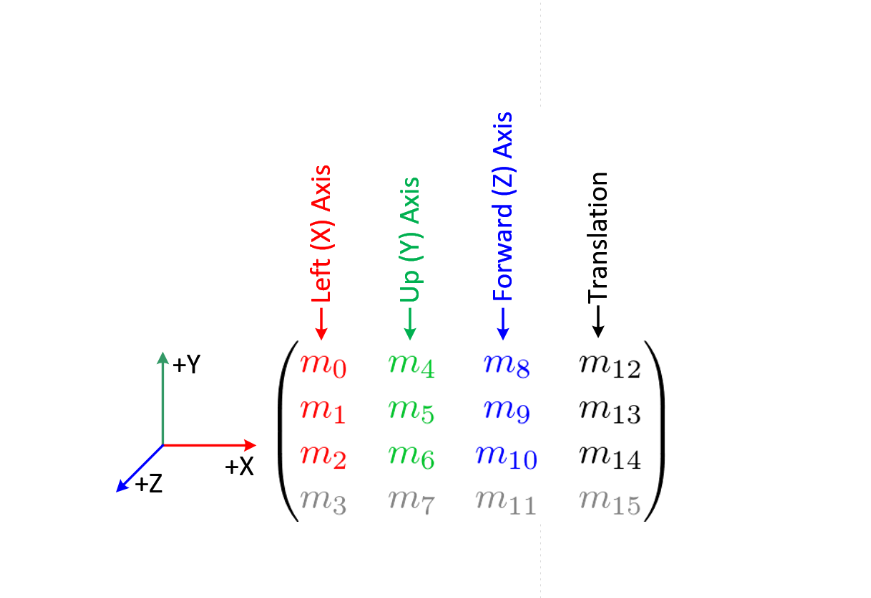
Почему не матрица 3×3? Почему в матрице 4×4 всё уложено именно так? Зачем там последняя строка, заполненная нулями и одной единицей в конце? Этими вопросами я задался накануне, решил поисследовать вопрос и рассказываю что выяснил.
В статье нас будут интересовать только афинные преобразования, а в частности вращение, масштабирование и перемещение, которые активно используются в программировании графики и разработке игр в целом.
Афинное преобразование является композицией двух функций: линейной и нелинейной трансформаций. Через линейные реализуются вращение и масштабирование, а сама трансформация задается матрицей той же размерности, что и пространство, в котором она применяется (A⋅x). Через нелинейные реализуются перемещения, но из свойства таковы, что такие трансформации не могут быть выражены матрицей, зато легко могут быть выражены слагаемым вектором (+b).
Афинное преобразование T, примененное на вектор x можно записать как
Трансформации одномерного вектора
Благодаря одномерности для простоты мы можем представить одномерную матрицу А, вектор b и вектор x как числа на вещественной прямой. Так же трансформированное значение x предпочту записывать как x', мне кажется так выглядит чуть более чисто:
![\begin{array}{ll} A\rightarrow [a] \rightarrow a, \\ \vec{b} \rightarrow (b) \rightarrow b, \\ \vec{x} \rightarrow x, \\ T(x) \rightarrow x' \end{array}](https://habrastorage.org/getpro/habr/upload_files/6db/081/881/6db081881bca3397f47a1bfc98fd5239.svg)
Итого
Через манипуляции с а мы можем растягивать или сжимать вектор x (линейно трансформировать), а через манипуляции с b перемещать (нелинейно трансформировать).
Случаи, когда используются обе, линейная и нелинейная трансформации вместе довольно частые. Было бы удобно найти такое одно преобразование M, чтобы выразить в нём сразу оба:
Возьмём для примера трансформацию x' = 3x + 4 (3x линейная трансформация и +4 нелинейная трансформация) и попробуем подобрать нужную матрицу.
Свойства линейных трансформаций таковы, что они могут быть выражены через матрицы (например преобразование 3x может быть выражено через одномерную матрицу [3]), однако нелинейные трансформации (x+4) таких свойств лишены, от чего не удается выразить M без зависимости от x.
Трюк: поднимается на размерность выше
Если представить +4 как +4y, введя дополнительную координату y, выразив её так же через x и саму себя, то получится система линейных уравнений
которую можно выразить через матрицу 2×2, которая в свою очередь может выразить x' = 3x+4 и при этом не будет зависеть от x, т.е будет линейной трансформацией. Нижнюю строку я не заполнил конкретными числами, потому что на данный момент они не важны.
Так как матрица 2×2 умножается только на двумерный вектор, то необходимо предоставить не только х, но и вторую координату — y, а так как она участвует в выражении +4y и мы хотим, чтобы это превратилось просто в +4, то вместе с неизвестным x на умножение с матрицей передаем единицу:
Второе выражение в системе нам не интересно, оно введено только для того, чтобы иметь возможность получить матрицу, однако в результате вычислений будет возвращен двумерный вектор, с 3x+4 для x' и чем-то для y' и было бы сподручнее получить единицу в y' вместо непонятно чего, ведь в таком случае мы получим удобный вектор
который будет удобно умножать на любую другую матрицу далее. Чтобы получить единицу заполняем выражение соответствующими коэффициентами: y' = 1 = 0 ⋅ x + 1 ⋅ 1
Вот так у нас получается матрица, которая может быть выражена независимо от x и способна выполнять афинные трансформации над одномерными векторами, заключенными в двумерные.
Получается в матрице заключена линейная трансформация (a), нелинейная трансформация (b) и служебная строка (0 1) которая сохраняет для y' значение 1, чтобы вычисления x' проходили так, как мы ожидаем.
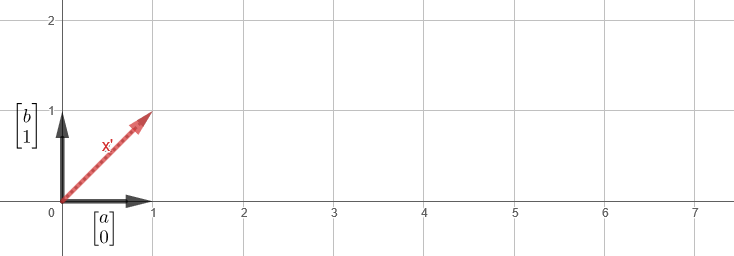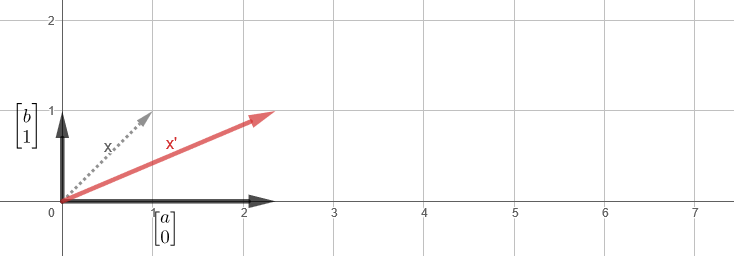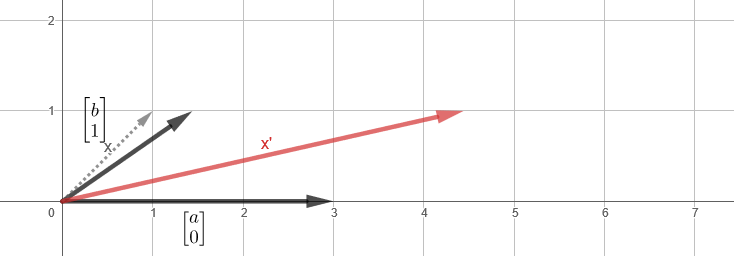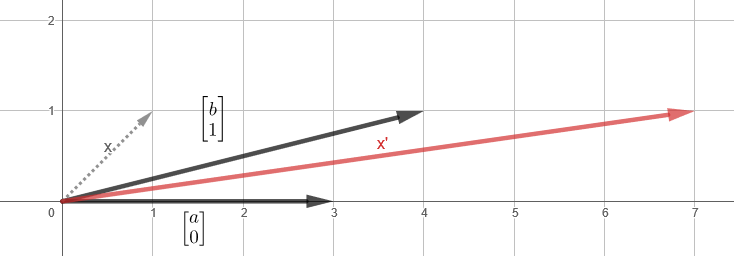
На самом деле трансформация — это просто хитрое слово, обозначающее функцию, но предполагающая отображение некоторого движения. Вот как трансформация из примера выглядит визуально (ссылка):
Тот же трюк, но в двумерном пространстве
Имеем матрицу для вращения или масштабирования и вектор для перемещения
Чтобы иметь возможность задать матрицей оба преобразования поднимается на размерность выше и выполняет принципиально те же действия, что в одномерном случае, только теперь новая компонента — это z, потому что y уже существует и нужна.
Матрица линейной трансформации выросла до 2×2 по понятным причинам двумерности пространства. Вектор b тоже вырос до двумерного и способен перемещать по обеим осям.
Вычисляемые значения для x' и y' будут такими же, как если бы мы считали по отдельности каждую трансформацию, а z' всегда будет равен 1 для удобства.
В трёхмерном пространстве ничего нового
Два преобразования, одно (линейное) выражено через матрицу, а другое (нелинейное) через вектор:
Два преобразования выраженных через одну матрицу более высокой размерности:
