Почему множество Мандельброта устроено так, как оно устроено03.11.2020 10:02

Созерцание фракталов завораживает, особенно это относится к предмету данной статьи, который демонстрирует вдобавок ко всему еще и изрядное разнообразие. Впрочем, не менее интересно попытаться разобраться, откуда что берётся, как из одного, в сущности, (пусть и комплексного) числа рождается всё это великолепие.
Если любопытно, добро пожаловать под кат.

О чём вообще речь.

Множество Мандельбро́та — это «множество таких точек C на комплексной плоскости, для которых рекуррентное соотношение $Z_{n+1} = Z_n^2 + C$ при $Z_0=0$ задаёт ограниченную последовательность» (вики).

Иными словами, на каждом шаге число возводится в квадрат и к нему добавляется константа. Начальное значение всегда (0, 0i), варьируется именно константа. Если за определенное число шагов последовательность осталась в заданных пределах, то значение константы принадлежит множеству. Выглядит это так: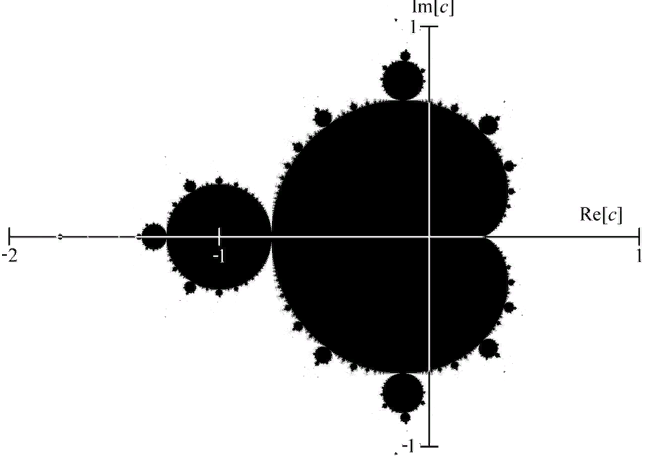

Фиг.1 Множество Мандельброта в координатах — реальная и мнимая части константы. Отсюда.

Чаще действуют по другому — фиксируют радиус и для каждого значения константы подсчитывают число итераций, за которое последовательность до него добралась. Это позволяет раскрасить пограничные области множества, не принадлежащие, впрочем, самому множеству.
Вот так, например:

Фиг.2 Типичная цветовая схема

И откуда же всё это берется?
Нельзя просто так вот взять и ответить на этот вопрос.
Начнём с малого, изучим простую казалось бы операцию — возведение в квадрат.

Основа,

Итак, что же это за возведение в квадрат комплексного числа, ведь именно оно лежит в основе наблюдаемой магии?

Комплексные числа будем рассматривать как двумерный вектор из реальной и мнимой части (что бы это ни означало) либо в полярных координатах как пару длина — угол.

Формула Муавра утверждает, что возведение комплексного числа в квадрат приводит к возведению длины в квадрат, угол при этом удваивается.

Фиг.3 Стартуем с угла 0.001 рад

Вот первые 12 итераций возведения в квадрат комплексного числа с длиной 1 и углом — 0.001 рад, где угол отсчитывается от действительной единицы против часовой стрелки. Когда угол превышает 2π, используется остаток от деления. Отрицательные углы тоже в деле.

Какие особенности есть у последовательности $Z→Z^2$ ?

Поскольку значение длины на каждой итерации возводится в квадрат, любое комплексное число с длиной меньше единицы стремится в центр координат.
Аналогично, любая последовательность со стартовой длиной больше единицы тут же стартует в бесконечность.
Интерес представляют лишь точки, расположенные на единичной окружности.
Точка (1, 0i) стационарная, угол равен 0 (или 2π), с неё последовательность не может уйти.
Точка (-1, 0i) соответствует углу в π, на следующей итерации превращается в 2π и становится стационарной.
Обобщим, точки с углом ± $\pi/2^n$ (n — целое неотрицательной число) также рано или поздно попадают в стационарную точку. Как и точки $\pi±\pi/2^n$ . Для отрицательных n — они уже там.
Точки с углом $±\pi/n$ (n — целое число, не являющееся степенью 2) образуют устойчивые циклы

Фиг.4 Последовательности для начальных углов в π/3, π/5, π/7, π/11
Забавно, циклы для π/n образуются по углам правильного n-угольника с одним из углов в стационарной точке (1,0i), но этот угол не посещается. Это проистекает из того, что, например, ( $2^n\mod{13}$ ) не может породить 0, а только лишь числа от 1 до 12.
Но это всё простые делители. Попробуем что-нибудь непростое и нечётное.

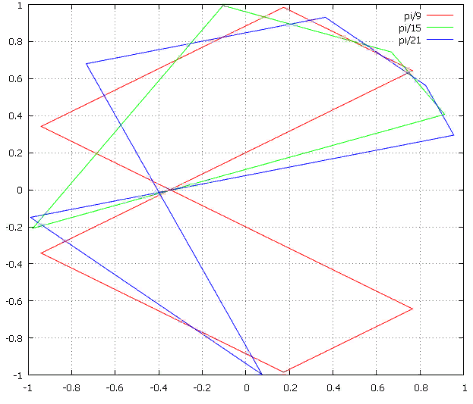
Фиг.5 Последовательности для начальных углов в π/9, π/15, π/21.
Похоже, все рациональные делители образуют устойчивые циклы.
Точки со стартовыми углами в ±π/x (x — иррациональное число) не образуют циклов и заметают всю окружность.

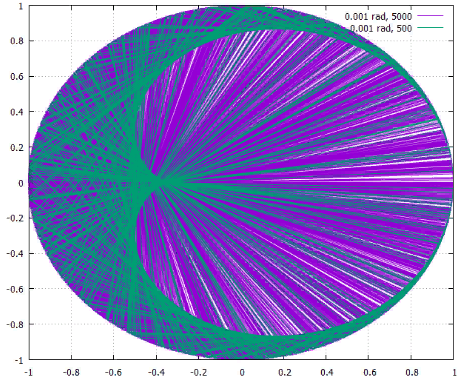
Фиг.6 Последовательность с началом в 0.001 рад
Здесь показаны первые 500 и 5000 точек из уже знакомой последовательности, начинающейся с угла 0.001 радиана.
Отлично видно проявившуюся кардиоидо-подобную структуру. Происхождение её очевидно, если поделить единичный круг на 8 секторов

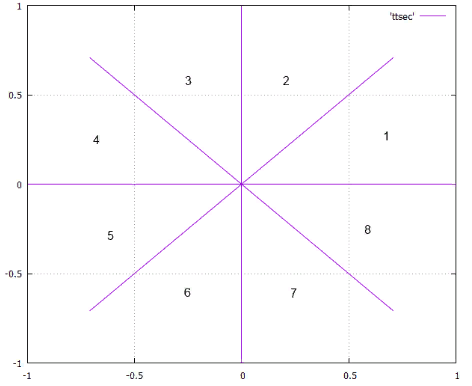
Фиг.7 Сектора
то в силу удвоения угла,
точки из сектора 1 могут попасть только в сектор 2 (или остаться в 1)
точки из сектора 2 могут попасть в сектора 3 и 4
точки из сектора 3 могут попасть в сектора 5 и 6
точки из сектора 4 могут попасть в сектора 7 и 8

К слову сказать, чтобы получить последовательность из 5000 адекватных значений, пришлось работать с точностью до 2000 значащих цифр. Фактически, каждая итерация последовательности приводит (грубо, за счет использования остатка от деления угла) к потере одного старшего разряда и подтягиванию одного разряда снизу, из «великого ничто». Понятно, в «великом ничто» точность неограниченна, нам же приходится работать с конечными объемами данных.

Малые возмущения

Сейчас немного отойдём от чистого $Z→Z^2$ в сторону исходной задачи. На каждой итерации станем подмешивать константу. Правда, стартовая точка будет не в начале координат, а на единичной окружности. В результате можно работать с очень маленькими константами, ведь в этом случае не требуется вытаскивать последовательность на окружность для демонстрации нетривиального поведения.

Константа — это просто вектор из начала координат. В зависимости от того, где находится текущая итерация последовательности на единичной окружности, константа действует по-разному. Иные точки она «задувает» внутрь «кратера», другие «сдувает» наружу. От баланса этих воздействий зависит, удержится ли последовательность в окрестностях единичной окружности или же безвозвратно уйдёт с дистанции.

Начнём со знакомой точки 0.001 радиана.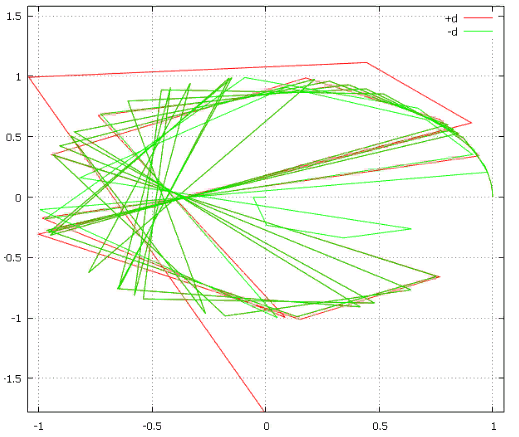

Фиг.8 Траектории при малых реальных отклонениях от 0.001 рад

Всего 58 итераций потребовалось, чтобы сойти с единичного круга и стремиться в бесконечность в случае константы (0, i*1e-15). При константе (0, i*-1e-15), последовательность ушла в 0 на 62 шагу.

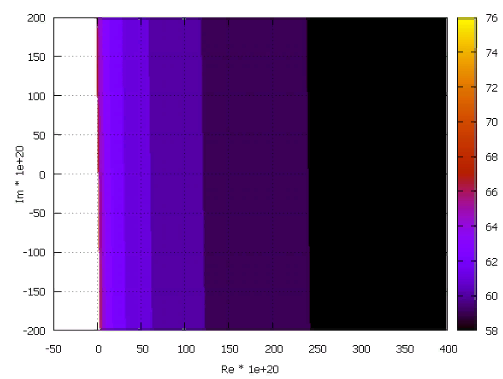
Фиг.9 Окрестность 0 константы для стартовой точки 0.001 рад

Здесь показано, на какой итерации последовательность пересекла круг с радиусом 2 в зависимости от величины комплексной константы. Шаг $10^{-20}$ . Отметим следующее:

Стартовая точка (длина 1, угол 0.001 рад) очень близка к горизонтальной оси. Соответственно, единичная окружность проходит через нее почти вертикально.
Первые несколько точек последовательности очень близки к стартовой, поэтому константа суммируется с ними одинаково.
Фактически, направление вектора константы однозначно определяет, в какую сторону соскользнёт последовательность.

Фиг.10 Окрестность 0 константы для стартовой точки 1⅓π рад

Здесь показан старт последовательности с точки с углом 1⅓π, это одна из точек цикла со стартом в π/3. Цикл состоит из двух точек — ⅔ и 1⅓π. Казалось бы, константа должна разнонаправленно действовать на эти точки, нивелируя саму себя. Но нет, никакой интриги и тут не видно. Куда направлен вектор константы по отношению к первой точке последовательности, туда и «сдувает» траекторию.

Пожалуй, на этом мы закончим с $Z→Z^2$ ,
в следующий раз займёмся центральной кардиоидой.
Сегодня мы уже встречались с кардиоидой, есть ли между ними связь или просто совпадение?
А может это сигнал «для тех кто понимает»?

PS: на заглавной иллюстрации оболочка Мандельброта — обобщение на трёхмерный случай.

PPS: для вычислений с произвольной точностью была использована библиотека MAPM.

PPPS: иллюстрации сделаны с помощью gnuplot.