Побитовые операции: для чего нужны основы информатики Solidity-разработчику22.04.2024 18:30

Перед тем как переходить к побитовым операциям необходимо понять (или вспомнить), а что такое вообще бит и байт.

Немного информатики

Бит — это наименьшая единица информации, символ или сигнал который может принимать только 2 значения: включено или выключено, да или нет, высокий или низкий, заряженный или незаряженный. Можно сказать что любая лампочка может стать битом — она либо включена, либо выключена. Соответственно в двоичной системе счисления бит это 0 или 1.

В общем если бит это кирпич, тогда стена из кирпичей — байт.

Байт — это уже совокупность битов, которые вычислительная машина может обрабатывать одновременно и так исторически сложилось что один байт в 99,9% случаев будет равняться 8 битам, потому что это оказалось удобно и эффективно. Крайний левый бит в байте является старшим (MSB — Most Significant Bit). Крайний правый — младшим (LSB — Least Significant Bit). Биты в байте нумеруются справа налево. Бит 0 является крайним правым и он наименьший. Бит 7 является крайним левым и он наибольший.

Важно!  Нумерация справа налево относится к прямому порядку битов, но существует и обратный порядок с нумерацией с лева направо, правда он встречается гораздо реже, поэтому все дальнейшие примеры будут в прямом порядке.

Есть отличная статья:  «Как два байта переслать», в которой показывается что будет на уровне байтов если отправить слово «Hello!» с одного компьютера на другой.

В бит мы можем положить только 0 или 1, знак минус туда не запишешь, а с отрицательными числами работать как-то нужно, поэтому на уровне битов существуют знаковые и беззнаковые числа. Дальше обо всем поподробнее.

Беззнаковые числа (положительные)

В одном байте (если мы говорим про беззнаковое число) содержатся значения от 0 до 255 или если в двоичном виде от 00000000 до 11111111.

Получается, что в байте — 8 бит. Каждый бит имеет свое порядковое место (позицию) в байте. В зависимости от той позиции где находится бит — меняется его вес. Вес — это число, которое получится если возвести 2 в степень той позиции на которой она стоит. Нулевая позиция — вес = 20 = 1, первая позиция — вес = 21 = 2, вторая позиция — вес = 22 = 4 и так далее.

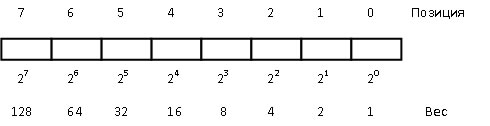
Чтобы запомнить можно потренироваться, например можно для начала взять только первые 4 позиции байта и перевести числа от 0 до 15 в двоичный код. Чтобы получить число 5 нам нужно сложить 22 + 20 потому что на второй позиции стоит число 4, а на нулевой число 1, получится 0101.

К примеру 10 в двоичной системе будет 1010, 13 = 1101, 14 = 1110 и т.д.

Таким образом имея 4 позиции мы можем оперировать числами от 0 до 15 потому что 23 + 22 + 21 + 20 = 15.

В этом видео буквально на пальцах объясняется почему так и как переводить числа из двоичной в десятичную.

А дальше можно попрактиковаться в переводе из двоичной в десятичную через онлайн-калькулятор, к примеру вот так будет выглядеть перевод числа 93 из двоичной системы в десятичную:

010111012 = 0 + 26 + 0 + 24 + 23 + 22 + 0 + 20 = 0 + 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310

Есть также видео по обратному переводу из десятичной в двоичную, а дальше снова можно попробовать сделать это на калькуляторе, к примеру вот так будет вычисляться двоичное число 35:

3510 = 1000112

Заметка: В стандартном приложении калькулятора некоторых операционных систем (win, macos) есть режим программирования, где можно производить все эти операции и не только.

Таким незамысловатым образом биты позволяют кодировать числа в двоичной системе счисления.

А вот так будет выглядеть 2 байта или 16 бит если их разложить на десятичные числа. 2 байта образуют машинное слово, но об этом в другой раз.

С этими знаниями уже можно двигаться дальше.

Знаковые числа (положительные и отрицательные)

Числа могут быть не только положительными, но и отрицательными. Это заставляет нас по-другому взглянуть на хранение чисел. Допустим, число 5 в двоичной форме выглядит как 00000101, но число -5 имеет точно такую же последовательность нулей и единиц, только с минусом. У нас нет специального обозначения, которое позволило бы хранить этот символ в памяти. Поэтому нужен специальный формат обозначения, по которому компьютер мог бы различать числа и понимать, какое число положительное, а какое отрицательное. Для этого существует прямой, обратный и дополнительный код. Это три разных представления как хранить отрицательные числа в двоичном коде.

Прямой код

Прямой код просто использует старший бит для обозначения знака числа. Однако это создает проблемы с обработкой отрицательного нуля и требует дополнительной обработки знакового бита.

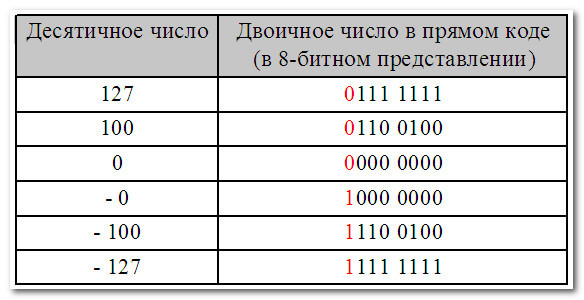
Обратный код

Обратный код решает некоторые из этих проблем, инвертируя все биты числа для создания его отрицательного эквивалента. Но он все еще сталкивается с проблемой отрицательного нуля.

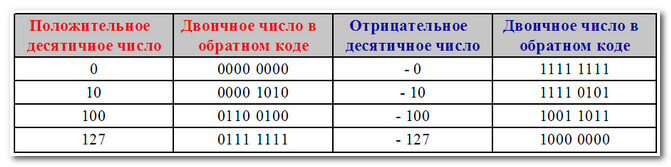
Дополнительный код

Дополнительный код, который используется в большинстве современных компьютеров, решает все эти проблемы, добавляя 1 к обратному коду числа. Это позволяет избавиться от отрицательного нуля, делает числа упорядоченными и расширяет диапазон чисел, которые можно представить.

Операция вычитания в дополнительном коде происходит путем добавления двух чисел, одно из которых представляет собой отрицательное число. Если результат сложения двух больших положительных чисел или двух больших отрицательных чисел не укладывается в диапазон чисел, которые можно представить, происходит переполнение. В этом случае результат будет на другой стороне диапазона чисел, на которую указывает количество шагов переполнения.

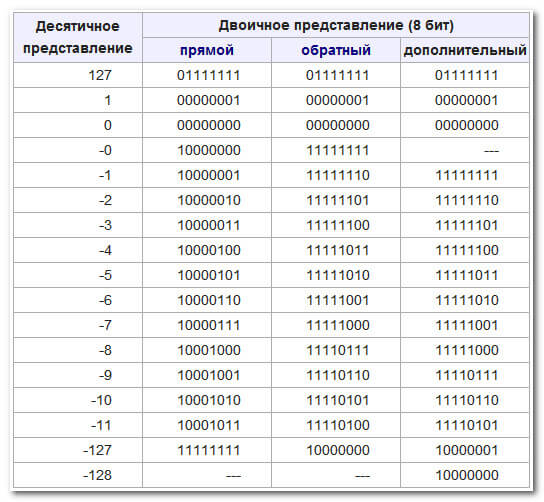
Форма записи чисел в дополнительном коде оказалась наиболее оптимальной как с точки зрения математики, так и с точки зрения упрощения архитектуры компьютера. Я очень рекомендую к просмотру это видео про отрицательные числа.

Вот теперь можно начать разбираться с битовыми операциями.

Битовые операции

Битовые операции — это особый тип операций в вычислениях, который позволяет манипулировать битами данных напрямую. Они работают на уровне отдельных битов в двоичном представлении чисел.

Во многих языках программирования очень часто приходится работать с такими логическими операциями как:

• && — Логическое И (AND)

• || — Логическое ИЛИ (OR)

• ! — Логическое НЕ (NOT)

• < > = — меньше, больше, равно и их комбинации

Вот к примеру таблицы истинности для операторов AND, OR и NOT:

AND

OR

NOT

Но эти операторы работают с числами или булевыми значениями (по факту с байтами) в то время как битовые операции работают на более низком уровне и к ним добавляется еще несколько операций, таким образом полный список битовых операций будет выглядеть так:

• &  — Побитовое И (AND)

• |  — Побитовое ИЛИ (OR)

• ^  — Исключающее ИЛИ (XOR)

• ~  — Побитовое отрицание (NOT)

• << — Побитовый сдвиг влево

• >> — Побитовый сдвиг вправо

Также добавляется еще одна таблица истинности для исключающего ИЛИ — XOR:

XOR

Таблицы для AND, OR, NOT работают также как и с логическими операциями, поэтому запомнить не сложно. Исключающее или дает 1 только когда операнды отличаются, а когда они одинаковые получаем 0.

Логические вентили

Фактически битовые операции в сочетании с запоминающими элементами это то, на чем строится вся вычислительная техника на самом низком уровне. Так как это базовые элементарные логические операции (их еще называют логические вентили) с которыми может работать непосредственно процессор используя напряжение и различные схемы. К примеру так будет выглядеть схема оператора отрицания NOT:

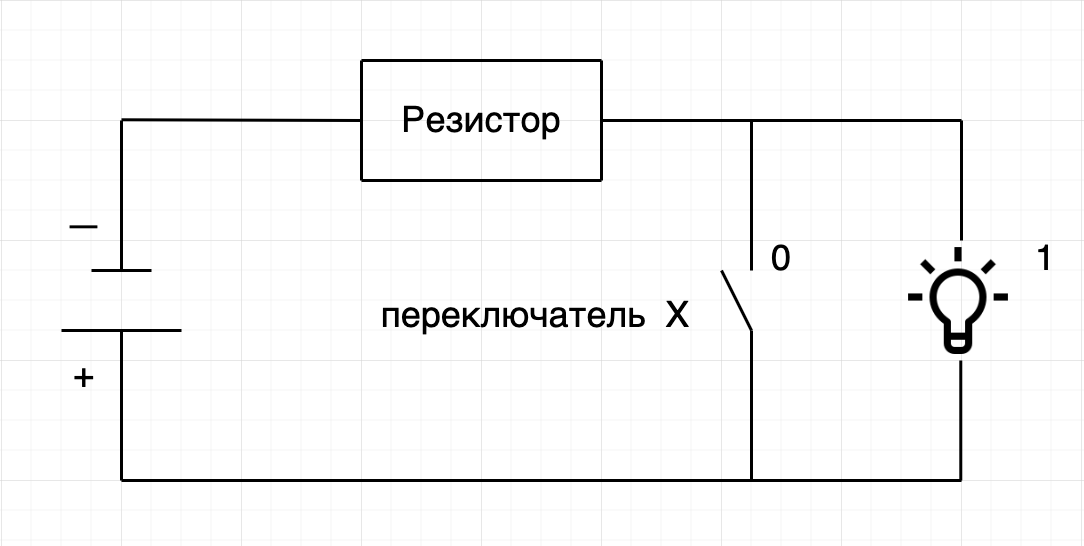
Схема элементарной логической операции NOT на уровне электроники

То есть если представить что лампочка это наличие напряжения или 1 на выходе, а Х это переключатель, то в случае когда переключатель замыкается ток на лампочку не идет и мы получаем 0, в противном случае будет 1.

А вот так будет выглядеть OR, то есть когда хотя бы один переключатель (x или y) замкнется на выходе мы получим напряжение:

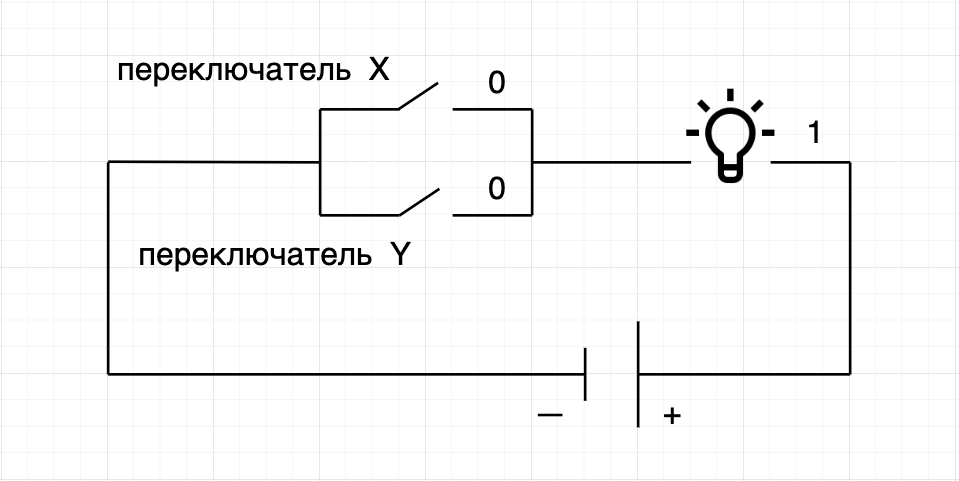
Схема элементарной логической операции OR на уровне электроники

В случае с AND нужно чтобы были замкнуты оба переключателя:

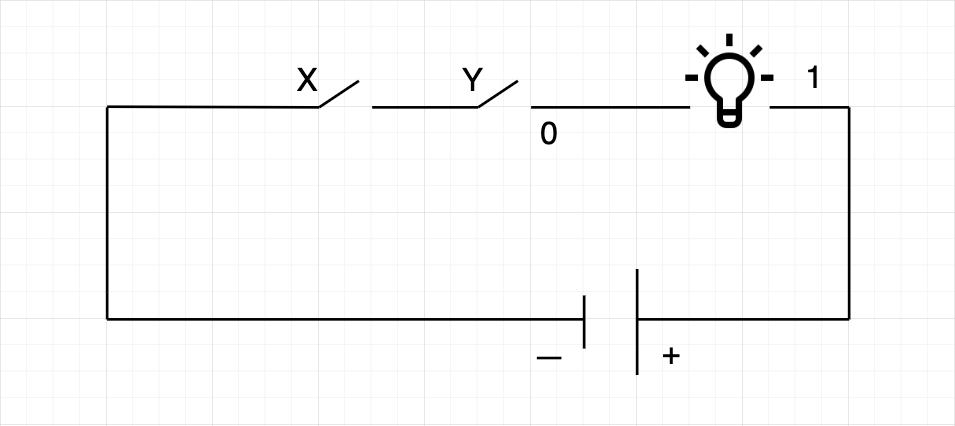
Схема элементарной логической операции AND на уровне электроники

Для XOR тоже есть электрическая схема, но в ней не обойтись без понятий из электрики вроде двухпозиционных переключателей, инверторов и т.д. Если интересно, можно почитать тут.

Простые действия с побитовыми операторами

Перед тем как изучать информацию ниже очень рекомендую это видео.

Итак, перейдем к примерам на уровне двоичного кода. Начнем с простого примера, если взять два числа 5 и 6 и применить к ним побитовый оператор & мы получим 4. Чтобы понять почему так произошло нужно перевести десятичные числа в двоичные и выполнить побитовое И (AND) с каждым отдельным битом применив таблицу истинности для AND:

    // x     = 101 = 4 + 0 + 1 = 5
    // y     = 110 = 4 + 2 + 0 = 6
    // x & y = 100 = 4 + 0 + 0 = 4
    function and(uint x, uint y) external pure returns (uint) {
        return x & y;
    }

Подобные примеры для остальных операторов можно посмотреть здесь, также можно посмотреть вот это видео. Это простой принцип, по которому будут работать все базовые побитовые операции. Единственный нюанс о котором стоит помнить, то что у нас может быть знаковое или беззнаковое двоичное число, к примеру если применить оператор ~ NOT к числу 8 (00001000) т.е. выполнить инверсию, в зависимости от того знаковый это тип или беззнаковый мы получим два разных числа.

    x  = 00001000 =   0 +  0 +  0 +  0 + 8 + 0 + 0 + 0 = 8
    ~x = 11110111 = 128 + 64 + 32 + 16 + 0 + 4 + 2 + 1 = 247 (unsigned)
    ~x = 11110111 =   0 +  0 +  0 +  0 + 8 + 0 + 0 + 0 + 1 = -9 (signed)

Помним что в дополнительном коде нам нужно прибавить единицу чтобы получить нужное отрицательное число.

Проверка бита

А теперь немного магии, которую можно творить использую битовые операции. Например мы храним три состояния в одном байте используя 3 последних бита. Нам нужно узнать что находится внутри отдельно взятого бита.

bytes1 state1 = 0x1; // 00000001
bytes1 state2 = 0x2; // 00000010
bytes1 state3 = 0x4; // 00000100

Чтобы это сделать нам нужно создать маску для нужного бита и применить оператор & AND, к примеру мы хотим получить значение второго бита:

    mask = 00000010

    00110010
  &
    00000010
    00000010 // result
    --------
    00110001
  &
    00000010
    00000000 // result

Таким образом если во втором бите что-то есть то мы получим 1, а если нет — там будет 0.

Изменение значения одного или нескольких битов с помощью OR и AND:

1. Установка бита в единицу

    00110000
  |
    00000010
    00110010

Тут мы поменяли второй бит на 1 применив побитовое ИЛИ | OR при этом оставив остальные биты такими же.

1. Установка бита в ноль (применим побитовое чтобы занулить второй бит)

    00110010
  &
    11111101
    00110000

А здесь занулили второй бит c использованием И & AND оставив другие биты нетронутыми.

Инвертирование отдельно взятых битов

Оператор ИСКЛЮЧАЮЩЕЕ ИЛИ ^ XOR позволяет инвертировать отдельно взятые биты. Чтобы это сделать возьмем как всегда второй бит и подставим туда 1. Если в втором бите был 0 то он превратится в единицу:

    00110000
  ^
    00000010
    00110010

И наоборот если там была 1 она станет 0:

   00110010
 ^
   00000010
   00110000

Здесь нет ничего сложного, но чтобы написать соответствующие функции для работы с отдельными битами нужно разобраться с еще одной темой — битовые сдвиги.

Битовые сдвиги

Вообще существует три вида побитовых сдвигов:

• Арифметический сдвиг << >>

• Логический <<< >>>

• Циклический <<<< >>>>

Тут все зависит от того, какой язык программирования используется. Сдвиги бывают в левую << и правую >> сторону.

Арифметический сдвиг

В случае арифметического сдвига вправо >> будет произведен сдвиг всех битов на n позиций вправо, а освободившийся старший бит будет заполнен битом знака: если число положительно — 0, если отрицательное — 1.

Арифметический сдвиг вправо

Запись сдвига числа 8 на одну позицию будет выглядеть так:  8 >> 1 (слева число, справа — на сколько бит нужно произвести сдвиг)

    00001000 >> 1 = 00000100 // 8 >> 1 = 4

В данном случае получаем 4.

При арифметическом сдвиге влево << будет произведен сдвиг всех битов на n позиций в лево, а младший бит будет заполнен 0.

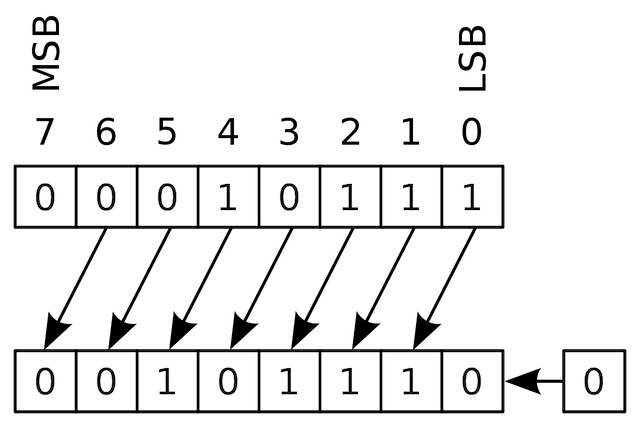
Арифметический сдвиг влево

Сдвинем 8 на одну позицию влево 8 << 1 и получим число 16.

    00001000 << 1 = 00010000 // 8 << 1 = 16

Таким образом мы получаем быстрый способ умножения или деления числа на 2n

    n << 1 == n * 2   |   n >> 1 == n / 2
    n << 2 == n * 4   |   n >> 2 == n / 4
    n << 3 == n * 8   |   n >> 1 == n / 8

Важно!  Деление происходит с округлением в меньшую сторону, например 9 >> 1 = 4.

Сдвиг вправо числа (-1) всегда будет давать (-1), выглядеть это будет так:

    11111111 >> 1 = 11111111 // -1 >> 1 = -1

Потому что как мы помним при сдвиге числа вправо старший бит заполняется битом знака, у отрицательно числа это 1.

Логический сдвиг

В случае с логическим сдвигом освободившийся бит всегда будет заполняться 0, как при сдвиге вправо >>> так и при сдвиге влево <<<. Такой сдвиг еще называют беззнаковым сдвигом.

    01000001 <<< 1 = 10000010 //  65 <<< 1 = 130
    10000001 >>> 1 = 01000000 // 129 >>> 1 = 64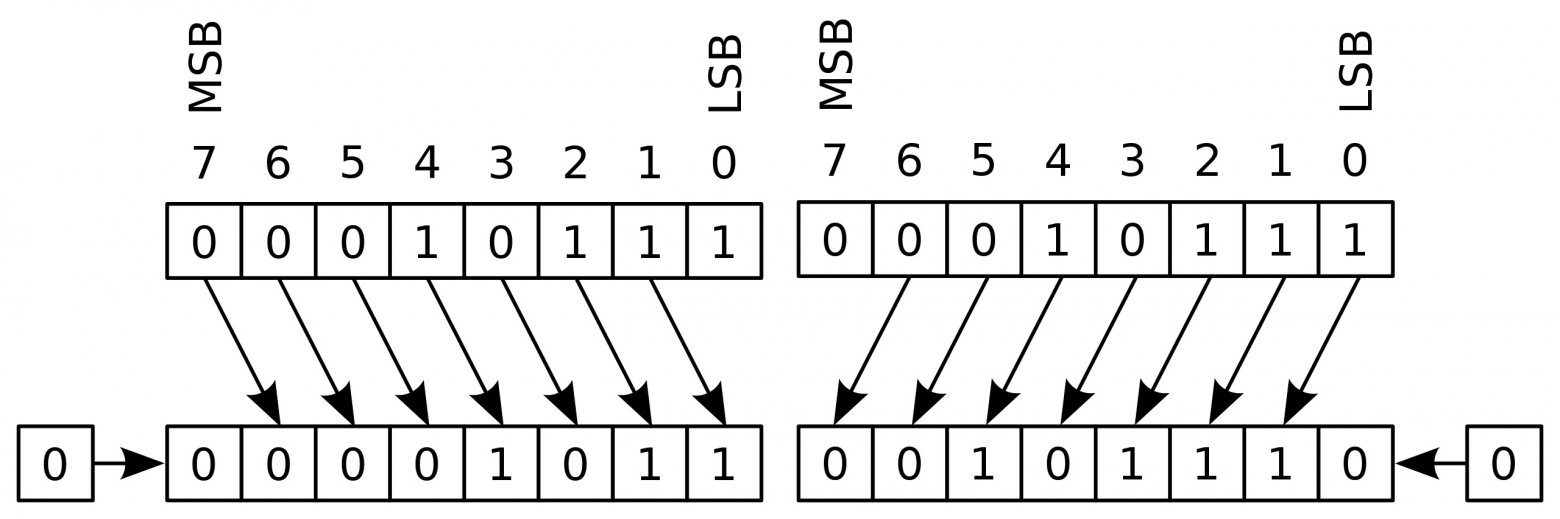

Логический сдвиг вправо и влево

Важно! Логический сдвиг применим только к беззнаковым числам.

Циклический сдвиг

Когда выполняется циклический сдвиг влево <<<< или вправо >>>> вышедший за пределы регистра старший или младший бит переходит на противоположную сторону:

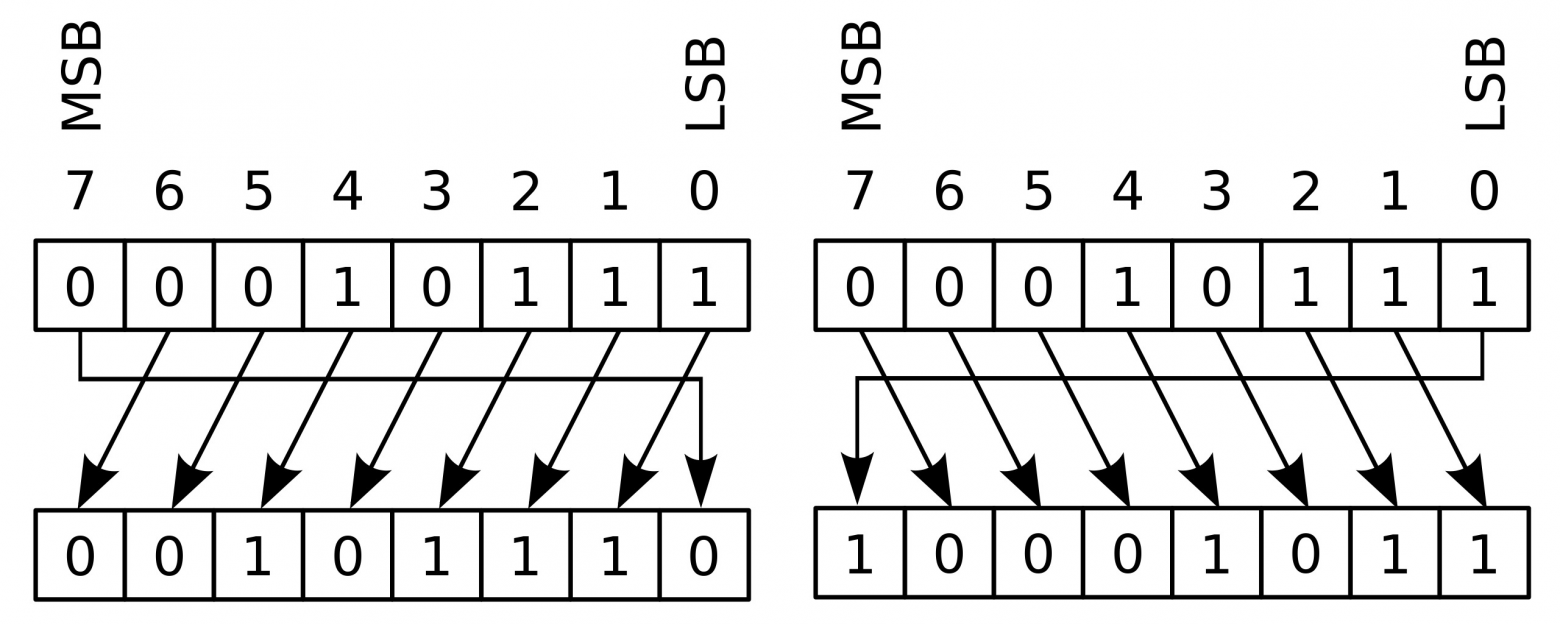
Важно! В Solidity используется только арифметический тип сдвига и только для беззнаковых чисел (uint).

Примеры кода на solidity

Теперь зная про сдвиги можно взять этот код и потыкать в Remix. Это 4 примера использования побитовых операций которые мы разбирали выше:

• Проверка отдельно взятого бита

• Установка отдельно взятого бита в 1

• Установка отдельно взятого бита в 0

• Инверсия отдельно взятого бита

Также теперь можно разобрать оставшиеся примеры со сдвигами тут. Более сложные операции и алгоритмы можно глянуть тут.

Варианты использования

1. Работа с флагами и масками.

Одним из главных применений битовых операций является работа с флагами и масками. В разделе с поиском бита мы уже использовали оба подхода. Флаги — это биты, которые используются для представления состояний или свойств объектов или систем. Битовые операции позволяют установить или сбросить определенные биты, что удобно для управления флагами. Также с помощью масок (последовательности битов) можно выбирать или скрывать определенные свойства объекта или данных.

Изящный пример работы с флагами в solidity можно увидеть в контракте Universal Router от Uniswap где они в один байт зашивают большое количество команд.

2. Компактное представление данных.

Битовые операции позволяют компактно хранить и передавать данные. Несколько булевых флагов мы можем объединить в одно число и использовать битовые операции для чтения или записи каждого флага отдельно. Это экономит память и упрощает работу с данными.

К примеру в solidity тип bool храниться в uint8, если взять uint8 и хранить каждый флаг в отдельном бите можно поместить в него 8 булевых значений.

3. Оптимизация производительности.

Операции над битами выполняются намного быстрее, чем стандартные арифметические операции или условные выражения. Использование битовых операций особенно полезно в смарт-контрактах на блокчейне, где за каждую операцию нужно платить газ и оптимизация кода является критически важной для снижения расходов на выполнение кода.

4. Шифрование и хеширование.

Битовые операции играют важную роль в шифровании данных и создании хешей. Многие алгоритмы шифрования и хеширования используют битовые операции для обработки данных на уровне битов. Это помогает обеспечить безопасность данных и уникальность хешей.

5. Работа с аппаратным обеспечением.

Битовые операции широко используются при программировании встроенных систем и работы с аппаратным обеспечением. Они позволяют управлять регистрами устройств, отправлять и принимать битовые данные, а также выполнять другие задачи, связанные с низкоуровневым программированием.

Заключение

Битовые операции являются мощным инструментом, который предоставляет разработчикам возможности для более эффективной работы с данными, оптимизации кода и обеспечения безопасности. Они имеют широкое применение в различных областях программирования, включая блокчейн. Понимание битовых операций поможет использовать их преимущества в своих проектах и создавать более эффективный и производительный код.

P.S. Спасибо, что дочитали статью до конца, надеюсь, она была полезной и интересной. В нашей Blockchain Wiki мы публикуем еще больше полезного контента для тех, кто интересуется миром web3 и языком Solidity.

Ссылки:

© Habrahabr.ru