Планковские единицы: существует ли фундаментальный предел пространства и времени?08.03.2022 12:46

По поводу планковского масштаба в научно-популярных материалах творится большая путаница. Здесь сказывается основная проблема поп-физики: гуляя от дилетанта к дилетанту, суть вопроса деградирует с каждой итерацией. Выглядит это примерно так:

Учёный в интервью оговаривается, что «длина Планка — это минимальное значимое расстояние», что является сильным упрощением.
Журналисты и популисты передают фразу дальше, пока она не деформируется в «длина Планка — это как размер пикселя для Вселенной», что неверно.
Учёные замечают ошибку и начинают поправлять, чтобы устранить недоразумение: «Планковская длина не похожа на размер пикселя для Вселенной. Это как раз тот масштаб, где квантовая гравитация становится актуальной». Что, безусловно, правильно, но…
Научпоп пережёвывает это, пока понятие не трансформируется в «планковская длина никогда не была минимальным расстоянием, это заблуждение. Это просто масштаб, на котором наши нынешние теории разрушаются, и ничто не указывает на то, что мы не можем достичь меньших масштабов». Это звучит разумно, но неверно.

Так что будет полезным разобраться, откуда все-таки следуют эти единицы и, собственно, для чего они задают предел.
За последние 400 лет наука раздвинула границы нашего познания — от мельчайших субатомных частиц до самых больших спиральных галактик. Мы рождаемся с органами чувств, которые позволяют нам исследовать окружающий мир, и хотя наша сенсорика освещает непосредственное окружение, она также накладывает фундаментальные ограничения на восприятие. Зрение предоставляет нам 90% информации, которая обусловлена поглощением и излучением квантов света электронами на внешних оболочках — жалкие полтора электронвольта! Но в мире существует ещё множество процессов, происходящих в разных масштабах энергий и длин.

Современная наука расширила диапазон наших чувств благодаря использованию технологий, позволяющих исследовать все более мелкие структуры, раскрывающие хитросплетения гобелена микрокосма. История показала, что чем глубже мы проникаем, тем больше мы обнаруживаем, но есть ли предел тому, как глубоко мы можем зайти? Существует ли фундаментальный нижний предел размера, который может иметь объект или область пространства? И если да, то можно ли его рассчитать?

▍ Самая слабая сила

Попытаемся ответить на кажущийся простым школьный вопрос: что произойдёт, если попытаться сжать два электрона, приближая их все ближе и ближе друг к другу? Как помнится, электроны — это отрицательно заряженные фундаментальные частицы, которые в привычном нам мире обитают в окрестности массивных ядер. Заряженные, значит между ними возникает электростатическая сила отталкивания (сила Кулона):

$F_E = \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2} = k\frac{e^2}{r^2}$

С другой стороны, электроны обладают массой, а следовательно, возникает гравитационная сила притяжения:

$F_G = G\frac{m_1m_2}{r^2} = G\frac{m_e^2}{r^2}$

Используемые величины

c = 299792458 # m/s     скорость света
ħ = 1.0546e-34 # J*s     постоянная Планка
е = 1.6022e-19 # Kl       элементарный заряд
mₑ = 9.1094e-31 # kg    масса электрона
ε₀ = 8.8542e-12 # F/m   электрическая постоянная
k = 1/(4π*ε₀) # 8.987552e9 # N*m^2/q^2
                                      
G = 6.6743e-11 # м³·кг⁻¹·с⁻²  гравитационная постоянная
L_Pl = 1.616e-35 # м              длина Планка
m_Pl = 2.176434e-8  # кг       ширина Планка

Теперь полезно разобраться, какая из этих двух сил больше. Для этого найдём их отношение:

$\frac{F_E}{F_G} = \frac{ke^2}{Gm_e^2} \approx 10^{42}$

Первое, что мы замечаем, это то, что величина r исчезает. То есть, независимо от расстояния между двумя электронами, отношение двух сил всегда должно быть одинаковым. Вполне ожидаемо, ведь они подчиняются закону обратных квадратов. Во-вторых, пугает разница в сорок два порядка — электростатическая сила больше гравитационной в тредециллион раз! Миллион миллиардов триллионов квадриллионов — кто круче назовет это число получит допуск к бонус-игре, где мы будем оценивать самую большую ошибку физики.

Простой расчёт говорит нам, что гравитационная сила невероятно мала, но ведь ей по силам собирать галактики и разрушать звёзды. Почему кажется, что она имеет бóльшую власть? Здесь следует вспомнить, что большинство атомов электрически нейтральны, то есть положительные заряды протонов компенсируются отрицательно заряженными электронами. Гравитация, насколько мы можем судить, отличается. Ее действие имеет некомпенсируемый аттрактивный характер, заставляющий стягиваться вещество с больших масштабов.

▍ Всё ближе

Наш анализ предполагает, что соотношение двух рассматриваемых сил не зависит от расстояния между электронами, но, как это часто бывает в фундаментальной физике, все не так просто, как кажется на первый взгляд. Например, принцип неопределённости Гейзенберга говорит, что по мере взаимного приближения рассматриваемых нами электронов, начинают действовать законы квантовой механики.

На некоммутирующие операторы накладывается ограничение:

$\Delta p \Delta x \geqslant\frac\hbar 2\\ \Delta p \gtrsim\frac{\hbar}{\Delta x}$

В конкретно этом случае имеется в виду, что нельзя с хорошей точностью одновременно определить импульс и положение частицы. Если вы представляли себе наши электроны как волновые пакеты или солитоны, то по мере приближения должна начать проявляться волновая природа: интерференция и вспучивание фронтов. Если же удобней оперировать точечными частицами, то при приближении электроны в вашем воображении претерпевают этакие дрожащие движения. Или же просто присмотримся к формуле выше и заметим, что по мере уменьшения расстояния увеличивается импульс системы. Сразу должны вспомниться закономерности для волн де Бройля.

Окей, у нас есть странное колебательное движение, а оно, в свою очередь, увеличивает энергию двух электронов, и как показал Эйнштейн, энергия может быть преобразована в массу и наоборот:

$\Delta E \sim mc^2$

Итак, в какой-то момент квантово-механическая энергия становится сравнимой с энергией массы, необходимой для создания нового электрона. Определим, на каком расстоянии это произойдёт. Для этого домножим соотношение неопределённости на скорость света:

$\begin{align} \Delta p & \gtrsim\frac{\hbar}{\Delta x = r}\\ \Delta E & \gtrsim\frac{\hbar c}{r}\\ m_ec^2 & \sim\frac{\hbar c}{r}\\ r & \sim\frac{\hbar}{m_ec}\approx 10^{-13}\,\mathrm m \end{align}$

Если подставить значения констант, то получим число порядка 10 в минус 13 метра, что меньше, чем типичный атом водорода (минус десятая степень), но больше типичного ядра (порядка 10 в минус 15 метров). Так что, преодолев предел в миллиардную долю миллиметра, мы достигаем масштаба, где энергия, порождаемая квантовомеханической неопределённостью, становится сопоставимой с энергией-массой целого электрона. При дальнейшем сближении электронов нужно учитывать увеличение массы системы, а значит, соотношение силы Кулона и гравитации будет меняться.

Гравитационная сила увеличивается и значит, в конце концов, она станет сопоставима с электростатической:

$\frac{F_E}{F_G}= \frac{ke^2}{Gm^2}\approx 1$

Теперь можно выразить массу, при которой это произойдёт и подставить в выражение для расстояния между электронами полученного из принципа неопределённости:

$\begin{align} m & \sim\sqrt\frac{ke^2}{G}\\ r & \leqslant\frac{\hbar}{mc}\approx 10^{-34}\,\mathrm m \end{align}$

На масштабах порядка одной десятидециллионной доли метра самая слабая сила сопоставима с электростатикой. В форме строгого равенства это выражение называется комптоновской длиной волны. Но мы ведь можем двигаться дальше? Попробуем, но придётся провести небольшой экскурс в физику массивных плотных объектов.

▍ Чёрные дыры

Рассмотрим небольшую массу, расположенную на поверхности массивного сферического тела. Очевидно, между этими двумя массами существует гравитационная сила притяжения, и поэтому, чтобы оторвать маленькую массу от поверхности, нужно будет совершить некоторую работу:

$\begin{align} F &= \frac{GMm}{r^2}\\ dW &= Fdr = \frac{GMm}{r^2}\mathrm dr \end{align}$

А теперь хотелось бы не просто приподнять этот шарик, а унести его в неведанные дали (туда, где гравитация не достанет):

$W = \int_r^\infty \frac{GMm}{r^2}\mathrm dr = \left. -GMm\frac 1r \right|_r^\infty = \frac{GMm}{r}$

Если мы подкинем с поверхности массивного тела некую малую массу, то ее кинетическая энергия уйдёт на борьбу с гравитационным потенциалом. Таким образом, мы можем определить минимальную скорость, необходимую телу для освобождения из гравитационного колодца:

$\begin{align} \frac{mv^2}{2} = \frac{GMm}{r} \\ v = \sqrt\frac{2GM}{r} \end{align}$

Это скорость убегания (или вторая космическая). Для Юпитера она равна примерно 60 км/с, для Луны — 2 км/с, а для Земли — поспрашивайте первых попавшихся на глаза школьников и оцените в целом заинтересованность молодёжи в вопросах космоса.

Из уравнения видно, что скорость убегания зависит от двух факторов: массы и радиуса покидаемого тела. Можно сделать вывод, что чем плотнее объект, тем большую скорость нужно достигнуть, чтоб его покинуть. Тут естественно спросить, что произойдёт, если объект будет настолько плотным, что скорость убегания с его поверхности достигнет скорости света? В таком случае даже свет не сможет покинуть это массивное тело, и поэтому оно будет казаться чёрным. Объект высокой плотности, из которого не может выйти даже свет, называется черной дырой.

$\begin{align} c = \sqrt\frac{2GM}{r} \\ r_s = \frac{2GM}{c^2} \end{align}$

Здесь получено выражение, оценивающее критический радиус (радиус Шварцшильда) для массивного тела, при котором оно становится чёрной дырой. Так какое отношение это имеет к сжатию двух электронов? Если вы помните, по мере того как мы сжимаем два электрона всё ближе и ближе друг к другу, масса нашей системы увеличивается из-за принципа неопределённости и специальной теории относительности, так что, понятно, к чему дело идет. Если мы будем продолжать сжимать электроны во всё меньший и меньший объём пространства и при этом увеличивать количество содержащейся массы, то мы непременно создадим там чёрную дыру.

▍ Собираем всё вместе

Осталось объединить все предыдущие результаты: комбинация квантовой механики со специальной теорией относительности позволяет оценить, сколько гравитационной массы содержится в электронной системе, а масса связана с радиусом Шварцшильда:

$\left.\begin{matrix} r\sim\frac{\hbar}{mc}\\ \\ r\sim\frac{Gm}{c^2} \end{matrix}\right\} r\sim\sqrt\frac{G\hbar}{c^3}\approx 10^{-35}\,\mathrm m$

Другими словами, если мы втиснем наши два электрона в объём пространства, примерно равный ста миллиардным иоктометра, то образуется чёрная дыра, так что мы оказываемся в ситуации, когда пытаемся выяснить, что происходит внутри этой области пространства при всё более высоких энергиях.

С иллюстрацией будет понятней:

Код

m = sqrt(k*е^2 / G) 
M = (8:0.01:16) * m
λ_c = ħ ./ (M*c)
R_s = G*M / c^2
plot( M/m_Pl, λ_c/L_Pl, lab = "λ_c", line = 4, yaxis = "r")
plot!(M/m_Pl, R_s/L_Pl, lab = "R_S", line = 4, xaxis = "m")

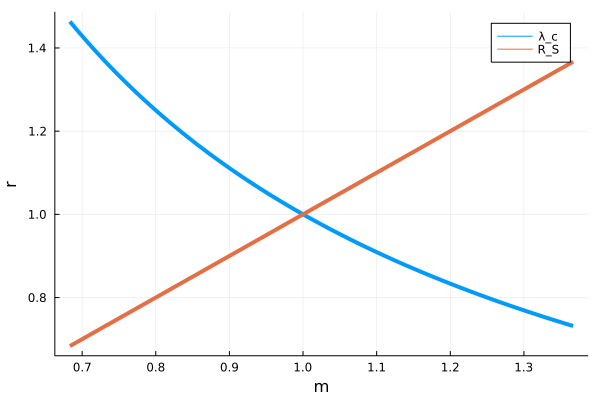
Встреча двух миров (оси в планковских единицах)

Мы стремимся ко всё меньшим масштабам длины, но попадаем в мир всё больших энергий — с уменьшением комптоновской длины волны, растёт масса системы (попытайтесь прикинуть, сколько электронов мы уже можем создать). Масса растёт, и с ней расширяется радиус Шварцшильда, пока чёрная дыра не поглотит всё то, что мы так старательно пытались рассмотреть.

Можно было бы и дальше пытаться добавлять в систему энергию, что только усугубит ситуацию: рост чёрной дыры ускорится. Значит не существует оперативного способа исследования природы на расстояниях меньше этой длины, которая известна как длина Планка и представляет собой фундаментальный нижний предел наших знаний о пространстве и масштабах расстояний, на которых мы можем осмысленно исследовать природу, и интересно отметить, что это ограничение в наших знаниях проявляется на масштабах длины, где квантовая механика, относительность и гравитация становятся одинаково важными. И пока мы ещё не устали, можно также рассчитать, сколько массы должно быть втиснуто в этот мизерный объём, чтобы образовалась чёрная дыра:

$m_p\sim\sqrt\frac{\hbar c}{G}\approx 22\,\mu\mathrm g$

Эта масса называется массой Планка и имеет значение примерно 22 микрограмма, что примерно равно массе блошиного яйца, так что довольно увлекательно размышлять о том, что фундаментальный предел самого пространства проявляется при сжатии блошиного яйца в пространство порядка 10 в минус 35 метров, что приводит к образованию чёрной дыры. Кто бы мог подумать!

сферы Блоха яйца блох

Обратите внимание, что если планковская длина кажется нижней границей всей физики, то планковская масса (или энергия) является границей между различными областями физики, а именно верхней границей массы фундаментальных частиц и нижней границей массы чёрной дыры. Поскольку чёрная дыра, должна испаряться до массы Планка из-за излучения Хокинга, можно ожидать, что она превратится в частицу (частицы), достигнув этого предела.

А как насчет планковского времени? Первое, что мы замечаем, когда подставляем числа, это то, что планковское время невероятно мало: 10 в минус 44 секунды. Так что же представляет собой это время? Ну, в самом простом смысле время Планка говорит нам, сколько времени потребуется свету, чтобы пройти путь, равный длине Планка. А ещё, в космологии Большого взрыва эпоха Планка это самый ранний этап истории Вселенной. В настоящее время не существует физической теории для описания таких коротких времен и не ясно, какой смысл имеет понятие времени для величин меньше времени Планка. Обычно предполагается, что квантовые эффекты гравитации доминируют над физическими взаимодействиями в этом масштабе времени. Люди часто спрашивают, что было до Большого взрыва, но правда в том, что мы сталкиваемся с проблемами даже не добравшись до него.

Еще примечательны планковская температура (15 дециллионов градусов Кельвина) и плотность (5 октовигинтиллионов (восемьдесят седьмая степень!) тонн на кубический сантиметр), но их оставим читателю на самостоятельное осмысление.

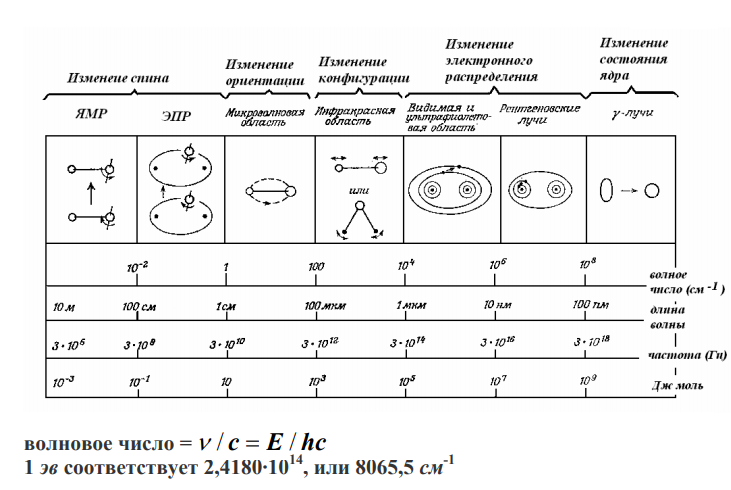
Постарайтесь насладиться концептом: с ростом прилагаемой энергии нам становятся доступны всё мельчайшие масштабы. Миллионы лет мы довольствовались информацией о метровых сгустках барионной материи, которые передавали нам сигналы благодаря процессам, умещающимся в нанометры. Затем мы лезем на внутренние оболочки атома, рассматриваем ядра и их составляющие. С ростом энергии мы видим всё больше сложновзаимодействующих компонент, пока не упираемся в непроходимую стену. Куда ни глянь, всюду чёрная дыра! Заполняет всё естество на самом фундаментальном уровне! Так что добавим себе в копилку досужих философствований Вселенную в чёрной дыре. Хотя это, разумеется, натягивание шварцшильдовской совы на однородный изотропный глобус Вселенной.

А теперь вернемся в реальный мир. Как и все оценки порядков величины, приведённая выше процедура не является строгой, поскольку она экстраполирует понятия чёрной дыры и комптоновской длины волны на масштаб, в котором оба явления, вероятно, потеряют свои общепринятые значения и, строго говоря, перестанут быть действительными. Однако именно таким образом мы приобретаем интуицию, двигаясь к неизведанной физике. Но любопытный читатель может найти более строгую теорию в ссылкографии.

▍ Послесловие

Конечно, все приведённые выше выкладки кажутся чрезмерно приблизительными. Но более классический путь базируется лишь на анализе размерностей, что выглядит куда умозрительнее. Зато мы добрались до рубежей современной физики, используя только школьные формулы, что не может не радовать. Хотя, на самом деле, теории, которые мы использовали, наверняка становятся недействительными, достигнув масштаба Планка.

Если мы используем релятивистскую квантовую механику и повышаем энергию до уровня, близкого к энергии Планка, то существует неограниченное количество гравитационных поправок, вступающих в дело по мере того, как сила гравитации становится всё больше и больше. Эти поправки являются «неконтролируемыми» и в какой-то момент делают теорию бесполезной (проблема ненормализуемости гравитации). И наоборот, если начать с общей теории относительности и уменьшать массу до значения, близкого к массе Планка, то появятся более высокие петлевые (квантовые) поправки, что приводит к той же проблеме. В принципе, и квантовая теория поля, и общая относительность должны быть заменены последовательной теорией квантовой гравитации, которая предстаёт во всей красе только при масштабе Планка, а на больших масштабах длины воспроизводит квантовую теорию поля и общую относительность.

В конце концов, можно принять одну из двух позиций: во-первых, что пространство и время реальны, что они действительно существуют, но мы просто не можем измерить их в этих экстремальных масштабах длины и времени. Другой вариант состоит в том, что пространство-время, как таковое, не существует в произвольно малых масштабах, и требуется кардинально иной подход. Можно предположить, что существуют атомы пространства-времени, и когда мы спускаемся до масштаба этих атомов, пространство-время перестает выглядеть как непрерывное многообразие точно так же, как деревянный стол перестает быть деревянным столом на квантовом уровне. Проблема с этой перспективой состоит в том, что на самом деле невероятно трудно придумать концепцию дискретности пространства-времени таким образом, чтобы она соответствовала законам специальной теории относительности.

Всё же, первая позиция привлекательней чем дискретная Вселенная. Довольно интересно думать о бурлящем и пузырящемся пространстве-времени, где на саму геометрию влияют квантовые неопределённости. Принцип неопределённости пространства и времени! И раз они подчиняются некоммутативной геометрии, то пространство можно было бы изучать и за планковскими границами за счет увеличения неопределённости времени. В любом случае, последнее слово за теорией квантовой гравитации.