Пишем XGBoost с нуля — часть 2: градиентый бустинг07.02.2019 13:04

Всем привет!

В прошлой статье мы разбирались, как устроены решающие деревья, и с нуля реализовали
алгоритм построения, попутно оптимизируя и улучшая его. В этой статье мы реализуем алгоритм градиентого бустинга и в конце создадим свой собственный XGBoost. Повествование будет идти по той же схеме: пишем алгоритм, описываем его, в заверешение подводим итоги, сравнивая результаты работы с аналогами из Sklearn’а.

В этой статье упор тоже будет сделан на реализацию в коде, поэтому всю теорию лучше почитать в другом вместе (например, в курсе ODS), и уже со знанием теории можно переходить к этой статье, так как тема достаточно сложная.

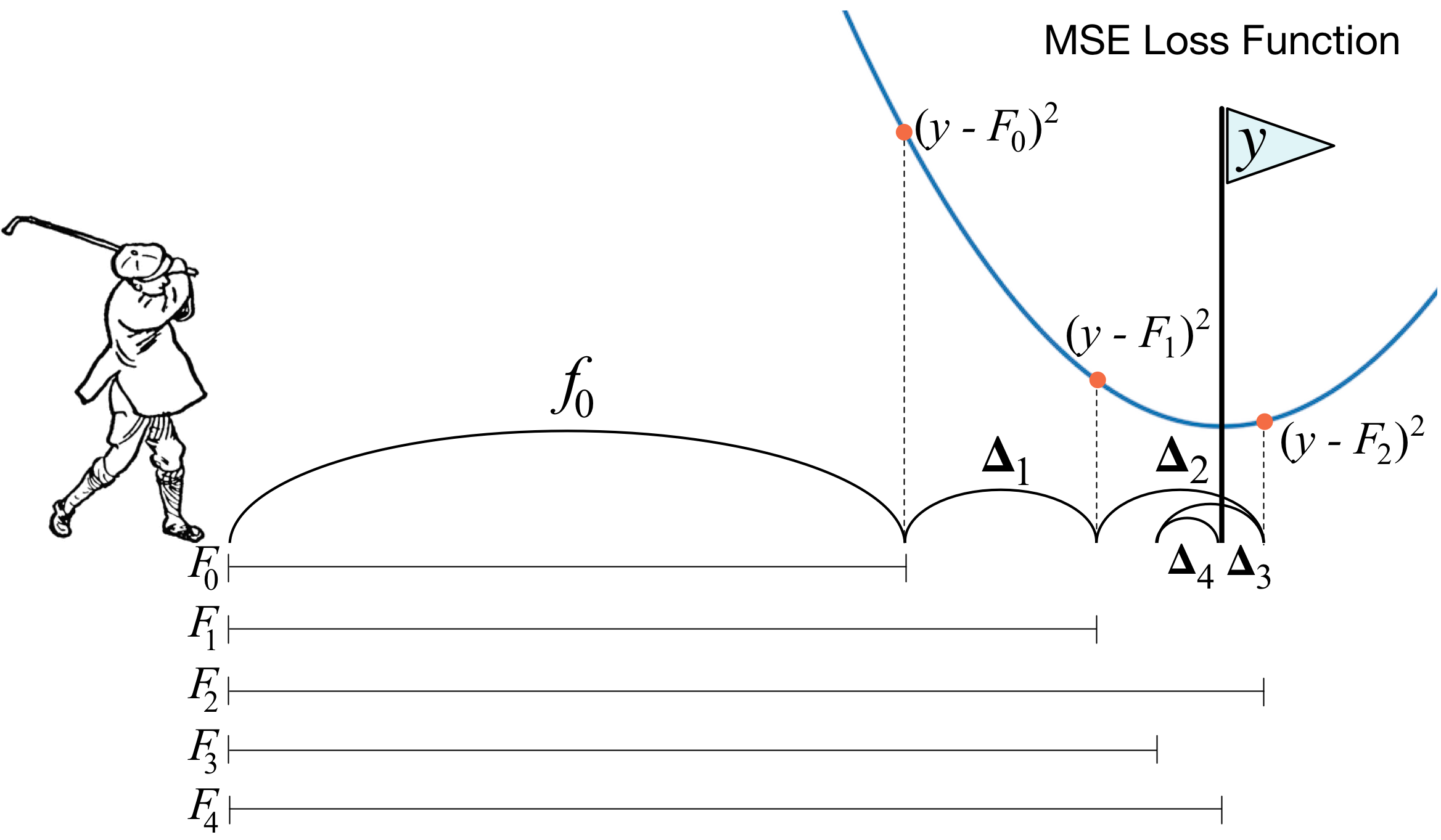
Что такое градиентный бустинг? Картинка с гольфистом как нельзя лучше описывает основную идею. Для того, что загнать мяч в лунку, гольфист делает каждый следующий удар с учётом опыта предыдущих ударов — для него это необходимое условие, чтобы загнать мяч в лунку. Еслиочень грубо (я не мастер игры в гольф :)), то при каждом новом ударе первое, на что смотрит гольфист, это на расстояние между мячом и лункой после предыдущего удара. И основная задача — следующим ударом уменьшить это расстояние.

Бустинг строится очень похожим способом. Во-первых, нам нужно ввести определение «лунки», то есть цели, к которой мы будем стремиться. Во-вторых, нам нужно научится понимать, в какую сторону нужно бить клюшкой, чтобы попасть ближе к цели. В-третьих, с учётом всех этих правил нужно придумать правильную последовательность ударов, чтобы каждый последующий сокращал расстояние между мячом и лункой.

Теперь дадим чуть более строгое определение. Введём модель взвешенного голосования:

$h(x) = \sum_{i=1}^nb_ia_i, x \in X, b_i \in R$

Здесь $X$ — это пространство, из которого берём объекты, $b_i, a_i$ — это коэффицент перед моделью и непосредственно сама модель, то есть дерево решений. Допустим, что уже на каком-то шаге с помощью описанных правил удалось добавить в композицию $T-1$ слабый алгоритм. Чтобы научиться понимать, какой-именно должен быть алгоритм на шаге $T$ , введем функцию ошибки:

$err(h) = \sum_{j=1}^N L(\sum_{i=1}^{T-1}a_ib_i(x_j) + b_Ta_T(x_j)) \rightarrow min_{a_T,b_T}$

Получается, что наилучшим алгоритмом будет тот, который сможет максимально уменьшать ошибку, полученную на предыдущих итерациях. И так как бустинг градиентный, то у этой функции ошибки обязательно должен существовать вектор антиградиента, вдоль которого можно двигаться в поисках минимума. Всё!

Непосредственно перед реализацией вставлю ещё пару слов о том, как именно у нас всё будет устроено. Как и в прошлой статье, в качестве лосса возьмем MSE. Посчитаем её градиент:

$mse(y,predict) = (y - predict)^2 \\ \nabla_{predict} mse(y,predict) = predict - y$

Таким образом, вектор антиградиента будет равен $y - predict$ . На шаге $i$ мы считаем ошибки алгоритма, полученного на прошлых итерациях. Далее обучаем наш новый алгоритм на этих ошибках, а затем со знаком минус и каким-то коэффициентом добавляем к нашему ансамблю.

Теперь приступим к реализации.

1. Реализация обычного класса градиентного бустинга

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm_notebook
from sklearn import datasets
from sklearn.metrics import mean_squared_error as mse
from sklearn.tree import DecisionTreeRegressor
import itertools
%matplotlib inline

%load_ext Cython

%%cython -a 

import itertools
import numpy as np
cimport numpy as np
from itertools import *

cdef class RegressionTreeFastMse:
    
    cdef public int max_depth
    cdef public int feature_idx
    cdef public int min_size
    cdef public int averages 
    
    cdef public np.float64_t feature_threshold
    cdef public np.float64_t value

    cpdef RegressionTreeFastMse left
    cpdef RegressionTreeFastMse right
    
    def __init__(self, max_depth=3, min_size=4, averages=1):
        
        self.max_depth = max_depth
        self.min_size = min_size
        self.value = 0
        self.feature_idx = -1
        self.feature_threshold = 0
        self.left = None
        self.right = None
    
    def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y):

        cpdef np.float64_t mean1 = 0.0
        cpdef np.float64_t mean2 = 0.0
        cpdef long N = X.shape[0]
        cpdef long N1 = X.shape[0]
        cpdef long N2 = 0
        cpdef np.float64_t delta1 = 0.0
        cpdef np.float64_t delta2 = 0.0
        cpdef np.float64_t sm1 = 0.0
        cpdef np.float64_t sm2 = 0.0
        cpdef list index_tuples
        cpdef list stuff
        cpdef long idx = 0
        
        cpdef np.float64_t prev_error1 = 0.0
        cpdef np.float64_t prev_error2 = 0.0
        cpdef long thres = 0
        cpdef np.float64_t error = 0.0
        
        cpdef np.ndarray[long, ndim=1] idxs
        
        cpdef np.float64_t x = 0.0
            
        # начальное значение - среднее значение y
        self.value = y.mean()
        # начальная ошибка - mse между значением в листе 
        base_error = ((y - self.value) ** 2).sum()
        error = base_error
        flag = 0
        
        # пришли на максимальную глубину
        if self.max_depth <= 1:
            return
    
        dim_shape = X.shape[1]
        
        left_value, right_value = 0, 0
        
        for feat in range(dim_shape):
            
            prev_error1, prev_error2 = base_error, 0 
            idxs = np.argsort(X[:, feat])
            
            # переменные для быстрого переброса суммы
            mean1, mean2 = y.mean(), 0
            sm1, sm2 = y.sum(), 0
            
            N = X.shape[0]
            N1, N2 = N, 0
            thres = 1
            
            while thres < N - 1:
                N1 -= 1
                N2 += 1

                idx = idxs[thres]
                x = X[idx, feat]
                
                # вычисляем дельты - по ним, в основном, будет делаться переброс
                delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1
                delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2

                # увеличиваем суммы
                sm1 -= y[idx]
                sm2 += y[idx]
                
                # пересчитываем ошибки за O(1)
                prev_error1 += (delta1**2) * N1 
                prev_error1 -= (y[idx] - mean1)**2 
                prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1)
                mean1 = sm1/N1
                
                prev_error2 += (delta2**2) * N2 
                prev_error2 += (y[idx] - mean2)**2 
                prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2)
                mean2 = sm2/N2
                
                # пропускаем близкие друг к другу значения
                if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5:
                    thres += 1
                    continue
                
                if (prev_error1 + prev_error2 < error):
                    if (min(N1,N2) > self.min_size):
                    
                        # переопределяем самый лучший признак и границу по нему
                        self.feature_idx, self.feature_threshold = feat, x
                        # переопределяем значения в листах
                        left_value, right_value = mean1, mean2

                        # флаг - значит сделали хороший сплит
                        flag = 1
                        error = prev_error1 + prev_error2
                                     
                thres += 1
        
        # ничего не разделили, выходим
        if self.feature_idx == -1:
            return
        
        # вызываем потомков дерева
        self.left = RegressionTreeFastMse(self.max_depth - 1)
        self.left.value = left_value
        self.right = RegressionTreeFastMse(self.max_depth - 1)
        self.right.value = right_value
        
        # новые индексы для обучения потомков
        idxs_l = (X[:, self.feature_idx] > self.feature_threshold)
        idxs_r = (X[:, self.feature_idx] <= self.feature_threshold)
        
        # обучение потомков
        self.left.fit(X[idxs_l, :], y[idxs_l])
        self.right.fit(X[idxs_r, :], y[idxs_r])
        
    def __predict(self, np.ndarray[np.float64_t, ndim=1] x):
        
        if self.feature_idx == -1:
            return self.value
        
        if x[self.feature_idx] > self.feature_threshold:
            return self.left.__predict(x)
        else:
            return self.right.__predict(x)
        
    def predict(self, np.ndarray[np.float64_t, ndim=2] X):
            
        y = np.zeros(X.shape[0])
        for i in range(X.shape[0]):
            y[i] = self.__predict(X[i])
            
        return y

class GradientBoosting():
    
    def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, 
                 random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'):
            
        self.n_estimators = n_estimators
        self.max_depth = max_depth
        self.learning_rate = learning_rate
        self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]])
        self.min_size = min_size
        self.loss_by_iter = []
        self.trees_ = []
        self.loss_by_iter_test = []
        self.n_samples = n_samples
        self.base_tree = base_tree

    
    def fit(self, X, y):
        self.X = X
        self.y = y
        b = self.initialization(y)
        
        prediction = b.copy()
        
        for t in tqdm_notebook(range(self.n_estimators)):               
            
            if t == 0:
                resid = y
            else:
                # сразу пишем антиградиент
                resid = (y - prediction)
            
            # выбираем базовый алгоритм
            if self.base_tree == 'Bagging':
                tree = Bagging(max_depth=self.max_depth,
                                       min_size = self.min_size)                
            if self.base_tree == 'Tree':
                tree = RegressionTreeFastMse(max_depth=self.max_depth,
                                          min_size = self.min_size)
                
            # обучаемся на векторе антиградиента
            tree.fit(X, resid)
            # делаем предикт и добавляем алгоритм к ансамблю
            b = tree.predict(X).reshape([X.shape[0]])
            self.trees_.append(tree)
            prediction += self.learning_rate * b
            # добавляем только если не первая итерация
            if t > 0:
                self.loss_by_iter.append(mse(y,prediction))
                   
        return self
    
    def predict(self, X):
        
        # сначала прогноз – это просто вектор из средних значений ответов на обучении
        pred = np.ones([X.shape[0]]) * np.mean(self.y)
        # добавляем прогнозы деревьев
        for t in range(self.n_estimators):
            pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]])
            
        return pred

Построим теперь кривую лосса на обучающей выборке, чтобы убедиться, что при каждой итерации у нас действительно происходит его уменьшение.

GDB = GradientBoosting(n_estimators=50)
GDB.fit(X,y)
x = GDB.predict(X)
plt.grid()
plt.title('Loss by iterations')
plt.plot(GDB.loss_by_iter)

2. Бэггинг над решающими деревьями

Отлично, перед тем как сравнивать результаты, давайте поговорим ещё и о процедуре бэггинга над деревьями.

Тут вс просто: мы хотим защититься от переобучения, и поэтому с помощью выборок с возращением будем усреднять наши предсказания, чтобы случайно не напороться на выбросы (почему это так работает — лучше почитайте по ссылке).

class Bagging():
    
    '''
    Класс Bagging - предназначен для генерирования бустрапированного
    выбора моделей.
    '''
    
    def __init__(self, max_depth = 3, min_size=10, n_samples = 10):
            
        #super(CART, self).__init__()
        self.max_depth = max_depth
        self.min_size = min_size
        self.n_samples = n_samples
        self.subsample_size = None
        self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, 
                                min_size=self.min_size) for _ in range(self.n_samples)]

    def get_bootstrap_samples(self, data_train, y_train):
        
        # генерируем индексы выборок с возращением
        indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size))
        samples_train = data_train[indices]
        samples_y = y_train[indices]
        return samples_train, samples_y
    
    def fit(self, data_train, y_train):
        
        # обучаем каждую модель 
        self.subsample_size = int(data_train.shape[0])
        samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train)
        for i in range(self.n_samples):
            self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1))
        return self
        
    def predict(self, test_data):
        
        # для каждого объекта берём его средний предикт
        num_samples = test_data.shape[0]
        pred = []
        for i in range(self.n_samples):
            pred.append(self.list_of_Carts[i].predict(test_data))
        pred = np.array(pred).T

        return np.array([np.mean(pred[i]) for i in range(num_samples)])

Отлично, теперь в качестве базового алгоритма можем использовать не одно дерево, а бэггинг из деревьев — так мы, опять же, защитимся от переобучения.

3. Результаты

Сравним результаты наших алгоритмов.

from sklearn.model_selection import KFold
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn
import copy

def get_metrics(X,y,n_folds=2, model=None):
    kf = KFold(n_splits=n_folds, shuffle=True)
    kf.get_n_splits(X)

    er_list = []
    for train_index, test_index in tqdm_notebook(kf.split(X)):
        X_train, X_test = X[train_index], X[test_index]
        y_train, y_test = y[train_index], y[test_index]
        model.fit(X_train,y_train)
        predict = model.predict(X_test)
        er_list.append(mse(y_test, predict))
    
    return er_list

data = datasets.fetch_california_housing()
X = np.array(data.data)
y = np.array(data.target)
er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' ))
er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' ))
er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1))

%matplotlib inline
data = [er_sklearn_boosting, er_boosting, er_boobagg]
fig7, ax7 = plt.subplots()
ax7.set_title('')
ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag'])
plt.grid()
plt.show()

Получили:

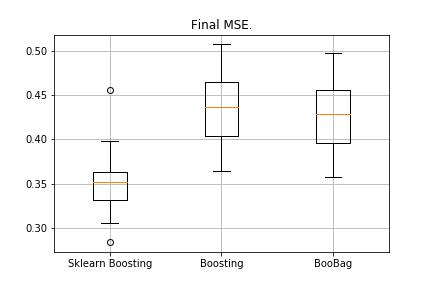
Мы пока не можем победить аналог из Sklearn, потому что опять не учитываем очень много параметров, которые используются в этом методе. Однако мы видим, что бэггинг чуть-чуть помогает.

Не будем отчаиваться, и перейдём к написанию XGBoost’а.

4. XGBoost

Прежде чем читать дальше, очень советую сначала ознакомиться со следующим видео, в нём очень хорошо объясняется теория.

Вспомним, какую ошибку мы минимизируем в обычном бустинге:

$err(h) = \sum_{j=1}^N L(\sum_{i=1}^{T-1}a_ib_i(x_j) + b_Ta_T(x_j))$

XGBoost явно добавляет регуляризацию в этот функционал ошибки:

$err(h) = \sum_{j=1}^N L(\sum_{i=1}^{T-1}a_ib_i(x_j) + b_Ta_T(x_j)) + \sum_{i=1}^T \omega(a_i)$

Как считать этот функционал? Сначала приближаем его с помощью ряда Тейлора второго порядка, где новый алгоритм рассматривается как приращение, вдоль которого мы будем двигаться, и дальше уже расписываем в зависимости от того, какой у нас лосс:

$f(x + \delta x) \thickapprox f(x) + f(x)' \delta x + 0.5* f(x)''(\delta x)^2$

Необходимо определить, какое дерево мы будем считать плохим, а какое хорошим.

Вспомним, на каком принципе построена с регрессия с $L_2$ -регуляризацией — чем больше по норме значения коэффициентов перед регрессией, тем хуже, поэтому нужно, чтобы они были как можно меньше.

В XGBoost идея очень похожа: дерево штрафуется, если сумма нормы значений в листьях в нём очень большая. Поэтому сложность дерева здесь вводится следующим образом:

$\omega(a) = \gamma Z + 0.5*\sum_{i=1}^{Z}w_i^2$

$w$ — значения в листьях, $Z$ — количество листьев.

В видео есть переходные формулы, мы их здесь выводить не будем. Всё сводится к тому, что новое разбиение мы будем выбирать, максимизируя gain:

$Gain = \frac{G_l^2}{S_l^2 + \lambda} + \frac{G_r^2}{S_r^2 + \lambda} - \frac{(G_l + G_r)^2}{S_l^2 + S_r^2 + \lambda} - \gamma$

Здесь $\gamma, \lambda$ — это числовые параметры регуляризации, а $G_i, S_i$ — соответствующие суммы из первых и вторых производных при данном разбиении.

Всё, теория очень кратко изложена, ссылки даны, теперь поговорим, какими будут производные, если мы работает с MSE. Всё просто:

$mse(y,predict) = (y - predict)^2 \\ \nabla_{predict} mse(y,predict) = predict - y \\ \nabla_{predict}^2 mse(y,predict) = 1$

Когда будем считать суммы $G_i, S_i$ , к первой просто прибавляем $predict - y$ , а ко второй — просто количество.

%%cython -a 

import numpy as np
cimport numpy as np

cdef class RegressionTreeGain:
    cdef public int max_depth
    cdef public np.float64_t gain
    cdef public np.float64_t lmd
    cdef public np.float64_t gmm
    
    cdef public int feature_idx
    cdef public int min_size

    cdef public np.float64_t feature_threshold
    cdef public np.float64_t value
    
    cpdef public RegressionTreeGain left
    cpdef public RegressionTreeGain right
    
    def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5):
        self.max_depth = max_depth
        self.gmm = gmm
        self.lmd = lmd
        self.left = None
        self.right = None
        self.feature_idx = -1
        self.feature_threshold = 0
        self.value = -1e9
        self.min_size = min_size
        
        return
    
    def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y):
        
        cpdef long N = X.shape[0]
        cpdef long N1 = X.shape[0]
        cpdef long N2 = 0
        cpdef long idx = 0
        cpdef long thres = 0
        cpdef np.float64_t gl, gr, gn
        cpdef np.ndarray[long, ndim=1] idxs
        cpdef np.float64_t x = 0.0
        cpdef np.float64_t best_gain = -self.gmm
        
        if self.value == -1e9:
            self.value = y.mean()
        
        base_error = ((y - self.value) ** 2).sum()
        error = base_error
        flag = 0
        
        if self.max_depth <= 1:
            return
        
        dim_shape = X.shape[1]
        
        left_value = 0
        right_value = 0
        
        # начинаем процесс обучения
        # чуть-чуть матана - у нас mse, L = (y - pred)**2
        # dL/dpred = pred - y, эту разницу мы в бустинге будем передавать со знаком -
        # dL^2/d^2pred = 1 - получается, это просто количество объектов в листе
        
        for feat in range(dim_shape):
            
            idxs = np.argsort(X[:, feat])
             
            gl,gr = y.sum(),0.0

            N1, N2, thres = N, 0, 0
            
            while thres < N - 1:
                N1 -= 1
                N2 += 1

                idx = idxs[thres]
                x = X[idx, feat]
                
                gl -= y[idx]
                gr += y[idx]
                
                # считаем гейн
                gn = (gl**2) / (N1 + self.lmd)  + (gr**2) / (N2 + self.lmd)
                gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm
                
                if thres < N - 1 and x == X[idxs[thres + 1], feat]:
                    thres += 1
                    continue
                
                # проверяем условия на гейн
                if (gn > best_gain) and (min(N1,N2) > self.min_size):
                    
                    flag = 1
                    best_gain = gn
                    left_value = -gl / (N1 + self.lmd)
                    right_value = -gr / (N2 + self.lmd)
                    
                    self.feature_idx = feat
                    self.feature_threshold = x

                thres += 1
        
        self.gain = best_gain
        if self.feature_idx == -1:
            return
                
        self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd)
        self.left.value = left_value
        self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd)
        self.right.value = right_value
        
        idxs_l = (X[:, self.feature_idx] > self.feature_threshold)
        idxs_r = (X[:, self.feature_idx] <= self.feature_threshold)
    
        self.left.fit(X[idxs_l, :], y[idxs_l])
        self.right.fit(X[idxs_r, :], y[idxs_r])
        
        # подрубаем отрицательный гейн
        if (self.left.left == None or self.right.left == None):
            if self.gain < 0.0:
                self.left = None
                self.right = None
                self.feature_idx = -1

    def __predict(self, np.ndarray[np.float64_t, ndim=1] x):
        if self.feature_idx == -1:
            return self.value
        
        if x[self.feature_idx] > self.feature_threshold:
             return self.left.__predict(x)
        else:
            return self.right.__predict(x)
        
    def predict(self, np.ndarray[np.float64_t, ndim=2] X):
        y = np.zeros(X.shape[0])
        
        for i in range(X.shape[0]):
            y[i] = self.__predict(X[i])
            
        return y

Небольшое уточнение: чтобы формулы в деревьях с gain’ом были красивее, в бустинге обучаем таргет со знаком минус.

Слегка модифицируем наш бустинг, сделаем некоторые параметры адаптивными. Например, если замечаем, что лосс начал выходить на плато, то уменьшаем learning rate и увеличиваем max_depth у следующих эстиматоров. Также добавим новый бэггинг — теперь сделаем бустинг над бэггингами из деревьев с gain’ом:

class Bagging():
    
    def __init__(self, max_depth = 3, min_size=5, n_samples = 10):
            
        self.max_depth = max_depth
        self.min_size = min_size
        self.n_samples = n_samples
        self.subsample_size = None
        self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, 
                                min_size=self.min_size) for _ in range(self.n_samples)]

    
    def get_bootstrap_samples(self, data_train, y_train):
        
        indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size))
        samples_train = data_train[indices]
        samples_y = y_train[indices]
        return samples_train, samples_y
    
    def fit(self, data_train, y_train):
        
        self.subsample_size = int(data_train.shape[0])
        samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train)
        for i in range(self.n_samples):
            self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1))
        return self
        
    def predict(self, test_data):
        
        num_samples = test_data.shape[0]
        pred = []
        for i in range(self.n_samples):
            pred.append(self.list_of_Carts[i].predict(test_data))
        pred = np.array(pred).T

        return np.array([np.mean(pred[i]) for i in range(num_samples)])

class GradientBoosting():
    

    def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, 
                 random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'):
            
        self.n_estimators = n_estimators
        self.max_depth = max_depth
        self.learning_rate = learning_rate
        self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]])
        self.min_size = min_size
        self.loss_by_iter = []
        self.trees_ = []
        self.loss_by_iter_test = []
        self.n_samples = n_samples
        self.base_tree = base_tree

        # хотим как-то регулировать работу алгоритма на поздних итерациях
        # если ошибка застряла, то уменьшаем lr и увеличиваем max_depth
        self.add_to_max_depth = 1
        self.init_mse_board = 1.5
    
    def fit(self, X, y):
        print (self.base_tree)
        self.X = X
        self.y = y
        b = self.initialization(y)
        
        prediction = b.copy()
        
        for t in tqdm_notebook(range(self.n_estimators)):
                        
            if t == 0:
                resid = y
            else:
                resid = (y - prediction)
                if (mse(temp_resid,resid) < self.init_mse_board):
                    self.init_mse_board /= 1.5
                    self.add_to_max_depth += 1
                    self.learning_rate /= 1.1
                    # print ('Alert!', t, self.add_to_max_depth)
            
            if self.base_tree == 'Bagging':
                tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth,
                                         min_size = self.min_size)
                resid = -resid
                
            if self.base_tree == 'Tree':
                tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size)
                
            if self.base_tree == 'XGBoost':
                tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size)
                resid = -resid
                
            tree.fit(X, resid)
            b = tree.predict(X).reshape([X.shape[0]])
            # print (b.shape)
            self.trees_.append(tree)
            prediction += self.learning_rate * b
            temp_resid = resid

        return self
    
    def predict(self, X):
        
        # сначала прогноз – это просто вектор из средних значений ответов на обучении
        pred = np.ones([X.shape[0]]) * np.mean(self.y)
        # добавляем прогнозы деревьев
        for t in range(self.n_estimators):
            pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]])
            
        return pred

5. Результаты

По традиции, сравним результаты:

data = datasets.fetch_california_housing()
X = np.array(data.data)
y = np.array(data.target)

import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn

er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging'))
er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost'))
er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2))

%matplotlib inline
data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging]
fig7, ax7 = plt.subplots()
ax7.set_title('')
ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost',  'XGBooBag'])
plt.grid()
plt.show()

Картинка будет следующая:

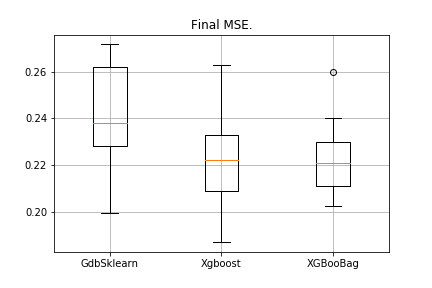
Самая низкая ошибка у XGBoost, но у XGBooBag ошибка более скученная, что определённо лучше: алгоритм более устойчив.

На этом всё. Очень надеюсь, что материал, изложенный в двух статьях, был полезен, и вы смогли узнать для себя что-то новое. Особую благодарность выражаю Дмитрию за всестороннюю обратную связь и исходники, Антону — за советы, Владимиру — за сложные задания по учебе.

Всем успехов!