Пересмотр системы единиц СИ: новые определения ампера, килограмма, кельвина и моля

Сфера из кремния-28 с чистотой 99,9998% может быть принята как эталон единицы измерения количества вещества, известной как моль (через число Авогадро). Фото: Национальная физическая лаборатория Великобритании
Международное бюро мер и весов планирует провести самую значительную реформу в международной системе единиц (СИ) со времени последней большой ревизии этого стандарта в 1960 году, пишет Nature. Придётся принимать новые ГОСТы, а также внести исправления в учебники физики в школе и вузах.
В настоящее время СИ (современный вариант метрической системы) принята в качестве основной системы единиц большинством стран мира и почти везде используется в области техники. Полное определение всех единиц СИ приведено в официальной брошюре (8-е издание) и дополнении к ней от 2014 года. Нынешний стандарт утверждён в СССР 1 января 1963 года ГОСТом 9867–61 «Международная система единиц».
Руководство международной организации проголосует за предложенные изменения на Генеральной конференции по мерам и весам в 2018 году, а в случае положительного решения изменения вступят в силу с мая 2019 года. Новые определения для единиц измерения и эталонов никак не отразится на жизни обывателей: один килограмм картофеля в магазине останется тем же килограммом картофеля. Весы будут измерять овощи и мясо с той же точностью, что и раньше. Но эти определения важны для учёных, потому что в научных исследованиях должна соблюдаться идеальная точность формулировок и измерений. Международное бюро мер и весов считает, что новые эталоны позволят «обеспечить высочайший уровень точности в различных способах измерений в любом месте и времени и в любом масштабе, без потери точности».
Итак, какие же изменения нас ждут?
Сейчас Международное бюро мер и весов намерено пересмотреть определения и эталоны следующих единиц измерения:
- ампер
- килограмм
- кельвин
- моль
Следует оговориться, что далее по тексту новые определения приводятся в сокращённом виде и не соответствует в точности тексту, который записан в официальном документе. Сам документ и окончательные значения констант опубликуют в ближайшее время.
Современное определение принято III Генеральной конференцией по мерам и весам (ГКМВ) в 1901 году и формулируется так: «Килограмм есть единица массы, равная массе международного прототипа килограмма». При этом Международный прототип (эталон) килограмма хранится в Международном бюро мер и весов (расположено в городе Севр неподалёку от Парижа) и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90% платины, 10% иридия). Размер прототипа примерно соответствует размеру мяча для гольфа.

Компьютерное изображение международного прототипа килограмма
Проблема с эталоном килограмма состоит в том, что любые материалы могут терять атомы или, наоборот, пополняться атомами из окружающего пространства. В частности, различные официальные копии эталонного килограмма, который хранится в Севре, отличаются по весу от официального эталона. Разница достигает 60 микрограмм. Такие изменения произошли за более чем 100 лет с момента создания копий.
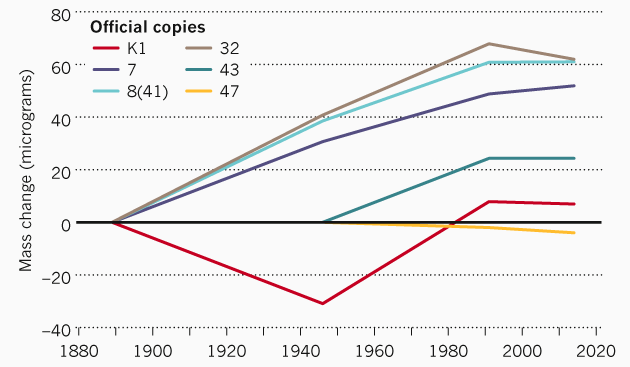
Ещё одна проблема с единицами измерения фиксированного масштаба — то, что элемент неопределённости (погрешность) увеличивается по мере удаления от этой фиксированной точки (эталона). Например, сейчас при измерении миллиграмма элемент неопределённости в 2500 раз больше, чем при измерении килограмма.
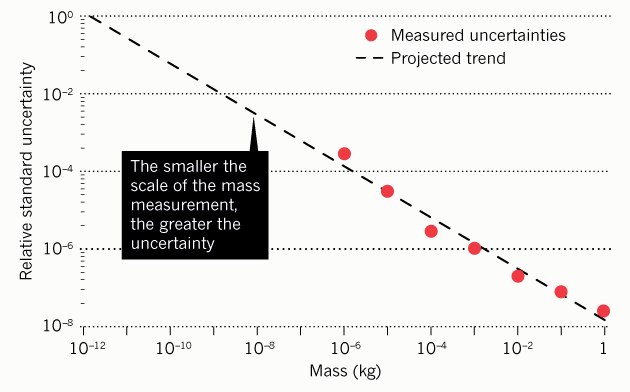
Эта проблема решается, если определить единицу измерения через другую физическую постоянную. Собственно, в новом определении килограмма так и сделано: здесь используется постоянная Планка.
Новое определение: 1 килограмм равен постоянной Планка, поделенной на 6,626070040 × 10−34 м−25. Для выражения единицы требуется постоянная Планка.
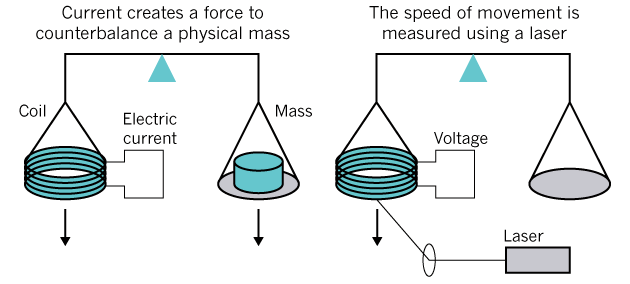
Измерение массы на практике возможно с помощью ваттовых весов: через два отдельных эксперимента со сравнением механической и электромагнитной силы, а затем путём перемещения катушки через магнитное поле для создания разности потенциалов (на иллюстрации внизу). Грубо говоря, масса вычисляется через электроэнергию, которая необходима, чтобы поднять предмет, лежащий на другой чаше весов.
Современное определение: как записано в ГОСТе, 1 кельвин равен 1/273,16 части термодинамической температуры тройной точки воды. Начало шкалы (0 К) совпадает с абсолютным нулём. В обязательном Техническом приложении к тексту Международной температурной шкалы МТШ‑90 Консультативный комитет по термометрии установил требования к изотопному составу воды при реализации температуры тройной точки воды.
Тройная точка воды — строго определённые значения температуры и давления, при которых вода может одновременно и равновесно существовать в виде трёх фаз — в твердом, жидком и газообразном состояниях.
Международный комитет мер и весов подтвердил, что определение кельвина относится к воде, чей изотопный состав определён следующими соотношениями:
0,00015576 моля 2H на один моль 1Н
0,0003799 моля 17О на один моль 16О
0,0020052 моля 18О на один моль 16О.
Проблемы современного определения очевидны. При практической реализации величиа кельвина зависит от изотопоного состава воды, а на практике практически невозможно добиться молекулярного состава воды, который соответствует Техническому приложению к тексту Международной температурной шкалы МТШ‑90.
Ещё в 2011 году на заседании Генеральной конференции по мерам и весам было предложено в будущей редакции Международной системы единиц переопределить кельвин, связав его со значением постоянной Больцмана. Таким образом, значение кельвина впервые будет точно зафиксировано.
Новое определение: 1 кельвин соответствует изменению тепловой энергии на 1,38064852 × 10−23 джоулей. Для выражения единицы требуется постоянная Больцмана.
Измерять точную температуру можно с помощью измерения скорости звука в сфере, заполненной газом. Скорость звука пропорциональна скорости перемещения атомов.
Современное определение: моль есть количество вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг. При применении моля структурные элементы должны быть специфицированы и могут быть атомами, молекулами, ионами, электронами и другими частицами или специфицированными группами частиц.
Новое определение: количество вещества системы, которая содержит 6,022140857 × 1023 специфицированных структурных единиц. Для выражения единицы требуется постоянная Авогадро (число Авогадро).
Для эталона числа Авогадро —, а через него и моля — учёные предлагают создать идеальную сферу из чистого кремния-28. У этого вещества идеально точная кристаллическая решётка, так что количество атомов в сфере можно определить, если точно измерить диаметр сферы (с помощью лазерной системы). В отличие от существующего куска платиново-иридевого сплава, скорость потери атомов кремния-28 точно предсказуема, что позволяет вносить коррективы в эталон.
Первые опыты по созданию такого эталона предприняли в 2007 году. Исследователи из берлинского Института выращивания кристаллов под руководством Хелге Риманна (Helge Riemann) приобрели в России обогащённый кремний-28 и сумели получить образец изотопа 28 с чистотой 99,994%. После этого исследователи ещё несколько лет анализировали состав 0,006% «лишних» атомов, определяли точный объём сферы и проводили рентгеноструктурный анализ. Изначально предполагалось, что «идеальные» сферы из кремния-28 могут быть утверждены в качестве нового стандарта для килограмма. Но сейчас более вероятно то, что их используют как эталон числа Авогадро и моля. Тем более что за время, прошедшее с 2007 года, физики научились производить гораздо более чистый кремний-28.

Сфера из кремния-28 с чистотой 99,9998. Фото: CSIRO Presicion Optics
В 2014 году американские физики сумели обогатить кремний-28 до беспрецедентного качества в 99,9998% в рамках международного проекта по расчёту числа Авогадро.
Современное определение предложено Международным комитетом мер и весов в 1946 году и принято IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году: «Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7 ньютона».
В современном определении ампер определяется через некий мысленный эксперимент, который предусматривает возникновение силы в двух проводах бесконечной длины. Очевидно, что на практике мы не может измерить такую силу, потому что по определению не может существовать двух проводников бесконечной длины.
Изменить определение ампера предложили на том же заседании Генеральной конференции по мерам и весам в октябре 2011 года, что и определение кельвина. Идея заключалась в том, что новое определение должно быть основано не на созданный человеком артефактах через мысленный эксперимент, а на фундаментальных физических постоянных или свойствах атомов. Итак, новое определение выражается только через одну постоянную — заряд электрона.
Новое определение: электрический ток, соответствующий потоку 1/1,6021766208 × 10−19 элементарных электрических зарядов в секунду. Для выражения единицы требуется заряд электрона.
На практике для определения ампера понадобится только один инструмент — одноэлектронный насос. Такие инструменты создали несколько лет назад. Они позволяют перемещать определённое количество электронов в течение каждого насосного цикла, что является крайне ценным качеством для фундаментальной науки и метрологии.
Определения секунды, метра и канделы, судя по всему, остаются неизменными, как показано на иллюстрации.
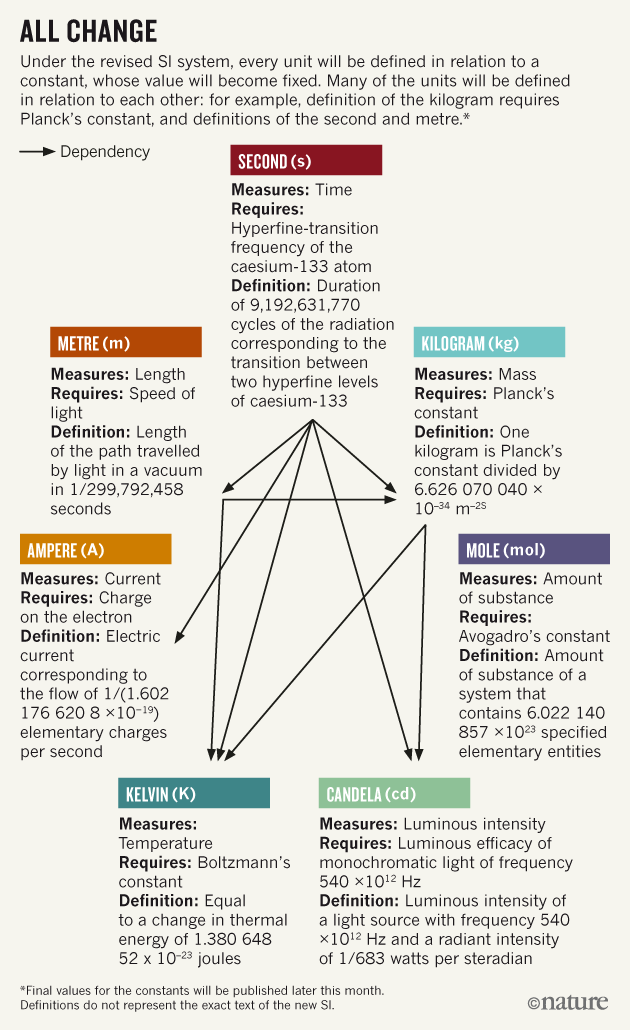
В новой системе СИ определение всех единиц выражается через константу с фиксированным значением. Многие единицы определяются во взаимосвязи с другими единицами. Например, определение килограмма определяется через постоянную Планка, а также через определения секунды и метра.
Считается, что такая система гораздо более устойчива и самодостаточна.
