Парсим строки с SMT-решателем22.08.2022 12:01

Этот пост о том, как можно разобрать строку по контектстно-свободной грамматике с помощью SMT-решателя. Здесь будет введение, описание принципа работы и ссылка на github с работающей программой.

План поста:

• Что такое SMT-решатель

• Формальные грамматики

  • Пример: лямбда-исчисление

  • Правила-суммы

  • Правила-произведения

• Переводим задачу парсинга на язык SMT-решателя

  • Константы

    • Символы грамматики

    • Группы ячеек

    • Подгруппа ячеек

    • Тип продукции

    • Номер ячейки в группе

  • Формулы

• Итоги

Что такое SMT-решатель

Попробую описать возможности этого инструмента в том объеме, который используется при разборе грамматики, не прибегая к строгим математическим определениям.

Константы

Представьте, что константа это такой ящик, в котором должно быть значение. На ящике написано имя константы. По имени мы можем отличить одну константу от другой. Формула это тоже как бы ящик, в котором обязательно лежат другие ящики: константы или формулы. Если в формулах есть 2 разных вхождения символа, обозначающего константу А, то эти вхождения символов обозначают одну и ту же константу. В каком-то смысле это закон нашей маленькой вселенной: если мы откроем ящики, на которых одинаковые имена, то мы увидим, что в них будут одинаковые значения.

Отношения

Значения констант могут состоять в отношениях. Если в отношении состоит пара значений, то такое отношение называется бинарным.

Так пара натуральных чисел (3, 4) состоит в бинарном отношении «меньше», а число 2 состоит в унарном отношении «быть положительным числом». Подумайте на досуге, что может быть нульарным отношением.

Логические связки

Формулы можно связать с помощью логических связок, например так: a < b & b < c. Здесь мы взяли 2 формулы и связали их логической связкой "И”. Получили формулу, которая истинна только когда оба её компонента истинны. Кстати, эту формулу в префиксном виде можно записать вот так: <(a, b) & <(b, c). 

Все логические связки: &, |, =>, ⇔. ~. Вы их хорошо знаете, не буду здесь их расписывать.

Что делает SMT решатель

Этот инструмент пытается найти такие значения констант, при которых все заданные формулы истинны. Если решение есть, то такой набор формул называется выполнимым (satisfiable). В противном случае — невыполнимым (unsatisfiable).

На вход решателя мы подаем набор констант и набор формул. На выходе получаем ответ SAT, если есть модель: значения констант, при которых формулы истинны, или ответ UNSAT, если для заданного набора формул (теории) не существует модели. Если модель нашлась, то можно попросить SMT решатель её вывести в терминал.

Моделью называется такой набор значений констант, при котором заданные формулы становятся истинны. Набор формул называется теорией.

Аббревиатура SMT означает «satisfiability modulo theories», на русский язык это можно перевести как «выполнимость формул в теориях».

Простые примеры

Здесь мы будем использовать SMT-решатель z3 и язык SMT-LIB 2. Это лиспо-подобный язык, в котором используется префиксная форма записи формул.

Есть сайт, на котором можно поиграться с формулами, не устанавливая z3: https://compsys-tools.ens-lyon.fr/z3/index.php. Update: подсказали песочницу от microsoft: https://microsoft.github.io/z3guide/playground/Freeform Editing

Выполнимая задача

Найдем значения констант a, b, c, для которых истинны следующие предложения:

a + b = c

a > 0

b > 0

c > 0

Чтобы ввести эту задачу в SMT решатель, нужно перевести её на язык, который он может обработать. Существует инициатива SMT-LIB, которая нацелена на создание стандартного языка, которым могут пользоваться множество разных SMT решателей. В этих примерах мы будем использовать язык SMT-LIB.

На этом языке условие задачи запишется так:

(declare-fun a () Int)

(declare-fun b () Int)

(declare-fun c () Int)

(assert (> a 0))

(assert (> b 0))

(assert (> c 0))

(assert (= (+ a b) c))

(check-sat)

(get-model)

Этот текст содержит 3 компонента: объявление констант, задание формул, команды «проверить формулы на выполнимость» и «получить модель».

Текст задачи нужно передать SMT-решателю. В документации конкретного решателя вы найдете, как это делается. Выше есть ссылка на веб-интерфейс к z3. Если же вы хотите запустить z3 на своей машине, нужно загрузить билд отсюда: https://github.com/Z3Prover/z3/releases, или собрать его из исходников.

z3 выдает результат:

sat

(model

  (define-fun b () Int 1)

  (define-fun a () Int 1)

  (define-fun c () Int 2)

)

sat означает, что набор формул в условии задачи является выполнимым.

a, b и с это константы. Константы в описании задачи объявлены без значений, константы в модели определены со значениями. Константа по сути это нульарная функция, поэтому в синтаксисе SMT-LIB константы определяются как нульарные функции. Есть синтаксический сахар, который маскирует нульарную функцию под константу, можете погуглить синтаксис.

Невыполнимая задача

Попробуем найти решение уравнения a = a + 1

(declare-fun a () Int)

(assert (= (+ a 1) a))

(check-sat)

Программа выдаст результат: unsat. Это значит, что набор формул невыполним в обыкновенных целых числах, решений уравнения нет.

Продвинутый пример

Давайте попробуем перечислить все нестрого возрастающие последовательности 4х натуральных чисел от 1 до 4.

Например: (1, 2, 3, 4), (1, 1, 2, 2), (1, 1, 1, 1) и так далее.

Заведем 4 константы:

a1, a2, a3, a4.

(declare-fun a1 () Int)

(declare-fun a2 () Int)

(declare-fun a3 () Int)

(declare-fun a4 () Int)

Зададим условие нестрогого возрастания последовательности 4х чисел:

a1 ≤ a2

a2 ≤ a3

a3 ≤ a4

(assert (<= a1 a2))

(assert (<= a2 a3))

(assert (<= a3 a4))

Добавим еще команды

(check-sat)

(get-model)

SMT-решатель выведет какое-нибудь из решений:

(0, 0, 0, 0)

Чтобы найти следующий результат, нужно в условие задачи дописать такой assertion:

(a1, a2, a3, a4) != (0, 0, 0, 0)

Теперь SMT-решатель выведет что-то новое, например

(1, 1, 2, 2)

Чтобы найти следующий результат, нужно добавить еще один assertion:

 (a1, a2, a3, a4) != (1, 1, 2, 2)

Все ограничения на языке SMT-LIB будут выглядеть так:

(assert (<= a1 a2))

(assert (<= a2 a3))

(assert (<= a3 a4))

(assert (not (and (= a1 0) (= a2 0) (= a3 0) (= a4 0)))

(assert (not (and (= a1 1) (= a2 1) (= a3 2) (= a4 2)))

И так далее. Этот прием позволит вам перебрать наборы констант (моделей), для которых истинно формулы ограничений.

Вот программа на питоне, которая реализует этот принцип: https://gist.github.com/vzhn/62d46328a2566aecce097d2b6348355e

Совет: если будете запускать эту программу через IntelliJ PyCharm, не устанавливайте автоматически пакет z3. Установите вручную другой пакет: «z3-solver», вот так:

File -> Settings -> Project -> Python Interpreter -> + -> Add package "z3-solver.”

Грамматики

Не буду здесь подробно описывать, что это такое. Если вы не знакомы с формальными грамматиками, можете начать со статьи в Википедии: https://ru.wikipedia.org/wiki/Формальная_грамматика.

Примем следующее соглашение. Правила формальной грамматики будут состоять из правил двух типов: правила-суммы (Σ) и правила-произведения (Π). Любую контекстно-свободную грамматику можно привести к такому формату.

Грамматика лямбда-исчисления

В качестве примера мы будем здесь рассматривать грамматику лямбда-исчисления.

Алфавит: ‘λ’, ‘.’, ’a’, ‘b’, ‘c’, T, V, App, Abst

Терминальные символы: ‘λ’, ‘.’, ’a’, ‘b’, ‘c’

Нетерминальные символы: T, V, App, Abst

Правила:

T = V | App | Abst

V = a | b | c

App = T T

Abst = λ V. T

Правила-суммы

Грамматика содержит правила, по которым одни символы могут «раскрываться» в другие.

Например, рассмотрим правило для нетерминала T:

T = V | App | Abst

Это правило-сумма: нетерминал T раскрывается либо в символ V, либо в App, либо в Abst.

Попробую провести аналогию: представьте, что T это ящик, в котором находится один и только один другой ящик: либо V, либо App, либо Abst:

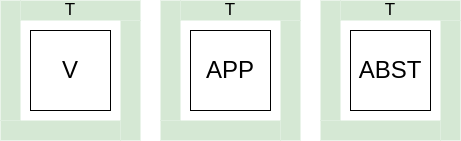
Правила-произведения

Рассмотрим правило Abst. 

Abst = λ V. T

Нетерминал Abst раскрывается в строку, которая состоит из символов, следующих один за другим:»λ», V,».«и T.

Можно представить, что правило-произведение это такой ящик, в котором находятся другие ящики, один за другим.

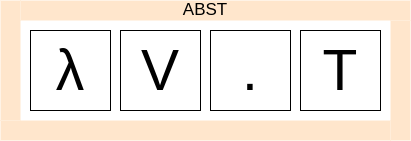
Когда мы раскрываем ящик Abst, мы достаем оттуда последовательно ящики «λ» V ».» и T. Вот что такое правило-произведение.

Грамматический вывод

Если мы применяем правила последовательно до тех пор, пока еще есть возможность это делать, формируется цепочка преобразований строк. Например, такая:

T ⟶ ABST⟶ λ V. T ⟶ λ a. APP ⟶ λ a. T T ⟶ λ a. V V ⟶ λ a. b c

Или такая:

λ a. b c ⟶ λ a. V V ⟶ λ a. T T ⟶ λ a. APP ⟶ λ V. T ⟶ ABST ⟶ T

Конечно, в грамматике не должно быть циклов, допускающих разборы бесконечной длины. Такие грамматики практически бесполезны, не будем здесь их рассматривать.

Первую цепочку генерирует разбор «сверху вниз». Вторую — разбор «снизу вверх».

Эту цепочку преобразований можно представить в виде такого рисунка:

наглядное представление грамматического вывода

В первой строке сверху единственный нетерминал Т. Он широкий, потому что транзитивно содержит 5 терминальных символов.

По выводу можно однозначно построить такую таблицу, и наоборот, по такой таблице можно однозначно восстановить грамматический вывод. Утверждение сильное, но доказывать его мы не будем.

SMT

Чтобы решить нашу задачу с помощью SMT решателя, ее нужно сформулировать на языке логики предикатов. Для нашей простой задачи ни кванторы, ни неинтерпретируемые функции не нужны, это упрощает задачу. Каждой клетке таблицы сопоставим набор чисел, кодирующий состояние этой ячейки. Состояние ячейки не может быть произвольным: иначе по таблице не получится восстановить корректный вывод. Сначала мы заведем таблицу с переменными, а потом установим ограничения на значения этих переменных. Итак, поехали!

Таблица

Состоит из строк и колонок. В каждой ячейке будут находиться 5 целочисленных констант, которые мы определим ниже. Количество колонок соответствует количеству символов в строке, которую нужно разобрать. Количество строк зависит от грамматики: если грамматика не допускает вывод бесконечной длины, то количество строк варьируется в некотором диапазоне. Этот диапазон вычисляется с помощью специального алгоритма. Задача интересная, но здесь её рассматривать не будем.

Символы

Каждой ячейке соответствует какой-то символ грамматики. Первая строка (нижняя) это начало разбора, поэтому в ней должны быть терминальные символы. Последняя (верхняя) строка таблицы соответствует единственному нетерминальному символу: цели разбора. Строки будем нумеровать снизу вверх, а колонки — слева направо.

Зеленые — суммы, оранжевые — произведения, синие — терминалы

Группа

Добавим признак, по которому можно будет определить, соответствуют соседние ячейки одному и тому же символу грамматики, или же разным, но возможно, одноименным. Назовем этот признак «Группа» (GroupId). Посмотрите на рисунок: на верхней строке таблицы ячейки » T T T T T» принадлежат одной группе, а на третьей строке (снизу) ячейки «T T» принадлежат разным группам: 3 и 4. 

каждая «полочка» это группа

Индекс

Будет полезно также ввести порядковый номер ячейки в группе. Индекс начинается с нуля и монотонно возрастает в пределах группы. Например, если в группе 3 ячейки, то индекс первой будет 0, индекс второй будет 1, а индекс последней: 2. Индекс первой ячейки в следующей группе снова будет 0, и так далее.

фиолетовая полочка это индекс

Тип продукции

Если символ ячейки в текущей строке отличается от символа ячейки в предыдущей (нижней) строке, то это значит, что происходит продукция: символ грамматики заменяется на другой символ грамматики в соответствии с правилами. Если символы в вертикально-смежных ячейках не отличаются, то продукции не происходит. Такие символы будут далее обозначаться серым цветом. Внимательный читатель может заметить, что во второй колонке продукция a ⟶ V может происходить в разных местах: на 2, 3, 4 или 5 строке. Это создает некоторую неопределенность, мы вернемся к этой проблеме позже.

зеленые — суммы, оранжевые — произведения, серые — «холостые» продукции

Подгруппа

Эта константа используется только для П-правил. Каждая подгруппа соответствует символу П-правила. То есть «целая» группа соответствует символу целиком, а подгруппы — его компонентам.

Например, в правиле

APP = T T 

Есть 2 компоненты: T и T.

Для этих компонент мы заведем 2 подгруппы, для первого символа T, и для второго.

Нужно проконтролировать, что символы в ячейках следуют точно в том количестве и порядке, в котором перечислены символы в правиле.

красные полочки это компоненты П-правила

Итоги

Таким образом мы получили, что каждой клеточке соответствует набор из 5 констант:

• Символ грамматики: SymbolId

• Группа: GroupId

• Тип продукции: Σ (1), П (2), или «пропуск»(0): ProductionTypeId

• Подгруппа: SubGroupId

• Порядковый номер ячейки в группе: Index

Формулы

Базовые принципы

Диапазоны

В каждой ячейке находятся 5 констант. Определим допустимые диапазоны значений каждого числа:

0 <= SymbolId < количество символов в грамматике, терминальных и нетерминальных

0 <= GroupId < количество колонок

0 <= SubGroupId < количество колонок

0 <= Index < количество колонок

0 <= ProdTypeId < 2

ProdTypeId принимает одно из 3х значений: пропуск (0), Σ (1), П (2)

Количество колонок равно количеству терминальных символов в строке, которую нужно разобрать.

Первая колонка

В первой колонке находится первая ячейка первой группы.

GroupId = 0; SubGroupId = 0; Index = 0

Первая строка

Формируется из исходной строки, которую нужно распарсить. Каждая группа в первой строке содержит только один символ. Этот символ всегда терминальный, потому что исходная строка состоит из терминалов.

GroupId = 0; SymbolId = {идентификатор терминального символа}

Строки, кроме первой

Мы хотим, чтобы в каждой строке была как минимум одна продукция. Поэтому хотя бы для одной ячейки ProdTypeId не должно быть равно значению «пропуск»(0).

Группы

Смежные группы

Для каждой пары соседних ячеек в строке значения GroupId должны быть либо равны, либо GroupId правой должен быть больше на единицу, чем GroupId левой. Если же GroupId равны, то эти ячейки принадлежат одной группе и одному правилу.

в красной рамке GroupId смежных ячеек отличаются больше, чем на единицу

Смежные подгруппы

Здесь принцип похожий: SubGroupId соседних ячеек, которые принадлежат одной группе, должны начинаться с нуля и не должны отличаться больше, чем на единицу.

в красной рамке SubGroupId смежных ячеек отличаются больше, чем на единицу

Индексы соседних ячеек

В пределах одной группы номера ячеек должны начинаться с нуля и монотонно возрастать.

В красной рамке номера ячеек или не возрастают, или возрастают немонотонно

Не разделяем группы

Группы по мере продвижения «вверх» могут только укрупняться. Если в строке есть «стык» между группами, то в нижней строке на том же месте тоже должен быть стык между группами.

В красной рамке конфигурация, которая не может быть разбором

Все ячейки в группе принадлежат одному нетерминалу

Группа содержит ячейки, сгруппированные по нетерминальному символу. Поэтому в группе все ячейки должны принадлежать одному нетерминалу.

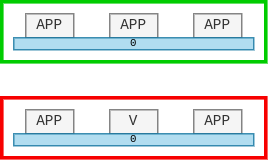нетерминал V выбивается из группы

Все ячейки в группе принадлежат одному типу продукции

В красной рамке первая ячейка П, а две другие Σ

Зависимость номера подгруппы от типа продукции

Подгруппы используются только в Π-правилах, поэтому для определенности пусть для остальных правил номер подгруппы всегда будет 0.

Зависимость номера подгруппы от номера группы

Номер подгруппы связан с номером группы ячейки в нижнем ряду. Если в рамках текущей группы соседние ячейки принадлежат одной и той же подгруппе, значит в нижнем ряду ячейки должны принадлежать одной и той же группе. Звучит запутанно, но попробуйте понять это по картинке: длина и количество красных полочек должны совпадать с длиной и количеством синих полочек в строке ниже. Номера могут и не совпадать.

Холостые продукции

Если ячейка не участвует в продукции, то символ в текущей ячейке должен совпадать с символом в нижней ячейке. Назовем такую «продукцию» холостой.

Положение холостых продукций

Наличие «холостых» ячеек допускает некоторую вариативность в том, на какой строке может находиться продукция. На картинке ниже мы видим, что продукция a ⟶ V может находиться на разных строках. Для определенности мы отбросим все случаи, в которых «холостые» ячейки находятся между продукциями.

В колонке, которая в зеленой рамке, продукция V находится так высоко, как это возможно.

Σ-правила

Если ProductionTypeId это «Сумма», то SymbolId должен соответствовать правилу-сумме.

Π-правила

Первый символ в группе должен соответствовать первому компоненту Π-правила. Символ является первым в группе, если он находится в первой колонке, либо находится на стыке разных групп в правой группе. На картинке ниже изображен первый кейс. 

Аналогично последний символ в группе должен соответствовать последнему компоненту Π-правила.

Если символов больше 2х, то нужны правила для переходов: между первым и вторым компонентом, между вторым и третьим, и между третьим и четвертым:

Если SubGroupId смежных ячеек различается, значит GroupId смежных ячеек в нижней строке тоже должны различаться и SymbolId должны соответствовать символам смежных компонент. Звучит запутанно, но работает.

Цель

Разбор успешен, когда все ячейки в последней строчке находятся в одной группе, то есть соответствуют одному нетерминальному символу. И если для этого символа больше нет продукций.

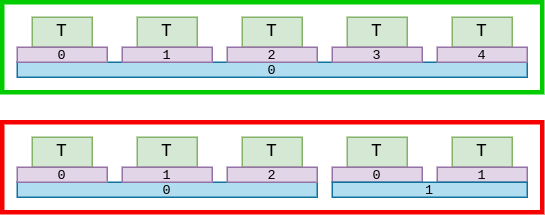Символ T в первой сроке не входит ни в одно правило-сумму. Разбор окончен. Символы T T во второй строчке являются продукцией правила App. Разбор не окончен.

Программа

Эти идеи реализованы в программе https://github.com/vzhn/z3-parser. Инструкции по запуску и сборке представлены там же. Программа написана на языке kotlin, для взаимодействия с z3 используется обертка com.microsoft:z3:4.8.17

Что не вошло в пост

Похожие принципы можно использовать, чтобы порождать строки по грамматике. Еще можно заполнять пропуски: задаем часть строки, чтобы программа нашла все варианты, которые подходят под грамматику. Это трудно сделать классическим путем, с помощью программирования, но относительно несложно с помощью SMT-решателя.

Открытый вопрос

Значительную часть поста составляют логические выражения, описывающие отношения между значениями в соседних ячейках таблицы. Можно ли вывести эти формулы с помощью алгоритма?

Итоги

SMT-решатели это чрезвычайно мощный и интересный инструмент. В каком-то смысле он реализует идею no-code: вместо написания программы можно перевести задачу в логические предложения, передать их в решатель, и надеяться получить ответ.

С помощью SMT-решателей также можно решать головоломки: судоку, сокобан и другие. Можно составлять расписания задач (critical path method) для составления диаграммы Гантта и многое, многое другое. Заинтереснованным могу порекомендовать книгу: SAT/SMT by Example by Dennis Yurichev.

Если вы жаждете строгих математических определений, загляните в учебники по математической логике. Вам пригодится логика высказываний, логика предикатов (она же логика первого порядка), понятия алгебраических систем, истинности на алгебраических системах и основы теории моделей. Я пользуюсь учебником »Математическая логика,  Ершов Ю.Л.,  Палютин Е.А.», но не могу сказать, что он лучший.

© Habrahabr.ru