Открытый курс машинного обучения. Тема 3. Классификация, деревья решений и метод ближайших соседей13.03.2017 14:18

Привет всем, кто проходит курс машинного обучения на Хабре!

В первых двух частях (1, 2) мы попрактиковались в первичном анализе данных с Pandas и в построении картинок, позволяющих делать выводы по данным. Сегодня наконец перейдем к машинному обучению. Поговорим о задачах машинного обучения и рассмотрим 2 простых подхода — деревья решений и метод ближайших соседей. Также обсудим, как с помощью кросс-валидации выбирать модель для конкретных данных.

Напомним, что к курсу еще можно подключиться, дедлайн по 2 домашнему заданию — 13 марта 23:59.

Список статей серии

Первичный анализ данных с Pandas
Визуальный анализ данных c Python
Классификация, деревья решений и метод ближайших соседей
Линейные модели классификации и регрессии. Кросс-валидация и оценка модели
Композиции: бэггинг, случайный лес. Кривые валидации и обучения
Обучение без учителя: PCA, кластеризация, поиск аномалий
Искусство построения и отбора признаков. Приложения в задачах обработки текста, изображений и гео-данных

План этой статьи:

Введение
Дерево решений
- Как строится дерево решений
- Как дерево решений работает с количественными признаками
- Основные параметры дерева
- Дерево решений в задаче регрессии
Метод ближайших соседей
- Метод ближайших соседей в реальных задачах
- Класс KNeighborsClassifier в Scikit-learn
Выбор параметров модели и кросс-валидация
Примеры применения
- Деревья решений и метод ближайших соседей в задаче прогнозирования оттока клиентов телеком-оператора
- Сложный случай для деревьев решений
- Деревья решений и метод ближайших соседей в задаче распознавания рукописных цифр MNIST
- Сложный случай для метода ближайших соседей
Плюсы и минусы деревьев решений и метода ближайших соседей
Домашнее задание №3
Обзор ресурсов

Введение

Наверно хочется сразу рвануть в бой, но сначала поговорим про то, какую именно задачу будем решать и каково ее место в области машинного обучения.
Классическое, общее (и не больно то строгое) определение машинного обучения звучит так (T. Mitchell «Machine learning», 1997):

говорят, что компьютерная программа обучается при решении какой-то задачи из класса T, если ее производительность, согласно метрике P, улучшается при накоплении опыта E.

Далее в разных сценариях под T, P, и E подразумеваются совершенно разные вещи. Среди самых популярных задач T в машинном обучении:

классификация — отнесение объекта к одной из категорий на основании его признаков
регрессия — прогнозирование количественного признака объекта на основании прочих его признаков
кластеризация — разбиение множества объектов на группы на основании признаков этих объектов так, чтобы внутри групп объекты были похожи между собой, а вне одной группы — менее похожи
детекция аномалий — поиск объектов, «сильно непохожих» на все остальные в выборке либо на какую-то группу объектов
и много других, более специфичных. Хороший обзор дан в главе «Machine Learning basics» книги «Deep Learning» (Ian Goodfellow, Yoshua Bengio, Aaron Courville, 2016)

Под опытом E понимаются данные (без них никуда), и в зависимости от этого алгоритмы машинного обучения могут быть поделены на тех, что обучаются с учителем и без учителя (supervised & unsupervised learning). В задачах обучения без учителя имеется выборка, состоящая из объектов, описываемых набором признаков. В задачах обучения с учителем вдобавок к этому для каждого объекта некоторой выборки, называемой обучающей, известен целевой признак — по сути это то, что хотелось бы прогнозировать для прочих объектов, не из обучающей выборки.

Пример

Задачи классификации и регрессии — это задачи обучения с учителем. В качестве примера будем представлять задачу кредитного скоринга: на основе накопленных банком данных о своих клиентах хочется прогнозировать невозврат кредита. Здесь для алгоритма опыт E — это имеющаяся обучающая выборка: набор объектов (людей), каждый из которых характеризуется набором признаков (таких как возраст, зарплата, тип кредита, невозвраты в прошлом и т.д.), а также целевым признаком. Если этот целевой признак — просто факт невозврата кредита (1 или 0, т.е. банк знает о своих клиентах, кто вернул кредит, а кто — нет), то это задача (бинарной) классификации. Если известно, на сколько по времени клиент затянул с возвратом кредита и хочется то же самое прогнозировать для новых клиентов, то это будет задачей регрессии.

Наконец, третья абстракция в определении машинного обучения — это метрика оценки производительности алгоритма P. Такие метрики различаются для разных задач и алгоритмов, и про них мы будим говорить по мере изучения алгоритмов. Пока скажем, что самая простая метрика качества алгоритма, решающего задачу классификации — это доля правильных ответов (accuracy, не называйте ее точностью, этот перевод зарезервирован под другую метрику, precision) — то есть попросту доля верных прогнозов алгоритма на тестовой выборке.

Далее будем говорить о двух задачах обучения с учителем: о классификации и регресcии.

Дерево решений

Начнем обзор методов классификации и регрессии с одного из самых популярных — с дерева решений. Деревья решений используются в повседневной жизни в самых разных областях человеческой деятельности, порой и очень далеких от машинного обучения. Деревом решений можно назвать наглядную инструкцию, что делать в какой ситуации. Приведем пример из области консультирования научных сотрудников института. Высшая Школа Экономики выпускает инфо-схемы, облегчающие жизнь своим сотрудникам. Вот фрагмент инструкции по публикации научной статьи на портале института.

В терминах машинного обучения можно сказать, что это элементарный классификатор, который определяет форму публикации на портале (книга, статья, глава книги, препринт, публикация в «НИУ ВШЭ и СМИ») по нескольким признакам: типу публикации (монография, брошюра, статья и т.д.), типу издания, где опубликована статья (научный журнал, сборник трудов и т.д.) и остальным.

Зачастую дерево решений служит обобщением опыта экспертов, средством передачи знаний будущим сотрудникам или моделью бизнес-процесса компании. Например, до внедрения масштабируемых алгоритмов машинного обучения в банковской сфере задача кредитного скоринга решалась экспертами. Решение о выдаче кредита заемщику принималось на основе некоторых интуитивно (или по опыту) выведенных правил, которые можно представить в виде дерева решений.

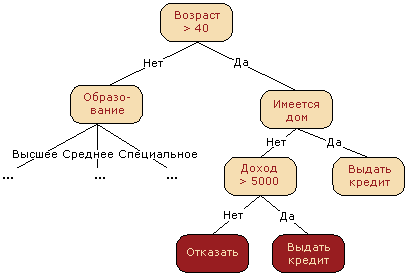
В этом случае можно сказать, что решается задача бинарной классификации (целевой класс имеет два значения: «Выдать кредит» и «Отказать») по признакам «Возраст», «Наличие дома», «Доход» и «Образование».

Дерево решений как алгоритм машинного обучения — по сути то же самое: объединение логических правил вида «Значение признака $a$ меньше $x$ И Значение признака $b$ меньше $y$ … => Класс 1» в структуру данных «Дерево». Огромное преимущество деревьев решений в том, что они легко интерпретируемы, понятны человеку. Например, по схеме на рисунке выше можно объяснить заемщику, почему ему было отказано в кредите. Скажем, потому, что у него нет дома и доход меньше 5000. Как мы увидим дальше, многие другие, хоть и более точные, модели не обладают этим свойством и могут рассматриваться скорее как «черный ящик», в который загрузили данные и получили ответ. В связи с этой «понятностью» деревьев решений и их сходством с моделью принятия решений человеком (можно легко объяснять боссу свою модель), деревья решений получили огромную популярность, а один из представителей этой группы методов классификации, С4.5, рассматривается первым в списке 10 лучших алгоритмов интеллектуального анализа данных («Top 10 algorithms in data mining», Knowledge and Information Systems, 2008. PDF).

Как строится дерево решений

В примере с кредитным скорингом мы видели, что решение о выдаче кредита принималось на основе возраста, наличия недвижимости, дохода и других. Но какой признак выбрать первым? Для этого рассмотрим пример попроще, где все признаки бинарные.

Здесь можно вспомнить игру »20 вопросов», которая часто упоминается во введении в деревья решений. Наверняка каждый в нее играл. Один человек загадывает знаменитость, а второй пытается отгадать, задавая только вопросы, на которые можно ответить «Да» или «Нет» (опустим варианты «не знаю» и «не могу сказать»). Какой вопрос отгадывающий задаст первым делом? Конечно, такой, который сильнее всего уменьшит количество оставшихся вариантов. К примеру, вопрос «Это Анджелина Джоли?» в случае отрицательного ответа оставит более 6 миллиардов вариантов для дальнейшего перебора (конечно, поменьше, не каждый человек — знаменитость, но все равно немало), а вот вопрос «Это женщина?» отсечет уже около половины знаменитостей. То есть, признак «пол» намного лучше разделяет выборку людей, чем признак «это Анджелина Джоли», «национальность-испанец» или «любит футбол». Это интуитивно соответствует понятию прироста информации, основанного на энтропии.

Энтропия

Энтропия Шеннона определяется для системы с $N$ возможными состояниями следующим образом:

$\Large S = -\sum_{i=1}^{N}p_ilog_2p_i,$

где $p_i$ — вероятности нахождения системы в $i$ -ом состоянии. Это очень важное понятие, используемое в физике, теории информации и других областях. Опуская предпосылки введения (комбинаторные и теоретико-информационные) этого понятия, отметим, что, интуитивно, энтропия соответствует степени хаоса в системе. Чем выше энтропия, тем менее упорядочена система и наоборот. Это поможет там формализовать «эффективное разделение выборки», про которое мы говорили в контексте игры »20 вопросов».

Пример

Для иллюстрации того, как энтропия поможет определить хорошие признаки для построения дерева, приведем тот же игрушечный пример, что в статье «Энтропия и деревья принятия решений». Будем предсказывать цвет шарика по его координате. Конечно, ничего общего с жизнью это не имеет, но позволяет показать, как энтропия используется для построения дерева решений.

Здесь 9 синих шариков и 11 желтых. Если мы наудачу вытащили шарик, то он с вероятностью $p_1=\frac{9}{20}$ будет синим и с вероятностью $p_2=\frac{11}{20}$ — желтым. Значит, энтропия состояния $S_0 = -\frac{9}{20}log_2{\frac{9}{20}}-\frac{11}{20}log_2{\frac{11}{20}} \approx 1$ . Само это значение пока ни о чем нам не говорит. Теперь посмотрим, как изменится энтропия, если разбить шарики на две группы — с координатой меньше либо равной 12 и больше 12.

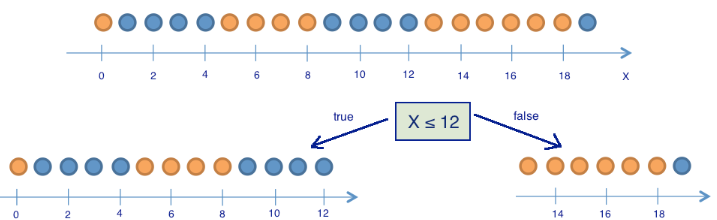
В левой группе оказалось 13 шаров, из которых 8 синих и 5 желтых. Энтропия этой группы равна $S_1 = -\frac{5}{13}log_2{\frac{5}{13}}-\frac{8}{13}log_2{\frac{8}{13}} \approx 0.96$ . В правой группе оказалось 7 шаров, из которых 1 синий и 6 желтых. Энтропия правой группы равна $S_2 = -\frac{1}{7}log_2{\frac{1}{7}}-\frac{6}{7}log_2{\frac{6}{7}} \approx 0.6$ . Как видим, энтропия уменьшилась в обеих группах по сравнению с начальным состоянием, хоть в левой и не сильно. Поскольку энтропия — по сути степень хаоса (или неопределенности) в системе, уменьшение энтропии называют приростом информации. Формально прирост информации (information gain, IG) при разбиении выборки по признаку $Q$ (в нашем примере это признак » $x \leq 12$ ») определяется как

$\Large IG(Q) = S_O - \sum_{i=1}^{q}\frac{|N_i|}{N}S_i,$

где $q$ — число групп после разбиения, $N_i$ — число элементов выборки, у которых признак $Q$ имеет $i$ -ое значение. В нашем случае после разделения получилось две группы ( $q = 2$ ) — одна из 13 элементов ( $N_1 = 13$ ), вторая — из 7 ( $N_2 = 7$ ). Прирост информации получился

$\Large IG(x \leq 12) = S_0 - \frac{13}{20}S_1 - \frac{7}{20}S_2 \approx 0.16.$

Получается, разделив шарики на две группы по признаку «координата меньше либо равна 12», мы уже получили более упорядоченную систему, чем в начале. Продолжим деление шариков на группы до тех пор, пока в каждой группе шарики не будут одного цвета.

Для правой группы потребовалось всего одно дополнительное разбиение по признаку «координата меньше либо равна 18», для левой — еще три. Очевидно, энтропия группы с шариками одного цвета равна 0 ( $log_2{1} = 0$ ), что соответствует представлению, что группа шариков одного цвета — упорядоченная.
В итоге мы построили дерево решений, предсказывающее цвет шарика по его координате. Отметим, что такое дерево решений может плохо работать для новых объектов (определения цвета новых шариков), поскольку оно идеально подстроилось под обучающую выборку (изначальные 20 шариков). Для классификации новых шариков лучше подойдет дерево с меньшим числом «вопросов», или разделений, пусть даже оно и не идеально разбивает по цветам обучающую выборку. Эту проблему, переобучение, мы еще рассмотрим далее.

Алгоритм построения дерева

Можно убедиться в том, что построенное в предыдущем примере дерево является в некотором смысле оптимальным — потребовалось только 5 «вопросов» (условий на признак $x$ ), чтобы «подогнать» дерево решений под обучающую выборку, то есть чтобы дерево правильно классифицировало любой обучающий объект. При других условиях разделения выборки дерево получится глубже.

В основе популярных алгоритмов построения дерева решений, таких как ID3 и C4.5, лежит принцип жадной максимизации прироста информации — на каждом шаге выбирается тот признак, при разделении по которому прирост информации оказывается наибольшим. Дальше процедура повторяется рекурсивно, пока энтропия не окажется равной нулю или какой-то малой величине (если дерево не подгоняется идеально под обучающую выборку во избежание переобучения).
В разных алгоритмах применяются разные эвристики для «ранней остановки» или «отсечения», чтобы избежать построения переобученного дерева.

def build(L):
    create node t
    if the stopping criterion is True:
        assign a predictive model to t
    else:
        Find the best binary split L = L_left + L_right
        t.left = build(L_left)
        t.right = build(L_right)
    return t

Другие критерии качества разбиения в задаче классификации

Мы разобрались, в том, как понятие энтропии позволяет формализовать представление о качестве разбиения в дереве. Но это всего-лишь эвристика, существуют и другие:

Неопределенность Джини (Gini impurity): $G = 1 - \sum\limits_k (p_k)^2$ . Максимизацию этого критерия можно интерпретировать как максимизацию числа пар объектов одного класса, оказавшихся в одном поддереве. Подробнее об этом (как и обо многом другом) можно узнать из репозитория Евгения Соколова. Не путать с индексом Джини! Подробнее об этой путанице — в блогпосте Александра Дьяконова
Ошибка классификации (misclassification error): $E = 1 - \max\limits_k p_k$

На практике ошибка классификации почти не используется, а неопределенность Джини и прирост информации работают почти одинаково.

В случае задачи бинарной классификации ( $p_+$ — вероятность объекта иметь метку +) энтропия и неопределенность Джини примут следующий вид:

$S = -p_+ \log_2{p_+} -p_- \log_2{p_-} = -p_+ \log_2{p_+} -(1 - p_{+}) \log_2{(1 - p_{+})};$

$ G = 1 - p_+^2 - p_-^2 = 1 - p_+^2 - (1 - p_+)^2 = 2p_+(1-p_+).$

Когда мы построим графики этух двух функций от аргумента $p_+$ , то увидим, что график энтропии очень близок к графику удвоенной неопределенности Джини, и поэтому на практике эти два критерия «работают» почти одинаково.

Импорт библиотек

from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import pylab as plt
%matplotlib inline
import seaborn as sns
from matplotlib import pyplot as plt

Отрисовка картинки

plt.rcParams['figure.figsize'] = (6,4)
xx = np.linspace(0,1,50)
plt.plot(xx, [2 * x * (1-x) for x in xx], label='gini')
plt.plot(xx, [4 * x * (1-x) for x in xx], label='2*gini')
plt.plot(xx, [-x * np.log2(x) - (1-x) * np.log2(1 - x)  for x in xx], label='entropy')
plt.plot(xx, [1 - max(x, 1-x) for x in xx], label='missclass')
plt.plot(xx, [2 - 2 * max(x, 1-x) for x in xx], label='2*missclass')
plt.xlabel('p+')
plt.ylabel('criterion')
plt.title('Критерии качества как функции от p+ (бинарная классификация)')
plt.legend();

Пример

Рассмотрим пример применения дерева решений из библиотеки Scikit-learn для синтетических данных. Два класса будут сгенерированы из двух нормальных распределений с разными средними.

Код для генерации данных

# первый класс
np.seed = 7
train_data = np.random.normal(size=(100, 2))
train_labels = np.zeros(100)

# добавляем второй класс
train_data = np.r_[train_data, np.random.normal(size=(100, 2), loc=2)]
train_labels = np.r_[train_labels, np.ones(100)]

Отобразим данные. Неформально, задача классификации в этом случае — построить какую-то «хорошую» границу, разделяющую 2 класса (красные точки от желтых). Если утрировать, то машинное обучение в этом случае сводится к тому, как выбрать хорошую разделяющую границу. Возможно, прямая будет слишком простой границей, а какая-то сложная кривая, огибающая каждую красную точку — будет слишком сложной и будем много ошибаться на новых примерах из того же распределения, из которого пришла обучающая выборка. Интуиция подсказывает, что хорошо на новых данных будет работать какая-то гладкая граница, разделяющая 2 класса, или хотя бы просто прямая (в $n$ -мерном случае — гиперплоскость).

Отрисовка картинки


plt.rcParams['figure.figsize'] = (10,8)
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, 
cmap='autumn', edgecolors='black', linewidth=1.5);
plt.plot(range(-2,5), range(4,-3,-1));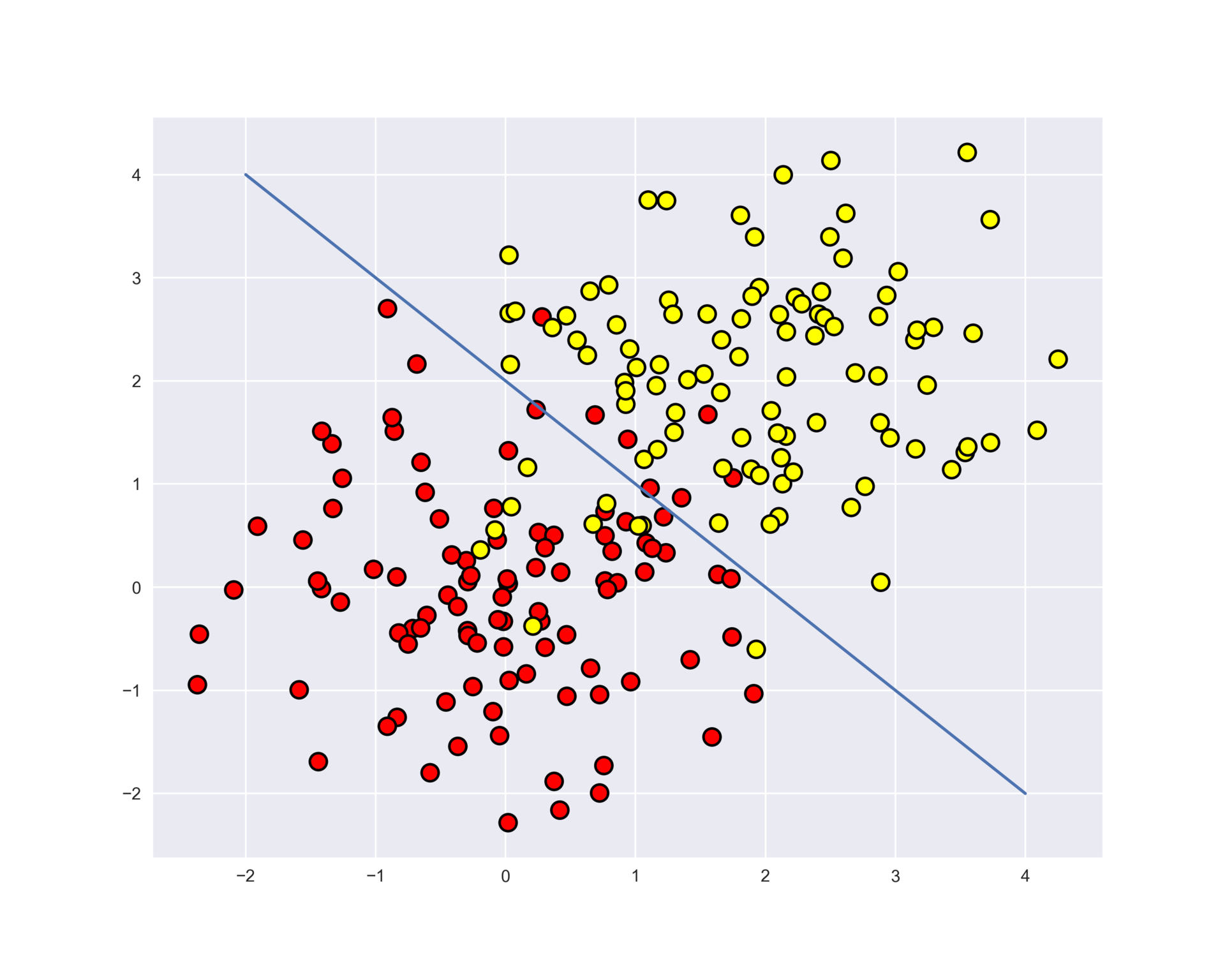

Попробуем разделить эти два класса, обучив дерево решений. В дереве будем использовать параметр max_depth, ограничивающий глубину дерева. Визуализируем полученную границу разделения класссов.

Код для обучения дерева и отрисовки его разделяющей границы

from sklearn.tree import DecisionTreeClassifier

# Напишем вспомогательную функцию, которая будет возвращать решетку для дальнейшей визуализации.
def get_grid(data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
return np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

# параметр min_samples_leaf указывает, при каком минимальном количестве
# элементов в узле он будет дальше разделяться
clf_tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=17)

# обучаем дерево
clf_tree.fit(train_data, train_labels)

# немного кода для отображения разделяющей поверхности
xx, yy = get_grid(train_data)
predicted = clf_tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, 
cmap='autumn', edgecolors='black', linewidth=1.5);

А как выглядит само построенное дерево? Видим, что дерево «нарезает» пространство на 7 прямоугольников (в дереве 7 листьев). В каждом таком прямоугольнике прогноз дерева будет константным, по превалированию объектов того или иного класса.

Код для отображения дерева

# используем .dot формат для визуализации дерева
from sklearn.tree import export_graphviz
export_graphviz(clf_tree, feature_names=['x1', 'x2'], 
out_file='../../img/small_tree.dot', filled=True)
# для этого понадобится библиотека pydot (pip install pydot)
!dot -Tpng '../../img/small_tree.dot' -o '../../img/small_tree.png'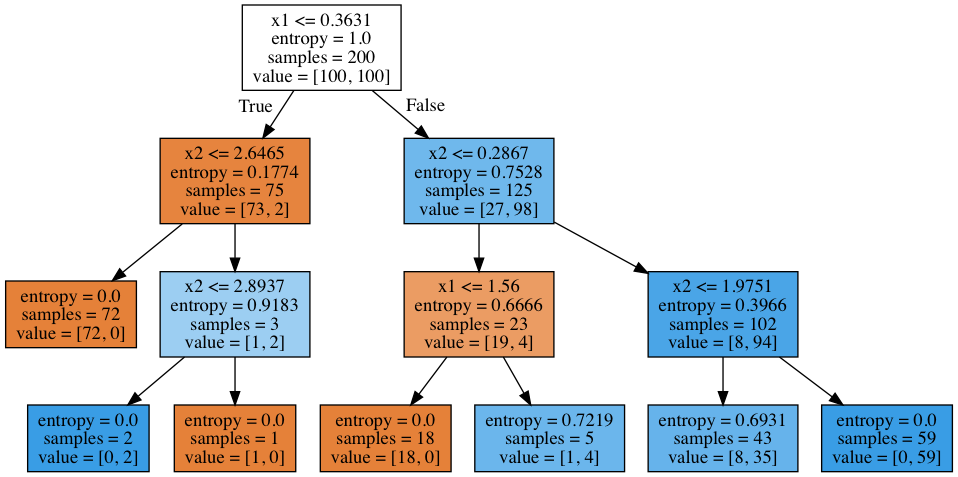

Как «читается» такое дерево?

В начале было 200 объектов, 100 — одного класса и 100 — другого. Энтропия начального состояния была максимальной — 1. Затем было сделано разбиение объектов на 2 группы в зависимости от сравнения признака $x_1$ со значением $0.3631$ (найдите этот участок границы на рисунке выше, до дерева). При этом энтропия и в левой, и в правой группе объектов уменьшилась. И так далее, дерево строится до глубины 3. При такой визуализации чем больше объектов одного класса, тем цвет вершины ближе к темно-оранжевому и, наоборот, чем больше объектов второго класса, тем ближе цвет к темно-синему. В начале объектов одного класса поровну, поэтому корневая вершина дерева — белого цвета.

Как дерево решений работает с количественными признаками

Допустим, в выборке имеется количественный признак «Возраст», имеющий много уникальных значений. Дерево решений будет искать лучшее (по критерию типа прироста информации) разбиение выборки, проверяя бинарные признаки типа «Возраст < 17", "Возраст < 22.87" и т.д. Но что если таких "нарезаний" возраста слишком много? А что если есть еще количественный признак "Зарплата", и зарплату тоже можно "нарезать" большим числом способов? Получается слишком много бинарных признаков для выбора лучшего на каждом шаге построения дерева. Для решения этой проблемы применяют эвристики для ограничения числа порогов, с которыми мы сравниваем количественный признак.

Рассмотрим это на игрушечном примере. Пусть имеется следующая выборка:

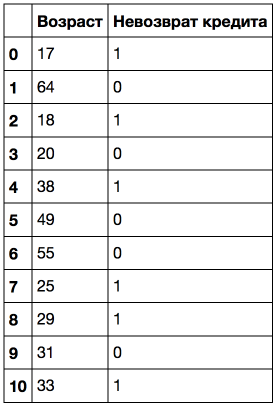
Отсортируем ее по возрастанию возраста.

Обучим на этих данных дерево решений (без ограничения глубины) и посмотрим на него.

Код для обучения и отрисовки дерева

age_tree = DecisionTreeClassifier(random_state=17)
age_tree.fit(data['Возраст'].values.reshape(-1, 1), data['Невозврат кредита'].values)

export_graphviz(age_tree, feature_names=['Возраст'], 
out_file='../../img/age_tree.dot', filled=True)
!dot -Tpng '../../img/age_tree.dot' -o '../../img/age_tree.png'

Видим, что дерево задействовало 5 значений, с которыми сравнивается возраст: 43.5, 19, 22.5, 30 и 32 года. Если приглядеться, то это аккурат средние значения между возрастами, при которых целевой класс «меняется» с 1 на 0 или наоборот. Сложная фраза, поэтому пример: 43.5 — это среднее между 38 и 49 годами, клиент, которому 38 лет не вернул кредит, а тот, которому 49 — вернул. Аналогично, 19 лет — среднее между 18 и 20 годами. То есть в качестве порогов для «нарезания» количественного признака, дерево «смотрит» на те значения, при которых целевой класс меняет свое значение.

Подумайте, почему не имеет смысла в данном случае рассматривать признак «Возраст < 17.5".

Рассмотрим пример посложнее: добавим признак «Зарплата» (тыс. рублей/месяц).

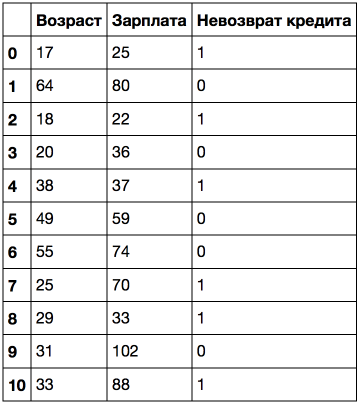
Если отсортировать по возрасту, то целевой класс («Невозврат кредита») меняется (с 1 на 0 или наоборот) 5 раз. А если отсортировать по зарплате — то 7 раз. Как теперь дерево будет выбирать признаки? Посмотрим.

Код для обучения и отрисовки дерева

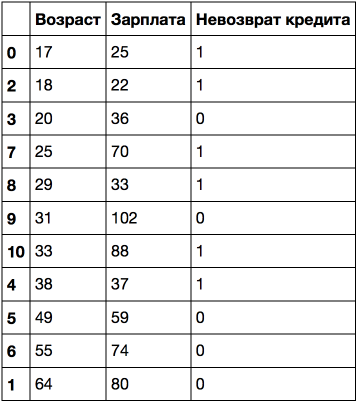
age_sal_tree = DecisionTreeClassifier(random_state=17)
age_sal_tree.fit(data2[['Возраст', 'Зарплата']].values, data2['Невозврат кредита'].values);

export_graphviz(age_sal_tree, feature_names=['Возраст', 'Зарплата'], 
out_file='../../img/age_sal_tree.dot', filled=True)
!dot -Tpng '../../img/age_sal_tree.dot' -o '../../img/age_sal_tree.png'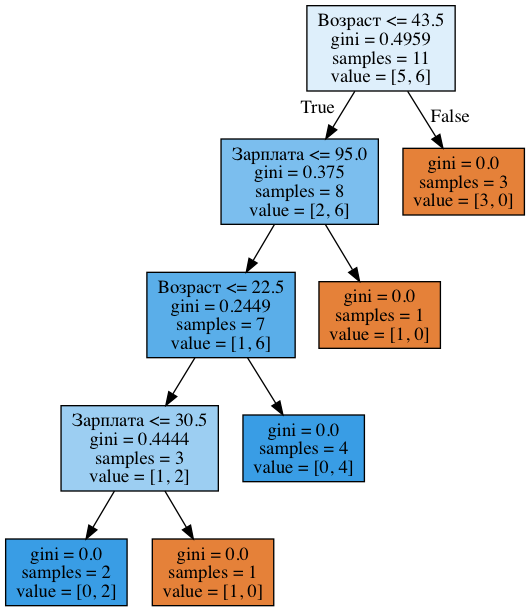

Видим, что в дереве задействованы как разбиения по возрасту, так и по зарплате. Причем пороги, с которыми сравниваются признаки: 43.5 и 22.5 года — для возраста и 95 и 30.5 тыс. руб/мес — для зарплаты. И опять можно заметить, что 95 тыс. — это среднее между 88 и 102, при этом человек с зарплатой 88 оказался «плохим», а с 102 — «хорошим». То же самое для 30.5 тыс. То есть перебирались сравнения зарплаты и возраста не со всеми возможными значениями, а только с несколькими. А почему в дереве оказались именно эти признаки? Потому что по ним разбиения оказались лучше (по критерию неопределенности Джини).

Вывод: самая простая эвристика для обработки количественных признаков в дереве решений: количественный признак сортируется по возрастанию, и в дереве проверяются только те пороги, при которых целевой признак меняет значение. Звучит не очень строго, но надеюсь, я донес смысл с помощью игрушечных примеров.

Дополнительно, когда в данных много количественных признаков, и у каждого много уникальных значений, могут отбираться не все пороги, описанные выше, а только топ-N, дающих максимальный прирост все того же критерия. То есть, по сути, для каждого порога строится дерево глубины 1, считается насколько снизилась энтропия (или неопределенность Джини) и выбираются только лучшие пороги, с которыми стоит сравнивать количественный признак.

Для иллюстрации: при разбиении по признаку «Зарплата $\leq$ 34.5» в левой подгруппе энтропия 0 (все клиенты «плохие»), а в правой — 0.954 (3 «плохих» и 5 «хороших», можете проверить, 1 часть домашнего задания будет как раз на то, чтоб разобраться досканально с построением деревьев). Прирост информации получается примерно 0.3.
А при разбиении по признаку «Зарплата $\leq$ 95» в левой подгруппе энтропия 0.97 (6 «плохих» и 4 «хороших»), а в правой — 0 (всего один объект). Прирост информации получается примерно 0.11.
Посчитав таким образом прирост информации для каждого разбиения, можно предварительно, до построения большого дерева (по всем признакам) отобрать пороги, с которыми будет сравниваться каждый количественный признак.

Еще примеры дискретизации количественных признаков можно посмотреть в постах, подобных этому или этому. Одна из самых известных научных статей на эту тему — «On the handling of continuous-valued attributes in decision tree generation» (U.M. Fayyad. K.B. Irani, «Machine Learning», 1992).

Основные параметры дерева

В принципе дерево решений можно построить до такой глубины, чтоб в каждом листе был ровно один объект. Но на практике это не делается (если строится только одно дерево) из-за того, что такое дерево будет переобученным — оно слишком настроится на обучающую выборку и будет плохо работать на прогноз на новых данных. Где-то внизу дерева, на большой глубине будут появляться разбиения по менее важным признакам (например, приехал ли клиент из Саратова или Костромы). Если утрировать, может оказаться так, что из всех 4 клиентов, пришедших в банк за кредитом в зеленых штанах, никто не вернул кредит. Но мы не хотим, чтобы наша модель классификации порождала такие специфичные правила.

Есть два исключения, ситуации, когда деревья строятся до максимальной глубины:

Случайный лес (композиция многих деревьев) усредняет ответы деревьев, построенных до максимальной глубины (почему стоит делать именно так, разберемся позже)
Стрижка дерева (pruning). При таком подходе дерево сначала строится до максимальной глубины, потом постепенно, снизу вверх, некоторые вершины дерева убираются за счет сравнения по качеству дерева с данным разбиением и без него (сравнение проводится с помощью кросс-валидации, о которой чуть ниже). Подробнее можно почитать в материалах репозитория Евгения Соколова.

Картинка ниже — пример разделяющей границы, построенной переобученным деревом.

Основные способы борьбы с переобучением в случае деревьев решений:

искусственное ограничение глубины или минимального числа объектов в листе: построение дерева просто в какой-то момент прекращается;
стрижка дерева

Класс DecisionTreeClassifier в Scikit-learn

Основные параметры класса sklearn.tree.DecisionTreeClassifier:

max_depth — максимальная глубина дерева
max_features — максимальное число признаков, по которым ищется лучшее разбиение в дереве (это нужно потому, что при большом количестве признаков будет «дорого» искать лучшее (по критерию типа прироста информации) разбиение среди всех признаков)
min_samples_leaf — минимальное число объектов в листе. У этого параметра есть понятная интерпретация: скажем, если он равен 5, то дерево будет порождать только те классифицирующие правила, которые верны как мимимум для 5 объектов

Параметры дерева надо настраивать в зависимости от входных данных, и делается это обычно с помощью кросс-валидации, про нее чуть ниже.

Дерево решений в задаче регрессии

При прогнозировании количественного признака идея построения дерева остается та же, но меняется критерий качества:

Дисперсия вокруг среднего: $\Large D = \frac{1}{\ell} \sum\limits_{i =1}^{\ell} (y_i - \frac{1}{\ell} \sum\limits_{i =1}^{\ell} y_i)^2,$
где $\ell$ — число объектов в листе, — значения целевого признака. Попросту говоря, минимизируя дисперсию вокруг среднего, мы ищем признаки, разбивающие выборку таким образом, что значения целевого признака в каждом листе примерно равны.

Пример

Сгенерируем данные, распределенные вокруг функции $f(x) = e^{-x ^ 2} + 1.5 * e^{-(x - 2) ^ 2}$ c некоторым шумом, обучим на них дерево решений и изобразим, какие прогнозы делает дерево.

Код

n_train = 150        
n_test = 1000       
noise = 0.1

def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)

def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2) + \
np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y

X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)

from sklearn.tree import DecisionTreeRegressor

reg_tree = DecisionTreeRegressor(max_depth=5, random_state=17)

reg_tree.fit(X_train, y_train)
reg_tree_pred = reg_tree.predict(X_test)

plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, reg_tree_pred, "g", lw=2)
plt.xlim([-5, 5])
plt.title("Decision tree regressor, MSE = %.2f" % np.sum((y_test - reg_tree_pred) ** 2))
plt.show()

Видим, что дерево решений аппроксимирует зависимость в данных кусочно-постоянной функцией.

Метод ближайших соседей

Метод ближайших соседей (k Nearest Neighbors, или kNN) — тоже очень популярный метод классификации, также иногда используемый в задачах регрессии. Это, наравне с деревом решений, один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей, какие преобладают, таков и ты. Формально основой метода является гипотезой компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.

Согласно методу ближайших соседей, тестовый пример (зеленый шарик) будет отнесен к классу «синие», а не «красные».

Например, если не знаешь, какой тип товара указать в объявлении для Bluetooth-гарнитуры, можешь найти 5 похожих гарнитур, и если 4 из них отнесены к категории «Аксессуары», и только один — к категории «Техника», то здравый смысл подскажет для своего объявления тоже указать категорию «Аксессуары».

Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:

Вычислить расстояние до каждого из объектов обучающей выборки
Отобрать объектов обучающей выборки, расстояние до которых минимально
Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди ближайших соседей

Под задачу регрессии метод адаптируется довольно легко — на 3 шаге возвращается не метка, а число — среднее (или медианное) значение целевого при