Описательная статистика перформанс-распределений

Нужна ли разработчику математика? Если анализировать замеры производительности, то матстатистика понадобится. Но оказывается, о ней нужно знать не совсем то, что в учебниках. А что тогда?
Андрей Акиньшин @DreamWalker поговорил об этом в докладе на нашей конференции Heisenbug. И теперь, пока мы готовим следующий Heisenbug (где тоже будут доклады о производительности), решили опубликовать текстовую версию его выступления (а для тех, кому удобнее видео, прикрепляем запись). Предупреждаем: много букв, цифр и графиков!
Содержание
Введение
Всем привет!
Меня зовут Андрей Акиньшин, и сегодня мы поговорим об описательной статистике перформанс-распределений.
В прошлой серии
Данная тема является продолжением моего прошлого доклада про перформанс-анализ, который я делал на конференции Heisenbug пару лет тому назад. Если вы еще не смотрели этот доклад, то обязательно посмотрите, а если смотрели, то давайте кратенько вспомним, о чем же шла речь.
Мы обсуждали тяжкую жизнь перформанс-инженера, который с утра до вечера решает перформанс-проблемы. Но стоит только разобраться с одной проблемой, сразу появляется другая, а за ней третья, четвертая и так далее.

Мы говорили о том, как же упростить жизнь нашего инженера и сделать процесс решения проблем более систематическим и контролируемым, а также по возможности сократить количество этих самых проблем.
Увы, серебряной пули тут не существует.
Потенциальное решение затрагивает множество аспектов разработки — от социально-менеджерских до инфраструктурно-девопсных. Но в центре такого решения находится набор инструментов, которые позволяют проводить надежные перформанс-исследования, писать стабильные перформанс-тесты, автоматически мониторить новые перформанс-проблемы и много чего еще. И для всех этих инструментов нам нужен специальный набор методов математической статистики.
Казалось бы, статистика существует уже давно, все нужные формулы уже явно придуманы, нужно их просто взять и реализовать. Увы, на деле основная часть классического матстата нам не очень подходит. И сегодня мы будем обсуждать, почему так и что с этим делать.
Нормальное распределение
И начнем мы разговор с нормального распределения. Наверняка вы видели подобную картинку в разных учебниках. Это распределение очень хорошо изучено. Существуют сотни методов, чтобы делать с ним самые разные вещи.
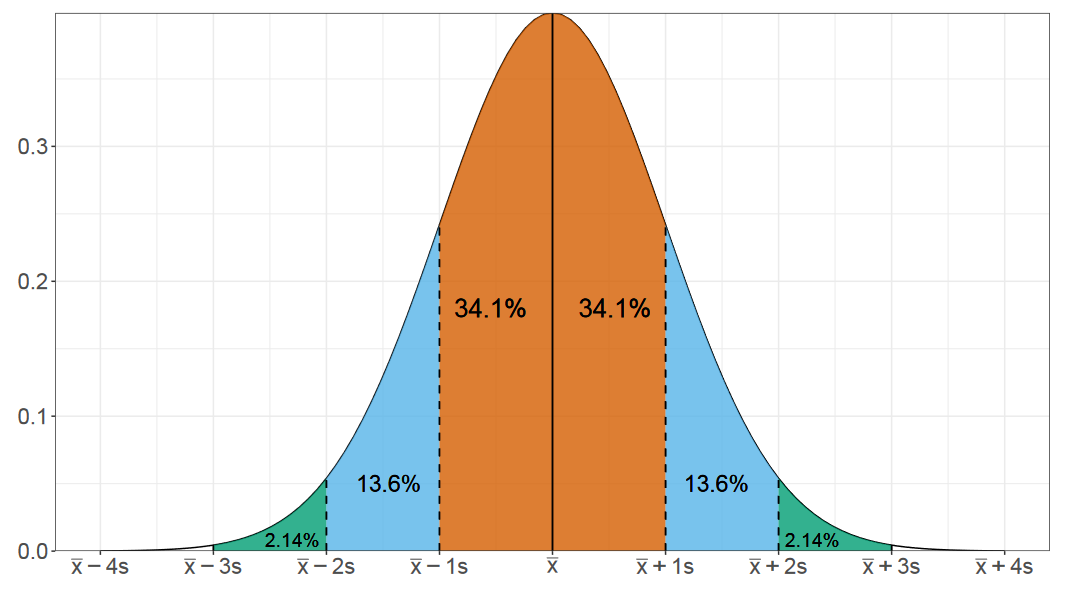
Нормальность — миф: в реальности никогда не было и не будет нормального распределения.
«Testing for normality», R.C. Geary, 1947
Но, увы, в реальности нормальное распределение можно встретить не так уж и часто. Особенно в перформанс-анализе.
Справедливости ради нужно сказать, что в нанобенчмаркинге что-то похожее на нормальное распределение действительно часто возникает. Но как только мы переходим хотя бы к микробенчмаркингу, как только у нас появляются операции или с диском, или с сетью, или хотя бы с оперативной памятью, то перформанс-распределения перестают напоминать нормальную картинку.
Обманчивые средние и дисперсия
Нормальное распределение описывается двумя параметрами: средним значением и стандартным отклонением. Но в случае ненормальных распределений эти параметры для нас не очень полезны, т.к. они не способны описать форму распределения.
На прошлом докладе мы также обсуждали замечательный пример из статьи 2017 года, в которой приводились разные наборы точек, для которых совпадают значения средних значений и дисперсий по x и y, а также коэффициент корреляции между двумя координатами.

Как мы видим, два числа не очень годятся для описания произвольных распределений. Тут нужно понимать, что если нам повезло получить что-то похожее на нормальное распределение, то мы действительно можем обойтись средним и дисперсией. Но такой подход не работает в общем случае.
Давайте посмотрим как выглядят типичные перформанс-распределения из реальной жизни.
Самопальный IO-бенчмарк
Для этого напишем простой самопальный бенчмарк на C#, который работает с диском. Я намеренно не стал использовать специальные библиотеки для бенчмаркинга, чтобы посмотреть на настоящие честные сырые данные.
В нашем бенчмарке мы будем делать 1000 итераций, внутри которых будем создавать файл на 64MB.
int N = 1000; // Количество итераций
var measurements = new long[N];
byte[] data = new byte[64 * 1024 * 1024]; // 64MB
for (int i = 0; i < N; i++)
{
var stopwatch = Stopwatch.StartNew();
var fileName = Path.GetTempFileName();
File.WriteAllBytes(fileName, data);
File.Delete(fileName);
stopwatch.Stop();
measurements[i] = stopwatch.ElapsedMilliseconds;
}Код максимально простой: N раз мы создаем файл на диске, пишем туда 64MB, а затем удаляем этот файл. Каждую итерацию замеряем и сохраняем результаты замеров. Далее мы запускаем этот код на операционной системе Windows и начинаем наслаждаться результатами.
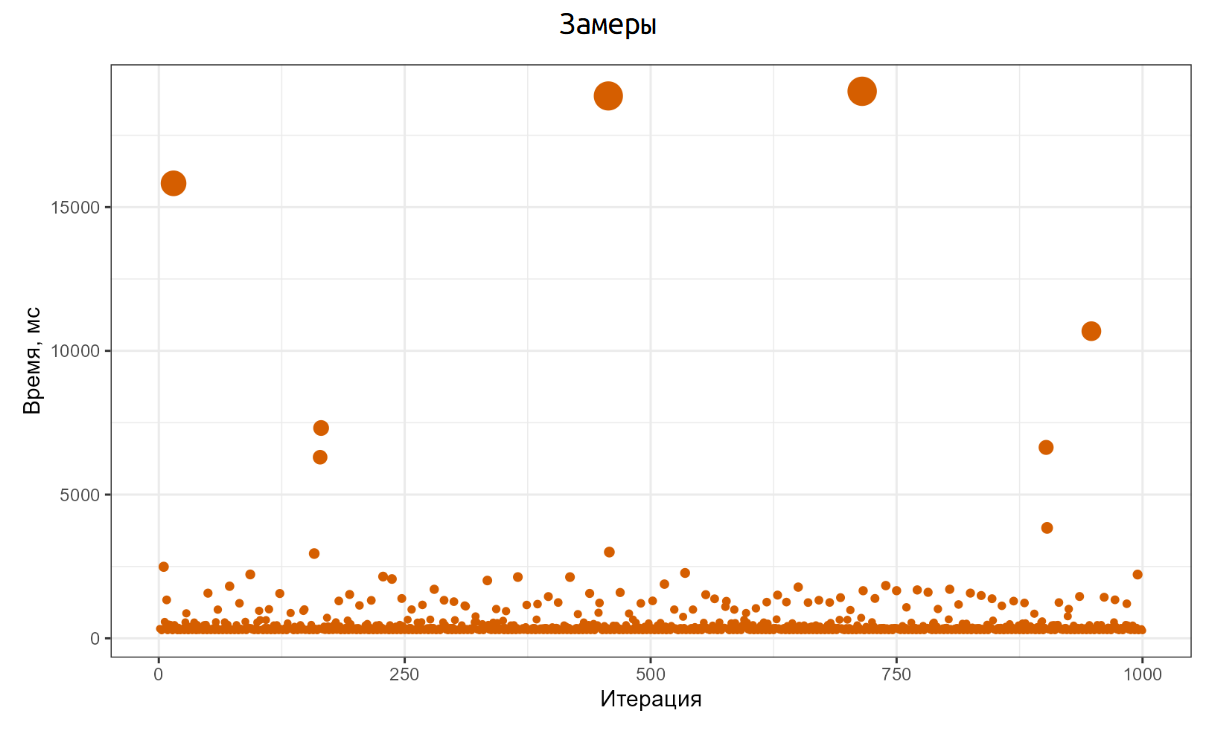
Вот как эти результаты выглядят. Основная часть итераций прошла примерно на 200ms, но есть отдельные итерации, которые заняли 15–16 секунд. И это та реальность, с которой нам нужно научиться работать.
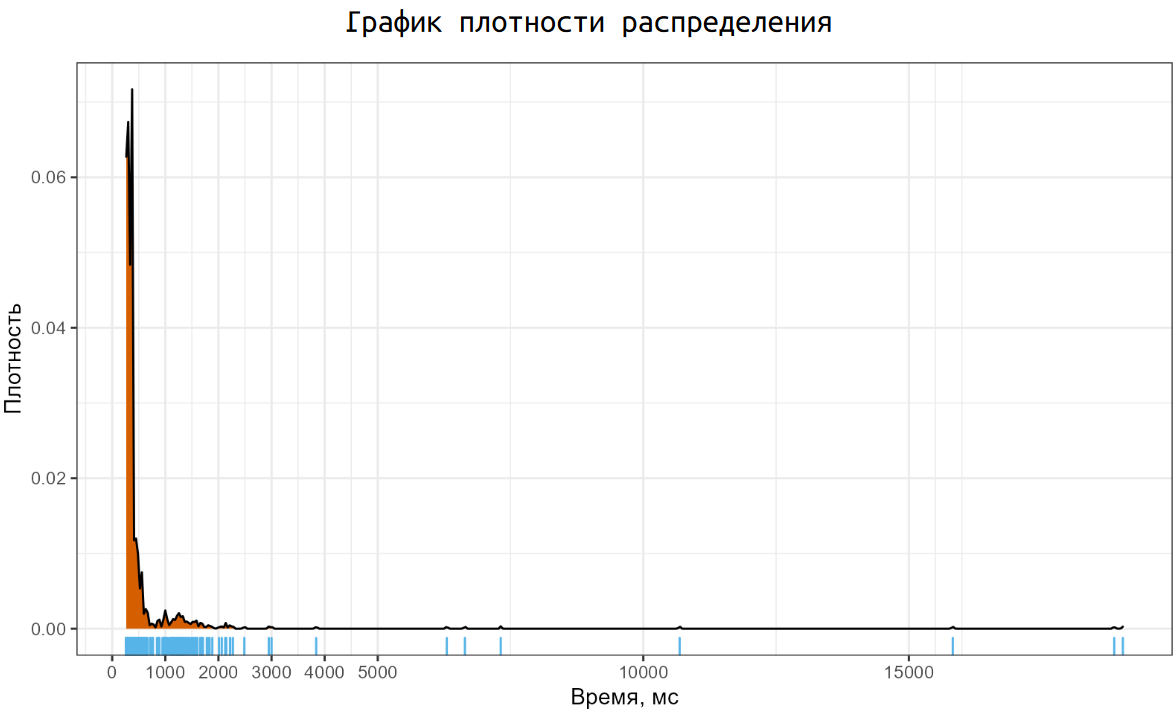
Соответствующий график плотность распределения выглядит не очень приятно. У нас есть одна большая мода около 200ms, маленькая мода между одной и двумя секундами, а также некоторое количество неприлично больших выбросов. И такой график мы получили на одной простой операции по созданию файла. А если рассматривать распределения замеров с реальных систем, то там можно найти намного более страшные картинки.
Основные проблемы
Давайте кратко пробежимся по основным проблемам, которые у нас есть:
Замеры не локализованы в небольшой окрестности, они могут быть размазаны по числовой оси и покрывать большой интервал значений.
У рассматриваемых распределений зачастую тяжелые хвосты, которые дают экстремальные выбросы.
Многие распределения имеют несколько мод.
Иногда проявляются эффекты дискретизации, когда непрерывные распределения начинают потихоньку превращаться в дискретные.
Распределения чаще всего сильно асимметричные, что добавляет некоторое количество проблем.
В этой серии
Итак, о чем же мы будем говорить сегодня? Мы будем обсуждать описательную статистику, а именно: мы будем учиться описывать перформанс-распределения с помощью набора некоторых метрик.
Более конкретно мы обсудим:
центральную тенденцию;
квантильные оценки;
вариацию;
графики плотности распределений;
мультимодальность;
теорию экстремальных значений, которая может помочь в оценке экстремальных квантилей.
Увы, мы не успеем поговорить о сравнении разных распределений и написании стабильных перформанс-тестов, так как этих базовых тем для одного доклада и так уже очень много.
Предупреждение
Данный доклад является чисто математическим. Мы не будем обсуждать программирование, бенчмаркинг, автоматизацию и прочие темы, мы сосредоточимся исключительно на описательной статистике.
Если вы заинтересовались, то давайте вместе отправимся в увлекательный мир математической статистики:
Зачем?
Прежде чем мы начнем, хочу сказать еще пару слов на тему того, зачем все это нужно.
Последние девять лет я мейнтейню библиотеку BecnhmarkDotNet, которая позволяет просто писать надежные .NET-бенчмарки.

На текущий момент библиотека очень популярна: у нас есть тысячи звездочек на GitHub и десятки тысяч пользователей — от маленьких утилит до самого .NET-рантайма.
Как правило, результаты BenchmarkDotNet довольно надежны, но иногда случаются статистические казусы, и результаты могут быть не до конца понятными, что приведет к искаженному представлению об истинном перформансе ваших бенчмарков. Сейчас я работаю над новым статистическим движком, который должен значительно уменьшить вероятность возникновения подобных казусов.
А еще у меня есть проект Perfolizer, в котором я собираю разные математические алгоритмы для надежного перформанс-анализа.

Пока что еще проект все еще на ранних этапах своего развития, но однажды он должен стать основной для создания стабильных перформанс-тестов и систем перформанс-мониторинга.
Однако, даже если у вас есть набор готовых инструментов и методов для анализа, но вы не понимаете устройства перформанс-распределений и связанных с ней проблем, то использовать эти инструменты будет не так уж и просто.
Давайте разбираться что же такого там сложного.
Центральная тенденция
Начнем мы с центральной тенденции. Этот термин выражает естественное желание человека сжать сложное перформанс-распределение до одного единственного числа.
Как же это сделать?
Среднее арифметическое
Самый простой и классический вариант центральной тенденции — это среднее арифметическое. Если у нас есть выборка из n чисел, то мы можем просто сложить все эти числа и поделить сумму на их количества.
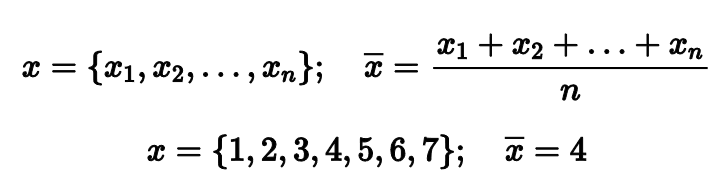
Например, если мы возьмем выборку из первых семи натуральных чисел, то среднее арифметическое будет равно четырем. Довольно ожидаемый хороший результат.
Но стоит в выборке оказаться одному-единственному выбросу, как среднее арифметическое перестает быть надежным показателем центральной тенденции. Если в нашем примере заменить 7 на 273, то среднее станет равняться 42. Согласитесь, это не лучшее описание того, что происходит у нас в распределении.
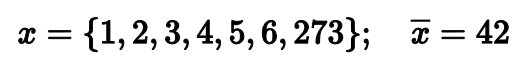
Математики говорят, что среднее арифметическое не является робастным. Это значит, что оно не устойчиво к выбросам. Хватит одного-единственного экстремально большого значения, чтобы полностью испортить результат.
При обсуждении этой проблемы классическое простое решение заключается в использовании медианы. Давайте попробуем!
Среднее арифметическое vs. медиана
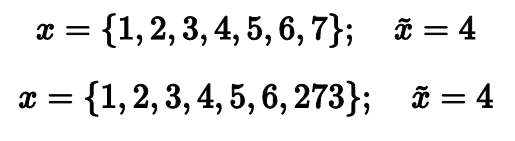
Действительно, медиана обеих выборок равна четырем, что вполне соответствует нашим ожиданиям. Может, на этом стоит и закончить? Давайте всегда использовать медиану вместо среднего арифметического и будет нам счастье!
Увы, такое счастье будет неполным. Замена среднего медианой не проходит бесплатно. Но чтобы понять сопутствующие проблемы, нам нужно обсудить такое понятие, как Гауссова эффективность.
Гауссова эффективность
Рассмотрим следующий эксперимент.
Сгенерируем много выборок из нормального распределения. Для каждой выборки посчитаем среднее арифметическое и медиану, а затем из полученных значений построим новые распределения.

Как вы можете заметить, разброс медианных значений выше, чем разброс значений среднего арифметического.
Чтобы описать разницу между разбросами, математики придумали понятие эффективности.
Для расчета эффективности некоторой оценки T нужно посчитать дисперсию значений среднего арифметического и поделить на дисперсию значений рассматриваемой оценки.
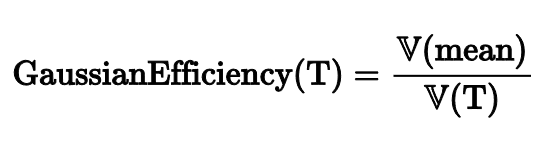
Среднее | Медиана | |
Гауссова эффективность | 100% | 64% |
Для среднего арифметического эффективность равна 100%, так как среднее выступает в роли T. Но если рассмотреть медиану, то ее эффективность равна всего лишь 64%. Это означает, что при замене среднего на медиану результаты наших расчетов начнут сильнее плавать от одного эксперимента к другому.
Это не очень приятно, но такова цена робастности.
Усеченное и винзоризованное среднее
Есть много альтернативных методов расчета центральной тенденции. Другими классическими примерами являются усеченное и винзоризованные средние.
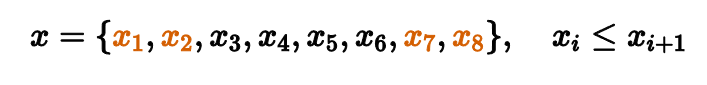
Рассмотрим выборку из восьми отсортированных чисел. Для подсчета медианы нам нужно выкинуть все элементы кроме одного-двух, которые находятся посередине. Таким образом мы повышаем робастность, но понижаем эффективность.
Но что, если мы выкинем только несколько самых маленьких и самых больших значений, а затем посчитаем среднее арифметическое от того, что осталось?
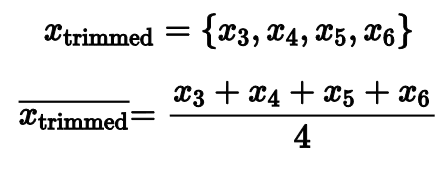
Именно таким образом работает усеченное среднее. Этот способ более робастный, чем обычное среднее, и более эффективный, чем медиана.
Есть еще один альтернативный вариант, который называется винзоризованное среднее. В этом подходе самые маленькие и самые большие элементы не выкидываются, а заменяются на другие элементы.
В нашем примере мы заменяем х₁и х₂ на x₃, а x₇ и x₈ на x₆.

Далее мы считаем обычное среднее арифметическое для того, что осталось.
Оба подхода имеют место быть, они дают предсказуемые значения робастности и эффективности. Но зачастую они оказываются не очень оптимальными. Если мы выкидываем или винзоризируем фиксированное количество элементов, то это количество чаще всего оказывается либо слишком маленьким, либо слишком большим.
Тут может появиться желание сделать более адаптивный подход. Если среднее арифметическое портится от выбросов, то, может, нам просто найти эти выбросы и выбросить их из выборки? Давайте попробуем.
Выбрасываем выбросы
Как же нам найти выбросы?

Если мы погуглим, то по первым ссылкам нам скорее всего предложат использовать границы Тьюки. Это простая формула, которая очерчивает некоторый интервал и объявляет выбросами все элементы выборки вне интервала. На простых академических примерах это работает неплохо, но в реальной жизни нам начнут встречаться проблемы: чаще всего обычные нормальные элементы выборки помечаются как выбросы, что уменьшает Гауссову эффективность подхода. Но если ослабить условия интервала, то мы начнем пропускать важные выбросы, что поломает нам всю робастность.
Если мы поищем альтернативным способы обнаружения выбросов, то обнаружим, что есть сотни разных методов, которые решают эту задачу.
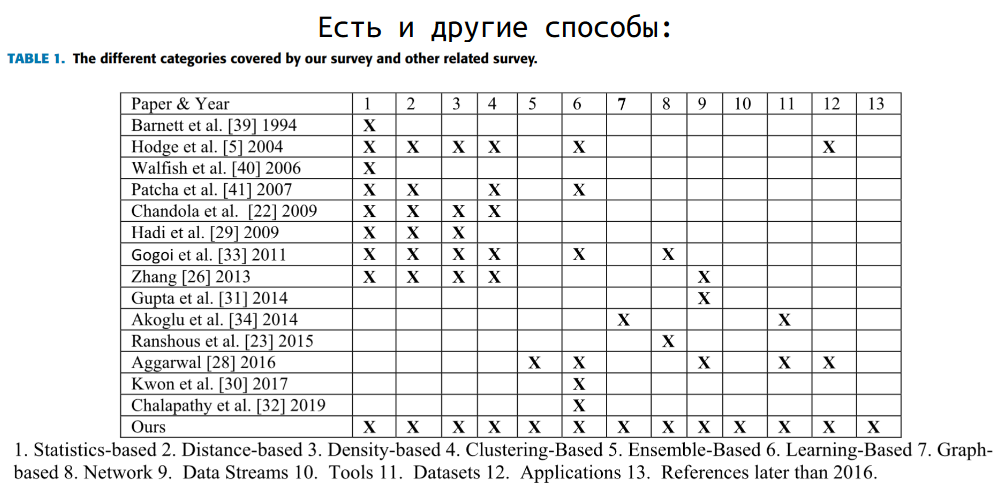
Но мне в целом не очень нравится такой подход.
Во-первых, детекторы выбросов зачастую не очень стабильно работают.
Во-вторых, очень сложно нормально оценить реальные характеристики таких подходов и построить предсказуемую модель анализа.
В-третьих, выбросы являются неотъемлемой частью самого распределения, в которой заключается важная и полезная информация.
Игра в выбрасывание выбросов может легко увести нас в плохую сторону. Я хочу проиллюстрировать важность выбросов одним интересным примером. Он взят из книжки Кэндела 1991 года про изменения климата. И хотя на деле все было не совсем так, он все еще показателен.
Важность выбросов
Об открытии озоновой дыры было объявлено в 1985 году британской командой, работавшей на земле с «обычными» приборами и изучившей свои наблюдения в деталях. Только позже, после повторного изучения данных, переданных прибором TOMS на спутнике NASA Nimbus 7, выяснилось, что дыра формировалась в течение нескольких лет. Почему никто не заметил ее? Причина проста: системы, обрабатывающие данные TOMS, разработанные в соответствии с предсказаниями, полученными из моделей, которые которые, в свою очередь, были созданы на основе того, что считалось «разумным», отвергли очень («чрезмерно») низкие значения, наблюдаемые над Антарктикой во время южной весны. Что касается программы, то, должно быть, в приборе имелся эксплуатационный дефект.
R. Kadnel, Our Changing Climate (1991)
Автор рассказывает историю о том, как 1985 году общественности анонсировали существование дыр в озоновом слое. Однако, данные, которые позволили это сделать, были в наличии уже несколько лет. Почему же эти дыры не обнаружили раньше? Все очень просто. В алгоритме анализа данных ребята решили не учитывать выбросы. Видим слишком низкое значение — убираем его из рассмотрения, чтобы наши средние характеристики не пользовались. Но если выкидывать из рассмотрения аномальные значения, то обнаруживать аномалии резко становится сложнее. Аналогичная ситуация имеет место быть в мире перформанс-замеров.
Скажем, если вы будете игнорировать упавшие по таймауту запросы, чтобы у вас не портилось среднее значение обработки запроса, то вы никогда не найдете проблему, из-за которой эти таймауты возникают.
Какая метрика нам нужна?
Среднее значение — это не всегда то значение, которое нам на самом деле нужно.
Давайте взглянем на распределение Парето. Это то самое распределение, которое описывает ситуации вроде тех, что 20% людей имеют 80% доходов, или что 20% усилий дают 80% результата. Если мы в таком распределении попробуем посчитать среднее арифметическое, то получим довольно большое число, которые язык не поворачивается называть средним.
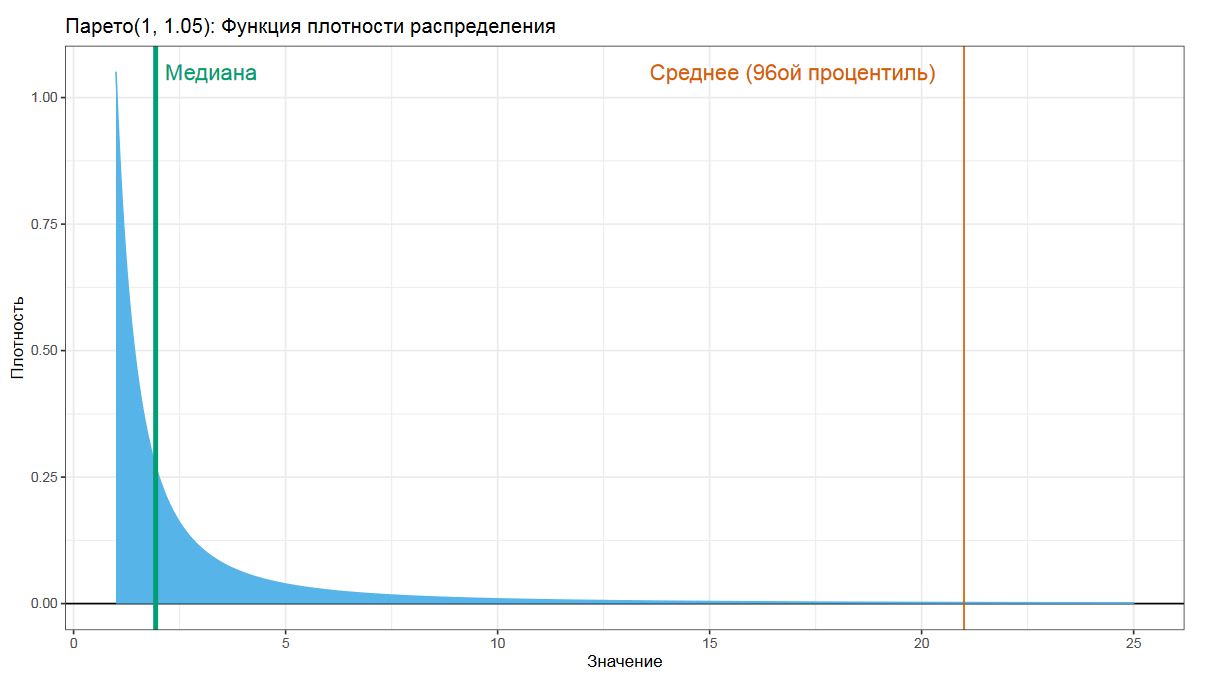
Другое дело — медиана, которая по определению разделяет распределения на две равные части.
При выборе метрики центральной тенденции важно понимать, что мы хотим получить и зачем.
Кроме вариаций средних и медиан есть и другие метрики, которые оценивают центральную тенденцию.
Оценка Ходжеса-Леманна
Я не буду перечислять их все, но мне хочется сказать пару слов про оценку Ходжеса-Леманна, т.к. она обладает интересными свойствами.
Оценка строится очень просто: нужно рассмотреть все пары чисел из нашей выборки, для каждой пары посчитать среднее арифметическое, а затем из полученных средних выбрать медиану.
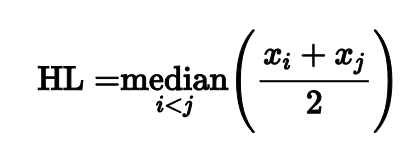
Такой незамысловатый подход дает оценку с интересными свойствами.
Сравнение
Асимптотическая Гауссова эффективность Ходжеса-Леманна 96%. Она почти не уступает среднему арифметическому.
Среднее | Медиана | Ходжес-Леманн | |
Гауссова эффективность | 100% | 64% | 96% |
«Но что там с робастностью?» — спросите вы.
Для оценки робастности есть еще одна полезная метрика под названием точка перелома (на английском breakdown point). Она характеризует процент выборки, который мы можем заменить произвольно большими значениями, чтобы при этом сама оценка не попортилась.
Точка перелома среднего арифметического — 0%, т.к. один единственный элемент может полностью исказить оценку среднего.
Точка перелома медианы — 50%, т.к. мы можем произвольно менять половину чисел в выборке без изменения значения медианы.
А вот для Ходжеса-Леманна точка перелома 29%, что довольно хорошее значение с практической точки зрения.
Среднее | Медиана | Ходжес-Леманн | |
Гауссова эффективность | 100% | 64% | 96% |
Точка перелома | 0% | 50% | 29% |
Действительно, если 29% выборки составляют экстремальные выбросы, то это уже не совсем выбросы, это отдельная группа замеров, которую нужно отдельно изучать и описывать.
При этом 96% — очень хорошая Гауссова эффективность, что делает Ходжеса-Леманна достойной заменой среднему арифметическому как на околонормальных распределениях, так и на распределениях произвольной формы.
Другие метрики
Есть много других интересных метрик для описания центральной тенденции:

И многие другие метрики, для каждой из которых найдутся релевантные сценарии использования.
Вывод
Хотелось бы подчеркнуть основную мысль. Для выбора центральной тенденции нужно хорошо подумать. Подумать о том, зачем вы считаете эту метрику, какие у нее статистические характеристики, на каких распределениях вы будете ее считать.
Только с учетом всех явных и неявных бизнес-требований можно принять разумное решение. Простые подходы вроде «я где-то слышал, что нормальные ребята считают медиану, поэтому давайте мы тоже будем считать медиану» редко дают оптимальный результат.
Мы переходим к нашей следующей теме под названием «квантильные оценки».
Квантильные оценки
Чтобы лучше понять предмет обсуждения, давайте взглянем на график плотности некоторого распределения.
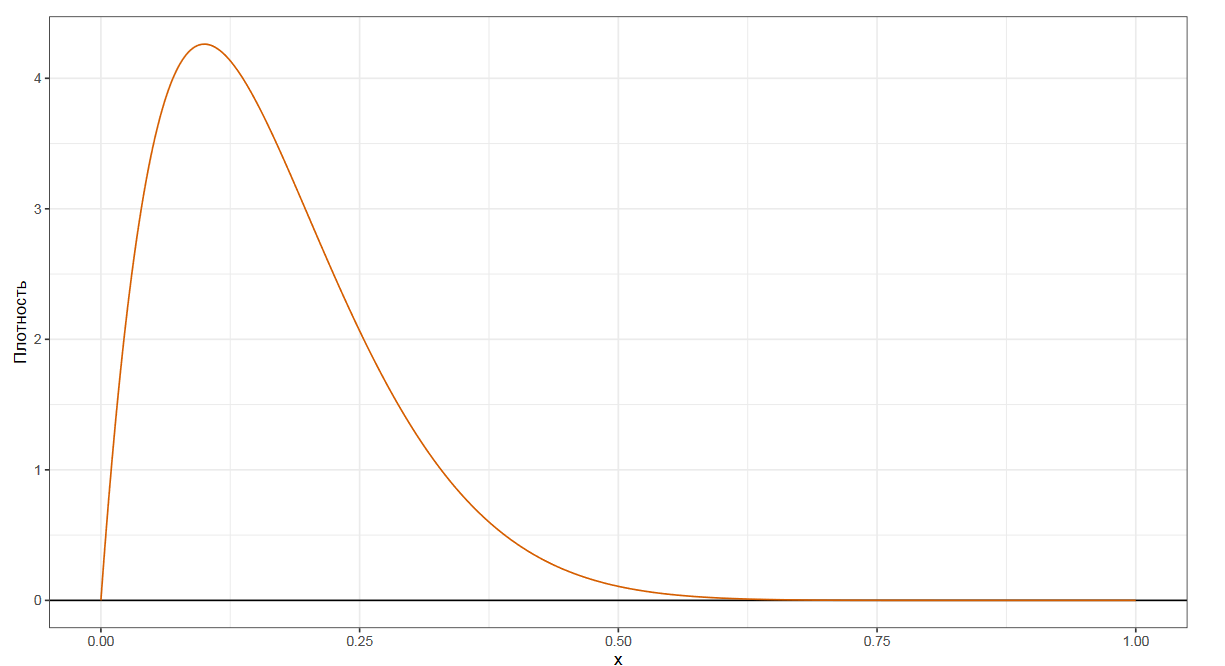
Мы уже знакомы с самой популярной квантильной оценкой — медианой. Она делит наше распределение на две равные части. Если взять случайное число из распределения, то в 50% случаев оно будет ниже медианы, а в других 50% случаев — выше медианы.
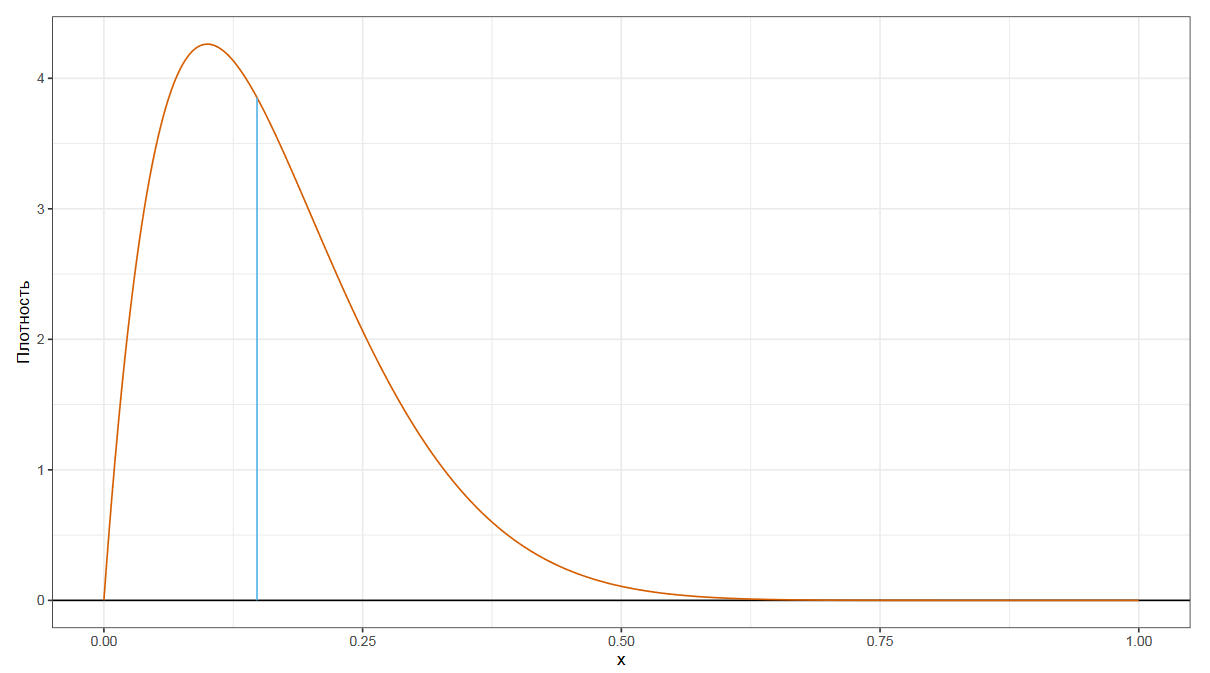
Следующим по популярности видом квантильных оценок являются квартили. Это три числа, которые делят распределение на четыре равные части.
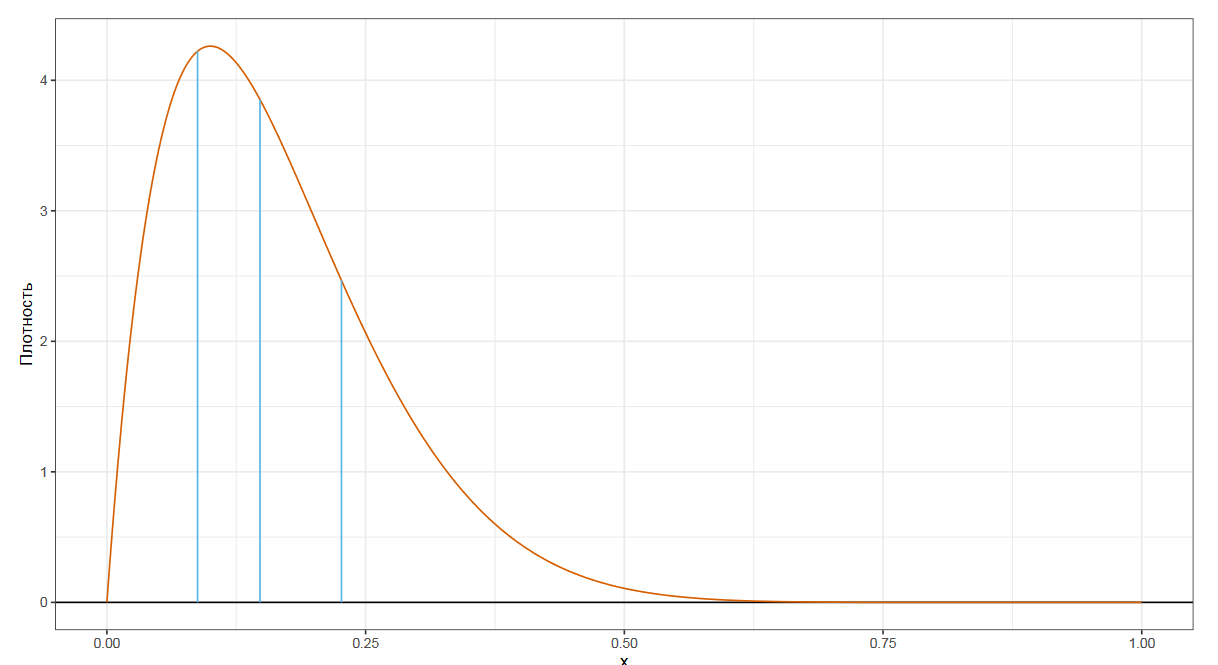
Еще мы можем рассмотреть децили, которые делят распределение на десять равных частей.
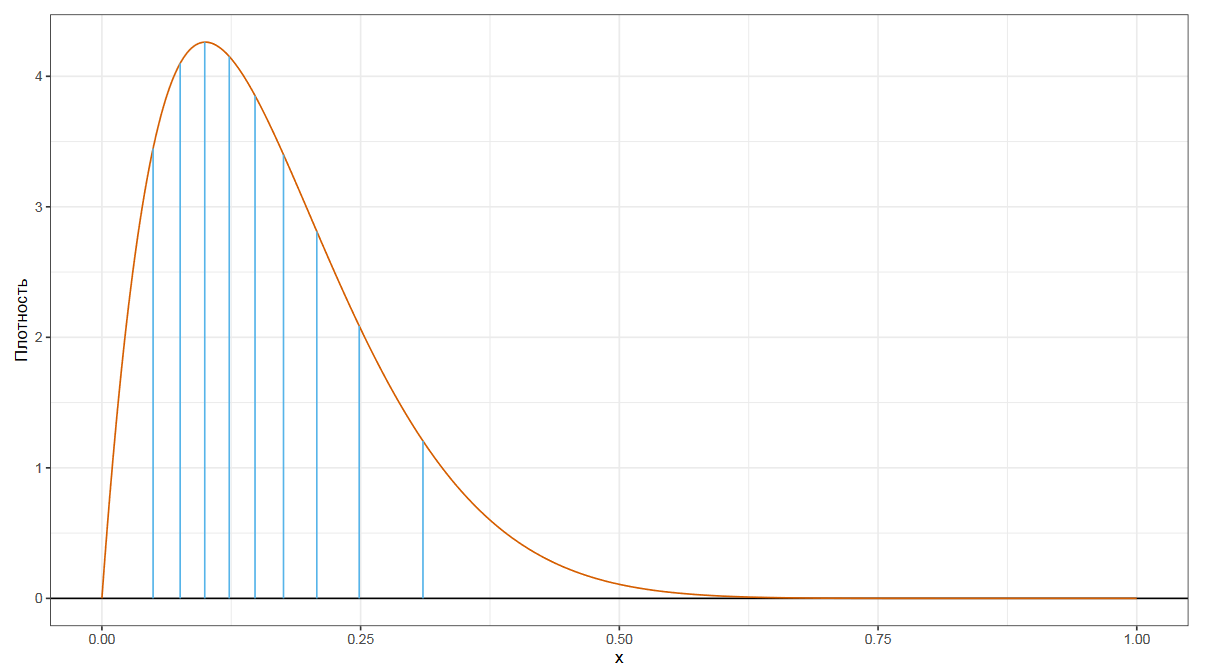
Процентили делят распределение на сто равных частей.
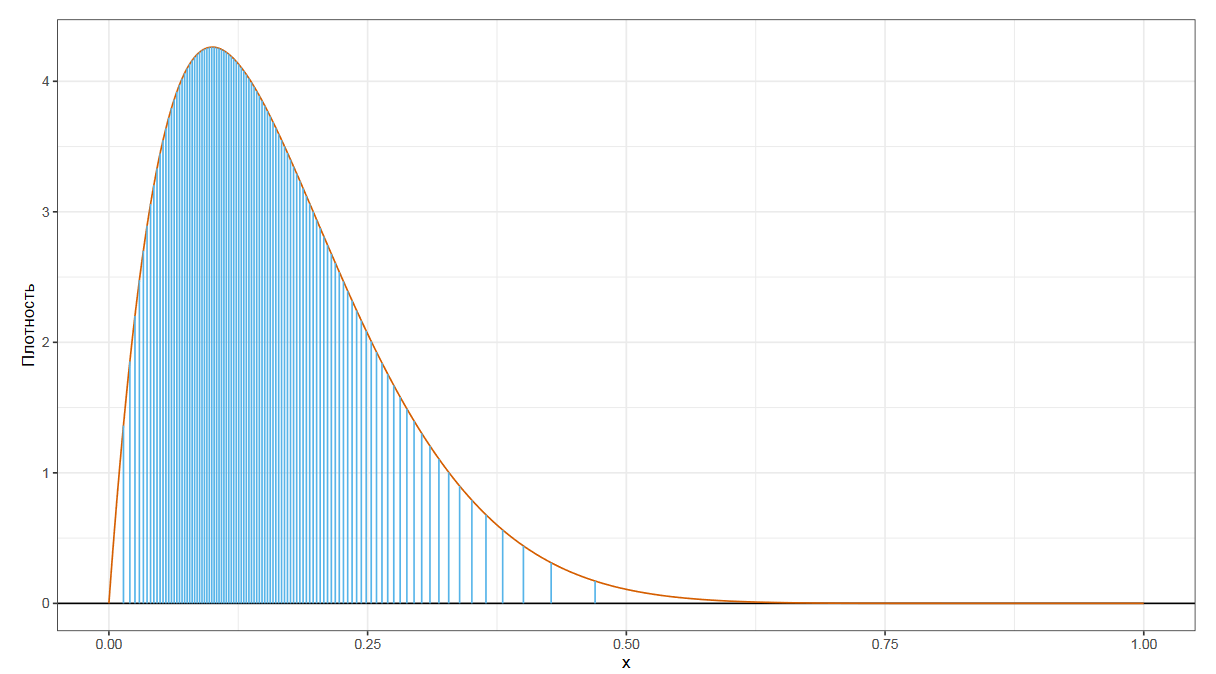
Квантили — это обобщение для вышеобозначенных понятий.
Квантиль порядка p — это такое число, для которого случайное число из данного распределения с вероятностью p оказывается ниже значения p-ого квантиля, и с вероятностью 1-p выше него.
Квантили распределения и квантили выборки
Стоит различать истинные квантили распределения и квантильные оценки, основанные на некоторой выборке. Чтобы лучше понять разницу, давайте рассмотрим небольшую выборку из нормального распределения.

Для данной выборки мы можем посчитать квартили стандартным способом, которому обычно обучают в школе или на первых курсах университета.
К стандартным трем квартилям, которые также являются 25-м, 50-м и 75-м процентилями, часто добавляют так называемые нулевой и сотый процентили, которые соответствуют минимуму и максимуму. Формально так делать нельзя, но такая нотация довольно часто используется на практике.
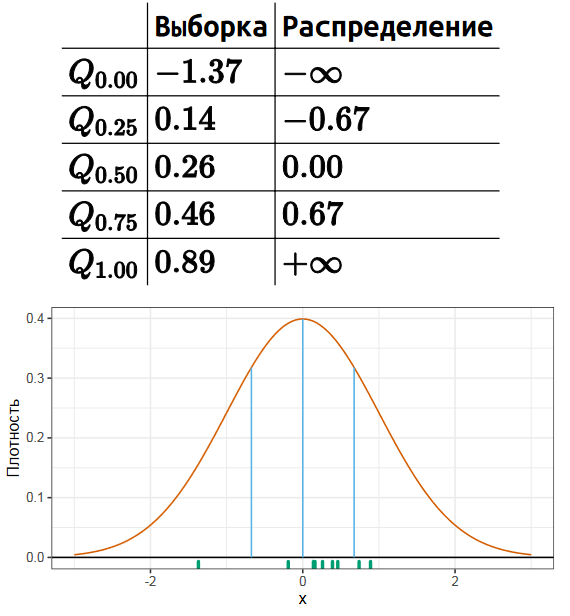
Теперь мы сравним эти числа с истинными значениями соответствующих квартилей распределения. Нетрудно заметить, что они не совпадают. Квантили некоторого распределения всегда фиксированы и являются способом описания этого распределения. А квантили выборки меняются от эксперимента к эксперименту.
Поэтому полное название этих чисел — не квантили, а квантильные оценки. Это попытка оценить истинные квантили распределения по той выборке, которая у нас есть. Но попытка не совсем точная, т.к. конечная случайная выборка не содержит достаточно данных, чтобы точно узнать истинные значения. При этом можно придумать много разных способов угадать истинное значение по данной выборке.
Строго говоря, любая функция из выборки в число может быть рассмотрена как квантильная оценка или оценка любой другой характеристики распределения. Существует некоторое количество стандартных квантильных оценок.
Классификация Хиндмана-Фана
В разных библиотеках можно найти различные варианты квантильных оценок. Если вы попробуете посчитать медиану и прочие квантили с помощью разных библиотек, пакетов, языков программирования или статистических программ, то вы можете получить разные результаты.
В 1996 году Хиндман и Фан сделали обзор формул, которые используются в разных статистических пакетах. Они выделили девять типов классических квантильных оценок.

В настоящее время самым популярным типом является седьмой — он используется по умолчанию в большинстве современных библиотек и статистических пакетов.
Все эти оценки основаны либо на одной порядковой статистике, либо на линейной комбинации двух последовательных порядковых статистик. i-й порядковой статистикой называется i-й элемент выборке после сортировки.
Главные достоинства представленных формул — их простота и быстрота. Если у вас есть отсортированная выборка, то квантильную оценку можно получить за O (1), используя одну тривиальную строчку кода.
Однако данные формулы не всегда дают самый эффективный способ оценки истинных квантилей. Давайте поговорим об альтернативных способах.
Квантильная оценка Харрела-Дэвиса
Мой самый любимый — это квантильная оценка Харрела-Дэвиса. Она рассчитывается как взвешенная сумма всех порядковых статистик.
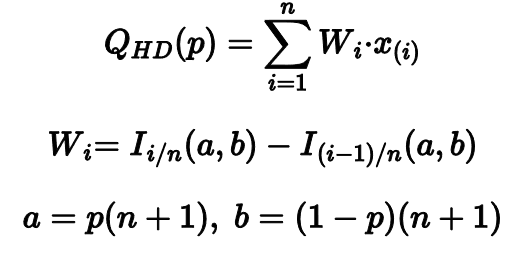
Весовые коэффициенты определяются на основе регулязированной неполной бета-функции. Это может выглядеть сложновато, но основная идея довольная простая.
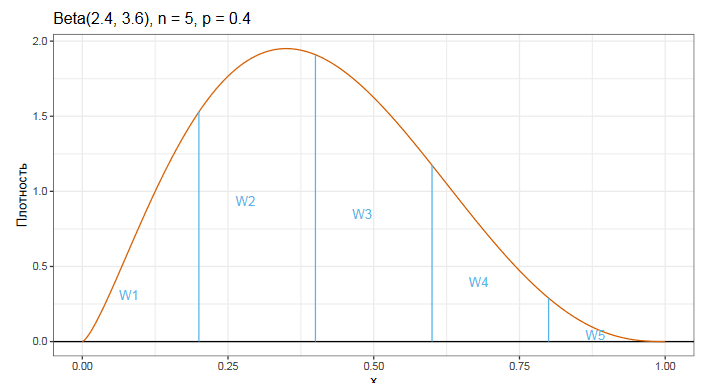
На основе порядка квантиля p и размера выборки n строится бета-распределение. Дальше это распределение делиться на n сегментов, равных по ширине.
Можно использовать следующую интуитивную модель: площадь i-го фрагмента соответствует вероятности того, что p-ый квантиль совпал с i-ой порядковой статистикой.
Таким образом, мы для каждой порядковой статистики определяем вероятность W, с которой эта статистика и является искомым квантилем. Далее строится что-то вроде математического ожидания по всем порядковым статистикам, что и дает нам итоговую квантильную оценку.
Эффективность квантильной оценки Харрела-Дэвиса
Давайте посмотрим на эффективность оценки Харрела-Дэвиса по отношению к классической оценки Хиндмана-Фана седьмого типа.
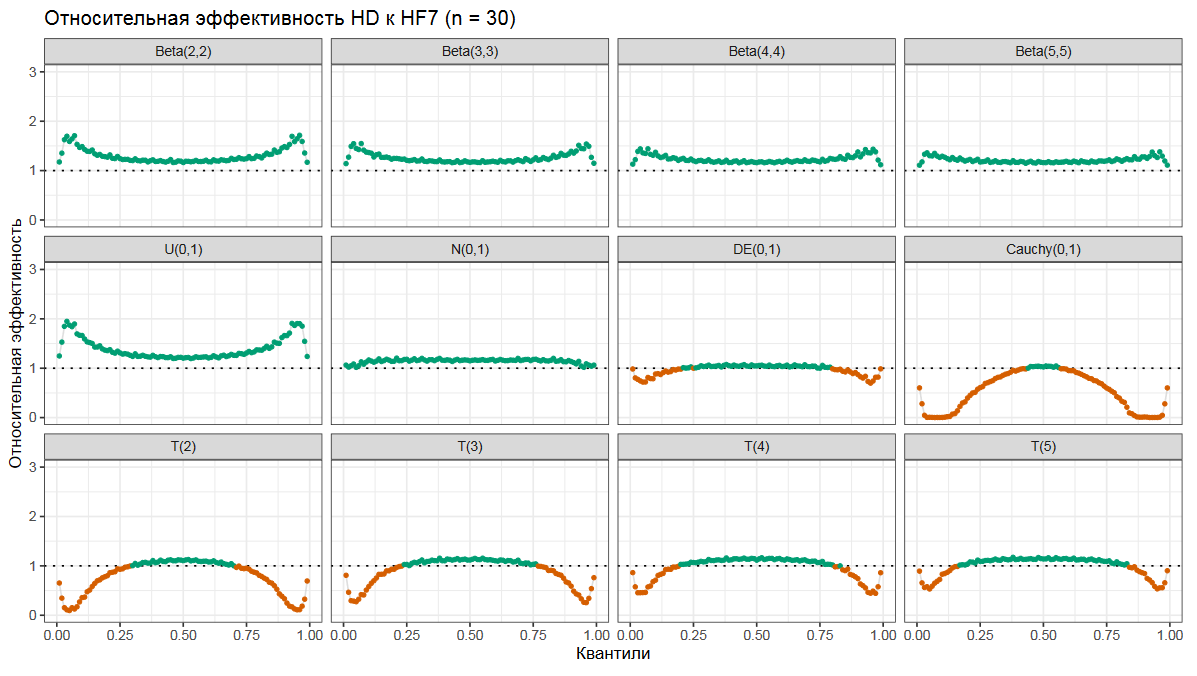
Тут на оси x находятся порядки квантилей, на оси y — относительная эффективность. Когда относительная эффективность больше единицы (что показано зеленым цветом), то это означает, что Харрел-Дэвис победил и оказался более эффективным. Когда относительная эффективность больше единицы (что показано оранжевым цветом), то Харрел-Дэвис проиграл и оказался менее эффективным.
На разных графиках показаны результаты для разных распределений. У нас есть несколько бета-распределений, равномерное распределение, нормальное распределение, двойное экспоненциальное распределение, распределение Коши и несколько Стьюдент-распределений.
Как можно видеть, оценка Харрела-Дэвиса обычно оказывается более эффективной для расчета медианы, но она не всегда эффективна в хвостах распределения.
Доверительные интервалы Мэритц-Джэррэт
Рассмотренный подход с бета-распределением позволяет делать другие интересные вещи. Например, мы можем рассчитывать доверительные интервалы квантильных оценок.
Для этого мы можем рассмотреть моменты квантильных оценок. Для расчета k-ого момента нужно взять весовые коэффициенты W, которые используются для расчета оценки Харрела-Дэвиса, но умножать мы их будем не просто на i-ую порядковую статистику, а на i-ую порядковую статистику в k-ой степени.
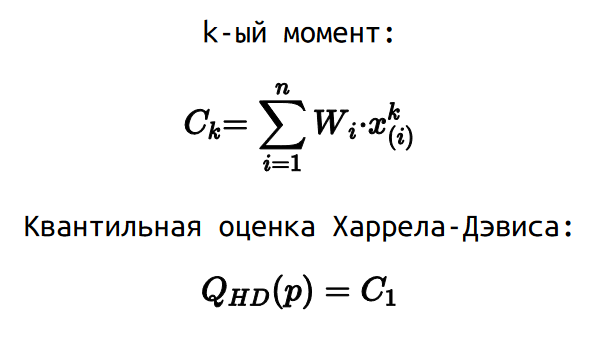
В данной нотации квантильная оценка Харрела-Дэвиса — это просто первый момент. В 1978 году Мэритц и Джэррэт показали, что можно рассчитать стандартную квантильную ошибку как квадратный корень из разницы второго момента и квадрата первого момента.
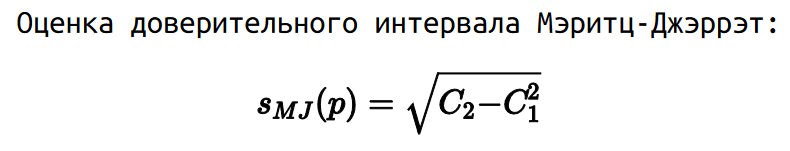
Ну, а на основе стандартной ошибки можно стандартным способом рассчитать доверительный интервал.
Можно делать и другие интересные штуки. Позвольте мне представить авторскую разработку под названием усеченная квантильная оценка Харрела-Дэвиса.
Усеченная квантильная оценка Харрела-Дэвиса
У классической оценки Харрела-Дэвиса есть один недостаток: она не робастная. Так как она использует взвешенную сумму всех элементов выборке, то одно экстремальное значение может испортить все квантильные оценки. Это неприятная цена, которую приходится платить за повышенную статистическую эффективность.
Давайте внимательно посмотрим на бета-распределение, которое определяет весовые коэффициенты порядковых статистик для медианы по Харрелу-Дэвису.

У центральных порядковых статистик веса довольно большие, а у хвостовых порядковых статистик — маленькие. Если мы немножко подумаем, то поймем, что хвостовые порядковые статистики практически не влияют на эффективность, но при этом практически полностью уничтожают робастность.
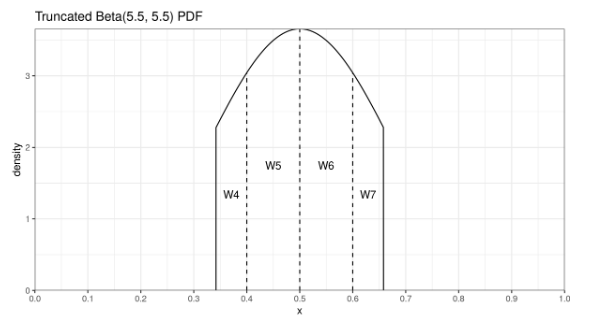
При расчете усеченного варианта оценки мы отбрасываем элементы с малыми весовыми коэффициентами и используем только порядковые статистики с большими весами. В итоге мы совсем чуть-чуть теряем в эффективности, но зато заметно улучшаем робастность. А еще этот способ быстрее с вычислительной точки зрения, т.к. нам нужно вычислять меньше значений регулязированной неполной бета-функции.
Такой подход очень хорошо зарекомендовал себя на практике. Когда мне нужно эффективно вычислить медиану, то чаще всего я беру именно усеченную оценку Харрела-Дэвиса.
Квантильная оценка Сфакианакиса-Виргиниса
Есть и другие способы расчета квантильных оценок. Как мы видели, оценка Харрела-Дэвиса часто бывает не очень эффективна для хвостовых квантильных оценок. В 2008 году Сфакианакис и Виргинс попробовали побороть эту проблему. Они предложили три новых варианта квантильных оценок.

Общая идея похожа на подход Харрела-Дэвиса, но вместо бета-распределения используется биномиальное распределение. Плюс есть специальная коррекция, призванная увеличить эффективность оценок в хвостах.
Квантильная оценка Навруза-Оздемира
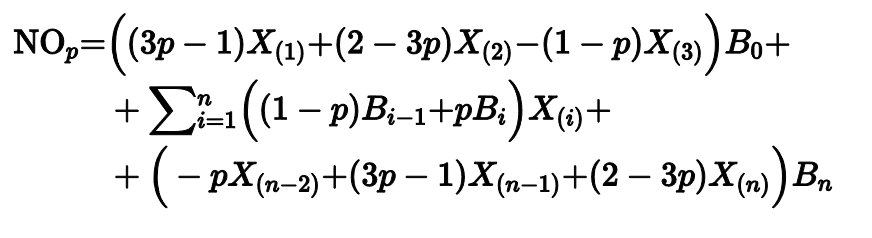
Другим вариантом этого подхода является оценка Навруза-Оздемира, предложенная в 2020 году.
Подробнее о ней можно прочитать здесь.
Проблема: агрегация истории коммитов
С квантильными оценками можно много играться, приспосабливая их к различным задачам. Давайте рассмотрим проблему агрегации истории коммитов.
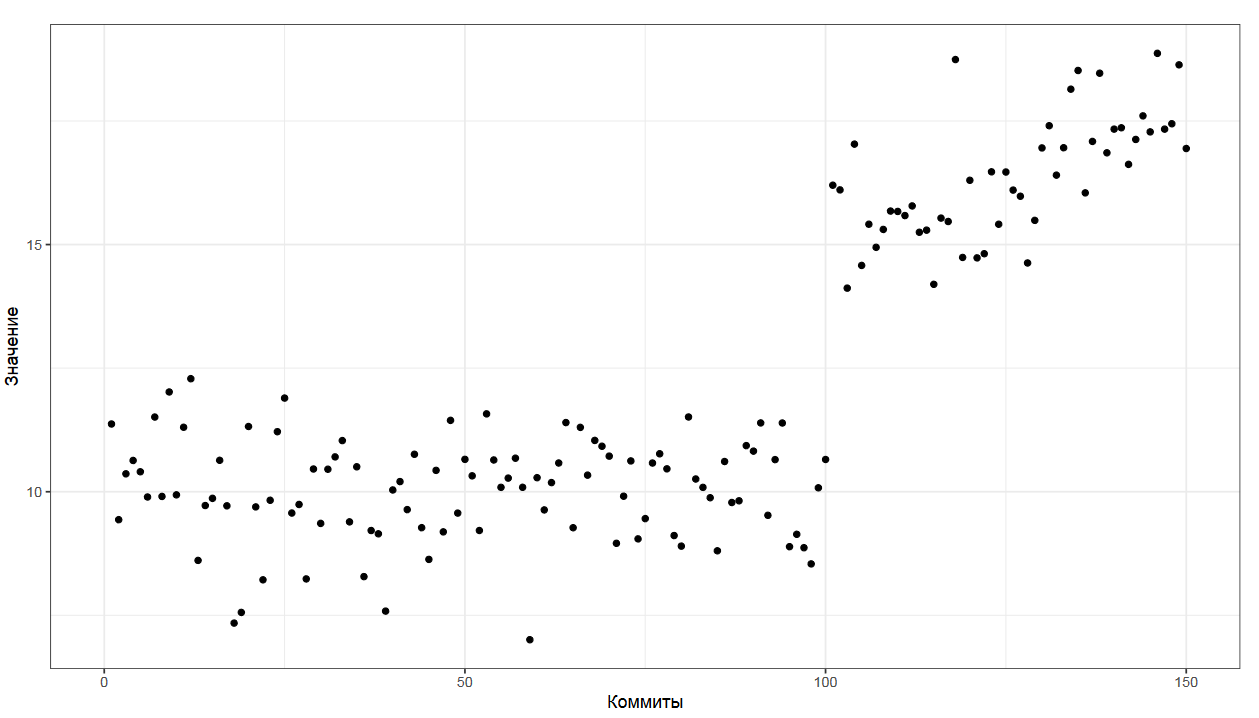
Представьте, что у вас есть некоторый метод, перформанс которого вы замеряете один раз на каждый коммит. Вам хочется получить описание распределения, которое у вас есть прямо сейчас для последнего коммита в истории. Но для этого коммита у вас есть только один замер, которого явно недостаточно, чтобы построить распределение.
Можно взять последние n коммитов, но это чревато проблемами, ведь программисты постоянно меняют код, что влияет на производительность метода непредсказуемым образом. Старые коммиты из истории могут не отражать реального состояния дел.
Чем больше коммитов мы берем, тем больше вероятность попасть на неактуальные замеры.
Чем меньше коммитов мы берем, тем меньше данных у нас есть для построения распределения.
Как же быть?
Взвешенные выборки
Одним из подходов являются взвешенные выборки, на основе которых мы можем реализовать экспоненциальное сглаживание.
Давайте рассмотрим некоторую выборку. Каждому элементу выборки мы сопоставляем некоторый вес. В нашем примере мы можем использовать экспоненциальный закон для расстановки весов.

К примеру, самый последний коммит имеет вес 1, предпоследний коммит имеет вес 0.5, предпредпоследний элемент имеет вес 0.25 и так далее.
Экспоненциальную функцию весов можно растягивать. К примеру, вес 0.5 может быть у коммита недельной давности или месячной давности, при этом прочие веса корректируются соответствующим образом. Имея подобные весовые коэффициенты, можно реализовать экспоненциальное сглаживание.
Для среднего арифметического подобное сглаживание делается очень легко и записывается простой формулой.
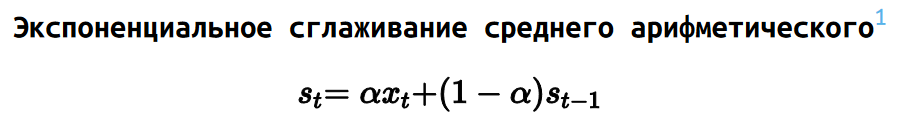
Из-за того, что среднее арифметическое не является робастным, выбросы заставляют прыгать значение среднего туда-сюда, что не совсем удобно для задач мониторинга. Но, как мы знаем, среднее арифметическое — это не всегда та метрика, которую мы хотим знать. К счастью, экспоненциальное сглаживание можно применить и к квантильным оценкам.
Например, можно построить взвешенную версию оценки Харрела-Дэвиса, изменяя площадь сегментов рассматриваемой бета-функции.
