Очень сложные Крестики-Нолики или Монтеки-Карлоки24.11.2023 20:00

Доброго времени суток, когда вы в последний раз играли в крестики-нолики? Вопрос действительно важный, не удивляйтесь, всё окажется гораздо хитрее чем вы думали. Полагаю что давно, хорошо, вспомните поле которое вы рисовали на бумаге: 3×3? 5×5? А что вы скажете насчёт 19×19?»Долго будем играть!» — и это только часть проблемы. Если вы крайне дотошный игрок в крестики-нолики и не можете позволить себе проиграть младшему брату в такую игру, то вы конечно попытаетесь анализировать положение поля, пред рассчитать шаги брата и выбрать наилучший. Ход мыслей отличный, однако это вполне несложно на маленьких полях, а вот 19 на 19… Именно такая задача встала передо мной в ходе хакатона от компании Тинькофф — написать бота для игры в крестики-нолики на доске 19×19 с поиском самого лучшего хода за небольшое время.

Как играть в крестики-нолики?

Давай-те теперь сменим обстановку и скажем, что вы чтобы точно обыграть младшего брата написала бота который играет за вас и ищет самые лучшие шаги в некой ситуации. Как мы представим в программе эту самую игру, её правила и доску?

Первая идея — представим доску в виде набора символов и будем смотреть где стоит крестить, а где нолик. Просто? Вполне! Представим себе поле 3×3 где каждый игрок поставил по одной фигуре:

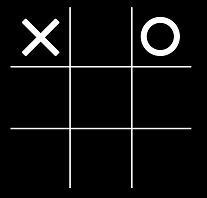
string board_state = "x_o______";

Выглядит неплохо, однако как проверить что кто-то выиграл? Например, можно сравнить наш board_state с примерами выигрышных строк:

string board_state = "x_o______";
string win_patterns[0] = "xxx______";
if(board_state.Equals(win_patterns[0])) 
  Console.Write("Крестики победили!");

Однако, неудобно очевидно то, что таких выигрышных ситуаций будет многовато: в ряд, в столбец, в диагональ слева направо и справа налево — и каждую из таких строк придётся хранить, да и сравнение строк операция не очень приятная. Рассмотрим интересный способ упростить такую программу.

Битовые доски

Подход заключается в том, чтобы представить доску игроков в виде двухзначного числа, где каждый разряд бита — стоит ли фигура на данной позиции или нет. Повторим положение доски с картинки в данном представлении:

uint x_board = 0b100_000_000; // X стоит на 9-ой клетке (считая с правого угла), т.е. в 9 разряде числа
uint o_board = 0b001_000_000; // О стоит на 7-ой клетке, т.е. в 7 разряде числа

Таким образом, вместо строк мы храним одно число, но представляя его в двоичной форме получаем информацию где стоит фигура игрока. Как узнать полное положение доски? Не хитро:

uint full_board = x_board | o_board; // Просто битово умножаем два числа!

Элегантно? Это ещё не всё! Для проверки того, выиграл ли кто-то мы также будем сравнить положения доски с выигрышной ситуацией, но делать мы это будем с помощью операции побитового умножения:

uint x_board = 0b100_000_000; 
uint o_board = 0b001_000_000; 
uint[] win_patterns = 
{   
  0b111_000_000, // 3 в ряд на позициях 9, 8 и 7
  0b000_111_000, // 3 в ряд на позициях 6, 5, 4
  0b100_010_001, // 3 в диагональ слева-направо
  // и так далее
};

if (win_patterns.Any(w => (x_board & w) == w)) Console.Write("X победили!");
else if(win_patterns.Any(w => (x_board & w) == w)) Console.Write("O победили!");

Согласитесь — операция побитового умножения гораздо приятнее (быстрее) сравнения строк.

Масштабируем проблему

И тут многие догадались, как же я хочу решить проблему написания бота для игры в крестики-нолики на поле 19×19. Однако, как мы представим такую доску?

ulong x_board = 0b0000000000000000000_0000000000000000000_... // 19 рядов по 19 ноликов

Такое число превышает 64 бита, что уже больше ulong! А ведь нам ещё хранить победные ситуации! Как будем выбираться? Можно подключить какую-нибудь библиотеку для больших типов данных, но хранить такие переменные? Да и для внешнего восприятия выглядит действительно ужасно. Тогда стоит подумать, доска состоит из строк, почему бы и нам это огромное число разделить не разделить на строки и хранить состояние доски в виде девятнадцати 19-разрядных битовых чисел — строк (рядов) доски?

uint[] x_board = new uint[19]
{
  0b1000000000000000000,
  0b0110000000000000000,
  0b0000000000000000000,
  0b0000000000000000000,
  ... // 19 чисел
}

Тогда спокойно можно использовать uint. Отлично, а как проверять такую красоту на выигрыш (при условии что победа — 5 фигур в ряд, в столбец и диагональ) ? Давайте разбираться, для начала представим все случаи победы в ряд для i-ой строки доски:

private static readonly uint[] _win_patterns_rows =
{
  0b1111100000000000000,
  0b0111110000000000000,
  0b0011111000000000000,
  0b0001111100000000000,
  0b0000111110000000000,
  0b0000011111000000000,
  0b0000001111100000000,
  ... 
};

Тогда чтобы проверить выиграл ли какой-либо игрок будем побитового перемножать i-ую строку из доски игрока на j-ую строку из всевозможных выигрышных строк:

private bool check_if_board_win_pattern_horizontal(uint[] board)
{
  uint horizontal_check;
  uint win_pattern;

  // проходим по каждой строке состояния доски игрока
  for (byte j = 0; j < 19; j++)
  {
    // проверяем каждый выигрышный случай данной строки
    for(byte i = 0; i < 15; i++)
    {
      // проверяем все возможные состояние доски при победе в ряд
      horizontal_check = board[j] & _win_patterns_rows[i];
      win_pattern = _win_patterns_rows[i];
      if (horizontal_check == win_pattern) return true;
    }
  }
  return false;
}

Но это только в ряд, как же в столбец? Представим, что наше двоичное представление доски 19×19 — это бинарная матрица, ведь правда похоже! Тогда нам достаточно просто транспонировать эту матрицу и запустить функцию проверки сверху — ведь столбцы станут строками!

Хорошо, тут разобрались, а как же проверка по диагонали? Попытаемся представить выигрышную позицию в случае победы в диагональ слева-направо:

    private static readonly uint[] _win_patterns_diagnal =
    {
        0b1000000000000000000,
        0b0100000000000000000,
        0b0010000000000000000,
        0b0001000000000000000,
        0b0000100000000000000,
        // остальные строки такой доски будут нулевыми поэтому нет смысла их заполнять
        // нам важны 5 в диагональ
    };

Проверить конкретно такую выигрышную ситуацию мы сможем — перемножим доску какого-либо игрока на эти значения как мы делали выше. Однако нам нужно проверить все случаи 5 фигур подряд в диагональ. Сделаем очень хитрую вещь — представим опять, что наше поле игрока — это матрица 19×19, разделим эту матрицу на все возможные подматрицы 5×19 (так как нам необходимы только 5 столбцов для проверки) и будем умножать их на наш _win_patterns_diagnal, однако затем заново пойдём делать тоже самое применим к каждой строке _win_patterns_diagnal сдвиг вправо на i количество битов. Звучит сложно, посмотрим в виде кода:

private bool check_if_board_win_pattern_diagnall(uint[] board, bool left_to_right)
{
  uint[] _win_patterns;
  uint[] diagnal_check = new uint[5];
  
  for(byte h = 0; h < 19; h++)
  {
    // Сдвигаем матрицу победы наискок чтобы посмотреть все варианты a.k.a
    // 1, 0, 0, 0, 0         0, 1, 0, 0, 0
    // 0, 1, 0, 0, 0   =>    0, 0, 1, 0, 0
    // 0, 0, 1, 0, 0         0, 0, 0, 1, 0
    // ....                     ....
    _win_patterns = (uint[])_win_patterns_diagnal.Clone();

    // Реверсировать каждую строку (число) доски игрока
    // код затычка - нужно будет дописать...
    if (left_to_right) _win_patterns.Reverse();

    _win_patterns[0] >>= h;
    _win_patterns[1] >>= h;
    _win_patterns[2] >>= h;
    _win_patterns[3] >>= h;
    _win_patterns[4] >>= h;
    // Заполняем проверочную матрицу 5x19 (т.к. 5 наискосок)
    for (byte i = 0; i < 5; i++)
    {
      // Проходимся шагом 5, иначе говоря рассматриваем все подматрицы 5x19 матрицы 19x19
     for (byte count = 0; count < 14; count += 5)
      {
        // проверяем все возможные состояние доски при победе в ряд
        diagnal_check = new uint[5];
        diagnal_check[i] = board[count] & _win_patterns[i];
      }
      if (new HashSet(diagnal_check).SetEquals(_win_patterns)) return true;
    }
  }

  return false;
}

Для проверки победы на диагональ справа-налево будем просто реверсировать каждую строку (в коде сверху это не реализовано).

А как же сам алгоритм поиска решений?

Наша команда выбрала два алгоритма для поиска наилучшего хода в такой задаче — Минимакс и Монте-Карло. Мне достался алгоритм Монте-Карло -, но о нём я постараюсь вам рассказать в следующей статье, в контексте данной проблемы.

Для чего это написано?

Во время решения данной проблемы я не нашёл стоящей информации про игры на доске 19×19, их представление в виде битовых досок и ещё очень много чего. Алгоритмы которые я описал были додуманы мною на основе чужих наработок решения той же проблемы на небольших полях (3×3 и 5×5), в частности работа с доской как с набором строк (рядов) и вытекающие отсюда последствия.

Заметки

Так как данная проблема, решалась мной на хакатоне, то время было крайней ограничено — отсюда вытекает то, что описанной мной здесь код может содержать ошибки, буду признателен тем, кто их отыщет!

Также думаю стоит упомянуть, что как и в проверке на 5 в диагональ — так и в проверках в ряд и в столбец можно оптимизировать алгоритм путём динамического битового сдвига.