Обнаружение аномальных звуков сердцебиения на основе записей сердечного ритма

 Автор статьи: Виктория Ляликова
Автор статьи: Виктория ЛяликоваВсем привет! Сегодня рассмотрим задачу обнаружения аномалий тонов сердца, используя аудиозаписи звуков сердцебиения. Для этого будем использовать библиотеку librosa по работе с аудиофайлами, а также классические алгоритмы машинного обучения и методы глубокого обучения.
Возьмем датасет «Heartbeat Sound», который содержит аудиофрагменты сердечных ритмов различной продолжительности от 1 до 30 секунд, как здоровых пациентов, так и имеющих аномальные звуки сердцебиения. Набор содержит 813 аудиофайл с записями, разбитыми по категориям: artefact, extrastole, murmur, normal и unlabel. Попробуем разобраться, что обозначают эти категории.
Normal — как и следует из названия, нормальное сильное ритмичное сердцебиение.
Murmur — записи звука сердца, где присутствуем какой-то шум, например, свист, рев, урчание. Наличие такого шума может быть симптомом многих заболеваний сердца.
Etrastole — экстрасистолические (дополнительные) записи звука, которые могут появляться время от времени и могут быть идентифицированы по отсутствию сердечного тона, включающему дополнительные или пропущенные сердечные сокращения. Экстрасистола может не быть признаком заболевания, но в некоторых ситуациях могут быть вызваны заболеваниями сердца.
Artefact — по сути не является сердцебиением, и характеризуется широким спектром различных звуков. В этой категории содержится широкий спектр различных звуков, включая визги, эхо, речь, музыку. Обычно различимые тоны сердца отсутствуют, важно определять эту категорию записей, чтобы можно было повторить исследование.
Теперь кратко ознакомившись с категориями заболеваний, которые имеет наш датасет, можно переходить к анализу, чтобы лучше понять с какой информацией мы будем работать.
Анализ данных
Загрузим папку с нашими данными и посмотрим на графики сердечного ритма для аудиофайла без аномалий и с аномалиями. Приведен пример кода для построения графика сердечного ритма для normal.
import os
import matplotlib.pyplot as plt
import librosa.display as ld
data_path ='D:/Heartbeat_sound'
os.listdir(data_path)
['artifact','extrastole', 'murmur', 'normal', 'unlabel']
import matplotlib.pyplot as plt
import librosa.display as ld
sr=22050
signal ='*/normal/normal__103_1305031931979_B.wav'
normal, sr = librosa.load(signal, sr = 22050)
librosa.display.waveshow(normal, sr=sr, label='Normal')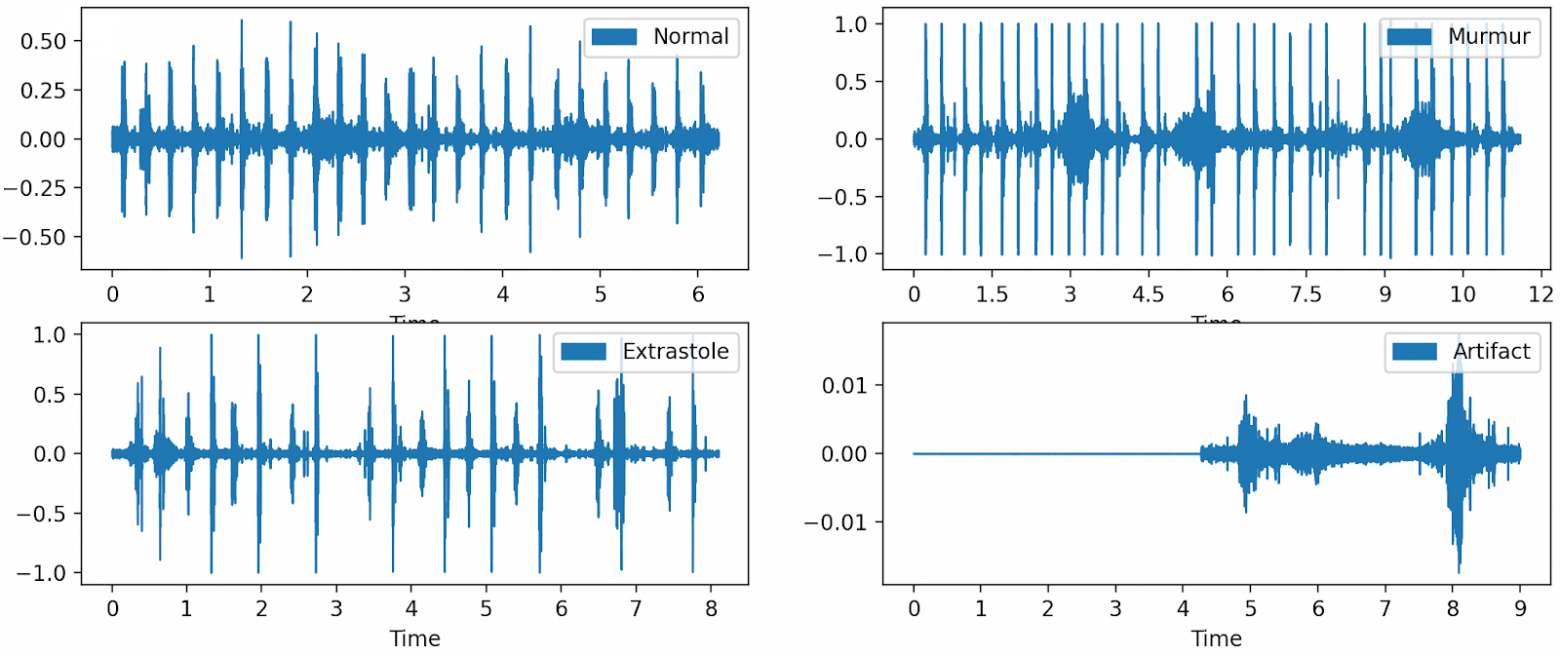
Что здесь можно увидеть? Первый график, то есть график нормального сердцебиения, показывает равномерное распределение амплитуд и постоянство между ударами и ударами звуковой волны. Если сравнить график шумов в сердце с нормальным , то можно заметить, что он кажется менее последовательным и содержит много дополнительных звуковых волн, проходящих между ударами сердца. Экстрасистолические звуки имеют более высокую амплитуду по сравнению с нормальным сердцебиением, и существует большая неравномерность между различными звуковыми волнами, что указывает на то, что может наблюдаться пропуск сердцебиения. График артефактов (artefact) просто показывает зашумленные данные, с которыми можно столкнуться при неправильной попытке сделать запись.
Теперь попробуем объединить все эти графики с записями сердечных ритмов в один рисунок.
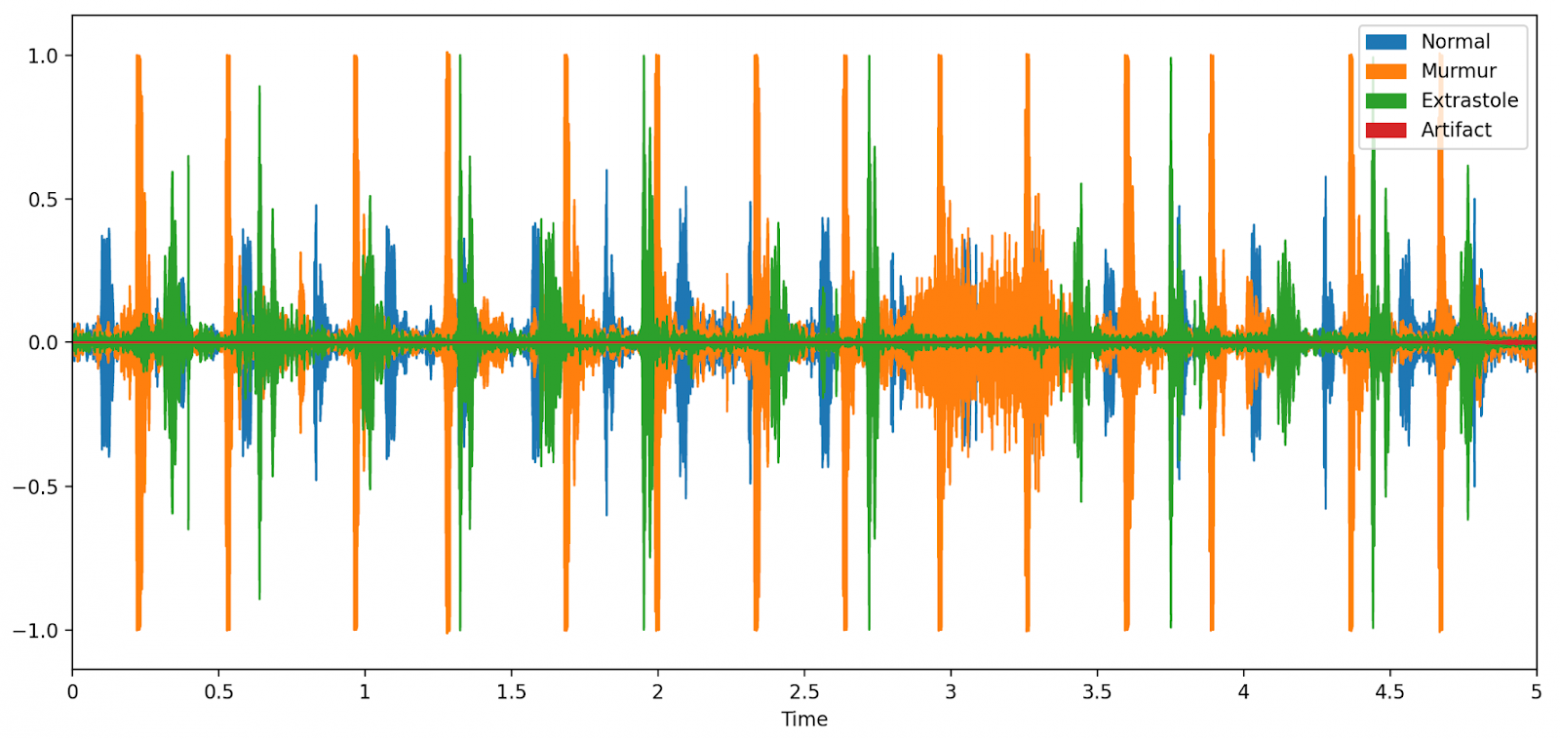
Видно, что экстрасистолические звуки сердцебиения имеют большую амплитуду по сравнению с нормальными тонами сердца, и все различные классификации сердцебиений имеют нерегулярный ритм.
Далее посмотрим на распределение классов, посчитав количество записей в каждой папке и посмотрим на результат, используя диаграмму.
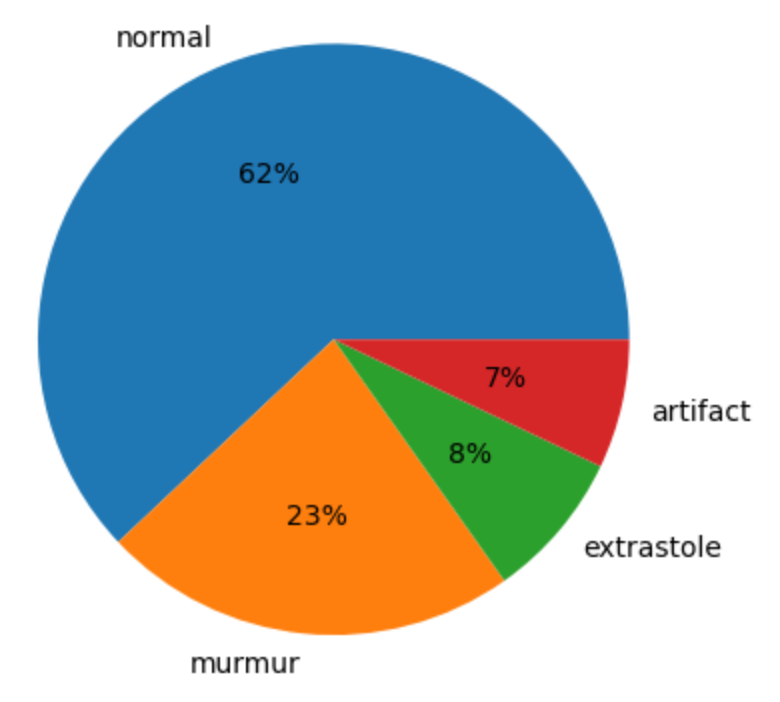
Видим, что данные очень несбалансированы, попробуем позже учесть этот факт при построении моделей. Теперь посмотрим на длительности каждой записи и как это распределяется по количеству записей. Посмотрим на график
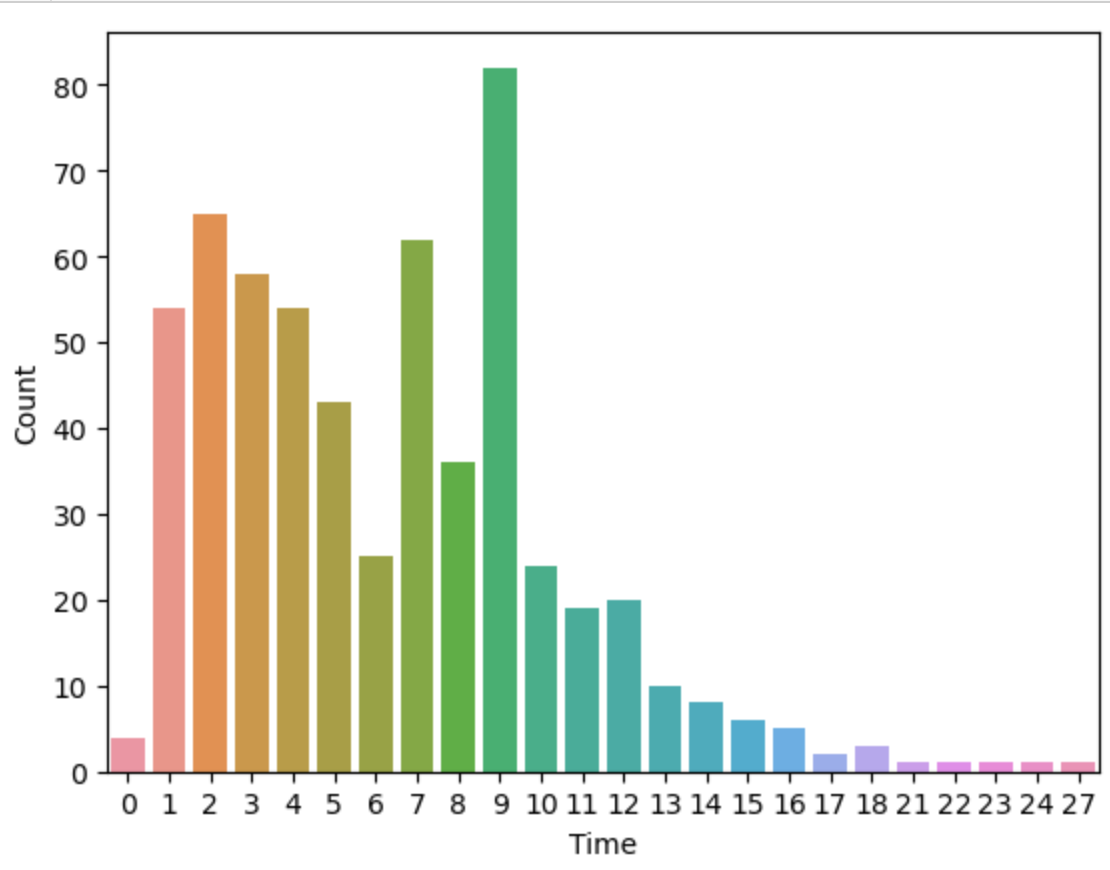
Подавляющее большинство записей имеют длину 9 секунд, но встречаются и другие длительности в диапазоне от 0 до 27 секунд. Также есть записи с 0 длительностью, их уберем из нашего датасета.
Подготовка данных
Мы не можем использовать необработанный аудиосигнал в качестве входных данных для наших будущих моделей. Для работы с аудиосигналом его необходимо оцифровать, то есть преобразовывать звуковую волну в ряд чисел. Благодаря дискредитации звука из аудио можно извлекать достаточно большое число различных характеристик. Например, такие как мел-кепстральный коэффициенты (MFCCs), спектр, спектральный центроид (Spectral Centroid), спектральный спад (Spectral Rolloff), скорость пересечения нуля и так далее.
MFCC или мел-кепстральные коэффициенты являются широко используемым методом извлечения характеристик из аудиосигнала. В этом нам поможет библиотека librosa, с помощью которой будем обрабатывать наши аудиосигналы.
У нас имеется 563 размеченных аудиофайла для обучения наших моделей. Расширим этот набор данных за счет генерации синтетических данных. Будем использовать методы растяжения и сужения звукового сигнала во времени. Таким образом у нас каждый аудиосигнал будет иметь 3 формы, что сделает наш классификатор более устойчивым и поможет в правильной классификации сердечных ритмов. В качестве основных характеристик аудиосигнала будем вычислять мел-кепстральные коэффициенты. Проделаем следующие шаги для обработки наших записей сердечных тонов.
Преобразуем аудиофайлы в файлы с одинаковой длительностью. Для этого будем использовать метод
librosa.util.fix_length().Увеличим наш набор данных, применяя методы растяжения и сужения звукового сигнала с коэффициентами 1.2 и 0.8 соответственно с помощью метода
librosa.effects.time_stretch().Извлечем мел-кепстральные коэффициенты с помощью метода
librosa.feature.mfcc()для каждого аудиофайла и посчитаем среднее по каждому коэффициенту.
Напишем функцию, которая будет обрабатывать аудиофайлы.
def load_file_data (folder, file_names, duration=9, sr=22050):
input_length=sr*duration
features = 52
data = []
for file_name in file_names:
try:
sound_file = folder+file_name
X, sr = librosa.load( sound_file, sr=sr, duration=duration)
dur = librosa.get_duration(y=X, sr=sr)
# меням длительность
if (round(dur) < duration):
print ("fixing audio lenght :", file_name)
X = librosa.util.fix_length(data=X, size=input_length)
# извлекаем mfcc коэффициенты, используя 52 характеристики
mfccs = np.mean(librosa.feature.mfcc(y=X, sr=sr, n_mfcc=features).T,axis=0)
featuress = np.array(mfccs).reshape([-1,1])
data.append(featuress)
# сужаем уадиосигнал с коэффициентом 0.8
squeeze_data = librosa.effects.time_stretch(y=X, rate=0.8)
mfccs_squeeze = np.mean(librosa.feature.mfcc(y=squeeze_data, sr=sr, n_mfcc=features).T,axis=0)
feature_1 = np.array(mfccs_squeeze).reshape([-1,1])
data.append(feature_1)
# растягиваем сигнал с коэффициентом 1.2
stretch_data = librosa.effects.time_stretch(y=X, rate=1.2)
mfccs_stretch = np.mean(librosa.feature.mfcc(y=stretch_data, sr=sr, n_mfcc=features).T,axis=0)
feature_2 = np.array(mfccs_stretch).reshape([-1,1])
data.append(feature_2)
except Exception as e:
print("Error encountered while parsing file: ", file_name)
return data
И обработаем все файлы, содержащиеся в папках: normal, murmur, artifact, axtrastole, создав при этом массив в метками.
max_duration=9
artifact_files = fnmatch.filter(os.listdir(artifact_data), 'artifact*.wav')
artifact_sounds = load_file_data (folder=artifact_data, file_names = artifact_files, duration=max_duration)
artifact_labels = [0 for items in artifact_sounds]
murmur_files = fnmatch.filter(os.listdir(murmur_data), 'murmur*.wav')
murmur_sounds = load_file_data(folder=murmur_data,file_names=murmur_files, duration=max_duration)
murmur_labels = [1 for items in murmur_sounds]
extrastole_files = fnmatch.filter(os.listdir(extrastole_data), 'extrastole*.wav')
extrastole_sounds = load_file_data(folder=extrastole_data,file_names=extrastole_files, duration=max_duration)
extrastole_labels = [2 for items in extrastole_sounds]
normal_files = fnmatch.filter(os.listdir(normal_data), 'normal*.wav')
normal_sounds = load_file_data(folder=normal_data,file_names=normal_files, duration=max_duration)
normal_labels = [3 for items in normal_sounds]
Далее определим метки классов.
classes= ['artifact','murmur','extrastole','normal']
labels = {k:v for v,k in enumerate(classes)}
{'artifact': 0, 'murmur': 1, 'extrastole': 2, 'normal': 3}Теперь можно собрать все данные и разделить выборку на обучающую, тестовую и валидационную.
x_data = np.concatenate((artifact_sounds, normal_sounds,murmur_sounds,extrastole_sounds))
y_data = np.concatenate((artifact_labels, normal_labels,murmur_labels,extrastole_labels))
from sklearn.model_selection import train_test_split
# shuffle - whether or not to shuffle the data before splitting. If shuffle=False then stratify must be None.
# split data into Train, Validation and Test
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, train_size=0.8, random_state=42, shuffle=True)
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, train_size=0.9, random_state=42, shuffle=True)
Теперь у нас есть обработанные данные, разделенные на выборки для обучения, тестирования и валидации, можем приступать к построению моделей.
Начнем с классических моделей машинного обучения. Алгоритм «случайный лес» (RandomForest, RF) у специалистов по обработке данных является одним из самых популярных и надежных методов в задачах классификации. Модель имеет много параметров, настройка которых может существенно повлиять на конечный результат, поэтому переберем некоторые комбинации параметров и выберем один с лучшей оценкой.
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
forest_grid_search = GridSearchCV(RandomForestClassifier(), {
'n_estimators': [300,400,500,700,800,1000],
'max_features': ['sqrt','log2'],
'max_depth': [3,5,7,9,11,13,15,17,19,21],
'bootstrap': [True, False]},cv=3,verbose=1, n_jobs=-1 )
forest_grid_search.fit(X_train,y_train)Посмотрим на параметры лучшей модели
forest_grid_search.best_params_
{'bootstrap': False,
'max_depth': 19,
'max_features': 'sqrt',
'n_estimators': 800}Оценим теперь точность и эффективность нашей модели, чтобы понять насколько хорошо она работает в разных классах, построив отчет classification report.
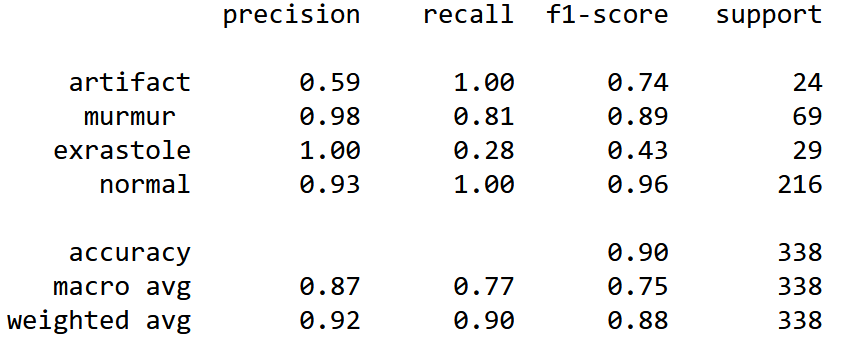
Рассчитав точность алгоритма, получим 0.89645. Значение точности получилась достаточно неплохое, но мы видим, что у алгоритма есть проблемы с классами artifact и extrastole. Низкий recall у класса extrastole говорит о том, что алгоритму случайного леса тяжело обнаружить данный класс вообще. Класс artifact алгоритм может обнаружить, но плохо отличает от других классов.
Теперь рассмотрим алгоритм градиентного бустинга XGBoost и тоже попробуем настроить его параметры.
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
from xgboost import XGBClassifier
from scipy import stats
xgb_grid_search = GridSearchCV(XGBClassifier(), {
'n_estimators':[200,300,400,500,700,800,900,1000],
'max_depth': [3,4,5,6,7,9,11,13,15,17,19,21]},verbose=3, n_jobs=-1 )
xgb_grid_search.fit(X_train,y_train)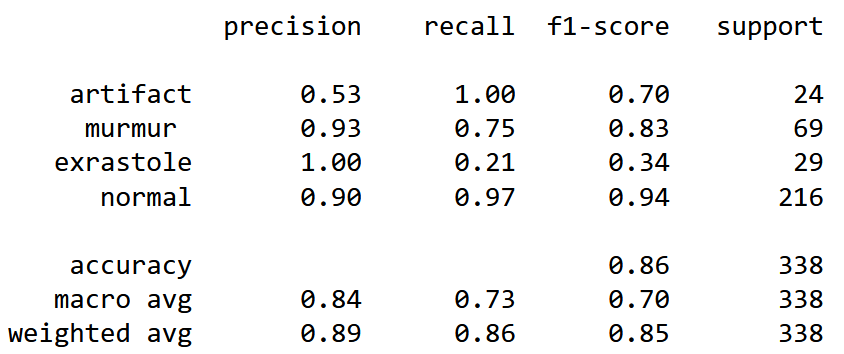
Рассчитав точность, получим 0.85207, что даже немного ниже, чем точность алгоритма случайного леса. И алгоритм также тяжело справляется с классами artifact и extrastole. Но при этом видно, что оба алгоритма путают болезни между собой, но хорошо справляются вообще с обнаружение или не обнаружением болезней.
В качестве нейронной сети возьмем сочетание сверточной сети и сети LSTM. С нейронными сетями наверное интереснее, так как на вход мы можем подавать как характеристики, извлеченные из аудиосигнала и использовать их для классификации, так и, например, спектрограммы, которые мы можем сформировать для каждого сигнала, тем самым преобразовав задачу классификации звука в задачу классификации изображений. Но так как мы сравниваем алгоритмы между собой, то на вход нейронной сети также будем подавать мел-кепстральные коэффициенты, извлеченные из аудиосигнала.
Попробуем скорректировать несбалансированность в наборе данных с помощью взвешивания классов. Для этого определим веса для каждого класса.
# class weight
train_count = 563
count_0 = 40 #artifact
count_1 = 127 #murmur
count_2 = 46 #extrastole
count_3 = 350 #normal
weight_for_0 = train_count / (4 * COUNT_0)
weight_for_1 = train_count / (4 * COUNT_1)
weight_for_2 = train_count / (4 * COUNT_2)
weight_for_3 = train_count / (4 * COUNT_3)
class_weight = {0: weight_for_0, 1: weight_for_1, 2: weight_for_2,3: weight_for_3}
{0: 3.5375,
1: 1.0968992248062015,
2: 3.0760869565217392,
3: 0.4031339031339031}Модель нейронной сети имеет 3 блока с несколькими сверточными слоями (Conv1D), слоями максимального объединения (MaxPooling1D) и слоями BatchNormalization, которые нормализуют данные перед каждым входом в слой, 2 полносвязных слоя (Dense) со слоями Dropout для предотвращения переобучения модели и выходной слой с 4 выходами в соответствии с количеством классов эмоций. Выходной слой имеет активационную функцию softmax, так как она возвращает распределение вероятностей по целевым классам в задаче многоклассовой классификации. Во всех сверточных слоях используется активационная функция relu.
lstm_model = Sequential()
lstm_model.add(Conv1D(1024, kernel_size=5, strides=1, padding='same', activation='relu', input_shape=(52, 1)))
lstm_model.add(MaxPooling1D(pool_size=2, strides = 2, padding = 'same'))
lstm_model.add(BatchNormalization())
lstm_model.add(Conv1D(512, kernel_size=5, strides=1, padding='same', activation='relu'))
lstm_model.add(MaxPooling1D(pool_size=2, strides = 2, padding = 'same'))
lstm_model.add(BatchNormalization())
lstm_model.add(Conv1D(256, kernel_size=5, strides=1, padding='same', activation='relu'))
lstm_model.add(MaxPooling1D(pool_size=2, strides = 2, padding = 'same'))
lstm_model.add(BatchNormalization())
lstm_model.add(LSTM(128, return_sequences=True))
lstm_model.add(LSTM(128))
lstm_model.add(Dense(64, activation='relu'))
lstm_model.add(Dropout(0.3))
lstm_model.add(Dense(32, activation='relu'))
lstm_model.add(Dropout(0.3))
lstm_model.add(Dense(4, activation='softmax')) #4 класса для классификации
lstm_model.summary()Определим оптимизатор Адама, настроим шаг обучения, установим функцию потерь и скомпилируем модель.
optimiser = tf.keras.optimizers.Adam(learning_rate = 0.0001)
lstm_model1.compile(optimizer=optimiser,
loss='categorical_crossentropy',
metrics=['accuracy'])
cb = [EarlyStopping(patience=20,monitor='val_accuracy',mode='max',restore_best_weights=True)]Запускаем обучение нашей сети, не забыв указать веса для каждого класса и точку для ранней остановки.
history = lstm_model.fit(x_train, y_train,
validation_data=(x_val, y_val),
batch_size=8, epochs=250,
class_weight=class_weight,callbacks = cb )По окончании обучения построим отчет.
from sklearn.metrics import classification_report
classes = ["artifact" ,"murmur ", 'exrastole', "normal"]
preds = lstm_model.predict(x_test)
classpreds = [ np.argmax(t) for t in preds ]
y_testclass = [np.argmax(t) for t in y_test]
print(classification_report(y_testclass, classpreds, target_names=classes))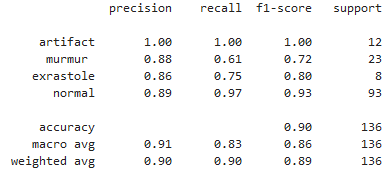
Рассчитав точность нашей нейросетевой модели на валидационной выборке, получим 0,9438. Видим, что наша нейронная сеть очень хорошо справилась с задачей. И она значительно лучше справляется с распределением по классам artifact и extrastole.
Давайте подведем итоги. Скорее всего, если немного еще поработать с выборкой, может поработать со спектрограммой, может расширить набор признаков, увеличить набор датасета, изменить параметры нейронной сети, то мы получим еще более лучший результат. Считаю, что в дальнейшем стоит поработать с построенной моделью нейронной сети и рассмотреть другие методы для устранения дисбаланса классов для получения более точных показателей.
Кстати, у моих коллег из OTUS скоро пройдет бесплатный вебинар про уникальный эксперимент, который начался в 2020-м году в Москве, где городские поликлиники подключены к единой базе данных, а тысячи рентгенограмм ежедневно анализируются искусственным интеллектом. Регистрируйтесь, будет интересно!
