Об удалении тренда из экспериментальных данных
При анализе экспериментально полученных стационарных временных рядов, как правило, при предварительной подготовке (препроцессинге) данных возникает необходимость в подавлении имеющегося в них тренда.
Здесь будет предложен «новый» метод выделения тренда — простой, очевидный и пригодный для очень сложных видов тренда.
Под трендом обычно понимают сверхнизкочастотную негармоническую компоненту, резко нарушающую стационарность процесса. Наиболее частой причиной тренда в экспериментально полученных данных является «дрейф нуля» регистрирующей аппаратуры. Интегрирование данных и некоторые другие виды обработки также могут стать причиной появления тренда. Наличие тренда сильно искажает результаты последующей обработки данных (спектральное оценивание и т.п.), поэтому удаление тренда является необходимым. В ряде случаев сам тренд является ценным источником информации (например, при анализе долгосрочных тенденций в экономических или метео- процессах).
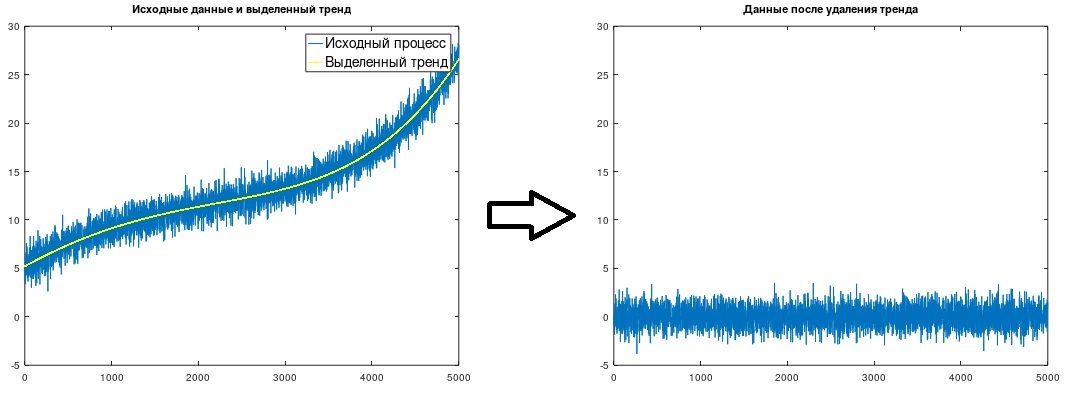
Рис. 1. Выделение и удаление тренда
Обычно тренд моделируют с помощью линейных или степенных (2-го или 3-го порядка) функций, коэффициенты которых вычисляют, умножая процесс на определенные последовательности и применяя затем довольно сложные формулы, выведенные на основании метода наименьших квадратов. (см., например, Дж.Бендат, А. Пирсол, «Прикладной анализ случайных данных», М., Мир, 1989.) Ниже предлагается несколько модифицированный метод, также основанный на методе наименьших квадратов, который очень прост в понимании и освоении, и не требует ни обращения к справочникам, ни самостоятельных сложных символьных выкладок для получения необходимых зависимостей, при этом позволяет моделировать тренд функциями любого вида. Этот модифицированный метод настолько прост и очевиден (освоив однажды, скрипты можно потом писать по памяти), что наверняка уже не раз «изобретался» разными исследователями, но мне пока что-то не попадался ни в каких источниках.
Для выделения тренда производится аппроксимация исходного процесса x[i], состоящего из N+1 отсчетов, с помощью малого количества k составляющих тренд функций uj[i]: 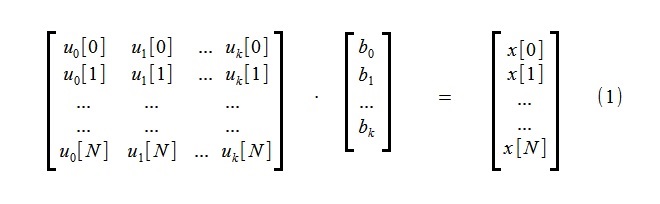
(Обычно в качестве функций uj[i] выбирают степенные функции,

но для данного метода это абсолютно непринципиально)
Система линейных алгебраических уравнений (1) включает k неизвестных bj и N+1 уравнений.
Принимая обозначения:

записываем более компактно

Применение метода наименьших квадратов при поиске приближенного решения переопределенной системы, в матричной форме записывается так:

При написании скрипта: Естественно, никакой необходимости хранить целиком большую матрицу U нет, элементы матрицы UT U и вектора UTx можно «накапливать» пошагово.
Система (4) из k уравнений и k неизвестных решается очевидными методами -ну, например, запишем так:

после чего, по найденным bj, можно построить тренд θ[i] в виде
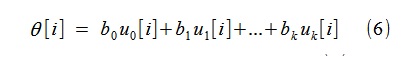
Для примера был смоделирован случайный процесс x[i] вида
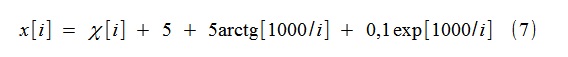
где χ[i]- гауссов белый шум с единичной дисперсией. Тренд смоделирован функциями типа (2) (точнее,(8)), до 4-го порядка включительно (k=4).
При использовании для моделирования тренда степенных функций следует заметить, что матрица UT U (4) теоретически всегда обратима в силу линейной независимости этих функций, однако при высоких порядках k (либо очень длинных реализациях N, что менее критично) определенные ее элементы могут быть очень велики по абсолютной величине. При высоких порядках k в случае вычислительных затруднений рекомендуется использовать понижающие коэффициенты, например, такие (8):

(Δt=1), что и было сделано в рассмотренном примере. Получен тренд, показанный на рис. 1.
После выделения тренда его, естественно, следует просто вычесть из исходных данных.
Замечание. Обычно авторитетные источники не рекомендуют работать с моделями тренда порядка выше k=2 (квадратной параболы). Связано ли это со сложностью определения «амплитудных» коэффициентов bj традиционными методами, или с упомянутым выше исчерпанием порядков машинных переменных, или с ложным отнесением к тренду информативных составляющих процесса, не очень понятно. В приведенном примере тренд 4-го порядка выделен вроде бы довольно правдоподобно (правда, не намного отличаясь от тренда 3-го порядка). Для особо сложных случаев источники рекомендуют использовать иной метод — низкочастотную фильтрацию (здесь не рассматривался).
Выделение тренда, как показано выше — процедура не столь уж и сложная, позволяет либо выделить и проанализировать «медленные» тенденции, либо, что чаще, помогает получить «на выходе» качественные данные — центрированный стационарный случайный процесс, пригодный для дальнейшего анализа.
