О существовании периодических решений в системе Лоренца
 Это третий мой топик на Хабре (часть 1 и часть 2), посвященный динамической системе Лоренца. Я продолжаю заниматься исследованием вопроса о существовании периодических решений (циклов) в этой системе. Удалось получить интересный результат при определенном соотношении ее параметров.Рассмотрим систему дифференциальных уравнений Лоренца
Это третий мой топик на Хабре (часть 1 и часть 2), посвященный динамической системе Лоренца. Я продолжаю заниматься исследованием вопроса о существовании периодических решений (циклов) в этой системе. Удалось получить интересный результат при определенном соотношении ее параметров.Рассмотрим систему дифференциальных уравнений Лоренца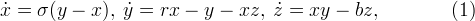 где
где 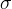 , r и b — некоторые положительные числа, параметры системы.
, r и b — некоторые положительные числа, параметры системы.
Докажем, что если 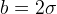 , то в системе (1) нет периодических решений (исключая, конечно, положения равновесия).
, то в системе (1) нет периодических решений (исключая, конечно, положения равновесия).
Сделаем замену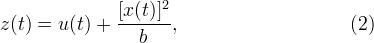 где u (t) — некоторая функция от времени.
где u (t) — некоторая функция от времени.
Продифференцируем (2), получим
В левую часть выражения (3) подставим правую часть третьего уравнения системы (1), а в правую часть (3) — правую часть первого уравнения системы (1), учитывая, что 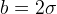 . Получим
. Получим
Вместо z в (4) подставим выражение (2), откуда имеем уравнение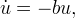 решением которого является функция
решением которого является функция где
где 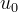 — произвольная постоянная.
— произвольная постоянная.
Теперь во второе уравнение системы (1) подставим вместо z выражение (2). При этом выразим y из первого уравнения системы (1). Получим и
и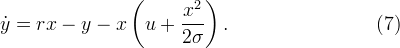
Подставив (5) и (6) в (7), имеем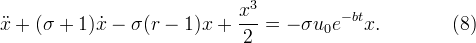
Рассмотрим неавтономный случай, когда 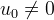 в уравнении (8). Предположим, что в этом случае уравнение (8) имеет периодическое решение с периодом T. Так как производная периодической функции с периодом T есть периодическая функция с периодом T, то левая часть уравнения (8) является периодической функцией с периодом T. Однако правая часть уравнения (8) непериодична, так как
в уравнении (8). Предположим, что в этом случае уравнение (8) имеет периодическое решение с периодом T. Так как производная периодической функции с периодом T есть периодическая функция с периодом T, то левая часть уравнения (8) является периодической функцией с периодом T. Однако правая часть уравнения (8) непериодична, так как 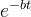 не является периодической функцией. Получили противоречие.
не является периодической функцией. Получили противоречие.
Таким образом, при 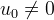 уравнение (8) не имеет периодических решений.
уравнение (8) не имеет периодических решений.
Рассмотрим теперь случай, когда  . Имеем автономное уравнение второго порядка
. Имеем автономное уравнение второго порядка у которого по критерию Бендиксона [1, с. 142–143] нет периодических решений, что и доказывает их отсутствие в системе Лоренца при
у которого по критерию Бендиксона [1, с. 142–143] нет периодических решений, что и доказывает их отсутствие в системе Лоренца при 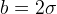 .
.
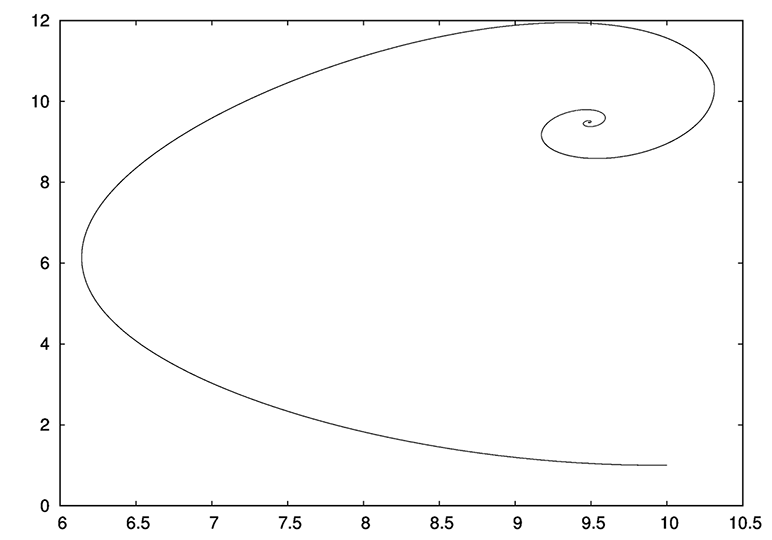
Заметим, что в этом случае параметр r может принимать любые значения. Тогда при достаточно больших его значениях в системе Лоренца также будут отсутствовать периодические решения, что кажется весьма неочевидным, поскольку параметр r пропорционален разности температур между нижним и верхним слоем жидкости при свободной конвекции. При увеличении градиента температуры в слое должны возникнуть в жидкости конвективные валы, а здесь жидкость со временем приходит в стационарное состояние (ламинарный режим). Это подтверждается и в численном эксперименте (наблюдались устойчивые фокусы при разных значениях r — рисунок (проекция дуги траектории на плоскость xOy) в начале топика). Скорее всего, это объясняется тем, что система Лоренца достаточно грубо описывает данный процесс, хотя при других соотношениях между  и b (r принимает достаточно большое значение) в системе (1) наблюдается устойчивый предельный цикл [2, с. 291–294].
и b (r принимает достаточно большое значение) в системе (1) наблюдается устойчивый предельный цикл [2, с. 291–294].
Несмотря на всю простоту, на мой взгляд, данный результат с точки зрения теории дифференциальных уравнений интересен тем, что нелинейная система третьего порядка допустила понижение порядка, что редко бывает, а теория дифференциальных уравнений на плоскости достаточно хорошо проработана.
Рассмотрим другой случай, когда 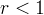 . В известной мне литературе он исследуется в линейном приближении. Применим второй метод Ляпунова. Составим функцию Ляпунова
. В известной мне литературе он исследуется в линейном приближении. Применим второй метод Ляпунова. Составим функцию Ляпунова обладающую свойствами:
обладающую свойствами: 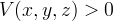 для
для 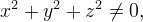
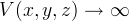 при
при 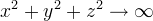 и
и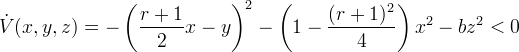 для
для 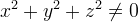 в силу правых частей уравнений системы (1). Тогда по теореме Барбашина-Красовского [3, с. 248–250] любое решение системы (1)
в силу правых частей уравнений системы (1). Тогда по теореме Барбашина-Красовского [3, с. 248–250] любое решение системы (1)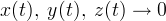 при
при 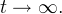
Более общий случай описан в работе [4] (лемма 1.2), где доказывается отсутствие циклов в системе (1) (предельные режимы — положения равновесия) для и
и 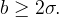
Также отметим, что у системы (1) всегда есть частные решения вида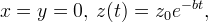 где
где 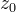 — произвольная постоянная.
— произвольная постоянная.
В данном топике был рассмотрен вопрос отсутствия у системы (1) периодических решений. Однако аналитические исследования динамики системы (1) на наличие циклов описаны в литературе, но источников не так много, поскольку многие изучают систему Лоренца численно. Далее приведен список литературы, где удалось найти строгое доказательство существования предельного цикла в системе (1) при больших значениях параметра r [2, 4–8]. В него входит рукопись [4] Виктора Иосифовича Юдовича (неизданная ранее в научных журналах), где подробно освещен этот вопрос.
Литература1. Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. — М.: Едиториал УРСС, 2004.2. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. — М: ЛИБРОКОМ, 2009.3. Демидович Б.П. Лекции по математической теории устойчивости. — М.: Наука, 1967.4. Юдович В.И. Асимптотика предельных циклов системы Лоренца при больших числах Рэлея // Рукопись деп. в ВИНИТИ, №2611–78. 1978.5. Robbins K.A. Periodic Solutions and Bifurcation Structure at High R in the Lorenz Model // SIAM Journal on Applied Mathematics, 36(3): 457–472, 1979.6. Shimizu T. Analytic Form of the Simplest Limit Cycle in the Lorenz Model // Physica A: Statistical Mechanics and its Applications, 97(2): 383–398, 1979. DOI: 10.1016/0378–4371(79)90113–4.7. Покровский Л.А. Решение системы уравнений Лоренца в асимптотическом пределе большого числа Релея. I. Система Лоренца в простейшей квантовой модели лазера и приложение к ней метода усреднения // Теоретическая и математическая физика, 62(2): 272–290, 1985.8. Jibin Li, Jianming Zhang. New Treatment on Bifurcations of Periodic Solutions and Homoclinic Orbits at High r in the Lorenz Equations // SIAM Journal on Applied Mathematics, 53(4): 1059–1071, 1993.
