О разложении многоканального отклика системы по «псевдособственным» формам колебаний
Обклеенный десятками датчиков «объект исследований» при натурных динамических испытаниях (например, при исследовании виброактивности транспортного средства) легко обеспечивает нас большим объемом полученных данных, но вот что с ними делать, зачастую не очень-то ясно. То же самое — при симуляционом моделировании динамических процессов систем с большим количеством степеней свободы. Это может быть не совсем понятно тем, кто не сталкивается с проблемой регулярно, но — отсматривать соответствующую анимацию процесса, стохастического во времени и пространстве, как правило, почти бессмысленно. Где сломается или почему так трясет — обычно «не видно». Что придумывали кроме анимации, ниже расскажу, а порекомендую вот что. Путем элементарнешей процедуры можно получить и сами пространственные «формы» колебаний, причем именно реально проявляющиеся в данных условиях нагружения, и интенсивности их проявления (дисперсии; при желании — и сами процессы).
| Исходный многоканальный процесс
|
Разложение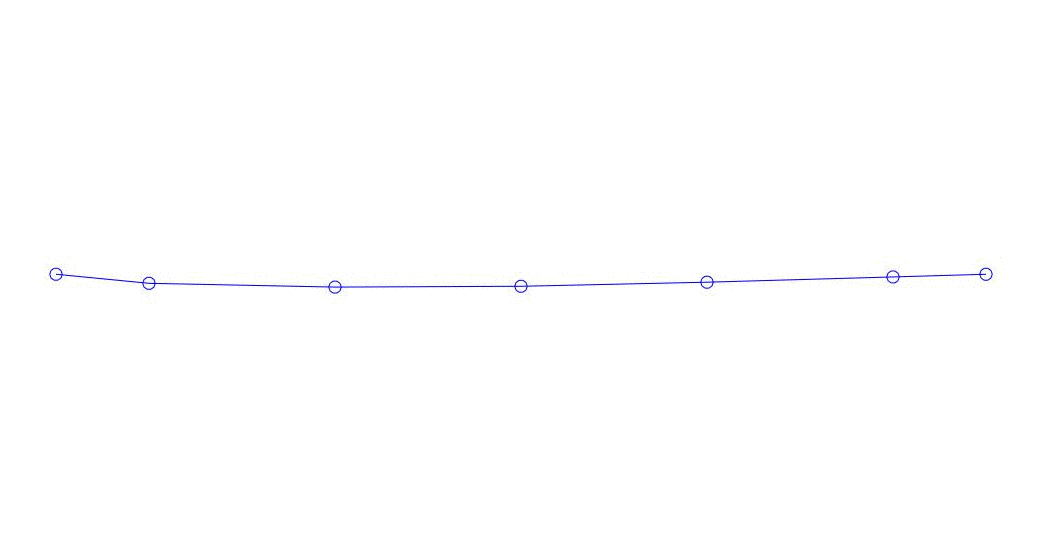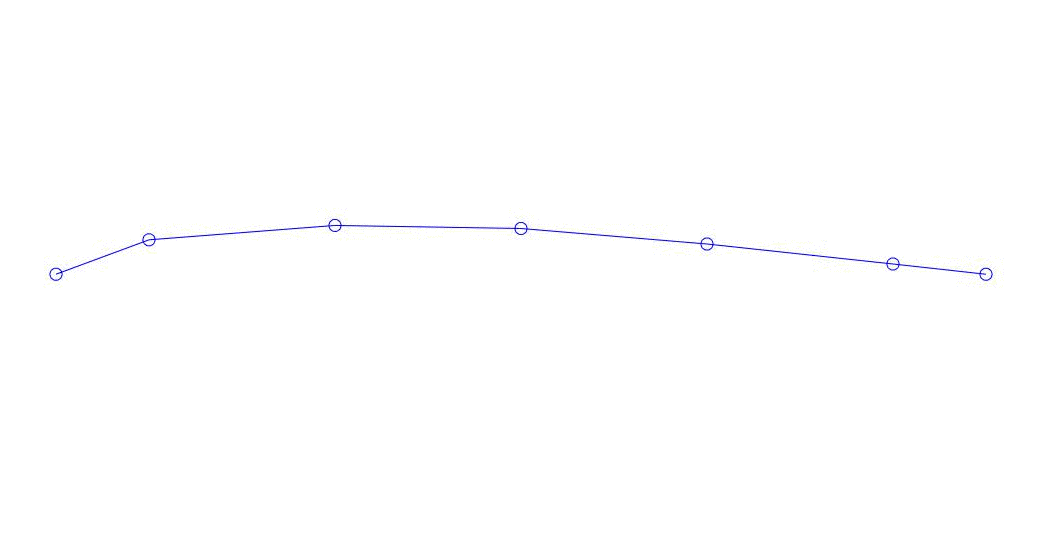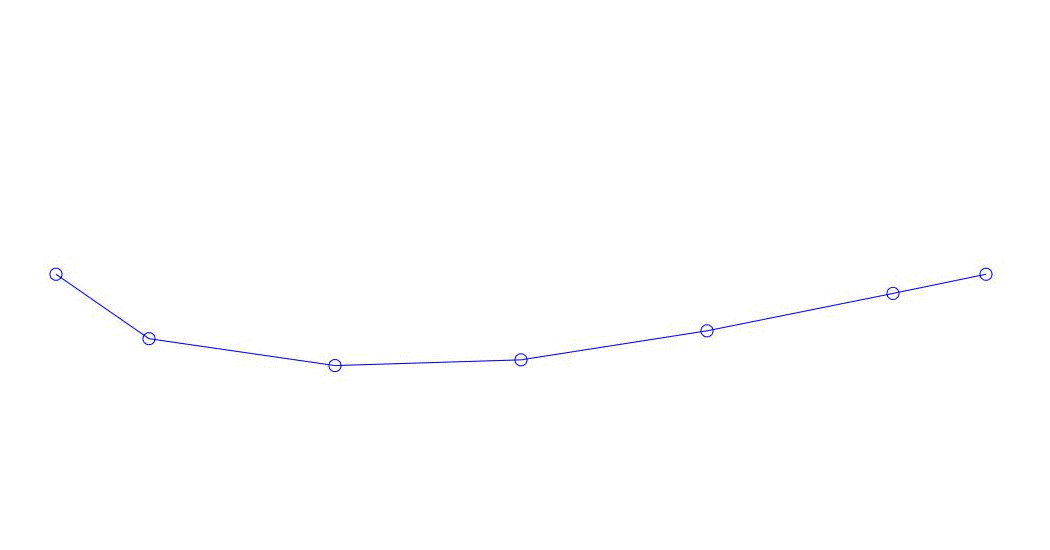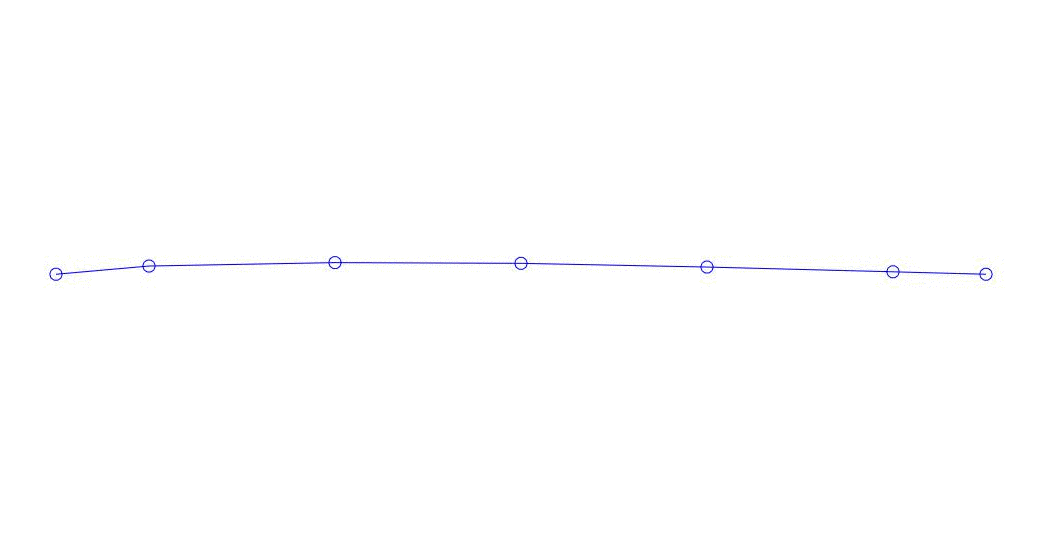 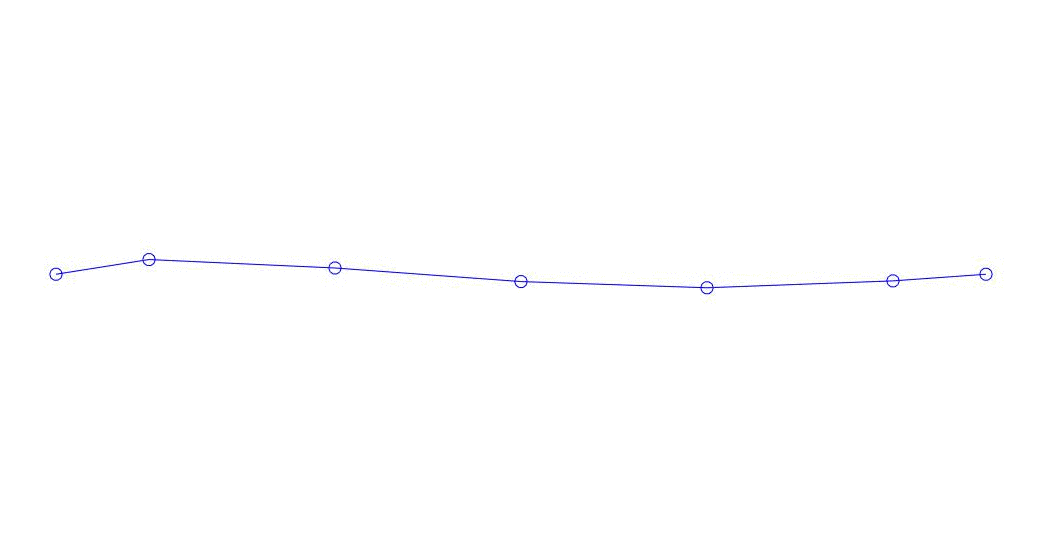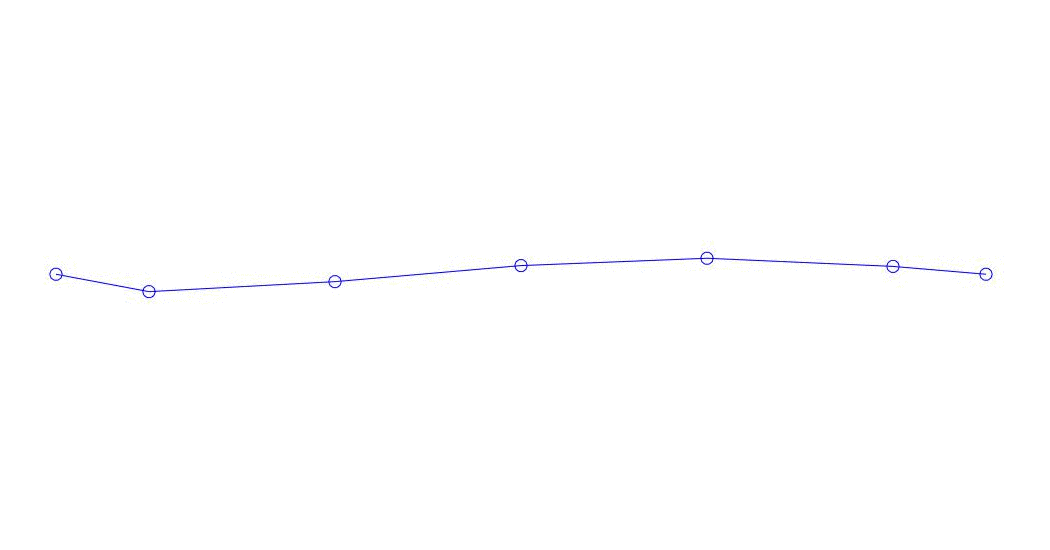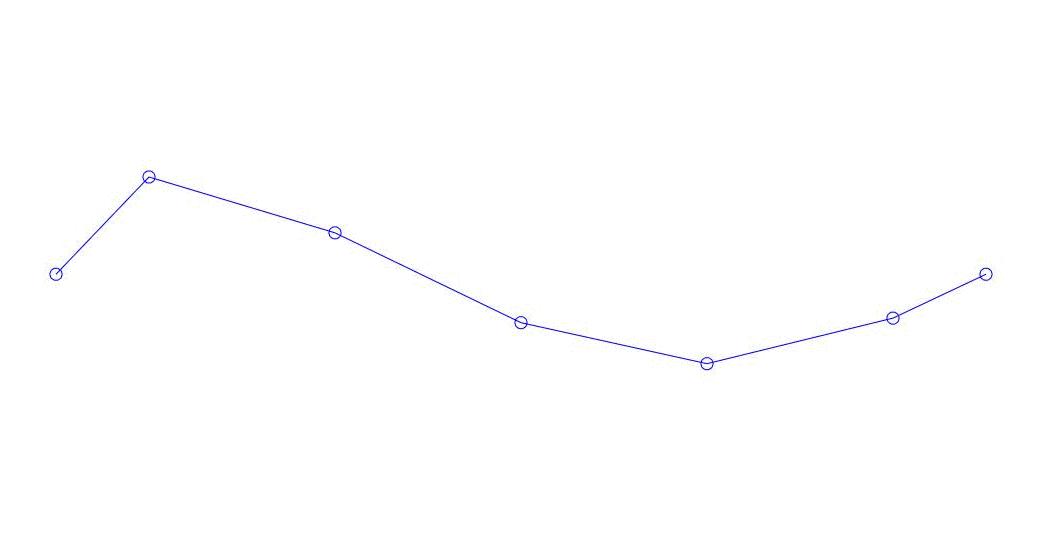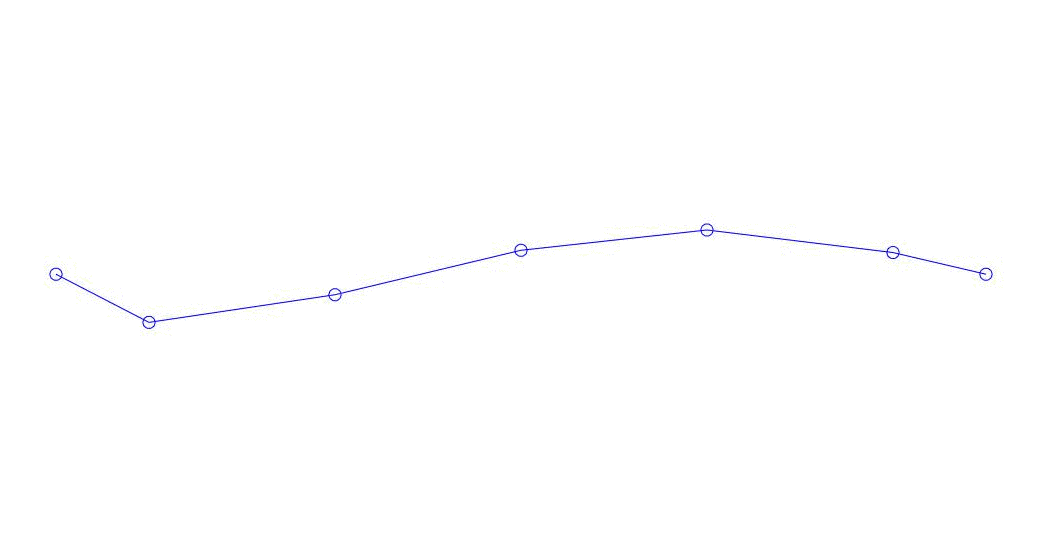 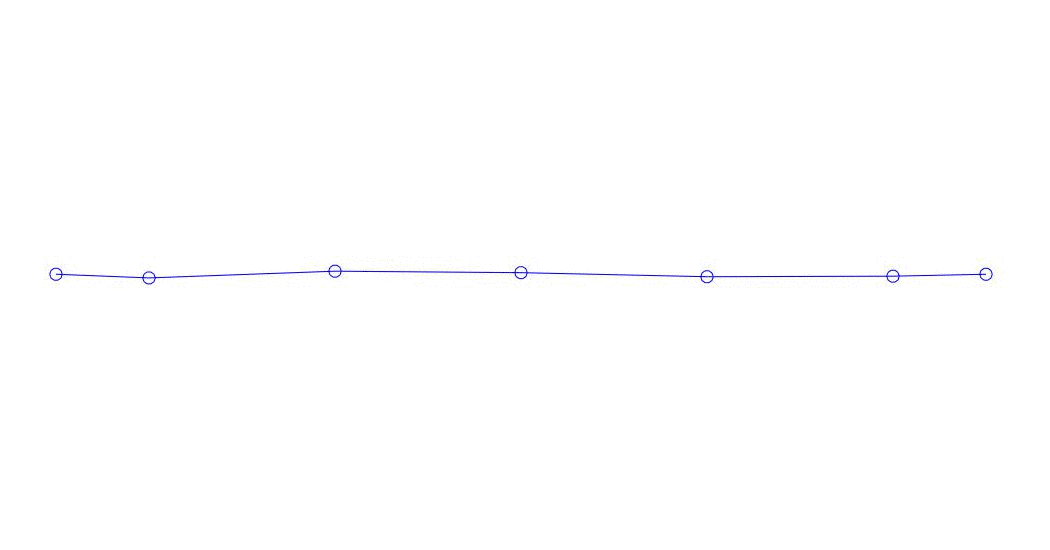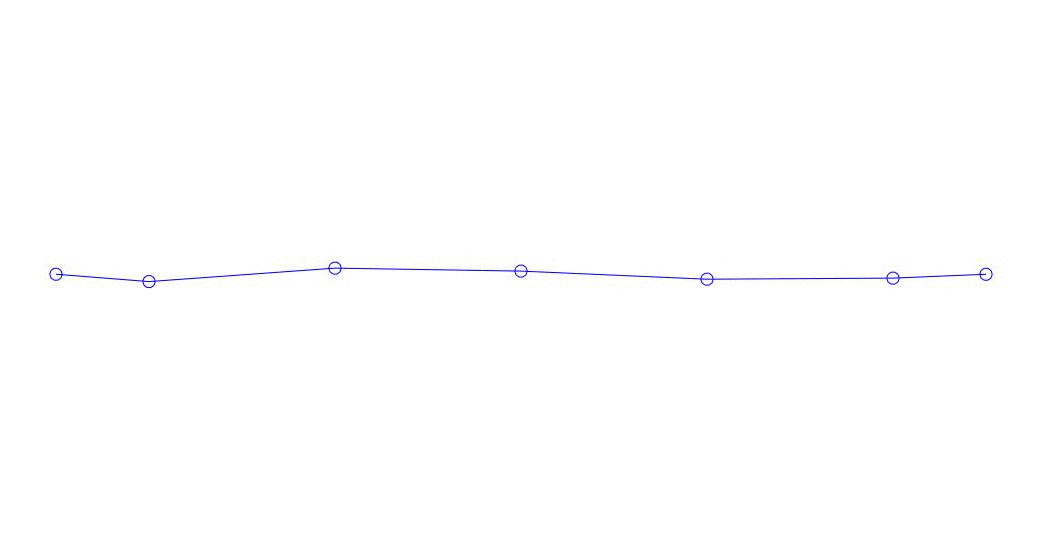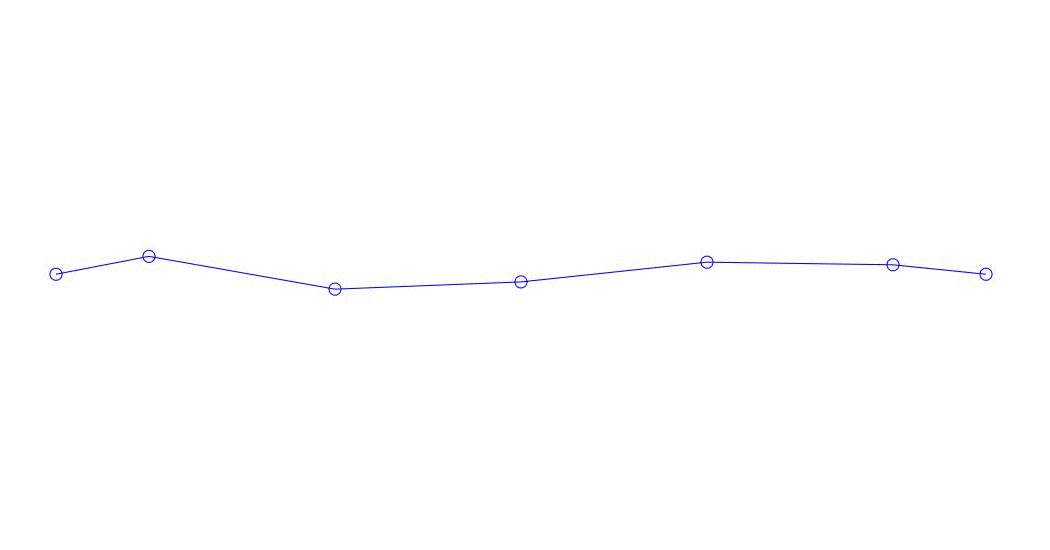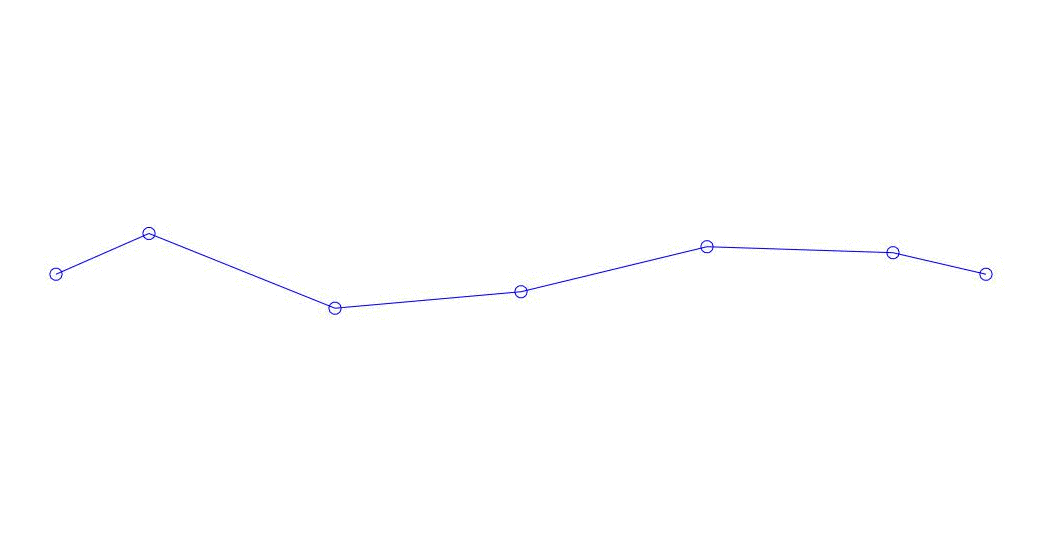 |
Рис. 1 Разложение многоканального отклика по псевдоформам. «Струна в вязкой среде»(см.рис. 2)
Кроме анимации, известны «попарные» исследования (взаимные спектры и т.д), которые общей картины, естественно, не дают.
Довольно очевидны такие способы — «вырезанием» очень узких полос спектра, соответствующих резонансным пикам на спектрограммах, спектрограммным (опять же «попарным») путем получают почти-формы почти-гармонических (высококоррелированных) колебаний. Кроме очевидной технической сложности, недостаток таких способов в том, что обычно надо «удачно» выбрать «опорный» канал, что не всегда возможно — как следствие, возникают очень большие ошибки во взаимных фазах процессов, кроме того, выделенная пространственная форма колебаний и без таких ошибок в силу свойств линейной системы может оказаться «комплексной» (несинфазной), что ее ценность для последующего субъективного анализа обычно (не всегда) ощутимо снижает.
Известно 4-канальное исследование крутильных колебаний (несущей системы среднего автобуса), выделяемых в один процесс фактически с помощью пространственной формы колебаний, определенной по наитию исследователя — показания двух датчиков, расположенных диагонально по углам кузова, складывались (брались с »+»), из них вычитались (брались с »-») показания двух других, расположенных осесимметрично. Даже при малом количестве датчиков такой подход может быть не совсем хорош. Например, рама грузового автомобиля обычно существенно более податлива в подмоторной (передней) части, соответственно, крутильную форму, возможно, следовало предполагать в более сложном виде (наверное, с какими-то «повышающими» коэффициентами для передних датчиков — и одновременно обостряется вопрос обоснования принятой модели). При большем числе каналов наблюдения все это совсем уж сложно и плохо обосновано.
Явное выделение (в отдельные процессы) нескольких форм колебаний (мод), заранее определенных из иного эксперимента или моделирования, когда-то мною (наверное, не только мною) предлагалось и было непосредственным моим шефом обозвано тогда «методом модальной декомпозиции». Предполагалось так анализировать результаты полигонных испытаний, а вектора собственных форм определять стендовыми испытаниями (либо конечноэлементным моделированием).
Собственно, примерно это и делали, но одновременно выяснилось вот что.
Понятно, что «стендовым экспериментаторам», в отличие от «полигонных», доступен для синхронного наблюдения истинный возмущающий процесс. Это давало им большое преимущество — можно было определить истинные передаточные функции и использовать имевшиеся аппаратно-программные средства для экспериментального определения собственных форм и частот колебаний конструкции (на основании курвфиттинга, с «вырезанием» «на глаз» частотных диапазонов и указанием системе, сколько там форм найти; тоже скорее искусство, чем наука, но все-таки). Однако. Объект типа автомобиля в сборе они явно избегали исследовать, предпочитая отдельные рамы, несущие кузова и т.п. — объекты с очень малым демпфированием. Речь именно о модальных стендовых испытаниях — определении собственных частот и форм. Не о симуляционных. Правдоподобные собственные формы колебаний на чуть более сильно задемпфированных объектах эспериментально получить в принципе можно, но ощутимо сложнее.
Весьма ценная информация оказалась, об этих «предпочтениях». Если очень-очень коротко — только выводы, к которым удалось впоследствии постепенно прийти: стремиться разложить отклик именно на истинные собственные формы конструкции вряд ли стОит, несмотря на «красивость» идеи.
Если «на пальцах», то причина, по видимому, с высокой вероятностью, такая — в зависимости от внешнего возмущения, «собственные формы колебаний» (точнее, стационарные «модальные» процессы, соответствующие собственным формам колебаний), скорее всего, будут так или иначе коррелированы между собой, фактически образуя какие-то иные пространственные формы колебаний, в той или иной степени отличные от собственных, и проявляется это, естественно, в сильной зависимости от задемпфированности конструкции — как краткое пояснение «от противного» — две разных «незатухающих» гармоники некоррелированы, само собой, всегда никак. (Пояснение. Упомянутый эффект «смешивания собственных форм» наблюдается и в отсутсвии «существенных нелинейностей», и вне случаев «комплексных форм» при «непропорциональном» демпфировании в линейных системах.)
Исходя из изложенного, предлагается представить отклик системы как сумму нескольких корреляционно-независимых процессов типа неких форм колебаний (изгибных, крутильных и т.п.). Такой анализ очень прост, как правило, дает очень ценные результаты. Полученные формы могут быть сходны с собственными формами колебаний системы, а могут и нет, но всегда отражают поведение системы именно в условиях реального внешнего воздействия. причем отражают максимально просто и информативно, а их ранжированная по их дисперсиям последовательность представляет собой аппроксимирующий ряд.
Для получения интересующего нас разложения рассматривается (1),
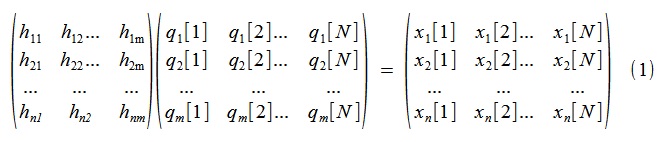
или, то же, компактно, (2),
| Hq = x (2) |
где x — непосредственно полученный в эксперименте n-канальный физический отклик системы длительностью N отсчетов, q — m-канальный действительный «модальный» процесс со взаимно некоррелированными каналами, H — матрица из столбцов, описывающих искомые синфазные («действительные») формы колебаний.
Вообще говоря, впоследствии ожидается m
| H·Rqq[0]·HT = Rxx[0] (3) |
или более подробно
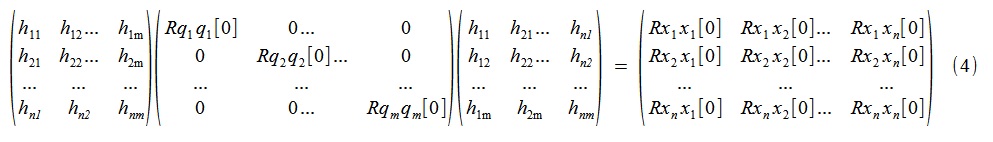
То есть поиск искомых таких «псевдособственных» форм колебаний и соответствующих им некоррелированных (при нулевом лаге) процессов q сводится к спектральному разложению (по собственным векторам и числам) симметричной матрицы Rxx[0] (составленной из значений авто- и взаимных корреляций процессов x при лаге Δτ= 0) Ее собственные ортонормированные вектора дают нам искомые формы, а действительные собственные значения — дисперсии соответствующих процессов (помимо значимых, скорее всего, будут дисперсии ~0, поэтому на практике обычно m
| q =HTx (5) |
Для пояснения изложенного рассмотрена модель линейной механической системы с пятью степенями свободы, приближенно имитирующей поведение струны в вязкой среде (рис. 2), 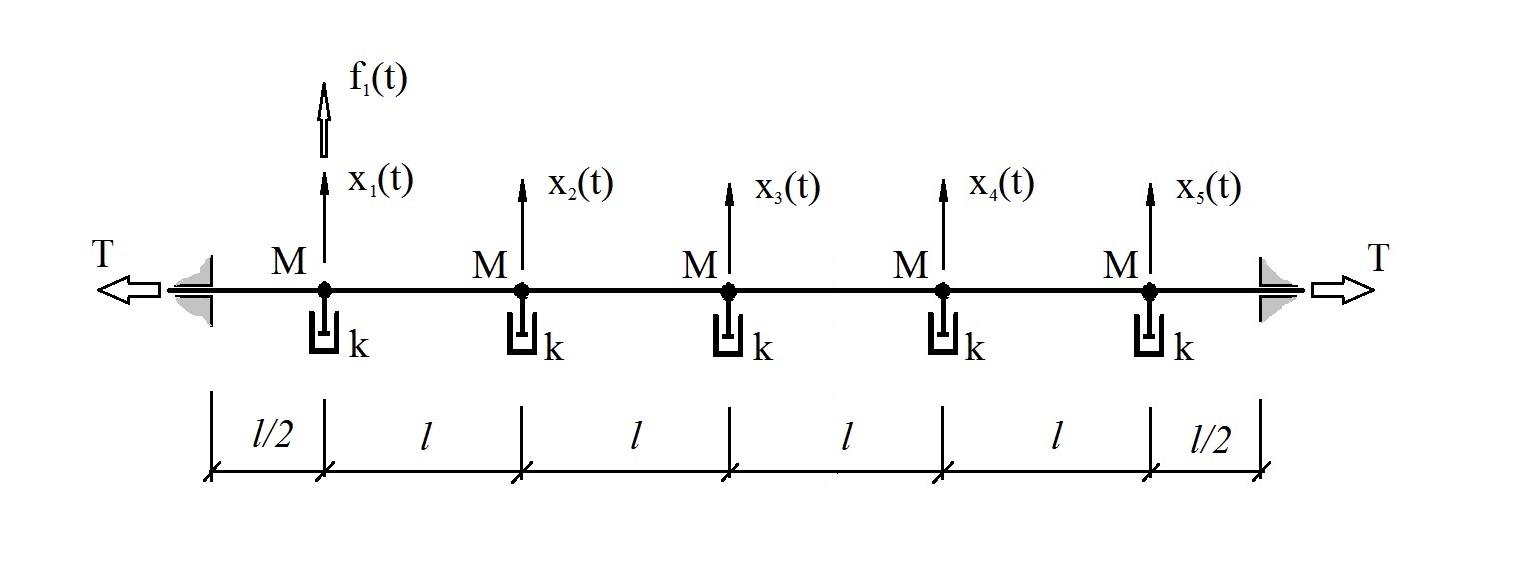
Рис. 2 Тестовая система.
колеблющейся под воздействием стохастического возмущения f1[i] типа розового шума (рис. 3), интервал дискретизации Δt=0,01с, длина реализации 25000 отсчетов.(Здесь и далее оценки СПМ получены методом Уэлча, длина сегмента 1024, применено окно Хэмминга и 60% перекрытие сегментов.) 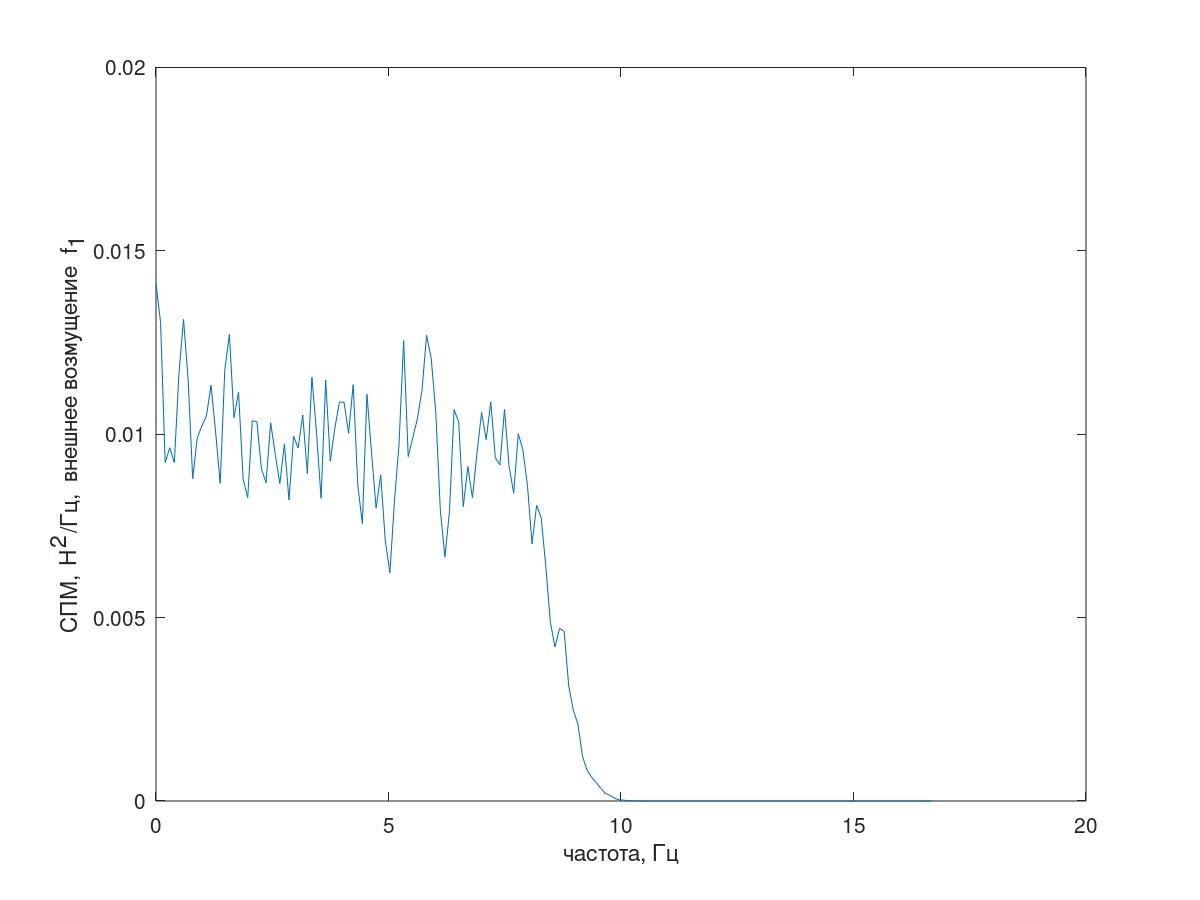
Рис. 3 Спектр внешнего возмущения.
Фрагмент временной реализации возмущения приведен на рис. 4.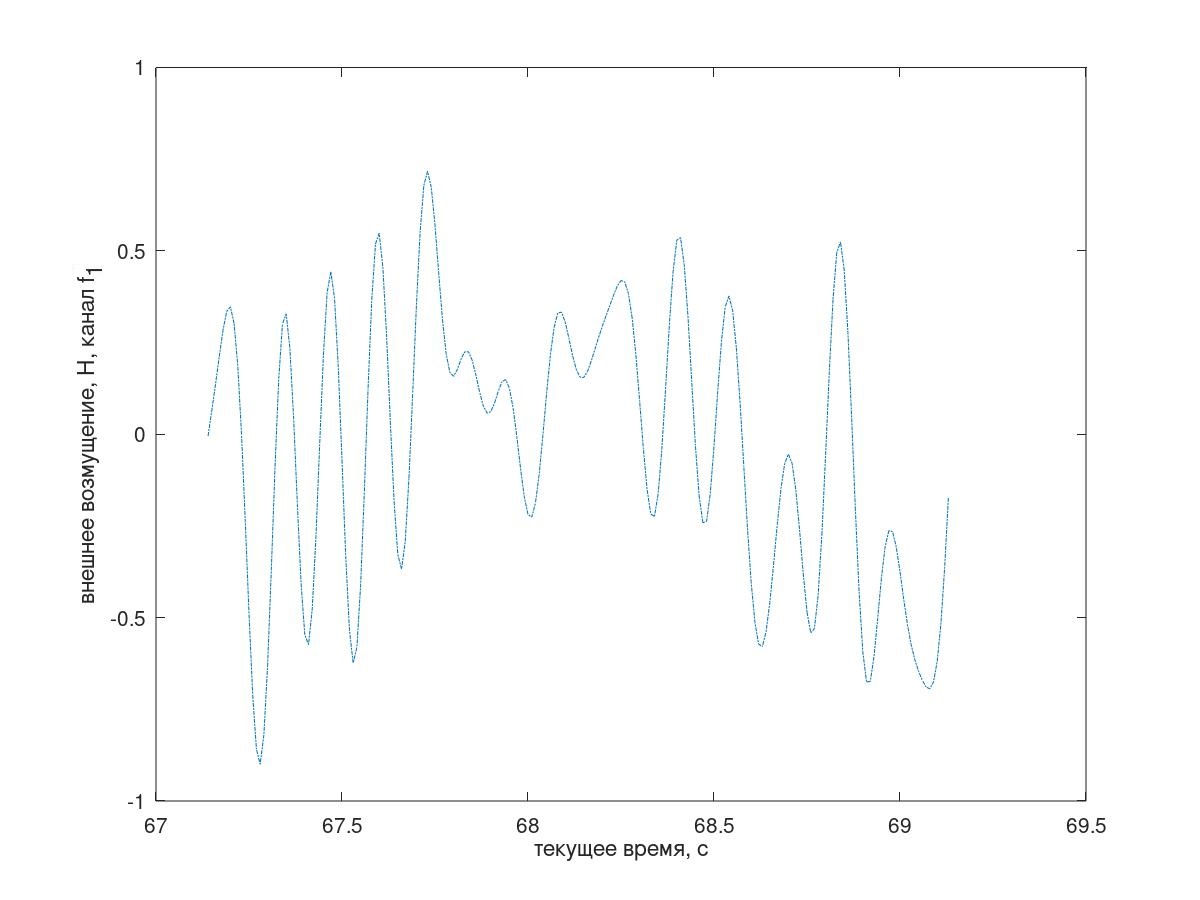
Рис. 4 Фрагмент временной реализации входящего возмущения
В непрерывном времени модель представляет собой систему диффуравнений (6), 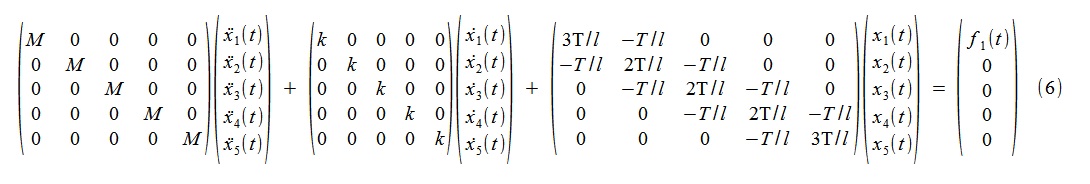
где M=1 кг, k= 10 кг/с, T=2000Н, l=1 м.
Соответствующие (понятно, какие) матрицы численно равны нижеприведенным:

Одна из АЧХ системы изображена на рис. 5.
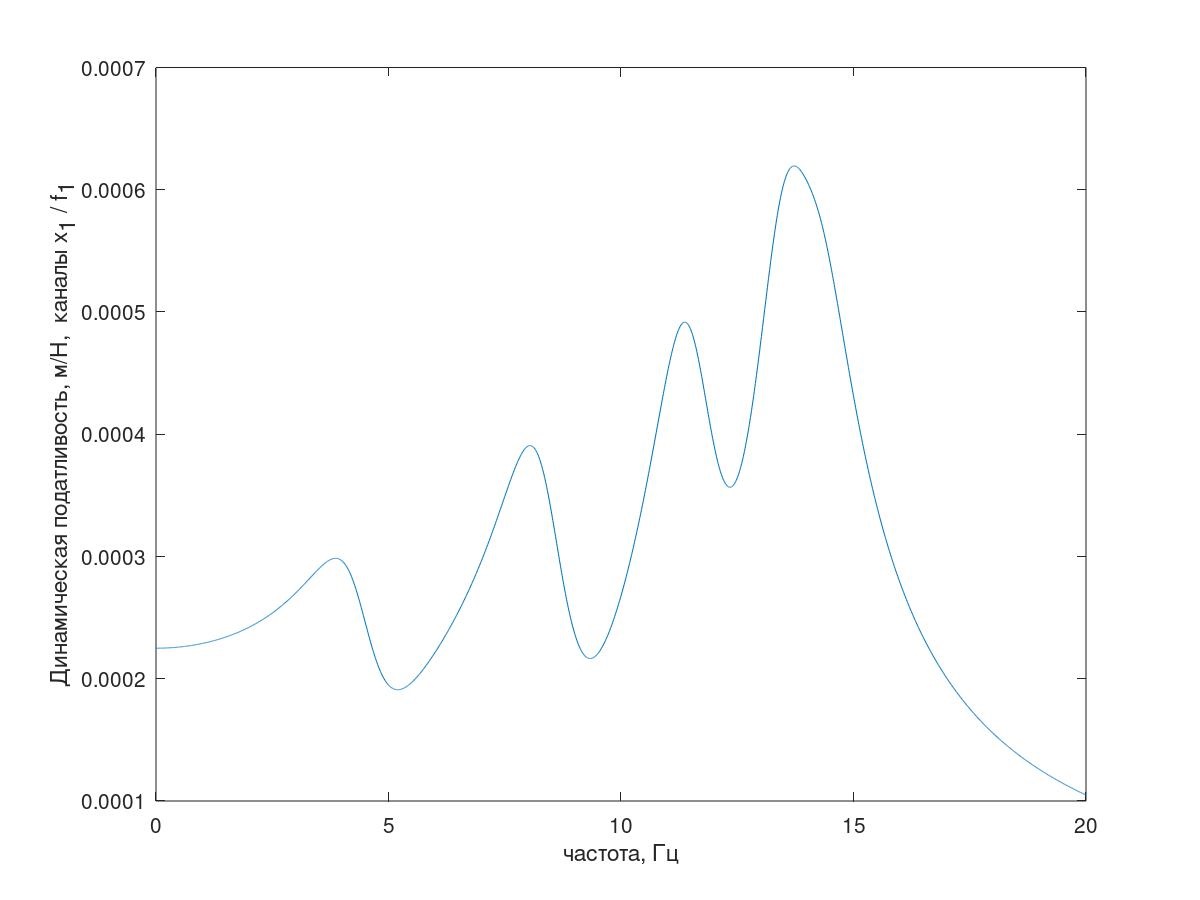
Рис. 5.АЧХ тестовой системы
(Пояснение — с количеством резонансных пиков там все в порядке, в качестве пояснения этого АЧХ системы с условно уменьшенным демпфированием (k=1 кг/с) приведена на рис. 5)
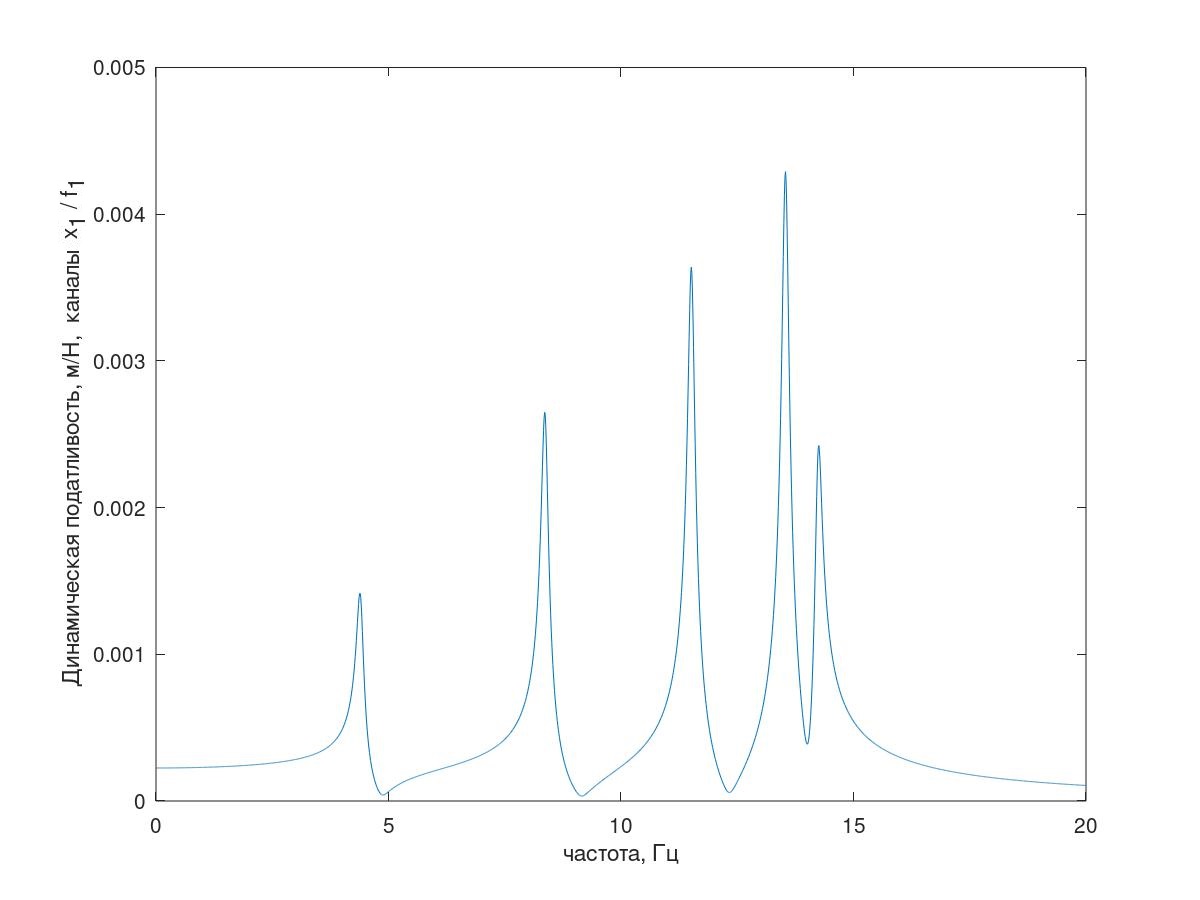
Рис. 6 Пояснение насчет пяти резонансов.
Для симуляционного моделирования в дискретном времени использована конечноразностная модель (КР-модели неплохо работают при малых интервалах дискретизации, как было показано). Полученный спектр отклика приведен на рис. 7. 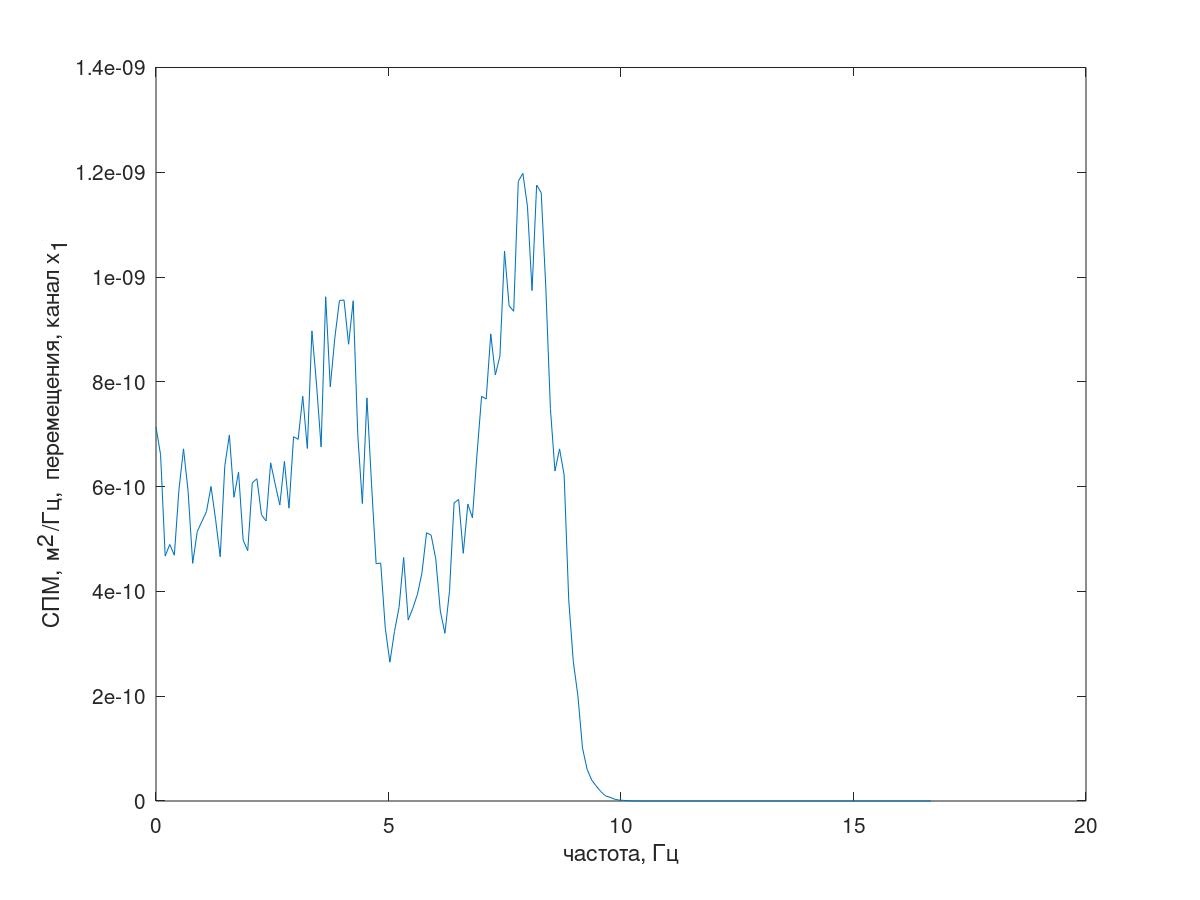
Рис. 7 Спектр отклика (канал x1)
Далее корелограммным методом были найдены значения авто- и взаимных корреляций каналов отклика.
Результаты применения обсуждаемого метода: найденны дисперсии псевдомодальных процессов Rqq и сами псевдособственные формы H: 
Количественно значимыми (по значениям их дисперсий в Rqq), по-видимому, являются три первых процесса в разложении, анимация всего многоканального процесса и соответствующих первых трех форм колебаний по 32 отсчетам (с 6714 по 6746 отсчет, т.е с 67,13с по 67,63с текущего времени) приведена на рис. 1 в начале статьи. Как можно заметить, данные псевдоформы имеют определенное сходство с собственными формами колебаний струны.
Накопленный опыт указывает на следующие особенности данного метода.
1. Метод чувствителен к посторонним шумам, в т.ч. высокочастотным. Существует опасность получения «случайных» результатов (с большой случайной ошибкой) и кажущейся невоспроизводимости экспериментальных результатов. Необходимо тщательно отфильтровывать нерабочую (количественно незначимую) часть частотного диапазона многоканального сигнала.
2. Лучшие результаты получены при количстве каналов наблюдения, существенно большем, чем количество ожидаемых проявляющихся форм колебаний (количество резонансных пиков в исследуемом диапазоне), т.е. при m<
4. По-видимому, сопоставляя истинные формы (найденные иными методами) и рассматриваемые псевдоформы, с некоторой вероятностью можно найти точки приложения внешнего возмущения (особенно при малоканальном возмущении), в случае, если такая задача актуальна.

