О линейной регрессии: байесовский подход к курсу05.04.2017 10:48

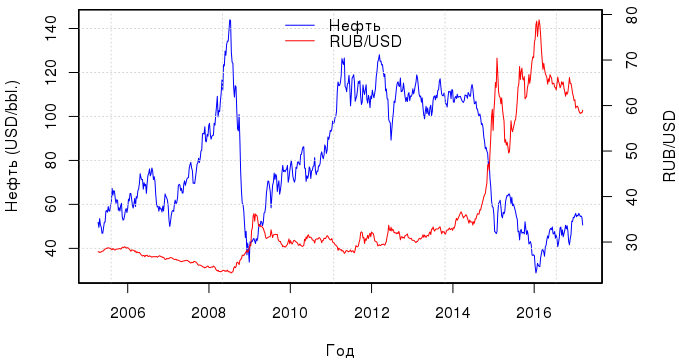
e100e15a9a3e42e4869217f10bc3132d.png
Не секрет, что курс рубля напрямую зависит от стоимости нефти (и от кое-чего еще). Этот факт позволяет строить довольно интересные модели. В своей статье о линейной регрессии я коснулся некоторых вопросов, посвященных диагностике модели, а за кадром остался такой вопрос: есть ли более эффективная, но не слишком сложная альтернатива линейной регрессии? Традиционно используемый метод наименьших квадратов прост и понятен, но есть и другие подходы (не такие понятные).


Данные и диагностика МНК


В этой статье мы сравним несколько линейных по своей сути моделей, используя в качестве наглядного пособия зависимость курса рубля от стоимости нефти. Помните этот замечательный пост? Спустя два года настало время обновить графики. Свежие данные загрузим с Quandl: за кодом «EIA/PET_RBRTE_D» скрывается спотовая цена на нефть марки Brent в $, а за «BOE/XUDLBK69» — стоимость 1 доллара в российских рублях.


Данные
library(Quandl)
library(zoo)
library(dplyr)
oil.ts <-Quandl("EIA/PET_RBRTE_D", trim_start="2005-04-03", trim_end="2017-03-10", type="zoo", collapse="weekly")
usd.ts <-Quandl("BOE/XUDLBK69", trim_start="2005-04-03", trim_end="2017-03-10", type="zoo", collapse="weekly")

Временной промежуток — с апреля 2005 по март 2017 года. И вот какая динамика наблюдается за этот период, если выразить стоимость рубля в долларах:
image
Если судить по графику, то связь между кривыми стоимости рубля и нефти прослеживалась постоянно, но после 2012 г. она стало особенно тесной. В принципе, нет особого смысла строить одну регрессию МНК за все эти года, т.к. в связи с резкими колебаниями цен остатки регрессии будут иметь мультимодальное распределение, и получится модель, которая все плохо описывает. Поэтому рассмотрим период с марта 2015 г. по декабрь 2016 г. — это будет обучающая выборка; данные за 2017 г. используем для тестирования.
Характер связи с 2015 г. не изменился, и линейная регрессия rubi=a+b·oili, построенная с помощью МНК статистически значима:


МНК
tr.s <- "2015-03-01"; tr.e <- "2016-12-31"
train <- data.frame(oil=as.vector(window(oil.ts, start=tr.s, end=tr.e)),
                    rub=as.vector(window(rub.ts, start=tr.s, end=tr.e)),
                    date=index(window(oil.ts, start=tr.s, end=tr.e))) %>% 
  mutate(month=factor(format(date, "%m")), 
         date=NULL)
te.s <- "2017-01-01"; te.e <- "2017-03-15"
test <- data.frame(oil=as.vector(window(oil.ts, start=te.s, end=te.e)),
                   rub=as.vector(window(rub.ts, start=te.s, end=te.e)),
                   date=index(window(oil.ts, start=te.s, end=te.e))) %>% 
  mutate(month=factor(format(date, "%m")), 
         date=NULL)
fit1 <- lm(rub ~ oil, data=train)
summary(fit1)
## 
## Call:
## lm(formula = rub ~ oil, data = train)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -2.096e-03 -3.265e-04  4.510e-06  3.491e-04  1.871e-03 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.284e-03  3.396e-04   21.45   <2e-16 ***
## oil         1.777e-04  7.009e-06   25.35   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0005883 on 94 degrees of freedom
## Multiple R-squared:  0.8724, Adjusted R-squared:  0.871 
## F-statistic: 642.7 on 1 and 94 DF,  p-value: < 2.2e-16

$rub_i=0.0073+0.000178\cdot oil_i$


Если убрать свободный член, то R2 будет почти равен единице. Этому есть объяснение. Как бы это ни было заманчиво, но просто так обнулять свободный член нельзя (разве что исследуемый процесс гарантирует, что линия регрессии проходит через начало координат): кому интересно, можно почитать здесь. Не стоит зацикливаться на R2 — этот критерий достаточно формален. Что касается остатков модели, то они распределены в целом неплохо, но, похоже, бимодально: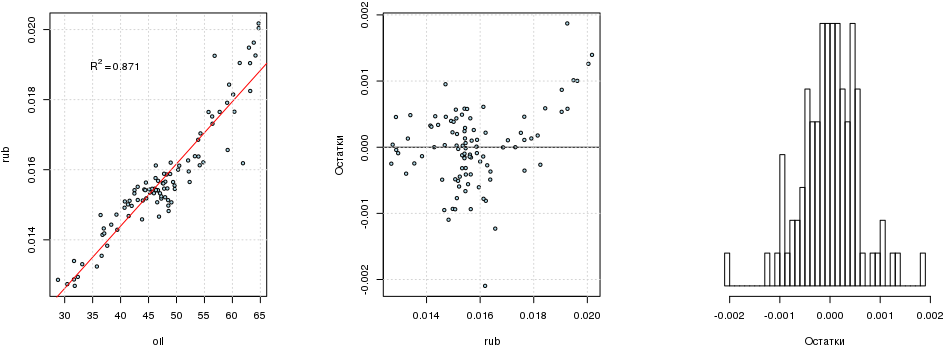
остатки


Диагностика модели
library(lmtest)
dwtest(fit1)
## 
##  Durbin-Watson test
## 
## data:  fit1
## DW = 0.49421, p-value < 2.2e-16
## alternative hypothesis: true autocorrelation is greater than 0
resettest(fit1)
## 
##  RESET test
## 
## data:  fit1
## RESET = 13.999, df1 = 2, df2 = 92, p-value = 4.924e-06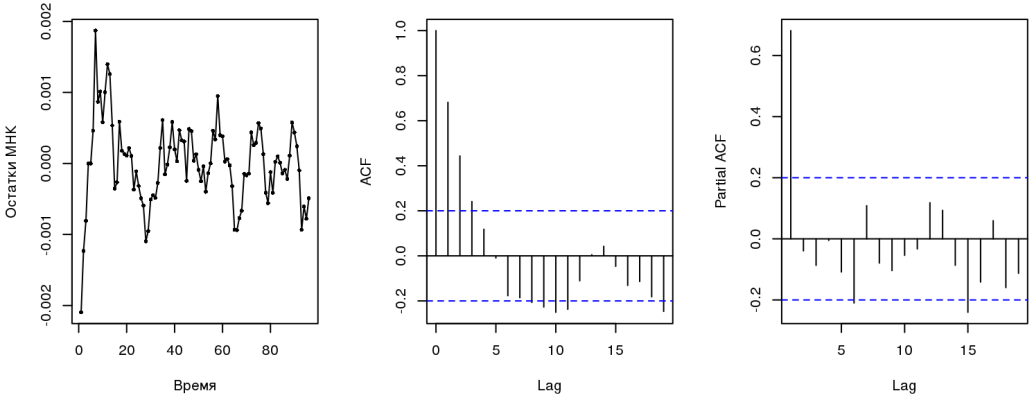

image
Тест Дарбина-Уотсона говорит о наличии (кто бы мог подумать) автокорреляции; коррелограммы остатков указывают на процесс типа AR (1) (об этом мы поговорим ниже). RESET-тест свидетельствует о пропущенных переменных, что логично, т.к. на курс влияет множество факторов (либо МНК — не самая подходящая модель). Все это вместе нарушает предпосылки, которые лежат в основе МНК. Тот, кто занимается эконометрикой, скажет, что пользоваться такой регрессией надо осторожно, т.к. все оценки смещенные и несостоятельные, нельзя строить доверительные интервалы. Из всех свойств сохраняется только линейность.


Можно провернуть еще такой трюк: возможно, зависимость не линейная, а включает и полиномиальные члены. Как выбрать более-менее оптимальную модель? Придется воспользоваться либо перекрестной проверкой, либо информационным критерием типа AIC. Для линейной модели последний мне больше нравится, тем более, что в асимптотике результаты AIC и CV сходятся. Код, приведенный ниже, как раз выполняет то, что нужно: строятся полиномиальные регрессии со степенью от 1 до 5, и на основании минимума критерия AIC определяется оптимальная модель. Функция poly () строит ортогональные полиномы, и именно их надо использовать при регрессии.


which.min(sapply(1:5, function(i) AIC(lm(rub ~ poly(oil, i), data=train))))
## [1] 3

Таким образом, получается, что модель может иметь и такой вид:


$rub_i=a+b\cdot oil_i + b_2\cdot oil_i^2 + b_3\cdot oil_i^3$


Временные ряды и ошибки


О временных рядах можно рассуждать бесконечно и с переменным успехом. Нам же надо знать вот что. И курс рубля, и стоимость нефти являются временными рядами, и не учитывать это нельзя (отсюда и возникают проблемы с ошибками в МНК). Некоторые же процессы можно описать с помощью простой авторегрессионной модели первого порядка. Это означает, что следующее значение во временном ряду хорошо описывается предыдущим плюс небольшая ошибка:


$u_{t}=c+\phi u_{t-1}+\epsilon_t,$


где εt — белый шум.
Построим модель ARIMA с дополнительным регрессором:


ARIMA
library(forecast)
fit2 <- auto.arima(train$rub, xreg=train$oil)
summary(fit2)
## Series: train$rub 
## Regression with ARIMA(1,0,0) errors 
## 
## Coefficients:
##          ar1  intercept  train$oil
##       0.9123     0.0108      1e-04
## s.e.  0.0417     0.0004      0e+00
## 
## sigma^2 estimated as 1.274e-07:  log likelihood=626.46
## AIC=-1244.91   AICc=-1244.47   BIC=-1234.65
## 
## Training set error measures:
##                        ME        RMSE          MAE        MPE     MAPE
## Training set 1.424521e-05 0.000351317 0.0002580076 0.02303551 1.610766
##                   MASE       ACF1
## Training set 0.7766594 0.02983604

Из информации об этой модели можно узнать, что при регрессии rubi=a+b·oili + ui ошибки ui имеют автокорреляционную структуру ARIMA (1, 0, 0), т.е. как раз и представляют собой авторегрессионную модель первого порядка AR (1).


Т.к. теперь структура ошибок приблизительно известна, попробуем обобщенный метод наименьших квадратов (GLS). В GLS используется простая идея, которая заключается в следующем. Если при решении системы y=Xb+ε методом наименьших квадратов коэффициенты при регрессорах и ковариационная матрица находятся из уравнений


$ b_{OLS}=(X^TX)^{-1}X^Ty \\ Var(b_{OLS})=\sigma^2(X^TX)^{-1}, $


то при использовании GLS соответствующие уравнения будут иметь такой вид:


$ b_{GLS}=(X^T\Sigma^{-1}X)^{-1}X^T\Sigma^{-1}y \\ Var(b_{GLS})=(X^T\Sigma^{-1}X)^{-1} $


Тут Σ — ковариационная матрица ошибок, которую можно оценить, зная их структуру. В теории такая модель дает несмещенные, эффективные, состоятельные и асимптотически нормальные оценки (теорема Айткена).


GLS
library(nlme)
fit3 <- gls(rub ~ oil, data=train, correlation=corAR1(value=0.7, form=~1|month))
summary(fit3)
## Generalized least squares fit by REML
##   Model: rub ~ oil 
##   Data: train 
##         AIC       BIC   logLik
##   -1173.847 -1163.674 590.9237
## 
## Correlation Structure: AR(1)
##  Formula: ~1 | month 
##  Parameter estimate(s):
##       Phi 
## 0.7478772 
## 
## Coefficients:
##                   Value    Std.Error  t-value p-value
## (Intercept) 0.007860934 0.0004055443 19.38366       0
## oil         0.000163683 0.0000081087 20.18601       0
## 
##  Correlation: 
##     (Intr)
## oil -0.952
## 
## Standardized residuals:
##         Min          Q1         Med          Q3         Max 
## -2.96100735 -0.41075284  0.07903953  0.62870157  3.42607023 
## 
## Residual standard error: 0.0006099571 
## Degrees of freedom: 96 total; 94 residual

$rub_i=0.00786+0.000164\cdot oil_i$


Можно еще проверить, получим ли мы какую-либо выгоду от включения полиномиальных членов в GLS согласно критерию AIC: 


which.min(sapply(1:5, function(i) {
  d <- data.frame(poly(train$oil, i), month=train$month, rub=train$rub)
  AIC(gls(rub ~ . - month, data=d, correlation=corAR1(value=0.7, form=~1|month)))
}))
## [1] 1

Теперь достаточно регрессора в 1 степени. И, кстати, сами скорректированные ошибки модели распределены интереснее (хотя нельзя не отметить наличие выбросов):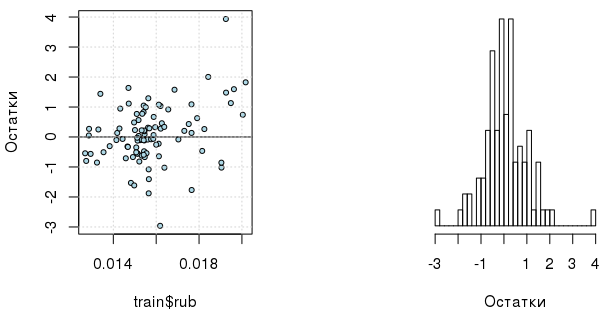
im


Регрессия Байеса и вероятностный выбор переменных


К этому моменту у нас есть три модели: OLS, ARIMA (1, 0, 0), GLS с ошибками AR (1). Теперь рассмотрим задачу с другой стороны и в иной постановке, задаваясь прежде всего вопросом, нужны ли нам, например, полиномиальные члены:


$ y_i \sim N(a + X_i^T \cdot b, \tau) \\ X_i = [x_i, x_i^2, x_i^3, x_i^4, x_i^5 ] \\ b = [b_1, b_2, b_3, b_4, b_5]\\ b_j = I_j \cdot b_{{\tau}_j},\ j=1..5 \\ I_j \sim Bernoulli(p) \\ b_{\tau_j} \sim N(0, \tau_b) \\ a \sim N(0, 10^{-4}) \\ \tau \sim Gamma(1, 10^{-3}) \\ \tau_b \sim Gamma(1, 10^{-3}) \\ p \sim Beta(2, 9) $


Тут записано, что переменная yi распределена нормально и линейно зависит от степеней xi. В свою очередь коэффициенты регрессии не просто распределены нормально, но и еще могут «отсутствовать» в уравнении, что обеспечивается идикаторной переменной Ij, которая подчиняется распределению Бернулли с параметром p, т.е. может принимать только значения 0 или 1. Параметр p в свою очередь берется из бета-распределения, а параметры τ и τb — из гамма. Так мы задали априорные распределения. Откуда известны их точные формы? Вот здесь теория не очень внятная и предлагает опираться либо на наши практические понятия о природе описываемых процессов или интуицию, либо задавать неинформативные априорные распределения. К счастью, чем больше данных доступно, тем меньше вывод зависит от априорных распределений. И это становится понятным, если взглянуть на формулу Байеса, которая представляет собой правило, согласно которому изменяются априорные распределения при наблюдении определенных данных:


$ p(\theta| y) = \frac{p(y|\theta)}{p(y)}p(\theta)\propto p(y|\theta)p(\theta) $


Тут p (θ|y) — апостериорное распределение, p (y|θ) — правдоподобие, p (θ) — априорное распределение. Тогда можно записать:


$p(\theta|y_1) \propto p(y_1|\theta)p(\theta)$


И далее по инерции:


$p(\theta|y_1,\ldots,y_i) \propto p(y_i|\theta)p(\theta|y_1,\ldots,y_{i-1})$


Но все же желательно, чтобы распределения были более-менее осмысленными. Так, если посмотреть на гистограмму yi (у нас это курс рубля), то там можно увидеть кривую, напоминающую нормальное распределение (или логнормальное…). А что касается коэффициентов регрессии, то здесь выбор распределения Гаусса оправдан традиционным ожиданием того, что они распределены нормально.


Конечно, никто не хочет заниматься увлекательным выводом вручную, поэтому нам понадобится библиотека, позволяющая описывать модель в терминах априорных распределений. В R это rjags, и еще функции-обертки из R2jags. Все вышеизложенное запишется в таком виде:


Bayesian Variable Selection
library(R2jags)
model1 <- "model {
  for (i in 1:n) {
    y[i] ~ dnorm(a + inprod(X[i,], b[]), tau)
  }
  for (j in 1:p) {
    ind[j] ~ dbern(pind)
    bT[j] ~ dnorm(0, taub)
    b[j] <- ind[j] * bT[j]
  }
  a ~ dnorm(0, 1e-04)
  tau ~ dgamma(1, 1e-03)
  taub ~ dgamma(1, 1e-03)
  pind ~ dbeta(2, 9)
}"
p <- 5
m.jags1 <- jags(data=list(y=train$rub,
                          X=poly(train$oil, p),
                          n=nrow(train),
                          p=p),
                parameters.to.save=c("a", "b", "ind"),
                model.file=textConnection(model1),
                n.chains=1, n.iter=5000)
m.jags1
## Inference for Bugs model at "5", fit using jags,
##  1 chains, each with 5000 iterations (first 2500 discarded), n.thin = 2
##  n.sims = 1250 iterations saved
##           mu.vect sd.vect     2.5%      25%      50%      75%    97.5%
## a           0.016   0.000    0.015    0.015    0.016    0.016    0.017
## b[1]        0.011   0.007    0.000    0.006    0.013    0.017    0.023
## b[2]        0.000   0.001    0.000    0.000    0.000    0.000    0.003
## b[3]        0.000   0.001    0.000    0.000    0.000    0.000    0.000
## b[4]        0.000   0.001    0.000    0.000    0.000    0.000    0.000
## b[5]        0.000   0.001    0.000    0.000    0.000    0.000    0.000
## ind[1]      0.764   0.425    0.000    1.000    1.000    1.000    1.000
## ind[2]      0.046   0.210    0.000    0.000    0.000    0.000    1.000
## ind[3]      0.034   0.180    0.000    0.000    0.000    0.000    1.000
## ind[4]      0.031   0.174    0.000    0.000    0.000    0.000    1.000
## ind[5]      0.045   0.207    0.000    0.000    0.000    0.000    1.000
## deviance -848.261  15.731 -876.531 -858.633 -848.740 -838.639 -815.570
## 
## DIC info (using the rule, pD = var(deviance)/2)
## pD = 123.7 and DIC = -724.5
## DIC is an estimate of expected predictive error (lower deviance is better).

Вывод показывает, что средние значения индикаторных переменных Ij при коэффициентах регрессии b2,…, b5 на порядок меньше I1, а это значит, что такая вероятностная модель дает нам право предположить, что курс рубля линейно зависит от стоимости нефти. Далее запишем простую линейную модель, учитывающую наличие авторегрессии первого порядка в ошибках:


Bayes AR1
model2 <- "model {
  a ~ dt(0, 5, 1)
  b ~ dt(0, 5, 1)
  phi ~ dunif(-1, 0.999)
  tau0 ~ dgamma(1, 1e-03)
  tau[1] <- tau0
  y[1] ~ dnorm(a + b * x[1], tau[1])
  for (i in 2:n){
    tau[i] <- tau0 + phi * tau[i-1]
    y[i] ~ dnorm(a + b * x[i], tau[i])

  }
}"
set.seed(123)
n <- nrow(test)
m.jags2 <- jags(data=list(y=c(train$rub, rep(NA, n)),
                          x=c(train$oil, test$oil),
                          n=nrow(train)+n),
                parameters.to.save=c("a", "b", "phi", "y"),
                model.file=textConnection(model2),
                n.chains=1, n.iter=5000)

Так выглядят апостериорные распределения параметров модели: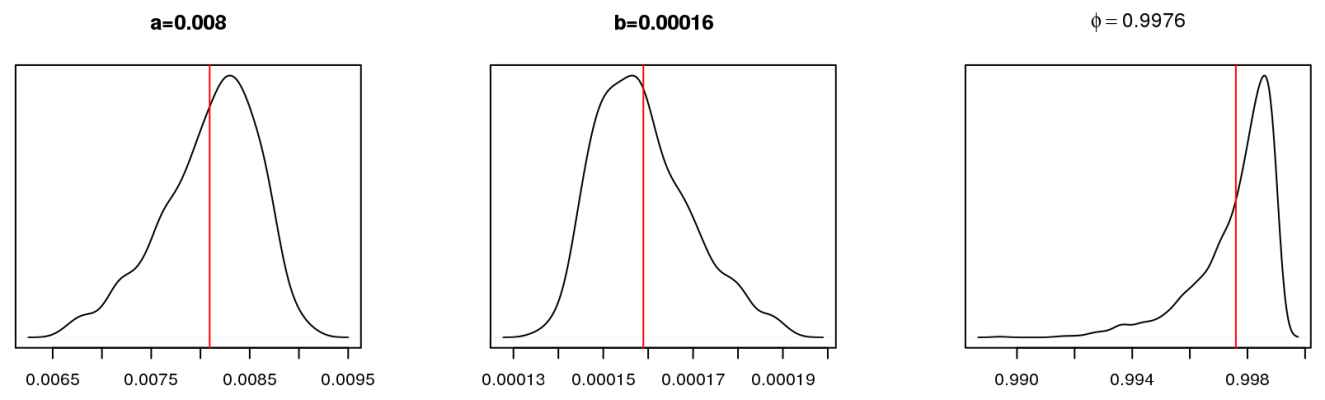
image
Можно заметить, что они не сильно отличаются от параметров модели GLS. Само уравнение регрессии для средних значений параметров можно записать так:


$ rub_i \sim N(0.0081+0.000157\cdot oil_i, \tau_i) $


А вот 95% вероятностные интервалы в привычном виде для предсказанных значений курса доллара в 2017 г. (красными треугольниками показаны истинные значения):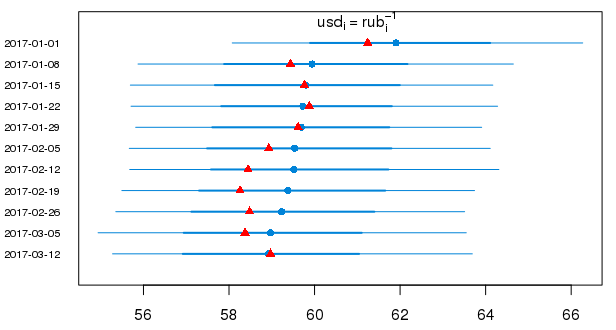
image


Заключение


Ниже показан график с предсказаниями курса доллара моделями и их ошибки. Такими вот нехитрыми манипуляциями мы добились уменьшения MAE с 3.1e-04 у OLS до 2.7e-04 при использовании байесовского подхода с учетом авторегрессионного процесса в ошибках модели, причем GLS показал примерно такой же результат, как и байесовский подход, но с меньшими моральными затратами.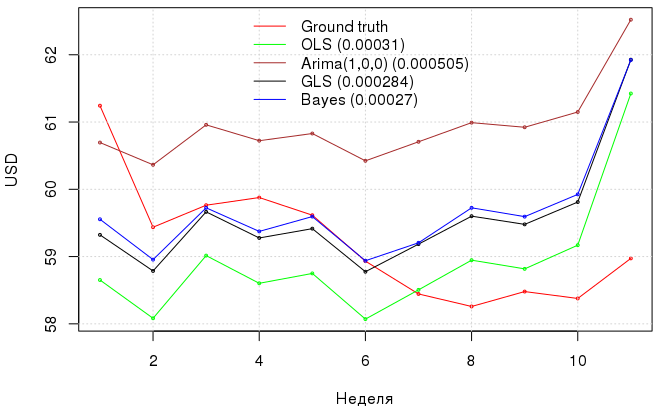
image
Зачем вообще было обращаться к такому выводу, если в итоге мы все равно получили модель, которая не слишком уж и превзошла OLS? Во-первых, теперь формально мы не нарушаем предпосылки к МНК; во-вторых, получили вероятностное подтверждение, что модель все же не включает полиномиальные члены; в-третьих, теперь можно получать вероятностный (а не доверительный!) интервал для интересующей нас величины. Например, если нас интересует, сколько будет стоить доллар в рублях с вероятностью в 95% при стоимости нефти 50.63USD/bbl., то можно получить вот такое распределение: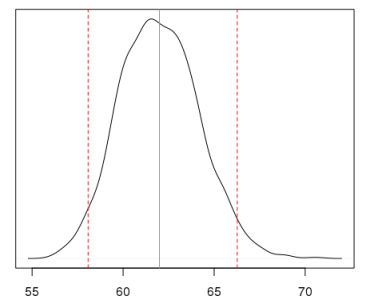
image
Конечно, такая регрессия с применением вероятностного вывода требует определенных усилий и некоторого опыта. С другой стороны, если надо что-то быстро посчитать, неохота возиться с распределенями, вероятностные интервалы неинтересны, а ошибки модели коррелированы, то стоит обратить внимание на незаслуженно редко используемый обобщенный метод наименьших квадратов (GLS), который позволяет получать более надежные оценки, чем при слепом использовании OLS. Кроме того, не стоит забывать об auto.arima (), которая позволяет быстро оценить корреляционный процесс в остатках модели.


Bonus


Есть еще интересная и вполне очевидная корреляция — между курсом рубля и международными резервами: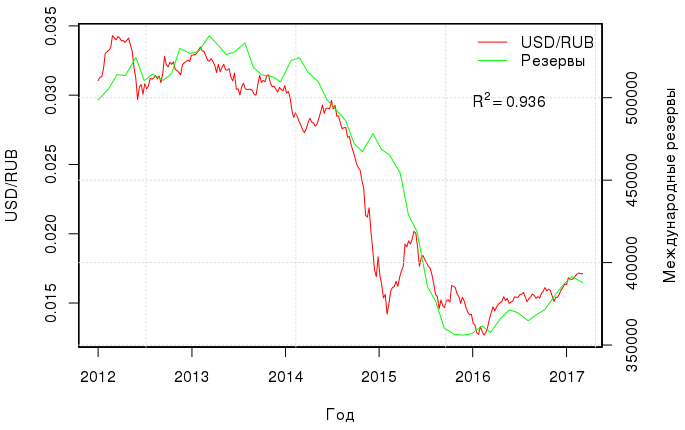
image
Если построить линейную регрессию между этими двумя величинами, то коэффициент детерминации будет равен аж 0.936. Модель с двумя регрессорами (нефть и резервы) имеет R2=0.98, и, что самое приятное, RESET-тест Рамсея подтверждает, что в этой регрессии нет пропущенных переменных, т.е. курс рубля вполне себе объясняется стоимостью нефти и международными резервами:


$ rub_i=-8.713 \cdot 10^{-3}+1.458 \cdot 10^{-4} \cdot oil_i +4.648 \cdot 10^{-8} \cdot res_i, $


или, если отмасштабировать переменные:


$ rub_i=0.0254+0.0042 \cdot oil_i +0.0031 \cdot res_i, $

Комментарии (2)

  • 5 апреля 2017 в 10:40

    0

    ↑

    ↓

    Отличная работа, спасибо, очень интересно.

    • 5 апреля 2017 в 10:43

      0

      ↑

      ↓

      Спасибо. Думаю, часть про международные резервы надо будет подробнее рассмотреть.

© Habrahabr.ru