О форме вращающейся жидкости03.01.2018 12:03

Сегодня я заварил себе чай и задумался

Сегодня утром я задумался, пока размешивал два кубика сахара в чашке с только что заваренным чаем. Задумался о форме жидкости, которую она принимает при вращении. Безусловно, все представляют себе что будет, если очень быстро начать размешивать сахар в чашке с чаем. Мне захотелось рассмотреть этот банальный и привычный процесс подробнее и попытаться рассказать Вам немного интересного из физики окружающих нас в быту явлений.

Идея эксперимента

Давайте представим, что мы имеем некоторую цилиндрическую тару, в которой находится некоторая жидкость. Вращаться жидкость можно заставить, как минимум, двумя очевидными способами: размешать её каким-нибудь предметом или начать вращать цилиндрическую тару, что, благодаря силам трения между жидкость и поверхностью сосуда, приведет к вращению жидкости, увлекаемой содержащим её вращающимся сосудам.

Физическая модель

Остановимся на втором варианте. Итак, у нас есть вращающийся с постоянной циклической частотой сосуд, в котором при динамическом равновесии с постоянной циклической частотой вращается жидкость в том же направлении.

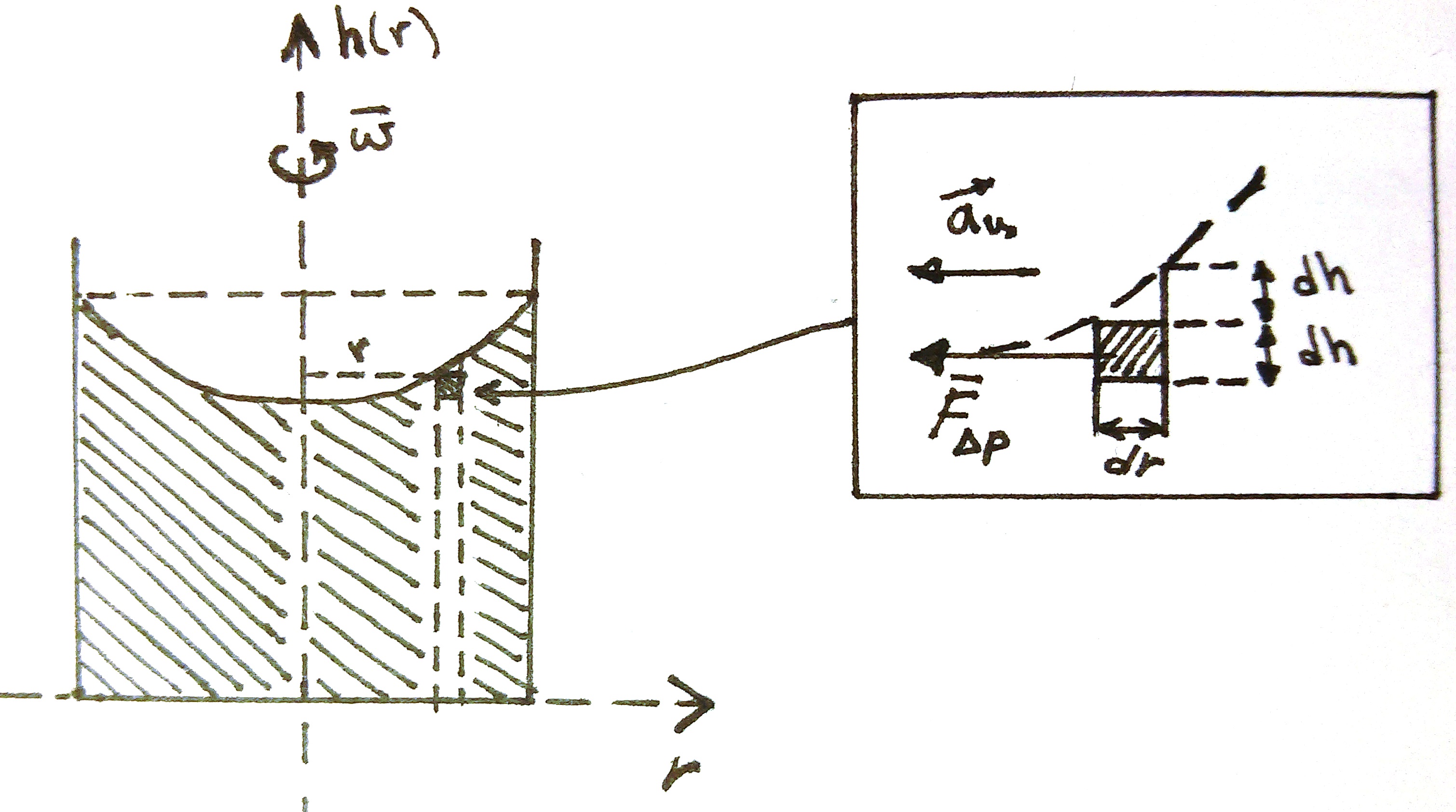
Вырежем из всей жидкости элементарный бесконечно малый объем около поверхности и рассмотрим какие силы на него действуют. В силу симметрии задачи, будем ориентироваться на цилиндрические координаты, что заметно упростит расчеты.

Качественный расчет формы поверхности

Запишем второй закон Ньютона для элементарного кусочка объема жидкости:
$m\overrightarrow a = \sum\limits_i {\overrightarrow F _i }$
К примеру, после размешивания ложкой сахара в чашке только что заваренного чая, жидкость вращается вокруг оси симметрии, отсюда наш элементарный кусочек объема имеет центростремительное ускорение. Поэтому спроецируем наш закон Ньютона на ось, совпадающую с радиусом-вектором от элементарного объема до оси симметрии. Не будем учитывать вязкость и поверхностное натяжение. Сила, сообщающая центростремительное ускорение (в правой части нашего закона движения) возникнет из-за разности давлений столбов жидкости, что можно увидеть на увеличенной части первого рисунка.

Таким образом, у нас получится следующее выражение:
$Or:ma_{c} = F_{\Delta p}$ , где $a_{c} = \frac{{v^2 }}{r} = \frac{{\left( {\omega r} \right)^2 }}{r} = \omega ^2 r$ , а та самая сила определится как $F_{\Delta p} = \Delta p \cdot S_{eff.section}$ , где площадью эффективного сечения $S_{eff.section} = rd\varphi \cdot dh = rd\varphi dh$ обозначена та площадь нашего элементарного объема, на которую действует разница давлений столбов жидкости $\Delta p = \rho gdh$ .
Получаем силу $F_{\Delta p} = \rho gdh \cdot rd\varphi dh = \rho grd\varphi \left( {dh} \right)^2$

Масса нашего элемента объема определяется по знакомой всем формуле $m = \rho dV$ , а сам объем будет равен $dV = rd\varphi \cdot dh \cdot dr$ (элементарный объем в цилиндрических координатах).
В итоге, 2 закон Ньютона для нашей маленькой задачки расписывается в следующее выражение:
$\rho rd\varphi \cdot dh \cdot dr \cdot \omega ^2 r = \rho grd\varphi \left( {dh} \right)^2$
После небольших сокращений и преобразований получаем:
$\omega ^2 rdr = gdh$
Теперь проинтегрируем обе части выражения, используя неопределенные интегралы:
$\int {\omega ^2 rdr = \int {gdh} }$
$\omega ^2 \frac{{r^2 }}{2} = gh + const$
$h(r) = \frac{{\omega^2 }}{{2g}}r^2 + C$

Детальный расчет формы поверхности

Теперь мы получили вполне ясную зависимость для формы поверхности и с уверенностью можем сказать, что это параболоид. Но нам неизвестна постоянная величина $C$ . Давайте её определим для полного понимания физики процесса.

Так как объем жидкости не меняется (мы считаем, что не пролили ни капли, пока размешивали наш чай ツ), то запишем объемы до вращения и во время вращения с постоянной циклической частотой.

До вращения:
$V = \pi R^2 H$ , где $H$ — это высота жидкости в цилиндрической поверхности в спокойном состоянии (вращения нет).

Во время вращения:
$V = \int {\int {\int {dV} } } = \int {\int {\int {rd\varphi dhdr} } }$
$\begin{array}{l} V = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {rdr} \int\limits_0^{\frac{{\omega ^2 }}{{2g}}r^2 + C} {dh} = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {r\left( {\frac{{\omega ^2 }}{{2g}}r^2 + C} \right)dr} = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {\left( {\frac{{\omega ^2 }}{{2g}}r^3 + Cr} \right)dr} = \\ = \int\limits_0^{2\pi } {\left( {\frac{{\omega ^2 }}{{8g}}R^4 + \frac{C}{2}R^2 } \right)d\varphi } = \left( {\frac{{\omega ^2 }}{{8g}}R^4 + \frac{C}{2}R^2 } \right)2\pi = \frac{{\pi \omega ^2 }}{{4g}}R^4 + \pi CR^2 \\ \end{array}$

Данные объемы равны, поэтому:
$\pi R^2 H = \frac{{\pi \omega ^2 }}{{4g}}R^4 + \pi CR^2$
Отсюда выражается ранее неизвестная постоянная: $C = \frac{1}{{R^2 }}\left[ {R^2 H - \frac{{\omega ^2 }}{{4g}}R^4 } \right] = H - \frac{{\omega ^2 }}{{4g}}R^2$
И окончательное уравнение формы поверхности вращающейся жидкости имеет вид:
$h(r) = \frac{{\omega ^2 }}{{2g}}r^2 + H - \frac{{\omega ^2 }}{{4g}}R^2$ или преобразовав $h(r) = \frac{{\omega ^2 }}{{2g}}\left( {r^2 - \frac{{R^2 }}{2}} \right) + H$

Некоторые заметки

Хотелось бы обратить внимание на то, что форма поверхности зависит от частоты вращения, ускорения свободного падения, геометрических параметров сосуда, первоначального объема жидкости, но не зависит от плотности жидкости. Это выражение мне показалось довольно интересным, так как с его помощью можно легко смоделировать примерное расположение жидкости внутри вращающегося вокруг своей оси симметрии цилиндрического сосуда. Для этого можно воспользоваться MathCAD«ом и построить несколько графиков.

Графическое представление результатов расчета

Возьмем вполне реальные параметры системы, соизмеримые с размерами чашки или стакана.
Радиус цилиндрической поверхности: $R0: = 0.05$
Высота жидкости в цилиндрической поверхности без вращения: $H0: = 0.1$
Ускорение свободного падения: $g0: = 9.81$
Циклическая частота вращения цилиндрической поверхности: $w0$
(Все значения этих величин заданы в системе Си)

Далее перепишем нашу функцию для её отображения в MathCAD.
Для 2D отображения сечения:
$h(r): = if\left( { - R0 \le r \le R0,\frac{{w0^2 }}{{2 \cdot g0}} \cdot \left( {r^2 - \frac{{R0^2 }}{2}} \right) + H0,0} \right)$

Для 3D отображения поверхности:
$N0: = 100$
$i: = 0..N0$
$j: = 0..N0$
$x_i : = 0.001 \cdot \left( {2 \cdot i - N0} \right)$
$y_j : = 0.001 \cdot \left( {2 \cdot j - N0} \right)$
$r(x,y): = \sqrt {x^2 + y^2 }$
$hv(x,y): = \frac{{w0^2 }}{{2 \cdot g0}} \cdot \left( {r^2 (x,y) - \frac{{R0^2 }}{2}} \right) + H0$
$fh(x,y): = if\left( { - R0 \le r(x,y) \le R0,if(hv(x,y) \ge 0,hv(x,y),0),0} \right)$
$M_{i,j} : = fh(x_i ,y_j )$

В качестве изменяющегося параметра будем менять циклическую частоту вращения $w0$ . Результаты можно наблюдать на рисунках ниже:

При циклической частоте $w0 = 0(рад/c)$

При циклической частоте $w0 = 5(рад/c)$

При циклической частоте $w0 = 15(рад/c)$

При циклической частоте $w0 = 25(рад/c)$

При циклической частоте $w0 = 39.5(рад/c)$

При циклической частоте $w0 = 90(рад/c)$

Выводы

Видно, что если циклическая частота превысит значение $w0 = 39.5(рад/c)$ , то мы увидим дно вращающегося цилиндрического сосуда, и, начиная с этой частоты, жидкость будет плавно «переходить» на стенки сосуда, всё сильнее оголяя дно. Очевидно, что при очень больших частотах вся жидкость растечется по стенкам сосуда. Теперь мы знаем все параметры такой жидкости. Зная её уравнение, не составит большого труда рассчитать толщину слоя жидкости на стенке сосуда на определенной высоте при определенной частоте.