Нумерология: никакого гадания, только теория чисел10.05.2021 17:17

В данной статье речь пойдёт о таких понятиях теории чисел, как цифровой корень и ведический квадрат.

Данная статья ничего не говорит о нумерологии, кроме того, что это псевдонаучная концепция.

Цель данной статьи: показать математические закономерности вокруг вычисления цифрового корня и его связь с циклическими числами.

Введение

Несколько дней назад я решил написать незатейливую статью про нумерологическое сложение. Моей целью было показать, что даже такая незамысловатая операция может иметь большое количество интересных закономерностей. Многие из этих закономерностей я нашёл ещё в школьное время, когда скучал на уроках географии. При внимательном рассмотрении я нашёл больше закономерностей, чем ожидал, и это привело меня назад к моей любимой теме full reptend prime.

После я внимательно изучил то, что нашёл, узнал, что многие из этих понятий уже существуют, и решил переписать статью заново, чтобы опираться на общеизвестные понятия. Помимо известных понятий я добавил собственные визуализации, чтобы сделать чтение немного более увлекательным.

Сумма цифр и цифровой корень

Цифровой корень натурального числа в заданной системе счисления — это значение, получаемое итеративным расчётом суммы цифр, где на первой итерации происходит расчёт суммы цифр натурального числа, а на каждой следующей — расчёт суммы цифр результата предыдущей итерации. Операция выполняется до тех пор, пока вычисленное значение не становится меньше заданной системы счисления, т.е. до тех пор, пока оно не равняется одной-единственной цифре.

Аддитивная стойкость натурального числа — это количество итераций, на которых нужно применить операцию суммы цифр, для того чтобы получить цифровой корень.

Пример: Цифровая сумма числа 142857 равна 1 + 4 + 2 + 8 + 5 + 7 = 27

Цифровая сумма числа 27 равна 2 + 7 = 9

Как следствие, цифровой корень числа 142857 = 9, аддитивная стойкость 142857 = 2.

Код для вычисления цифрового корня в произвольной системе счисления на языке Python:

def digitalRootRecurrent(number, base):
    digitSum = 0
    while number > 0:
        digitSum += number % base 
        number //= base
    if digitSum >= base:
        digitSum = digitalRootRecurrent(digitSum, base)
    return digitSum

Применение цифровой суммы

Цифровые суммы применялись при расчёте контрольных сумм для проверки арифметических операций ранних компьютеров. Ранее, в эпоху ручного счета, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из математических таблиц логарифмов, в качестве формы генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти цифровые суммы будут иметь случайное распределение, близкое к гауссову распределению.

Цифровая сумма двоичного представления числа известна как вес Хэмминга или численность населения. Алгоритмы выполнения этой операции были изучены, и она была включена в качестве встроенной операции в некоторые компьютерные архитектуры и некоторые языки программирования. Эти операции используются в вычислительных приложениях, включая криптографию, теорию кодирования и компьютерные шахматы.

Улучшение алгоритма вычисления цифрового корня

При расчёте цифрового корня можно воспользоваться небольшой хитростью: если значение не равно нулю, и не равно основанию системы счисления — 1, можно получить значение цифрового корня просто операцией взятия остатка от деления на основание системы счисления — 1.

Модифицированный код:

def digitalRoot(number, base):
    if number == 0:
        return 0
    dR = number % (base - 1)
    if dR == 0:
        dR = base - 1
    return dR

Свойства цифрового корня

Операция сложения

Сделаем небольшую таблицу, для того чтобы изучить закономерности, каким образом вычисляется цифровой корень суммы двух чисел:

Таблица для анализа операции цифрового корня суммы двух чисел.

Код для построения таблицы суммы:

firstTermRangeStart = 2
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10

for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
    print()
    for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
        if i % (secondTermRangeEnd + 1) == 0:
            print()
        print('dr(',j,'+', i, ') =', digitalRoot(j + i, base), ' ', end='')

Как можно увидеть, цифровой корень суммы чисел равен цифровому корню суммы цифровых корней этих чисел:

$dr_{base}(a1 + a2) = dr_{base}(dr_{base}(a1) + dr_{base}(a2))$

Операция вычитания

Формула похожа на предыдущую, однако совпадает не полностью.

Приведем контрпример: 455 — 123 = 332.

$dr_{10}(455)=5; dr_{10}(123) = 6; dr_{10}(322) = 8$

Как можно отметить, выражение 4 — 6 не даёт в результате 8, потому формулу сложения нужно модифицировать, чтобы она работала для операции вычитания:

$dr_{base}(a1 - a2) = dr_{base}(base - 1 + dr_{base}(a1) - dr_{base}(a2))$

Операция умножения

Выведем вариацию таблицы умножения, для того чтобы исследовать эту операцию:

Расчет цифрового корня от двух множителей

Код для вывода таблицы умножения:

firstTermRangeStart = 1
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10

for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
    print()
    for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
        print('dr(',j,'*', i, ') =', digitalRoot(i * j, base), ' ', end='')

Запишем значения для каждого множителя:

1) [1, 2, 3, 4, 5, 6, 7, 8, 9]

2) [2, 4, 6, 8, 1, 3, 5, 7, 9]

3) [3, 6, 9, 3, 6, 9, 3, 6, 9]

4) [4, 8, 3, 7, 2, 6, 1, 5, 9]

5) [5, 1, 6, 2, 7, 3, 8, 4, 9]

6) [6, 3, 9, 6, 3, 9, 6, 3, 9]

7) [7, 5, 3, 1, 8, 6, 4, 2, 9]

8) [8, 7, 6, 5, 4, 3, 2, 1, 9]

9) [9, 9, 9, 9, 9, 9, 9, 9, 9]

Можно увидеть, что последовательности разбиваются на пары 1 и 8, 2 и 7, 3 и 6, 4 и 5. В каждой из пар сохраняется та же самая последовательность, но они представляют собой реверсированные копии друг друга, за исключением последнего элемента, который связан с множителем, равным основанию системы счисления — 1.

Также отметим, что при умножении на основание системы счисления -1 цифровой корень будет равен основанию системы счисления — 1. При умножении на 1 значение цифрового корня второго множителя сохраняется.

Визуализация последовательностей:

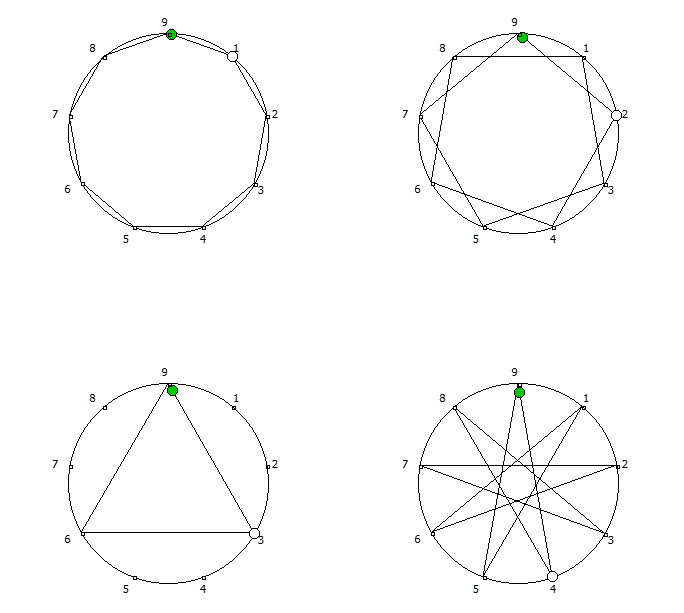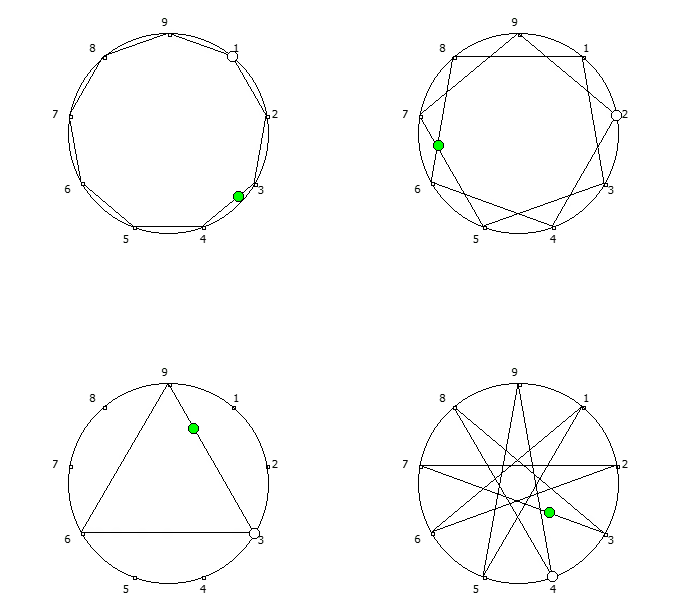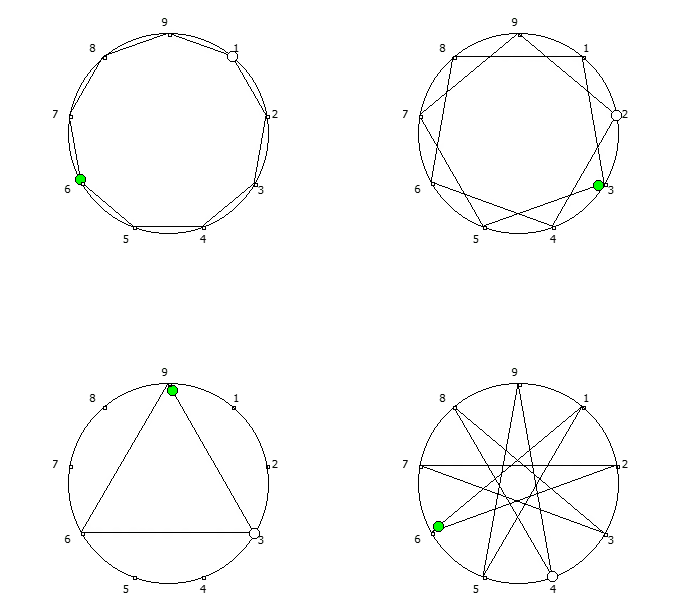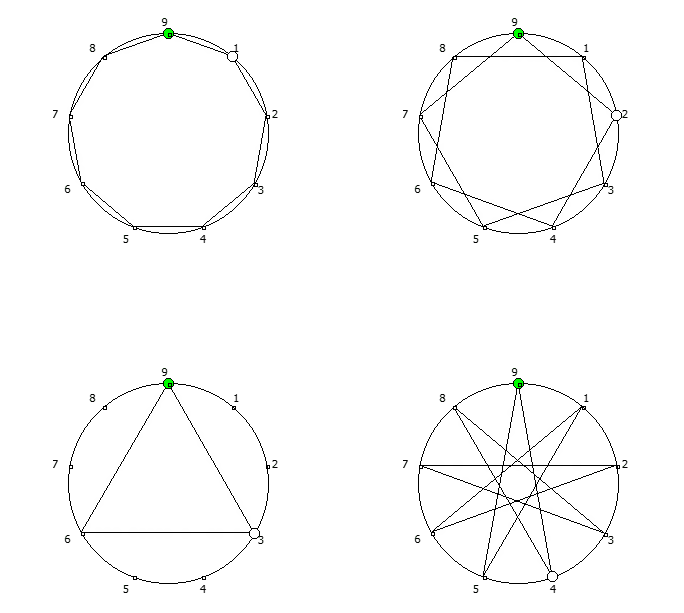Последовательности для множителей 1, 2, 3, 4. Они же являются зеркальными для 8, 7, 6, 5.

Последовательности можно рассмотреть как множество всех возможных замкнутых фигур с количеством точек, равным основанию системы счисления — 1, начиная с правильного n-угольника. Исключением является множитель, который не является взаимно простым с основанием системы счисления — 1, в данном случае это 3 и 6.

Для нахождения последовательности любой линии можно записать формулу:

$multiplicationLine(firstFactor, secondFactor, base) = firstFactor * secondFactor \mod base.$

Если записать эти значения как множество пересечений всех множителей, мы получим в результате ведический квадрат.

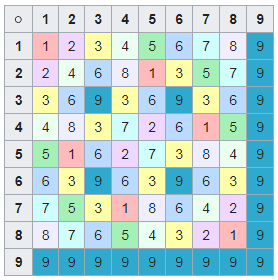Ведический квадрат для десятичной системы счисления.

Подмножество данного ведического квадрата формирует собой латинский квадрат. Чтобы получить его, нужно вычеркнуть элементы, равные основанию системы счисления — 1.

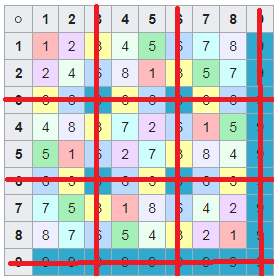Приведение ведического квадрата к латинскому квадрату в десятичной системе счисления.

В результате мы получим:

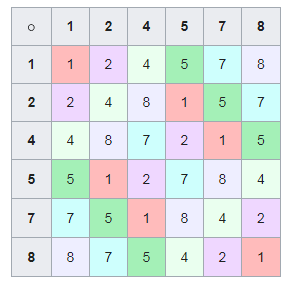Подмножество ведического квадрата, составляющее латинский квадрат в десятичной системе счисления.

Если переставить некоторые из его строчек местами, мы получим последовательность циклических чисел. О том, каким образом должны быть осуществлены перестановки строчек, будет рассказано ниже при исследовании других операций с цифровым корнем.

Ниже приведена ещё одна картинка ведических квадратов для систем счисления 100 и 1000. Белым отмечены самые большие значения клеток — соответствующие основанию системы счисления — 1, черным — самые маленькие, соответствующие 1.

Ведические квадраты для систем счисления 100 и 1000.

Теперь вернемся к произведению. Цифровой корень произведения одиночных цифр в заданной системе счисления вычисляется при помощи соответствующего ведического квадрата.

Для вычисления цифрового корня произведения двух чисел, которые содержат больше одной цифры, для начала нужно вычислить цифровой корень каждой из этих цифр, и после этого воспользоваться ведической площадью.

$dr_{base}(a1 * a2) = dr_{base}(dr_{base}(a1) * dr_{base}(a2))$

Операция деления

Рассмотрим те числа, которые дают при делении непериодические дроби, это 2, 5, 4, 8.

Для того чтобы быть уверенными, что мы не допускаем ошибок, воспользуемся уже выведенными правилами и умножим результат деления на 1000; так как цифровой корень 1000 равен 1, то произведение будет иметь тот же самый цифровой корень.

Таблица деления для делителей, которые взаимно просты с десятичной системой счисления.

base = 10
divisors = [2, 4, 5, 8]

for j in divisors: 
    print()
    for i in range(1, base):
        value = (digitalRoot(int((i / j) * (base ** 3)), base))
        print('dr(',i, '/', j, ') =', value, '  ', end='')

Тут бросаются в глаза несколько закономерностей. Число 9 не только при умножении, но и при делении приводит к значению цифрового корня, равному 9. Интересное происходит также с числами 3 и 6, эти числа как при умножении, так и при делении дают абсолютно одинаковые значения цифрового корня.

Запишем в таблицу череду делений:

2) [5, 1, 6, 2, 7, 3, 8, 4, 9] — Эта последовательность встречалась в множителе 5

4) [7, 5, 3, 1, 8, 6, 4, 2, 9] — Эта последовательность встречалась в множителе 7

5) [2, 4, 6, 8, 1, 3, 5, 7, 9] — Эта последовательность встречалась в множителе 2

8) [8, 7, 6, 5, 4, 3, 2, 1, 9] — Эта последовательность встречалась в множителе 8

Операция деления для цифрового корня определена только для делителей, которые не являются взаимно простыми с основанием системы счисления.

Операция возведения в степень

Таблица возведения в степень:

Таблица возведения в степень в десятичной системе счисления.

base = 10
.
for i in range(2, base - 2):
    print()
    for j in range(1, base - 1):
        print('dr(', j ,'^', i, ') =', digitalRoot(i ** j, base), ' ', end='')

Здесь мы можем наблюдать цикличность.

При внимательном рассмотрении других систем счисления можно сделать вывод, что эта череда связана с формированием остатков от деления, и таким образом она связалась с моим любимым классом простых чисел — full reptend prime.

Для того чтобы пояснить это, рассмотрим операции возведения в степень в других системах счисления. Забегая вперед, скажу: наиболее интересными будут являться такие степени счисления, которые равны p^n + 1, где p — это простое число, а n — натуральное.

Рассмотрим систему счисления 8, череда его значений будет равна [1, 3, 2, 6, 4, 5]. Именно такие же остатки от деления мы получаем при делении числа в десятичной системе счисления.

Деление 1 на 7 в столбик. Здесь мы можем наблюдать остатки от деления [1, 3, 2, 6, 4, 5].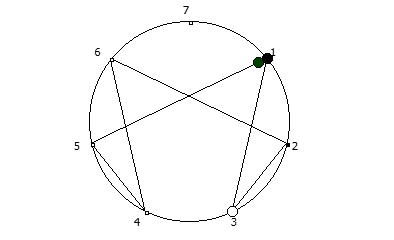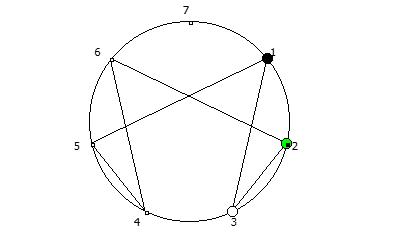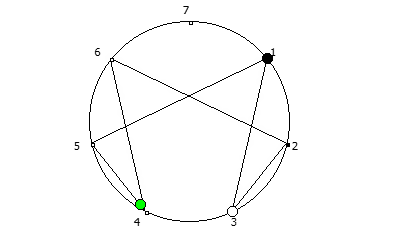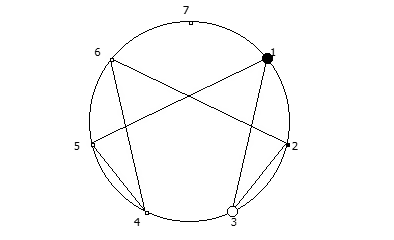

Последовательность полученная при возведении в степень, в восьмеричной системе счисления.

Это свойство связано с тем, что вычисление цифрового корня можно осуществить при помощи альтернативной формулы расчета цифрового корня:

$dr_{base}(n) = n - (base - 1) * \lfloor\frac{n-1}{base-1}\rfloor$

Ещё визуализации

Приведём ниже визуализации для операции возведения в степень для разных систем счисления, все они будут связанны с паттернами, образующимися в рациональных дробях 1/P, где P — это full reptend prime.

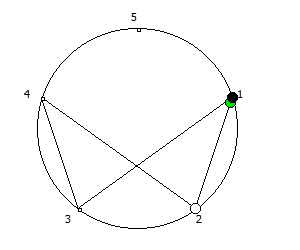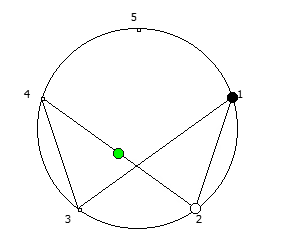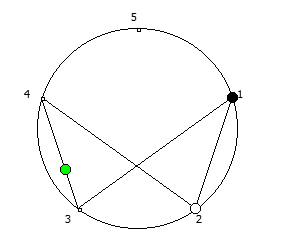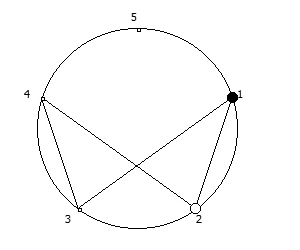Остатки от деления, найденные в 6 системе счисления, связанные с числом 5. 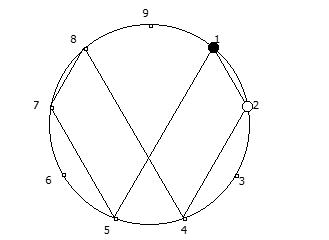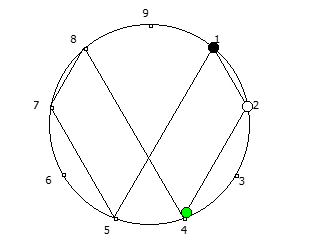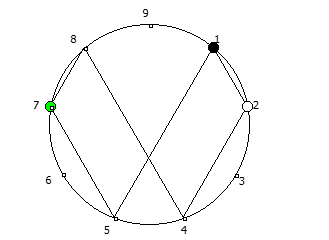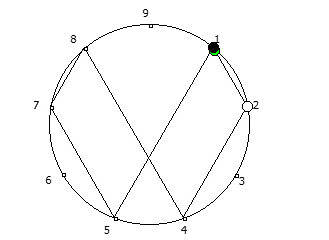Остатки от деления, найденные в 10 системе счисления, связанные с квадратом числа 3.

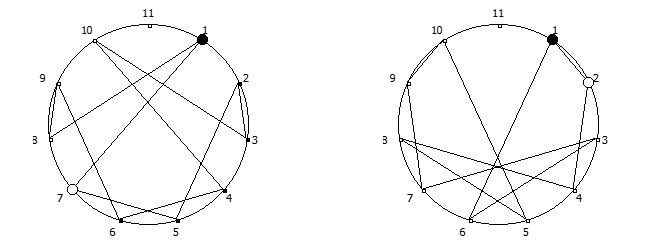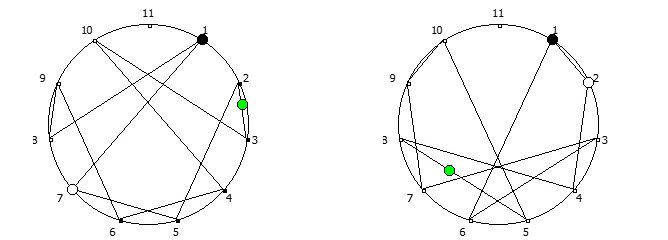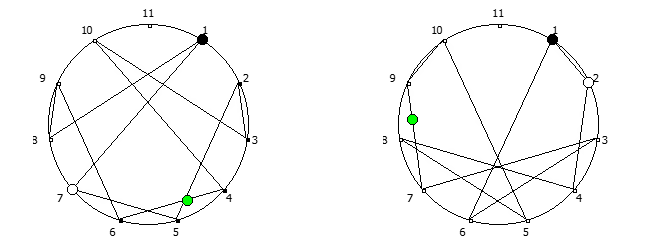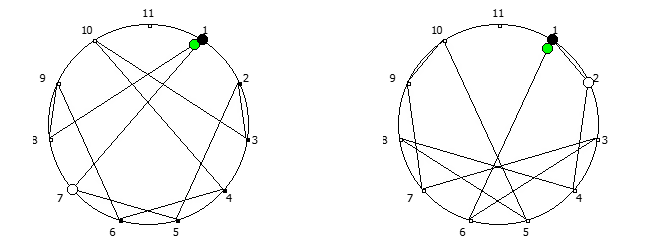Остатки от деления, найденные в 10 системе счисления, связанные с квадратом числа 3. Остатки от деления, найденные в 12 системе счисления, связанные с числом 11.

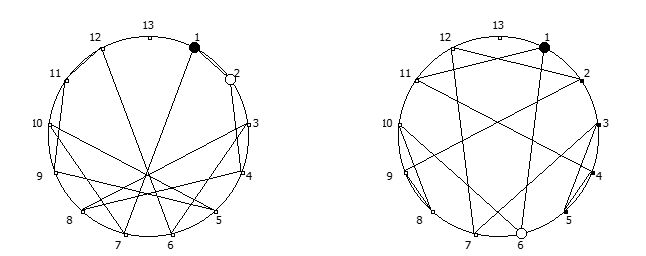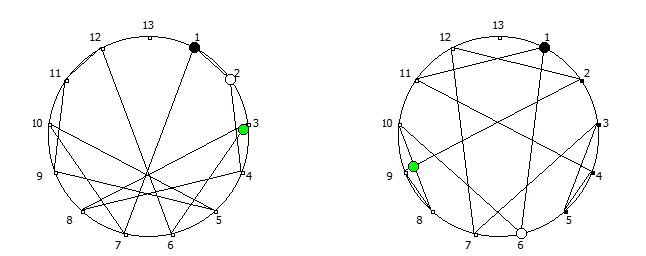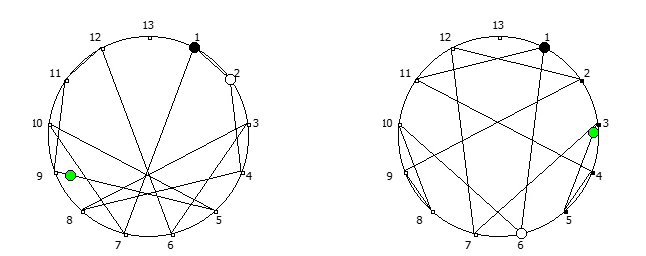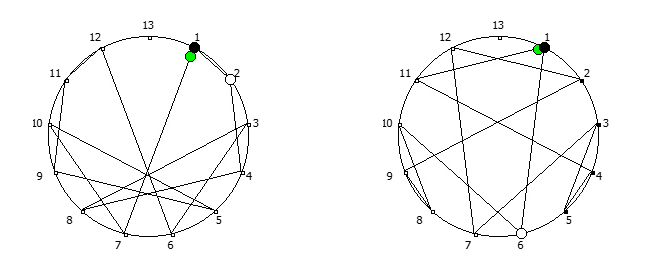Остатки от деления, найденные в 12 системе счисления, связанные с числом 11. Остатки от деления, найденные в 14 системе счисления, связанные с числом 13.

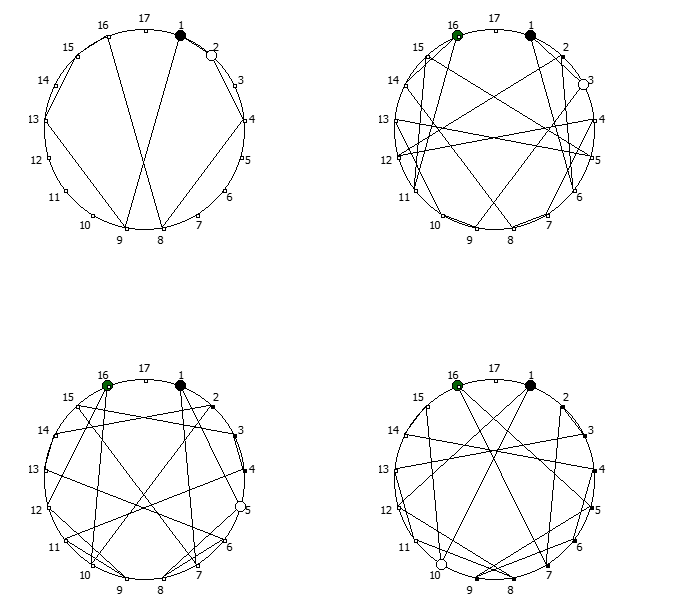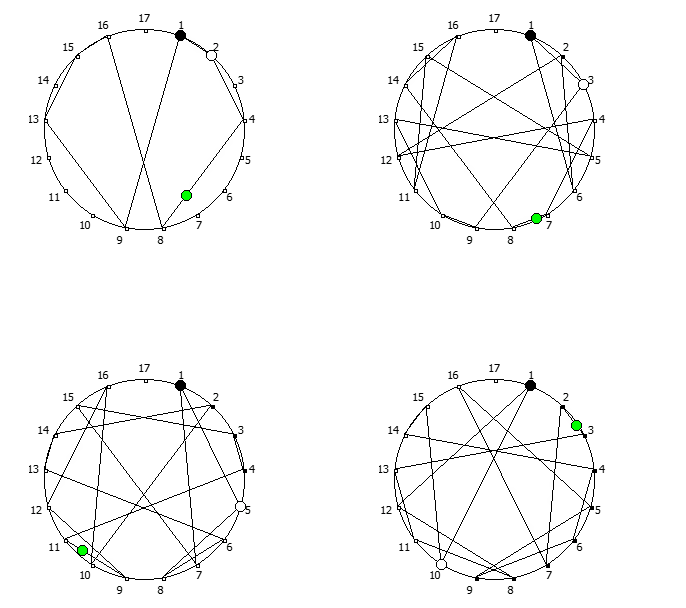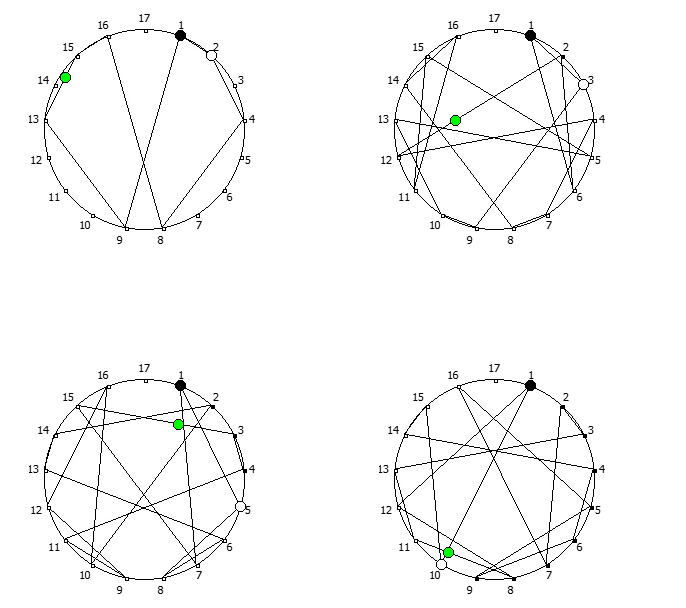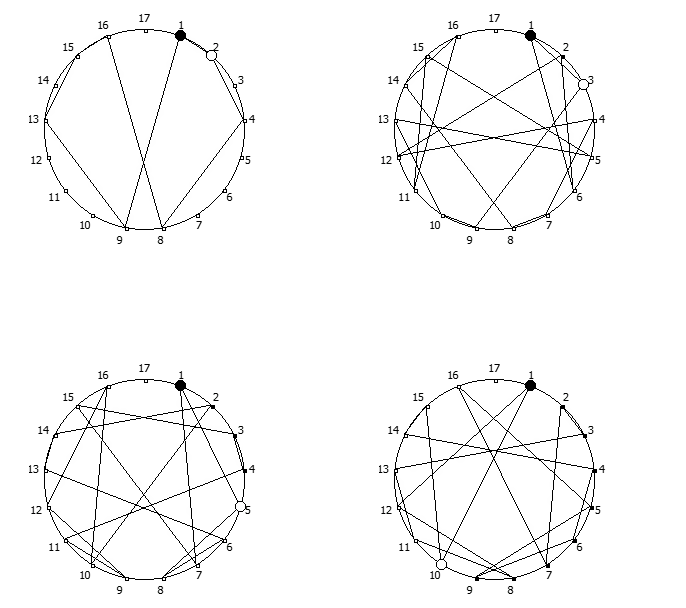Остатки от деления, найденные в 14 системе счисления, связанные с числом 13. Остатки от деления, найденные в 18 системе счисления, связанные с числом 17.

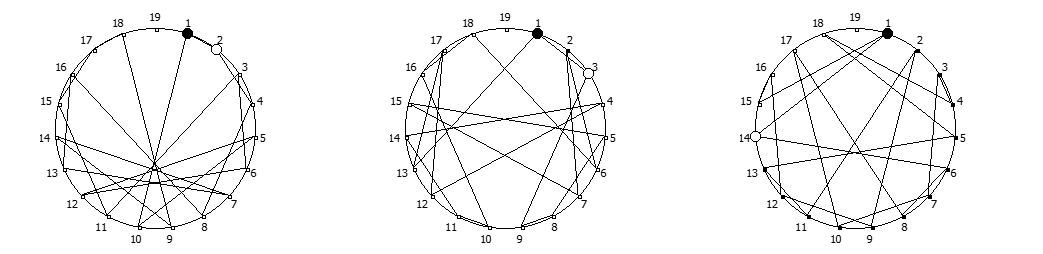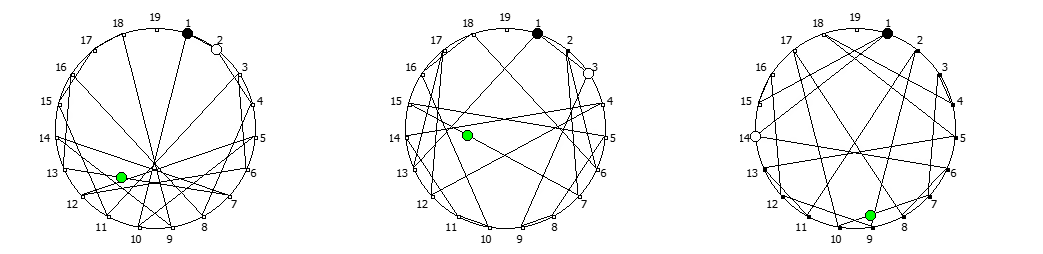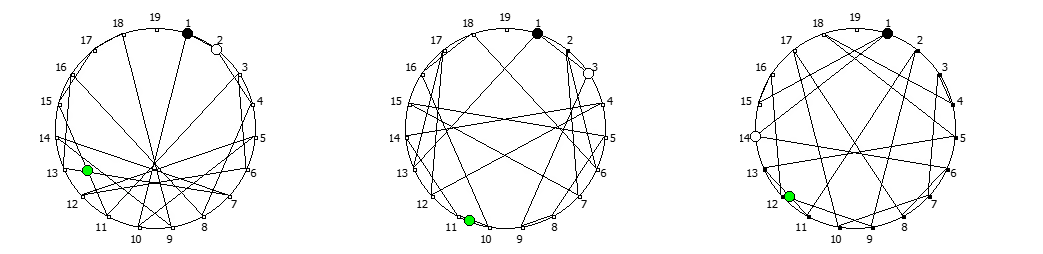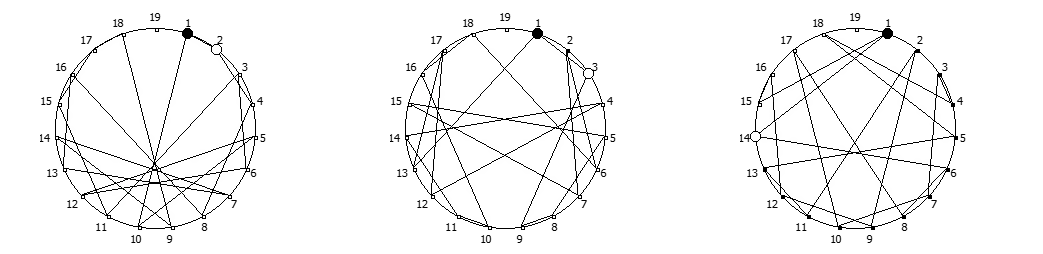Остатки от деления, найденные в 18 системе счисления, связанные с числом 17. Остатки от деления, найденные в 20 системе счисления, связанные с числом 19.

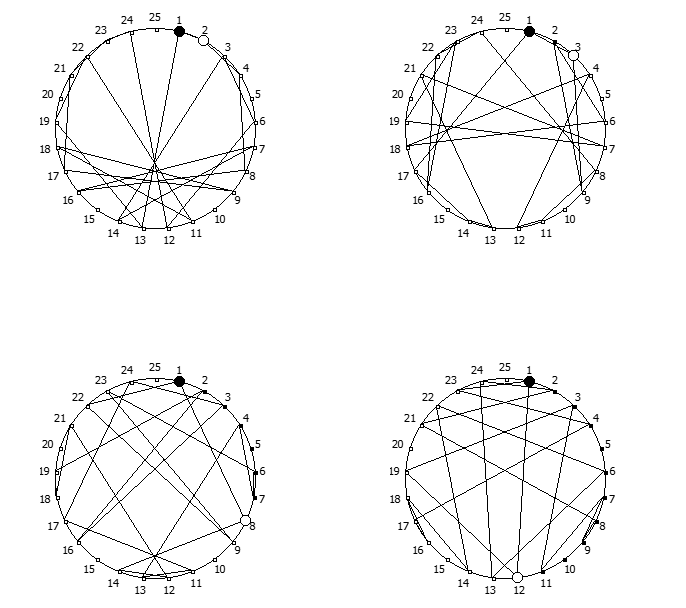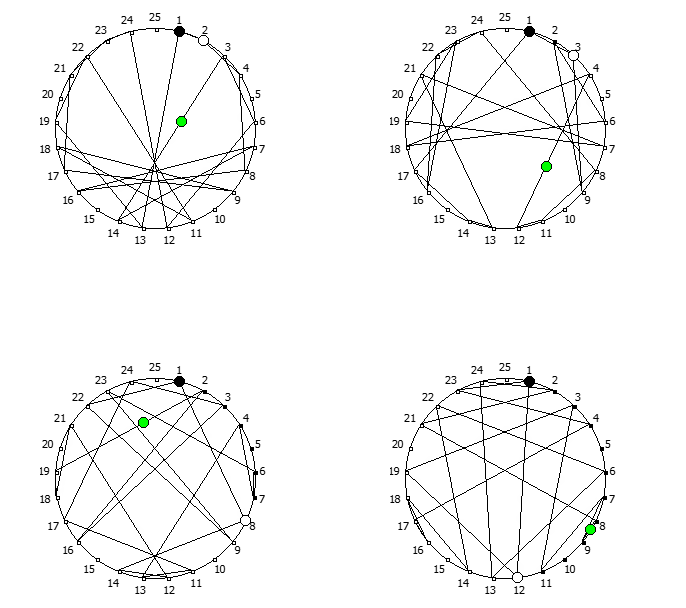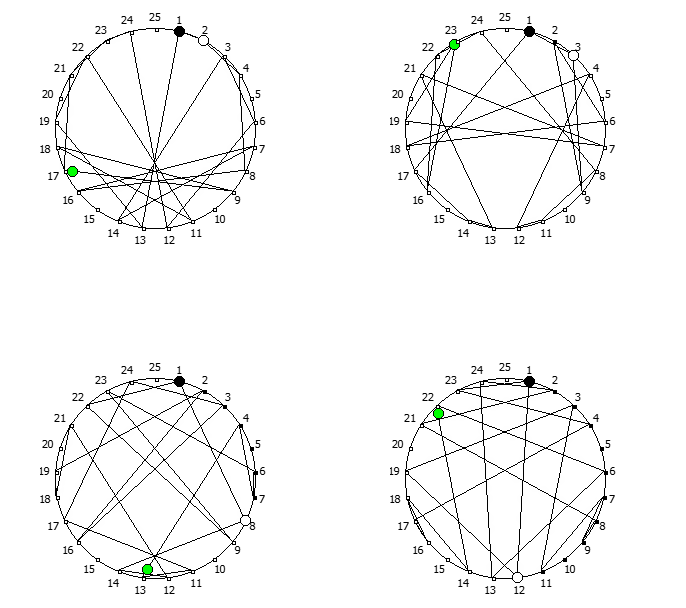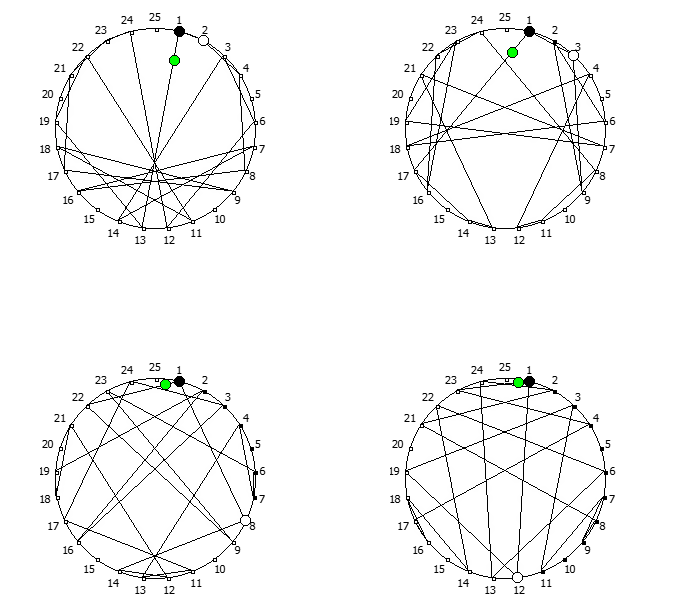Остатки от деления, найденные в 20 системе счисления, связанные с числом 19. Остатки от деления, найденные в 26 системе счисления, связанные с квадратом числа 5.

Остатки от деления, найденные в 26 системе счисления, связанные с квадратом числа 5. Остатки от деления, найденные в 28 системе счисления, связанные с кубом числа 3.

Остатки от деления, найденные в 28 системе счисления, связанные с кубом числа 3.

Теперь приведём несколько картинок из ведических квадратов, принцип их формирования очень прост, потому ограничимся небольшим количеством:

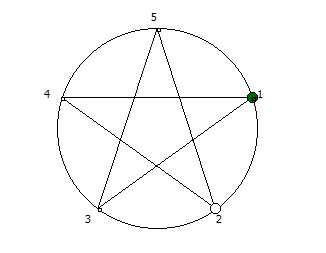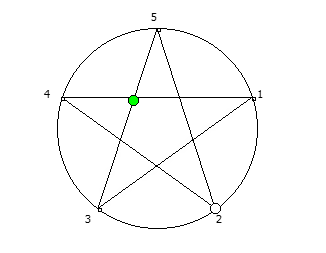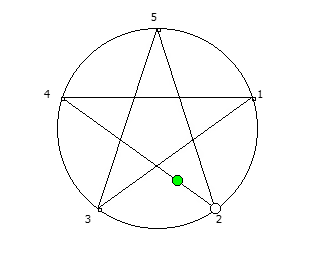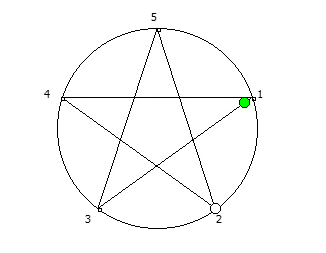Замкнутая фигура из 6 системы счисления, связана с числом 5. 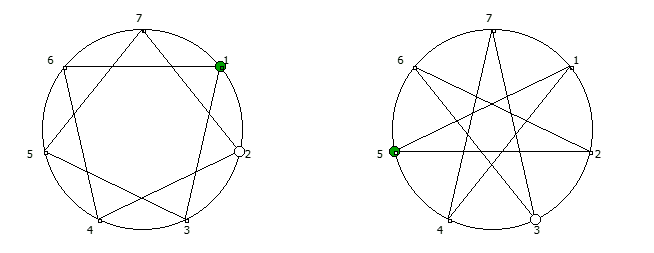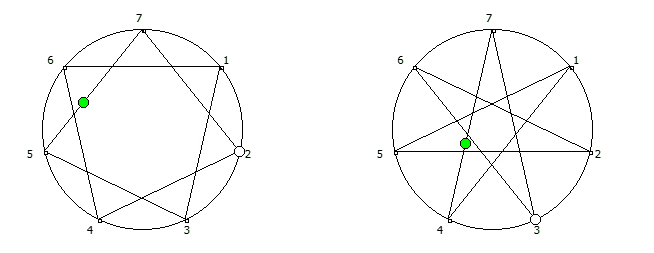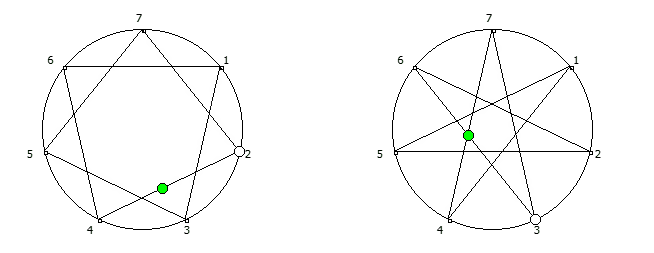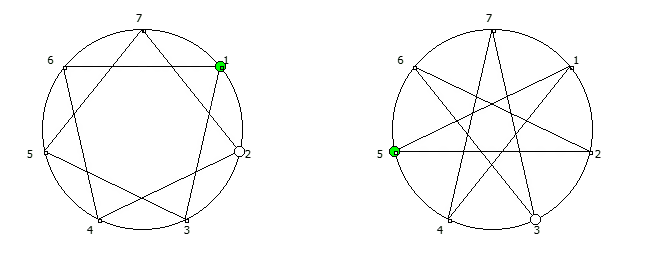Замкнутые фигуры из 8 системы счисления, связанные с числом 7.

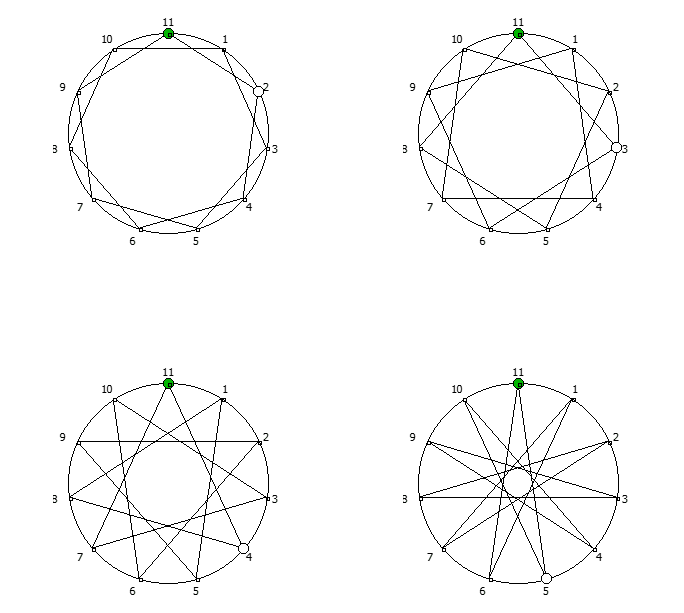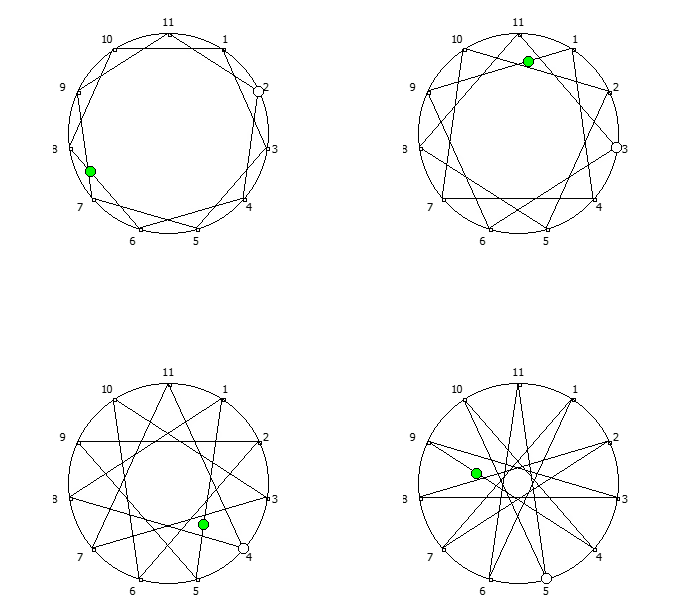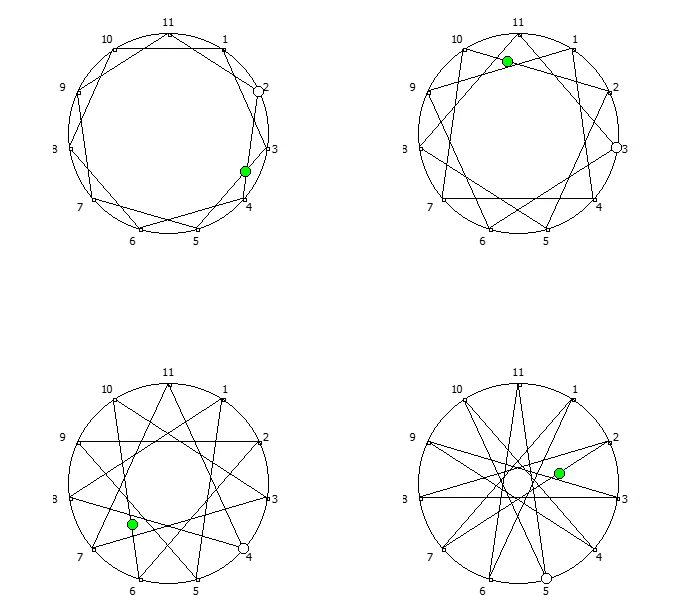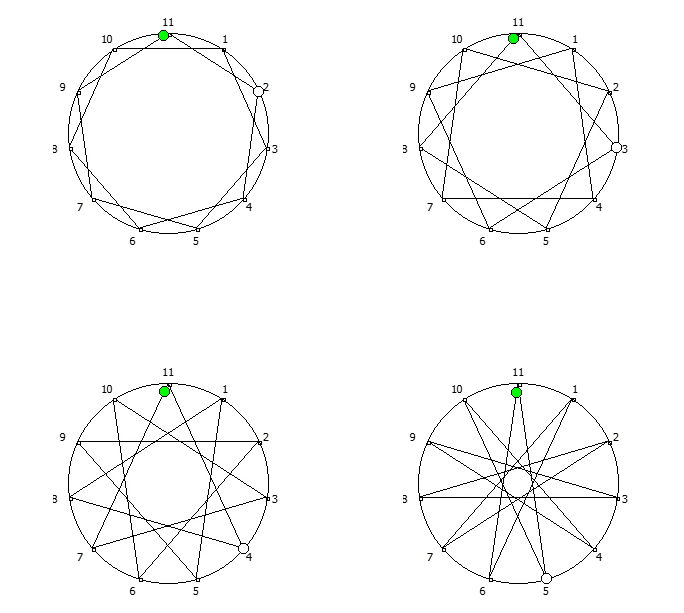Замкнутые фигуры из 8 системы счисления, связанные с числом 7. Замкнутые фигуры из 12 системы счисления, связанные с числом 11.

Замкнутые фигуры из 12 системы счисления, связанные с числом 11.

Образование циклических чисел при помощи ведической площади и остатков от деления

После того как мы получили латинский квадрат из ведического квадрата, пронумеруем его строки последовательно:

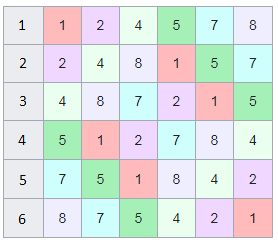Пронумерованный латинский квадрат.

Теперь мы можем переставить строки на основании череды остатков от деления, таким образом мы получим последовательность циклических чисел. Напомню, остатки от деления были равны [1, 3, 2, 6, 4, 5]. В результате у нас получится следующая картина:

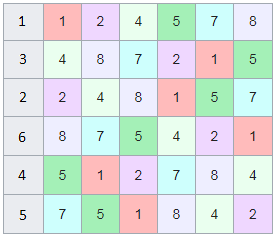Перестановки в пронумерованном латинском квадрате, в результате мы получили циклическое число.

Как можно наблюдать, первый столбец теперь представляет собой циклическое число 142857.

Выводы

Несмотря на плохую репутацию нумерологии, операции суммы цифр и цифрового корня имеют пусть не широкое, но всё же практическое применение.

Например, с помощью цифрового корня можно сформировать множество замкнутых n-вершинных звезд, многие из которых очень любят современные рок\метал группы :)

Пентаграмма — в представлении не нуждается :) Уроборос тут не случайно, о нем в следующей статье!

Tool предпочитают 8 систему счисления, связанную с простым числом 7. Slipknot тяготеют к десятеричной системе счисления, связанной с квадратом числа 3.

Slipknot тяготеют к десятеричной системе счисления, связанной с квадратом числа 3.

Как можно видеть, многие метал группы тоже любят теорию чисел!

Но лично я для своей метал группы решил выбрать анимированный логотип, составленный из одновременной визуализации периодических дробей, образованных из 90 рациональных дробей 1/91…90/91:

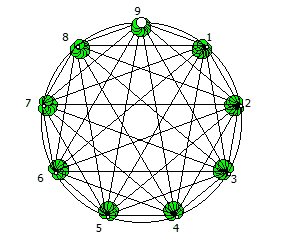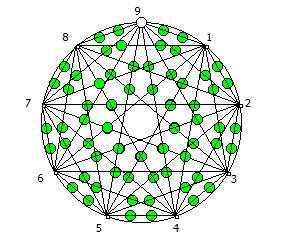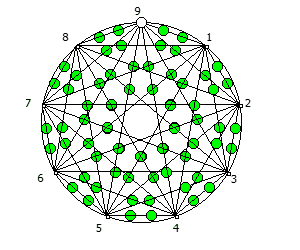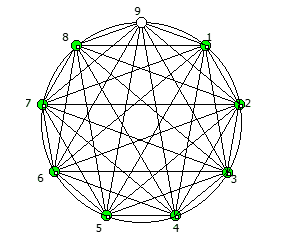Почему я выбрал число 91, которое является произведением 7 и 13? Речь об этом пойдет в следующей статье:)

Если у кого-то есть дополнительная информация об описанных выше понятиях, пожалуйста присылайте её в комментарии, я буду очень благодарен!

Надеюсь, что вам было интересно, большое спасибо за внимание!