Нобелевский лауреат по (математике?) о «Моде, вере, фантазии и новой физике Вселенной»
Роджер Пенроуз стал лауреатом Нобелевской премии по физике 2020 года «за открытие того, что образование черных дыр является надежным предсказанием общей теории относительности».
Также Нобелевской премии по физике были удостоены Рейнхард Генцель и Андреа Гез «за открытие сверхмассивного компактного объекта в центре нашей галактики».
Роджер Пенроуз — член Лондонского королевского общества. Работает в различных областях математики, общей теории относительности и квантовой теории. Пенроуз — автор теорий, связанных с квантовым сознанием, квантовым скачком, квантовой биологией, автор книги «Мода, вера, фантазия и новая физика Вселенной», изданной в Издательстве «Питер».
Книга «Мода, вера, фантазия и новая физика Вселенной» основана на материале трех лекций, прочитанных Пенроузом в Принстонском университете. Автор и сам признает, что обычно мода, фантазия и вера совершенно не волнуют людей, всерьез изучающих первоосновы мироздания. Веру оставим церквям, моду — показам кутюрье, фантазию — писателям. Роджер Пенроуз на 500 страницах доказывает, что эти романтические слова могут быть важными в поисках фундамента Вселенной.
Фантазия
3.1. Большой взрыв и вселенные Фридмана
Может ли фантазия играть какую-либо неиллюзорную роль в наших попытках понять физическую реальность? Определенно, фантазия — полная противоположность науки как таковой, и ей не место в серьезном научном дискурсе. Однако остается ощущение, что от этого вопроса не так легко отмахнуться, как могло бы показаться, — многие природные процессы покажутся фантастичными, если исходить из выводов, к которым может привести нас рациональный научный опыт, основанный на надежных экспериментальных исследованиях. Как мы убедились, особенно в предыдущей главе, мир действительно устроен самым фантастическим образом, если изучать его на микроуровне, где царят квантовые явления. Конкретный материальный объект может находиться в нескольких местах и, подобно сказочному вампиру (способному превращаться из летучей мыши в человека и обратно, когда ему вздумается), может проявлять то корпускулярные, то волновые свойства словно по собственному выбору. При этом его «поведение» подчиняется таинственным числам, в которых содержится мнимый квадратный корень из –1.
Более того, в предельно крупных масштабах опять обнаруживаются явления, многие из которых могут показаться фантастическими — возможно, даже поразительнее всех находок литературной фантастики. Например, иногда наблюдается столкновения между целыми галактиками, и приходится считать, что они неотвратимо поглощают друг друга (а мы фиксируем это по возникающим искажениям пространства-времени, провоцируемым обеими галактиками).
Действительно, такие искажения пространства-времени иногда можно наблюдать даже напрямую — по грубому искривлению снимков очень отдаленных галактик. Вдобавок самые экстремальные из известных нам искажений пространства-времени могут приводить к возникновению массивных черных дыр в космическом пространстве: недавно удалось наблюдать, как две такие дыры поглощают друг друга и образуют еще более крупную [Abbott et al., 2016]. Есть черные дыры, которые в миллионы или десятки тысяч миллионов раз тяжелее Солнца, поэтому такие дыры могли бы с легкостью заглатывать целые солнечные системы. Тем не менее эти монстры весьма малы по сравнению с самими галактиками, в центрах которых они и обретаются. Часто такая черная дыра выдает свое существование, порождая два коллимированных пучка высокоэнергетических частиц. Эти пучки исторгаются из черной дыры в противоположных направлениях из крошечного центрального региона той галактики, в которой сидит эта дыра; частицы летят со скоростью, которая может достигать до 99,5% скорости света [Tombesi et al., 2012; Piner, 2006]. Однажды удалось наблюдать, как такой пучок вылетел из одной галактики и прицельно попал в другую, как будто эта была колоссальная межгалактическая война.
В еще более крупных масштабах обнаруживаются целые регионы, заполненные невидимым нечто, пронизывающим космос. Складывается впечатление, что на эту совершенно неизвестную субстанцию приходится около 84,5% всей материи, имеющейся во Вселенной. При этом существует еще что-то, достигающее самых дальних пределов наблюдаемой Вселенной и словно растаскивающее ее в разные стороны с нарастающей скоростью. Словно от безысходности ученые дали двум этим сущностям довольно туманные названия — «темная материя» и «темная энергия» соответственно. Именно темная материя и темная энергия в основном определяют общую структуру известной Вселенной. Еще тревожнее кажется следующий факт: современная космология почти наверняка доказывает, что вся известная нам Вселенная возникла из одного гигантского взрыва, до которого совсем ничего не было — если вообще можно говорить о чем-то «до» возникновения пространственно-временного континуума, который, как мы полагаем, лежит в основе всей материальной реальности. Поистине, такая концепция Большого взрыва — фантастическая идея!
Так и есть;, но в нашем распоряжении все больше эмпирических доказательств в пользу того, что на заре существования наша Вселенная действительно была невероятно плотной и стремительно расширялась. В ней было заключено не только все материальное содержимое того космоса, который нам известен, но и все пространство-время, на фоне которого сейчас разыгрывается бытие физической реальности и которое, по-видимому, неограниченно далеко простирается во все стороны. Все, что нам известно, по-видимому, возникло в результате этого Большого взрыва. Каковы доказательства? Мы должны оценить достоверность этой идеи и попытаться понять, куда она может нас привести.
В этой главе мы обсудим некоторые современные идеи, касающиеся происхождения самой Вселенной, и в частности коснемся следующей проблемы: в какой степени оправданно прибегать к фантазиям для объяснения эмпирических фактов. В последние годы многочисленные эксперименты действительно дали нам огромные объемы данных, непосредственно значимых для понимания истоков Вселенной. Вещи, которые ранее казались набором в основном непроверенных спекуляций, перешли в категорию точной науки. Важнее всего упомянуть спутники COBE, запущенный в 1989 году, WMAP, запущенный в 2001 году, а также космическую обсерваторию им. Планка, которая работает с 2009 года. Упомянутые спутники постепенно исследовали реликтовый космический микроволновый фон (см. раздел 3.4) все подробнее и подробнее. Однако нерешенные вопросы остаются, и в поисках ответов на них некоторые специалисты по теоретической космологии углубились в дебри, которые вполне уместно назвать совершенно фантастическими.
Да, в некоторой степени фантазия, безусловно, оправданна, но не слишком ли рьяно устремились современные теоретики в этом направлении? В разделе 4.3 я озвучу мою собственную довольно нетрадиционную версию, позволяющую разрешить многие из этих загадок. Идеи, на которых замешан мой ответ, кому-то также могут показаться дикими, и я вкратце опишу, почему их следовало бы воспринимать всерьез. Тем не менее в этой книге меня больше интересуют устоявшиеся к настоящему времени представления о самых ранних этапах эволюции нашей замечательной Вселенной, и я хотел бы обсудить, насколько правдоподобны отдельные направления, в которых ведут свои исследования некоторые современные космологи.
Для начала у нас есть величественная эйнштейновская общая теория относительности, которая, насколько известно, исключительно точно описывает структуру нашего искривленного пространства-времени и движение небесных тел (см. разделы 1.1 и 1.7). В 1922 и 1924 годах вслед за первыми попытками Эйнштейна применить эту теорию для описания целостной структуры Вселенной русский математик Александр Фридман впервые нашел решения для эйнштейновских уравнений поля в контексте пространственно однородного (гомогенного и изотропного) распределения расширяющейся материи, причем приблизительной моделью такой материи считалась идеальная жидкость (пылевое решение), представляющая усредненное распределение массы-энергии галактик [Rindler, 2001; Wald, 1984; Hartle, 2003; Weinberg, 1972]. Действительно, с эмпирической точки зрения кажется, что в таком случае получается достаточно хорошее общее приближение к усредненному распределению материи в существующей Вселенной, и выводится тензор энергии T, который был необходим Фридману для представления гравитации в уравнении Эйнштейна G=8πעT+Λg (см. раздел 1.1). Характерная черта моделей Фридмана заключается в том, что расширение начинается с сингулярности (теперь этот момент именуется Большим взрывом). Тогда кривизна пространства-времени была бесконечной, а плотность массы-энергии источника материи T устремлялась бы в бесконечность, если бы мы попытались отмотать время назад до этой пространственно-временной сингулярности.
(Удивительно, что общеупотребительный ныне термин «Большой взрыв» задумывался как уничижительный; придумал его Фред Хойл, ярый сторонник альтернативной теории стационарной Вселенной; см. раздел 3.2.) Он впервые упомянул слова «Большой взрыв» в радиоинтервью компании BBC — серию таких выступлений он сделал в 1950 году. В разделе 3.10 эти интервью упоминаются и в ином контексте; позже на их основе была составлена книга [Hoyle, 1950].
Пока я стану условно считать, что очень малая эйнштейновская космологическая постоянная Λ — именно она и обусловливает ускоряющееся расширение Вселенной, упомянутое ранее (см. также раздел 1.1), — равна нулю. Тогда нам потребуется рассмотреть всего три отдельные ситуации, определяемые пространственной геометрией: кривизна пространства K может быть положительной (K > 0), нулевой (K = 0) или отрицательной (K < 0). В авторитетных книгах по космологии принято нормировать величину K, приводя ее к одному из трех значений: 1, 0, –1. Здесь рассказ будет понятнее, если считать K вещественным числом, характеризующим фактическую кривизну пространства. Мы можем представлять K как величину, указывающую такую пространственную кривизну в какой-то специально подобранный момент времени t. Например, можно условиться, что t будет соответствовать эпохе последнего рассеяния (см. раздел 3.4), когда образовался космический микроволновый фон, но выбор конкретного момента в данном случае не важен. Суть в том, что знак K не будет меняться со временем, поэтому положительное, отрицательное или нулевое значение K характеризует модель в целом, независимо от выбранного «момента отсчета».
Однако следует отметить, что значение K само по себе не вполне характеризует геометрию пространства-времени. Также существуют нестандартные «свернутые» варианты таких моделей, пространственная геометрия которых бывает довольно сложной, причем в некоторых примерах Вселенная может быть конечной, даже если K = 0 или K < 0. Некоторые ученые интересовались
такими моделями (см. Levin [2012], Luminet et al., [2003], исходно Schwarzschild [1900]). Однако здесь эти модели для нас не важны; эта проблема существенно не влияет на большинство аргументов, которые я в данном случае излагаю. Если не учитывать топологические сложности, то у нас получится всего три типа однородной геометрии, которые (на плоскости) очень красиво изображал голландский художник М.К. Эшер (рис. 3.1; ср. также с рис. 1.38 в разделе 1.15). Трехмерная картина выглядит так же.
Проще всего понять случай K=0, так как в этом случае пространственное сечение будет представлять собой обычное трехмерное евклидово пространство, хотя, чтобы описать расширяющуюся Вселенную, нам понадобится множество таких последовательных сечений: см. рис. 3.2 б. (Это расширение можно понимать в терминах расходящихся времениподобных линий, которые соответствуют мировым линиям идеализированных галактик, описываемых этой моделью. Это будут линии времени, о которых мы поговорим далее.)Трехмерные пространства, являющиеся пространственными сечениями в случае K > 0, представить немного сложнее, поскольку они являются 3-сферами (
), каждая из которых в трех измерениях аналогична двумерной поверхности обычной сферы (
), а расширение Вселенной выражается как увеличение радиуса сферы со временем (рис. 3.2 а). В случае отрицательной кривизны (K
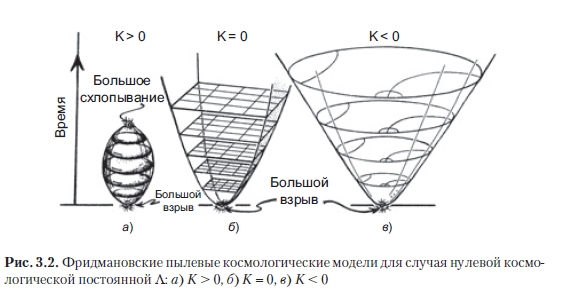
Термин «конформная», применяемый в этих моделях, употребляется потому, что в гиперболической геометрии величина угла между двумя гладкими кривыми в точке их пересечения будет такой же, как и в фоновой евклидовой геометрии (так, например, углы на кончиках рыбьих плавников на рис. 1.38 a или крылья чертей на рис. 3.1 в представлены без искажений, независимо от того, как близко к ограничивающей окружности они расположены). Другая (грубая) формулировка того же принципа звучит следующим образом: формы (но не размеры) очень мелких деталей в таких представлениях всегда отображаются без искажений (см. также рис. A.39 в разделе A.10).
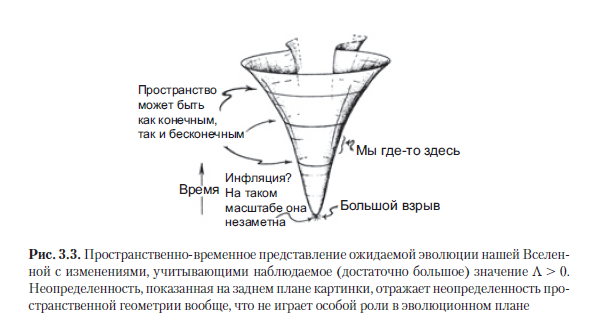
Как отмечалось ранее, уже найдены некоторые убедительные доказательства того, что в нашей Вселенной космологическая постоянная Λ имеет небольшое положительное значение, поэтому мы должны рассматривать фридмановские модели, соответствующие Λ > 0. На самом деле, как ни ничтожна Λ, ее значение все-таки достаточно велико (при этом, согласно уравнениям Эйнштейна, мы продолжаем считать ее константой), чтобы преодолеть коллапс и «большое схлопывание», показанное на рис. 3.2 a. Вместо этого при всех трех возможных вариантах значения K, допускаемых современными наблюдениями, Вселенная в итоге должна пуститься в расширение с ускорением. При такой положительной постоянной Λ расширение Вселенной будет продолжаться до бесконечности и в конечном итоге станет экспоненциальным (см. рис. A.1 в разделе A.1). Согласно таким выкладкам мы представляем себе общую историю Вселенной такой, как показано на рис. 3.3. Задний план изображен неопределенно, чтобы показать, что наблюдения допускают все три варианта пространственной кривизны K.
Варианты отдаленного будущего во всех этих моделях при Λ > 0 даже при наличии в них некоторых нерегулярностей очень похожи и хорошо описываются конкретной пространственно-временной моделью, которая называется де-ситтеровским пространством. Тензор Эйнштейна Т в нем равен просто Λg. Эта модель была найдена Виллемом де Ситтером (и независимо от него Туллио Леви-Чивитой) в 1917 году (см. [de Sitter, 1917a, b; Levi-Cività, 1917; Schrödinger, 1956]; ПкР, п. 28.4). В настоящее время принято считать, что эта модель хорошо аппроксимирует отдаленное будущее именно нашей Вселенной, когда тензор энергии полностью определяется Λ, поэтому в предельно далеком будущем сложится ситуация G≈Λg.
Разумеется, при этом мы предполагаем, что эйнштейновские уравнения (G=8πעT+Λg) будут действовать неограниченно долго и значение Λ, определенное в наше время, останется константой. В разделе 3.9 будет показано, что, согласно экзотическим идеям инфляционной космологии, модель де Ситтера должна была описывать Вселенную и на значительно более раннем этапе, непосредственно после Большого взрыва, однако значение Λ на тот момент должно было колоссально превышать нынешнее. Эти вопросы обретут для нас важность позднее (см. разделы 3.7–3.9 и 4.3), а пока мы не будем подробно на них останавливаться.
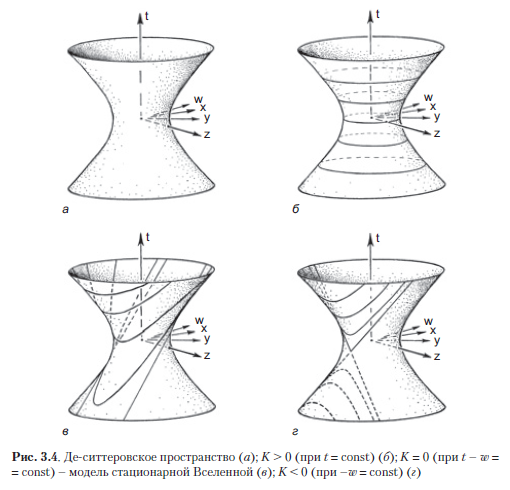
Де-ситтеровское пространство — это высокосимметричное пространство-время, которое можно описать как (псевдо-)сферу в пятимерном пространстве Минковского (рис. 3.4 a). Эта (псевдо-)сфера возникает в точке 
= –3/Λ, получая локальную метрическую структуру от охватывающего пятимерного пространства Минковского с координатами (t, w, x, y, z) (Те, кто знает, как стандартным образом записываются метрики при помощи дифференциалов, понимают, что эта пятимерная метрика Минковского приобретает вид 
=
.) Де-ситтеровское пространство полностью повторяет симметрию четырехмерного пространства Минковского; в обоих случаях имеем 10-параметрическую группу симметрий. Также можно вспомнить гипотетическое анти-де-ситтеровское пространство, рассмотренное в разделе 1.15. Оно весьма тесно связано с де-ситтеровским пространством и обладает группой симметрии такого же порядка.
Де-ситтеровское пространство — пустая модель, в которой тензор энергии T равен нулю, поэтому там нет никаких (идеализированных) галактик, которые могли бы определять линии времени, чьи ортогональные трехмерные пространственные сечения позволяли бы определять конкретные трехмерные геометрии «синхронного времени». На самом деле, довольно примечателен факт: оказывается, в де-ситтеровском пространстве можно выбирать такие трехмерные пространственные сечения (с синхронным временем) тремя принципиально разными способами, так что де-ситтеровское пространство можно интерпретировать как равномерно расширяющуюся в пространстве Вселенную с каждым из трех альтернативных типов пространственной кривизны в зависимости от того, каким образом ее рассекают такие трехмерные сечения, соответствующие одному и тому же космическому времени: K > 0 (при t = const), K = 0 (при t — w = const) и K < 0 (при –w = const) (рис. 3.4 б–г). Это смог красиво продемонстрировать Эрвин Шрёдингер в своей книге «Расширяющиеся вселенные» (1956). Более ранняя модель стационарной Вселенной, которую мы обсудим в разделе 3.2, описывается пространством де Ситтера в соответствии с сечением K = 0, показанным на рис. 3.4 в (и конформно представленным на рис. 3.26 б в разделе 3.5). В большинстве версий инфляционной космологии (до которой мы дойдем в разделе 3.9) также используется такое сечение K = 0, поэтому инфляция может однородно и экспоненциально продолжаться в течение неограниченного времени.
На самом деле, что касается крупномасштабной структуры нашей реальной Вселенной, современные наблюдения не позволяют однозначно ответить, какой из этих вариантов пространственной геометрии точнее всего ее описывает. Тем не менее каков бы ни был окончательный ответ, сейчас не кажется, что вариант K = 0 так уж близок к истине (примечательно, особенно с учетом на первый взгляд убедительных доказательств в пользу K 0, это будет подлинно важно с философской точки зрения, поскольку будет означать, что пространственные размеры Вселенной конечны. Однако по состоянию на настоящий момент принято просто утверждать следующее: согласно наблюдениям K = 0. Это может быть очень хорошим приближением, но в любом случае мы не знаем, насколько близка реальная Вселенная к подлинной пространственной однородности и изотропии, особенно с учетом определенных противоречивых данных, полученных при наблюдении космического микроволнового фона (например, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).
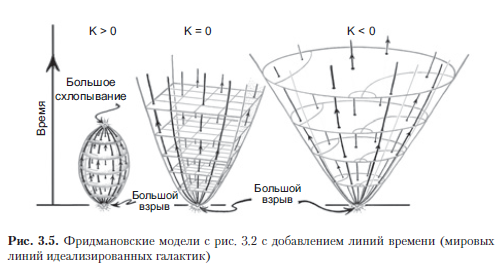
Для того чтобы построить картину полного пространства-времени в соответствии с фридмановскими моделями и их обобщениями, нужно знать, как будут со временем изменяться «размеры» нашей пространственной геометрии, причем с самого начала. В стандартных космологических моделях, например у Фридмана, либо в обобщенных моделях, вкратце именуемых ФЛРУ (Фридмана — Леметра — Робертсона — Уокера), — во всех моделях этого общего класса пространственные сечения однородны и изотропны и полное пространство-время обладает такой же симметрией, как и сами сечения. В них есть четкое определение космического времени t, которое описывает эволюцию такой вселенской модели. Данное космическое время стартует в момент t = 0(Большой взрыв) и отсчитывается идеализированными часами, следующими по мировым линиям идеализированных галактик (рис. 3.5, а также рис. 1.17 в разделе 1.7). Я буду именовать эти мировые линии линиями времени в модели ФЛРУ (в работах по космологии они также иногда называются мировыми линиями фундаментальных наблюдателей). Линии времени — это геодезические кривые, ортогональные пространственным сечениям, которые, в свою очередь, являются 3-плоскостями с одинаковым значением t.
Случай де-ситтеровского пространства имеет важную особенность: поскольку, как упоминалось ранее, пространство пустое, то есть тензор энергии-импульса T в уравнении G=8πT+Λg равен нулю, то у нас нет никаких мировых линий, связанных с материальными телами, которые позволили бы нам определить временные линии или, соответственно, пространственную геометрию. Поэтому локально у нас есть выбор, как трактовать данную модель описания Вселенной: соответствует ли она K > 0, K = 0 или K< 0. Тем не менее глобально эти три ситуации различаются, что видно на рис. 3.4 б–г: в каждом из этих случаев нарезка захватывает иную часть целостного де-ситтеровского пространства. Далее
я буду исходить из того, что T не равен нулю и обеспечивает положительную плотность энергии вещества, что позволяет хорошо определить и линии времени, и пространственноподобные 3-поверхности постоянного времени для каждого значения t, как показано на рис. 3.2.
В случае с положительной кривизной пространства (K > 0) в стандартной Вселенной Фридмана, наполненной пылью, охарактеризовать ее «размер» можно, используя радиус R 3-сферических пространственных сечений, и исследовать этот размер как функцию t. При Λ = 0 находим функцию R (t), описывающую циклоиду в плоскости (R, t) (при этом скорость света принимается за единицу: c = 1). Циклоида — это кривая с простой геометрической характеристикой: она описывается точкой окружности, катящейся по оси t (рис. 3.6 б). Отметим, что (после момента времени 
) значение R вновь достигает нуля, как и при Большом взрыве, поэтому вся модель Вселенной с 0 вновь схлопывается в сингулярность, и этот момент часто именуется большим схлопыванием.
В оставшихся случаях K < 0 и K = 0 (с нулевой Λ) Вселенная будет бесконечно расширяться и большого схлопывания не будет. В случае K < 0 есть «радиус», аналогичный R, но для K = 0 можно просто выбрать произвольную пару мировых линий идеализированных галактик и взять в качестве R отрезок, разделяющий их в пространстве. В случае K = 0 скорость расширения асимптотически стремится к нулю, а в случае K < 0 — к некоторому положительному значению.
Современные наблюдения свидетельствуют в пользу того, что Λ, скорее всего, положительно и его величина достаточна, чтобы играть решающую роль в скорости расширения Вселенной, поэтому значение K утрачивает важность для этой динамики, и Вселенная в конечном итоге срывается в ускоренное расширение, как показано на рис. 3.3.
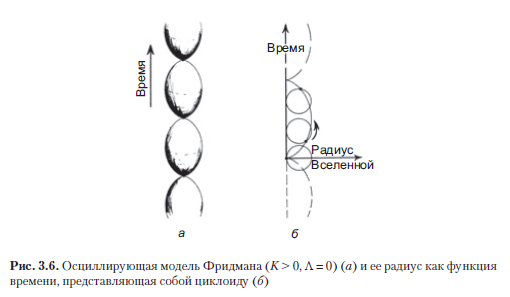
На заре релятивистской космологии модель с положительным значением K (и Λ = 0) часто именовалась осциллирующей (рис. 3.6 a), поскольку циклоидная кривая будет продолжаться бесконечно, если мы позволим «обручу» сделать более одного оборота (штриховая кривая на рис. 3.6 б). Можно предположить, что непрерывно сменяющие друг друга участки циклоиды могут соответствовать последовательным циклам в истории реальной Вселенной, где под действием некоей встряски каждое схлопывание, которое претерпевает Вселенная, сменяется новым Большим взрывом. Подобная возможность возникает также при K = 0, и можно предположить, что на более раннем этапе пространство-время претерпело коллапс, идентичный повороту времени вспять на этапе расширения, и Большое схлопывание того этапа совпадает с Большим взрывом, который мы считаем началом нынешнего расширения Вселенной. Опять же, пришлось бы вообразить себе некий отскок, который каким-то образом позволяет превратить схлопывание в расширение.
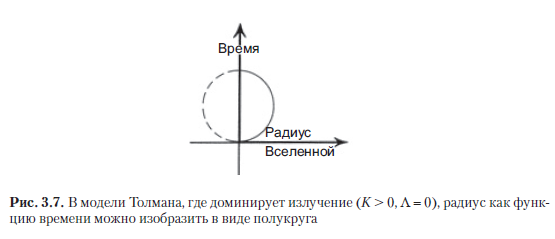
Однако чтобы такая картина стала физически правдоподобной, требуется представить некоторую убедительную математическую схему, которая бы находилась в согласии с современными физическими представлениями и методами и в которую вписывался бы такой отскок. Например, предположим, что можно изменить взятые на вооружение Фридманом уравнения состояния, при помощи которых он пытался описать общее распределение материи в его «равномерно размазанных» галактиках. Фридман пользовался приблизительной моделью, которая иногда называется пылевой; в этой модели не учитываются никакие взаимодействия (кроме гравитации) между «составными элементами» (то есть «галактиками»), мировые линии которых являются линиями времени. Если изменить уравнения состояния, это может существенно отразиться на свойствах R (t) вблизи t = 0. Еще более точной аппроксимацией, нежели пыль Фридмана (в период сразу после Большого взрыва), представляется такое уравнение состояния, которым позже пользовался Ричард Чейз Толман [1934], американский специалист по математической физике и космологии. В толмановских ФЛРУ-моделях использовалось уравнение состояния чистого излучения. Считается, что оно хорошо аппроксимирует состояние материи на самых ранних этапах развития Вселенной, когда было так жарко, что на каждую частицу приходилось значительно больше энергии, чем по уравнению 
для массы m даже наиболее тяжелых частиц, которые могли существовать сразу после Большого взрыва. В схеме Толмана для случая K > 0 кривая R (t) является не дугой циклоиды, а (при правильно подобранном масштабе R и t) образует полукруг (рис. 3.7). В случае с пылевой моделью можно было бы обосновать переход от Схлопывания к Взрыву, прибегнув к аналитическому продолжению (см. раздел A.10), которое действительно позволяет переходить от одной дуги циклоидной кривой к следующей таким математическим методом. Но в толмановской модели с чистым излучением аналитическое продолжение просто дополнило бы полукруг и превратило его в круг, а это не имеет никакого смысла, если данная процедура интересует нас для описания отскока, то есть должна допускать продолжение в сторону отрицательных значений t.
Для того чтобы новое уравнение состояния описывало механизм отскока, необходимо что-то гораздо более радикальное, чем излучение Толмана. В данном случае заслуживает внимания такой серьезный момент: если отскок происходит при некотором несингулярном переходе, в процессе которого сохраняются гладкость пространства-времени и пространственная симметрия модели, то сходящиеся временные линии фазы сжатия могут превратиться в расходящиеся временные линии фазы расширения, пройдя через «бутылочное горлышко», которое объединило бы обе эти фазы. Если бы это горлышко было гладким (несингулярным), то превращение такого экстремального схождения временных линий в экстремальное расхождение было бы достижимо при невероятной кривизне горлышка, что приводило бы к сильному отталкиванию, а это грубо противоречит стандартным условиям положительности энергии, которым удовлетворяет обычная классическая материя (см. разделы 1.11, 3.2 и 3.7; [Hawking and Penrose, 1970]).
Поэтому нельзя рассчитывать, что какое-либо разумное классическое уравнение состояния позволило бы нам описать отскок в контексте ФЛРУ-моделей, и неизбежно встает вопрос:, а не помогли бы нам продвинуться в этом направлении уравнения квантовой механики? Необходимо учитывать, что вблизи классической ФЛРУ-сингулярности кривизна пространства-времени становится неопределенно велика. Если бы мы попытались описать такую кривизну в терминах ее радиуса, то этот радиус (величина, обратная кривизне), был бы соответственно мал. Продолжая придерживаться понятий классической геометрии, мы с приближением к классической сингулярности получали бы все меньшие радиусы кривизны пространства-времени, и в итоге радиус стал бы даже меньше планковских масштабов порядка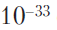 
см (см. разделы 1.1 и 1.5). Большинство теоретиков, размышляя о квантовой гравитации, предполагают, что при таких масштабах пространство-время уже резко отличалось бы от своего привычного вида (гладкое многообразие) (хотя в разделе 4.3 я выдвину совершенно иные аргументы на этот счет). Так это или нет, но нет никаких оснований сомневаться в том, что процедуры общей теории относительности неизбежно придется модифицировать, чтобы они сочетались с методами квантовой механики на подступах к такой радикально искривленной пространственно-временной геометрии. То есть нам нужна подходящая к нашему случаю теория квантовой гравитации, которая позволила бы справиться с ситуациями, в которых классические эйнштейновские процедуры приводят к сингулярности (но ср. с разделом 4.3).
Часто приходится слышать утверждения, что подобный прецедент уже был. Как отмечалось в разделе 2.1, в начале XX века возникла серьезная проблема с классическими представлениями об атоме, поскольку, согласно теории, атомы должны были катастрофически схлопываться в сингулярное состояние, когда электроны по спирали падали бы на ядро (с генерацией импульса излучения), и решить эту проблему удалось лишь с появлением квантовой механики. Не следует ли ожидать, что и при обсуждении подобного катастрофического коллапса всей Вселенной ситуация могла бы проясниться на уровне квантовой механики? Но вот загвоздка: даже сейчас не существует общепризнанной гипотезы квантовой гравитации. Еще серьезнее тот факт, что большинство из уже выдвигавшихся гипотез не решают проблему сингулярностей — сингулярности остаются даже в квантованной теории. Есть некоторые заслуживающие внимания исключения — гипотезы, связанные с несингулярным квантовым отскоком [Bojowald, 2007; Ashtekar et al., 2006], но мне придется вернуться к этой теме в разделах 3.9 и 3.11 (а также в разделе 4.3), где я утверждаю, что подобные гипотезы на самом деле не дают особых надежд на решение проблемы сингулярности именно в нашей Вселенной.
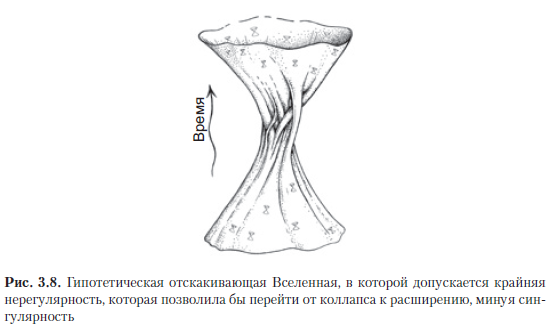
Совершенно иная возможность избежать сингулярности связана с ожиданиями, что небольшие отклонения от точной симметрии, присутствующие на этапе коллапса Вселенной, могли бы радикально расти по мере приближения Большого схлопывания, поэтому непосредственно перед полным коллапсом структура пространства-времени далеко не точно соответствовала бы ФЛРУ-модели. Поэтому часто озвучивается надежда на то, что сингулярность, которая проявляется в ФЛРУ-моделях, может быть ложной и что в более общей асимметричной ситуации такие классические пространственно-временные сингулярности просто не возникнут; следовательно, есть основания ожидать, что в общем случае коллапсирующая Вселенная ввиду некоей сложной промежуточной пространственно-временной геометрии (рис. 3.8) может перейти к нерегулярному расширению. Даже сам Эйнштейн пытался выдвигать такие аргументы — о том, что сингулярности можно избежать путем отскока от нерегулярного коллапса [Einstein, 1931; Einstein and Rosen, 1935] или потому, что конечному коллапсу и сингулярности могут как-то воспрепятствовать орбитальные движения небесных тел [Einstein, 1939].
Можно утверждать, что после такого почти сингулярного (но не строго сингулярного) коллапса возникнет состояние, возмущения которого станут постепенно разглаживаться, и в результате оно станет сильно напоминать расширяющуюся ФЛРУ-модель (как на рис. 3.8). В 1963 году эту задачу подробно проанализировали два советских физика-теоретика — Евгений Михайлович Лифшиц и Исаак Маркович Халатников [Лифшиц и Халатников, 1963]. Их работа показывает, что в обычных условиях такие сингулярности, по-видимому, не возникают, что подкрепляет описанную выше гипотезу несингулярного отскока. Соответственно, утверждалось, что в общей теории относительности пространственно-временные сингулярности, возникающие при гравитационном коллапсе и проявляющиеся в известных точных решениях коллапсирующих моделей Фридмана или других ФЛРУ-моделей, порождаются лишь потому, что известные решения обладают нереалистичными специфическими свойствами, например строгой симметрией. Поэтому такие сингулярности не сложились бы в условиях типичных асимметричных пертурбаций. Однако это предположение не подтвердилось, о чем и пойдет речь в следующем разделе.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 30% по купону — Пенроуз
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
