Нетривиальные метрики эффективности рекламных кампаний07.02.2019 15:05

При анализе цепочек рекламных каналов некоторые достаточно простые, но полезные идеи проскакивают незамеченными. Хорошо знакомые с математикой аналитики сразу стремятся погрузиться машинное обучение, а далекие от математики аналитики вообще не очень понимают, куда и как смотреть в отрыве от стандартных отчетов Google Analytics.

В то же время такая достаточно банальная вещь как распределение длин цепочек атрибуции за период может рассказать весьма красноречивые вещи, причем не только об эффективности вашей рекламы.

В данной статье я покажу, как по этому распределению:

Выделить среди переходящих по рекламным каналам тех пользователей, кто реагирует на рекламу;
Оценить эффективность влияния вашей рекламной кампании на эту группу;
Оценить как бы реагировали на ваш товар люди, если бы знали про него все, что вы хотели им сообщить;
Оценить оптимальную с точки зрения уровня конверсии частоту показа рекламных объявлений.

Группы пользовательской вовлеченности

Допустим вы имеете данные по всем цепочкам каналов, которые проходили пользователи за месяц. Для начала разобьем их на две группы:

Цепочки, которые закончились конверсией.
Цепочки, которые не закончились конверсией.

Построим таблицу, содержащую количество цепочек определенной длины:

Длина цепочки	1	2	3	4	…
Количество цепочек с конверсией	200	400	600	1000	…
Количество цепочек без конверсий	400000	300000	30000	7000	…

После этого можно построить графики зависимости логарифма количества сконвертировавашихся и несконвертировавшихся цепочек от их длины и посмотреть на них вместе. Например, вот такой график мы строили для одного своего B2C клиента за некоторый период времени:

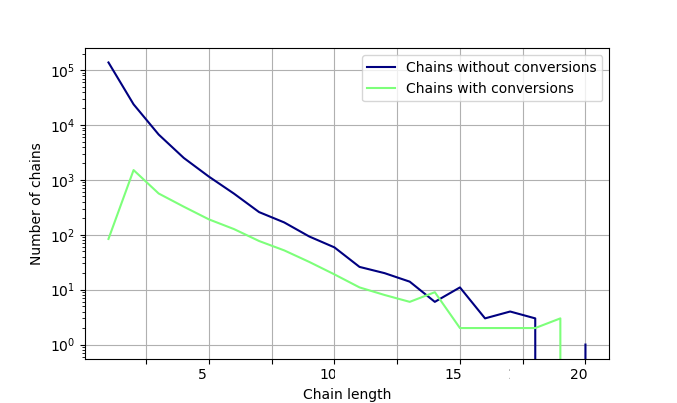
Рис. 1. Зависимость количества цепочек от длины цепочки

Каждая точка графика задает некоторую группу пользователей, которые в рассматриваемый период или совершили конверсию (зеленая линия) или не совершили (синяя линия) при этом пройдя цепочку заданной длины. Оба графика идут вниз, потому что количество цепочек уменьшается по экспоненте с ее длиной. Для коротких цепочек (от 2 до 7–8) уровень конверсии (расстояние между линиями) постепенно увеличивается.

Есть несколько крайне интересных моментов, которые можно выделить, смотря на этот график:

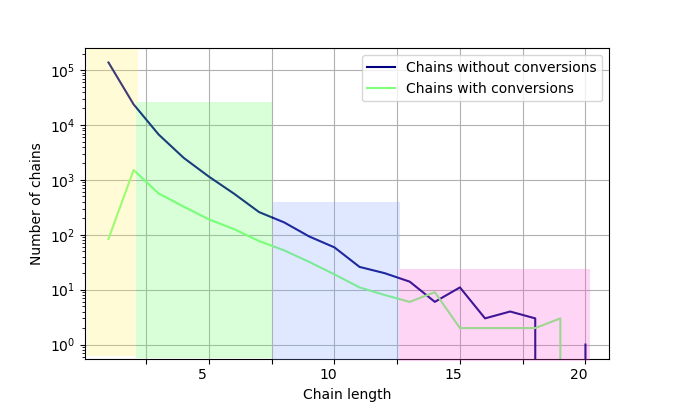
Рис. 2. Зависимость количества цепочек от их длины с наложенными регионами, выделяющими различные типы поведения.

У нас 4 явно выделенных группы пользователей:

Цепочки длины 1 и 2 (желтый). Количество конверсий растет, но сам этот рост и значения уровня конверсии (conversion rate) не соответствует главной тенденции. Это пользователи, которые только знакомятся с товаром.
Цепочки длины с 3 до 9 (зеленый). Главная тенденция, когда количество конверсий уменьшается. Графики сближаются, что говорит, что соотношение цепочек изменяется в сторону увеличения доли цепочек с конверсией. Т.е. уровень конверсии растет. Это соответствует пользователям, которые целенаправленно переходят по рекламным объявлениям.
Цепочки с 9 до 15 (синий). Количество конверсий уменьшается, а уровень конверсии остается неизменным. Графики идут параллельно, что говорит, что уровень конверсии неизменен. Пользователи имеют представление о том, каким образом организация может удовлетворить их потребности, и дополнительная реклама не увеличивает вероятность покупки.
Больше 15 (розовый). Меньше 10 конверсий и цепочек без конверсий. Слишком мало данных, чтобы что-то говорить.

Выделение этих 4 групп помогает понять объемы людей, которые потенциально реагируют на рекламу. Это по большей части группа (2).

Анализ уровня конверсии для групп

Для начала выкинем все не нужное. Длины больше 15 (в рамках этих данных) для нас не очень информативны. Слишком маленькое количество цепочек такой длины не позволяет сделать какие-то выводы. Нарисуем график зависимости уровня конверсии от длины цепочки:

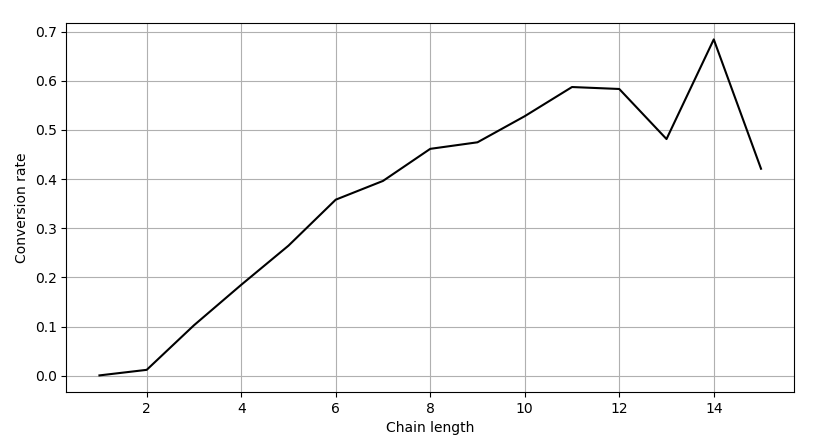
Рис. 3. Зависимость уровня конверсии от длины цепочки

Это график приближенно является сигмоидой. Такого рода зависимости описываются Логистической регрессией. Описание полученной зависимости с помощью логистической регрессии помогает сделать дополнительные полезные выводы, однако хорошему приближению с помощью логистической регрессии мешают два факта:

Нижний хвост слишком низкий, регрессия будет сильно завышать вероятность конверсии для коротких длин цепочек.
При увеличении количества цепочек график стремится не к 1, как сигмоида, а к 0.5.

Оба эти вопроса решаются достаточно просто.

Почему нижний хвост имеет такие неадекватно (для лог-регрессии) низкие вероятности?

Интуитивно очевидно, что если человек хотя бы три раза перешел по ссылкам на ваш ресурс, наверное, это не совсем случайно вышло. А случайность одного раза очень вероятна. Таким образом, поставленный вопрос решается просто и радикально — все эти люди оказались на сайте случайно (скорее всего), и им и ни ваша продукция, ни ваши сервисы не были нужны. Но вот они на вашем сайте, и появляется вероятность, что они конвертируются.

Поэтому просто не будем больше рассматривать эту группу. Для приближения логистической регрессией будем рассматривать только пользовательские группы (2) и (3).

Как избавиться от того, что вероятность стремится не к 1, если в логистических регрессиях она должна стремиться к 1?

Что дают рекламные компании? Они дают возможность клиенту полностью познакомиться с фирмой, ее сервисами и удобствами. Если человек уже узнал все про фирму, это обязательно значит, что он что-то купит? Нет. Скорее всего есть десятки и сотни альтернатив рекламируемому сервису. Человек, который знает уже все про конкретно ваш сервис, скорее всего с некоторым количеством других сервисов тоже знаком достаточно близко. И теперь он имеет достаточно информации, чтобы выбирать с какой-то вероятностью некую фирму, в которой он что-то закажет. И эта вероятность меньше 1. Увеличение количества проходов по рекламным объявлениям с некоторого количества становится бессмысленным. Поэтому, чтобы график стремился к 1, надо всего лишь разделить все значения уровней конверсий на значение вероятности к которой график стремится при увеличении количества проходов по рекламе.

Интегральные оценки эффективности организации и ее маркетинговой стратегии

Посмотрим на вышесказанное с другой стороны. Для достаточно длинных цепочек количество дополнительных проходов пользователя по рекламе уже не играет роли. Значение имеет что-то другое. Назовем это степенью удобства фирмы как таковой. Она постоянная для организации.

Тогда общая вероятность конверсии разбивается на произведение двух вероятностей:

$P_{conv}(l)=P_{marketing}(l)*P_{firm},$

где $P_{firm}$ — интегральная оценка эффективности организации, т.е. вероятность купить что-то в организации, про которую ты уже знаешь все, что можно, и осознанно выбираешь между этой организацией и альтернативами (дополнительные проходы по рекламным каналам не повлияют на решение о покупке). $P_{marketing}(l)$ — интегральная оценка эффективности маркетинговой стратегии, т.е. вероятность купить что-то в организации при условии, что только маркетинг и влияет, и если человек будет знать все, что можно, то он обязательно купить именно в этой организации, а альтернативы рассматривать не будет. И, конечно, эта вероятность зависит от длины цепочки $l$ .

Если мы еще раз вернемся к рисунку 3, то увидим, что область влияния $P_{marketing}(l)$ простирается как раз на (2) группу пользователей. Для группы (3) — $P_{marketing}(l)=1$ , а значит вероятность покупки равна $P_{firm}$ . В нашем случае в среднем $P_{firm}=0.55$ , что крайне неплохо. Эта цифра говорит, что, имея все карты на руках, человек из всех возможных альтернатив выбирает именно эту организацию в 55% случаев.

Ну и остается добавить, что теперь у нас есть рационализация для $P_{marketing}(l)$ , который стремится к 1. К нему теперь можно применить простую однофакторную логистическую регрессию. Это мы и сделаем, приблизив сигмоидой данные, нормированные на 1 путем деления данных на $P_{firm}$ .

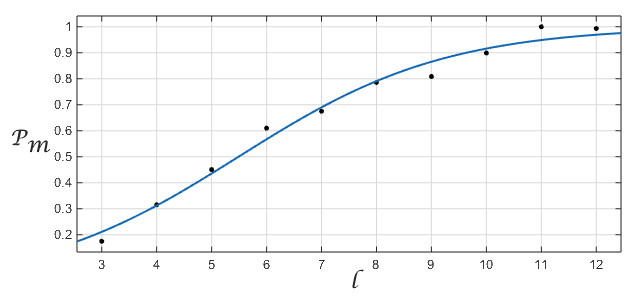
Рис. 4. Зависимость конверсии от длины цепочки с наложенной кривой для логистической регрессии.

На графике $l$ — длина цепочки, Pm— $P_{marketing}(l)$ . Показатель для экспоненты лог-регресси (log-odds ratio) = 0.53. Если бы у фирмы была бы 100% вероятность «осознанной конверсии»( $P_{firm}=1$ ), это бы примерно значило, что с каждым увеличением цепочки на один, соотношение количества цепочек с конверсией и без конверсии изменялось бы на [exp (0.53) =1.699].

Этот показатель оценивает степень эффективности маркетинговой стратегии в целом. Чем быстрее достигается вероятность $P_{firm}$ , тем эффективнее работает стратегия. Естественно, надо следить, чтобы $P_{firm}$ принимал значения, удовлетворительные для вашего бизнеса, иначе эффективная маркетинговая стратегия заставит потенциального клиента купить что-то не у вас.

Оценка оптимальной частоты показа рекламы на канале

Рассмотрим рисунок (3), где изображена зависимость вероятности конверсии от количества пройденных на данный момент пользователем каналов. Каждой точке на графике соответствует некоторый условный срез целевой аудитории. Например, люди, которые прошли 10 каналов, чем-то отличаются от тех, которые прошли только 2, потому что большинство из тех, кто прошел два канала, до 10 не дойдут.

Более того, на тех, кто прошел 10 каналов, маркетинговые программы скорее всего уже не действуют. Они уже видели всю возможную рекламу. На тех, кто прошел только два канала, реклама может быть сработает. Таким образом, вся маркетинговая стратегия должна быть сфокусирована именно на группе (2). Люди, которые прошли больше двух каналов, но еще не прошли, например, 10.

Наше исследование данных показало, что для группы (2) существует значительная отрицательная корреляция между уровнем конверсии и общим количеством переходов по рекламе за некоторый период. Т.е. чем больше людей из ЦА в принципе прошли по некоторому рекламному каналу, тем меньше вероятность, что член группы (2) этого канала сконвертируется.

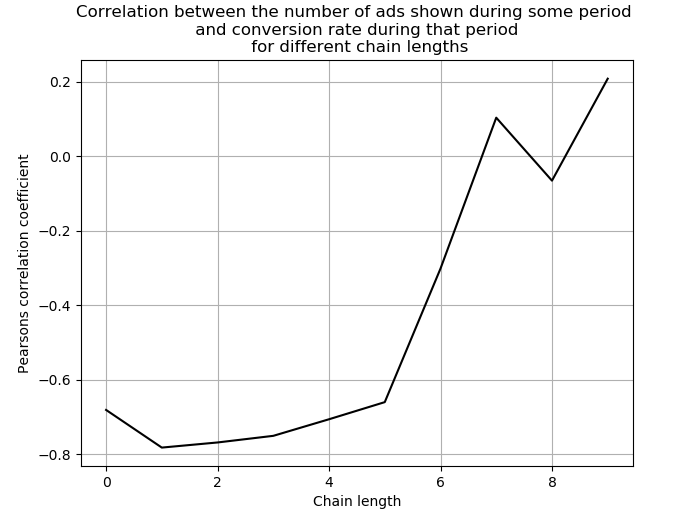
Рис. 5. Зависимость между корреляцией и разными длинами цепочек. Корреляция — это корреляционный коэффициент пирсона между уровнем конверсии и общим количеством переходов по рекламным каналам.

Это может объясняться тем, рост переходов связан с ростом показов. Интеллектуальные алгоритмы рекламных площадок пытаются показать рекламу наиболее эффективной части ЦА, но эта часть ограничена. Таким образом с увеличением количества показов алгоритмы вынуждены начать показывать рекламу менее эффективной части ЦА. У этой части ЦА меньше вероятность конверсии.

Можно предположить, что существует некоторый оптимальный выбор частоты показов рекламного объявления на канале, который бы задевал только максимально эффективную часть ЦА. Степень адекватности выбора текущей частоты можно оценить, посчитав корреляцию между общим количеством переходов за период и уровнем конверсии. Если эта корреляция отрицательная, частоту показов надо уменьшить. Если она примерно равна 0, то размер оптимален. Если она положительная, размер аудитории можно увеличить.

В нашем случае, изменение частоты показов, которое привело к снижению количества переходов на 25%, привело к повышению среднего уровня конверсии группы (2) с 3.5% до 4%.

Выводы и ограничения

Основные предложенные метрики:

Размер группы (2). Позволяет оценить, сколько людей в рассматриваемом периоде активно реагировали на рекламные объявления.
Вероятность конверсии человека, который вообще случайно проходил и ему ничего не надо от организации. Она оценивается по уровню конверсии «одношаговых» цепочек. В случае рассмотренных тут данных это 0.06%.
Разделяя вероятность конверсии в зависимости от длины цепочек на две и можно оценить:
- Интегральную оценку эффективности организации. Т.е. Вероятность купить товар при условии, что при дополнительном просмотре рекламы мнение человека о товаре и фирме совсем никак не меняется. В нашем случае это 55%.
- Интегральная оценка эффективности маркетинговой стратегии по показателю логистической регрессии, которой можно приблизить имеющуюся зависимость уровня конверсии от длины цепочки. С каждым увеличением цепочки на один вероятность конверсии увеличивается, и она достигла бы в какой-то момент 100%, если бы $P_{firm}=1$ . Показатель логистической регрессии указывает степень выраженности этого увеличения.
Корреляция между уровнем конверсии и общим количеством переходов группы (2) по рекламному каналу за период позволяет оценить оптимальную частоту показов рекламных объявлений на канале.

У всего вышесказанного есть ряд ограничений в интерпретации. И основное ограничение накладывает на нас конечное время рассмотрения. Очевидно, что достаточно длинные цепочки еще могут окончиться конверсией где-то в будущем (которое мы еще не застали) и некоторый «реальный» уровень конверсии цепочек может быть несколько выше. Разумно предполагать, что Pfirm получается несколько заниженным и данная оценка — это интегральная оценка эффективности организации снизу. Для избежания этих сложностей можно рассматривать такой временной отрезок, на котором все эти эффекты конечного времени были бы исчезающе малы. Например, целый год.

P.S. Чтобы быть в курсе новостей компании Maxilect и первыми узнавать обо всех публикациях, подписывайтесь на наши страницы в VK, FB или Telegram-канал.