Нестандартная кластеризация 5: Growing Neural Gas
Часть первая — Affinity Propagation
Часть вторая — DBSCAN
Часть третья — кластеризация временных рядов
Часть четвёртая — Self-Organizing Maps (SOM)
Часть пятая — Growing Neural Gas (GNG)
Доброго времени суток, Хабр! Сегодня я бы хотел рассказать об одном интересном, но крайне малоизвестном алгоритме для выделения кластеров нетипичной формы — расширяющемся нейронном газе (Growing Neural Gas, GNG). Особенно мало информации об этом инструменте анализа данных в рунете: статья в википедии, рассказ на Хабре о сильно изменённой версии GNG и пара статей с одним лишь перечислением шагов алгоритма — вот, пожалуй, и всё. Весьма странно, ведь мало какие анализаторы способны работать с меняющимися во времени распределениями и нормально воспринимают кластеры экзотической формы —, а это как раз сильные стороны GNG. Под катом я попробую объяснить этот алгоритм сначала человеческим языком на простом примере, а затем более строго, в подробностях. Прошу под кат, если заинтриговал.
(На картинке: нейронный газ осторожно трогает кактус)
Статья устроена следующим образом:
- Простая аналогия из жизни
- Математическая формулировка алгоритма
- Разъяснение алгоритма
- Советы по подбору гиперпараметов
- Обсуждение c примерами работы
Кроме того, в следующей статье я планирую рассказать о нескольких модификациях и расширениях нейронного газа. Если вы хотите сразу ухватиться за самую суть, можете пропустить первую секцию. Если вторая часть покажется слишком запутанной, не беспокойтесь: в третьей будут даны пояснения
Пример
Два друга-программиста Алиса и Борис решили организовать агентство скорой компьютерной помощи. Клиентов ожидается много, поэтому в рабочие часы они сидят каждый в своей машине со всем оборудованием и ждут звонков. Они не хотят платить за координационный центр, поэтому по-быстрому написали приложение для телефона, определяющее по GPS местоположение клиента, и направляющее к нему ближайшую машину (для простоты предположим, что ситуаций, когда на заказ отправляется не ближайший мастер не бывает, машина возвращается почти сразу). Также у Алисы и Бориса есть рации, чтобы общаться друг с другом. Однако у них есть лишь примерное осознание того, откуда ожидать заказов, и следовательно, только примерное понимание, на какой стоянке ожидать новых клиентов, чтобы путь до них был как можно меньше. Поэтому после каждого заказа они немного меняют своё местоположение и советуют друг другу, какую область захватить. То есть если очередной клиент возник на 5 километров севернее и 1 километр восточнее текущей стоянки Алисы, и Алиса оказалась ближайшей к нему, то после заказа она перенесёт свою стоянку на 500 метров севернее и 100 метров восточнее и посоветует Борису переместиться на 50 метров на север (и 10 метров на восток, если его не затруднит).
Дела у друзей идут в гору, но их всё ещё не устраивают затраты времени на порожний проезд до клиентов, поэтому они включают в свою компанию Василису, чтобы она взяла часть заказов из мёртвой зоны на себя. Так как Алиса с Борисом ещё не научились предсказывать наперед, откуда пойдут заказы, они предлагают Василисе занять местоположение между ними и так же подстраивать его. Василисе выдаётся рация и два старых члена команды по очереди наставляют её.
Встаёт вопрос, держать ли выделенную рацию Алиса — Борис. Они решают определиться с этим попозже. Если окажется так, что Василиса сильно сместится с линии А-Б и Алиса часто будет становиться вторым ближайшим мастером для клиентов Бориса (и наоборот), то заведут. Нет так нет.
Через некоторое время к команде присоединяется Георгий. Ему предлагают место между людьми, которым чаще всего и сильнее всего приходится менять стоянку, так как именно там больше всего накладные расходы. Позицию по умолчанию теперь пересматривают только мастер, оказавшийся ближе всего к заказу и люди, имеющие до него прямой доступ до рации: если в какой то момент в компании есть рации А-В, Б-В, Б-Г, и Борис принимает заказ, то после исполнения Борис сильно меняет местоположение, Василиса и Георгий — немного, Алиса стоит на той же стоянке, где и стояла.
Рано или поздно распределение заказов по городу начинает меняться: кое-где все возможные проблемы уже оказались залечены и предотвращены. Уже порядком разросшаяся компания не принимает каких-то специальных мер, чтобы с этим бороться, а просто продолжает следовать алгоритму подстройки стоянок. Некоторое время это работает, но в какой-то момент времени оказывается, что большинство людей в районе Василисы научились сами исправлять свои проблемы, и она никогда оказывается ни первым ближайшим мастером, ни даже вторым. Рация Василисы молчит, она простаивает и не может изменить дислокацию. Алиса и Борис думают, и предлагают ей недельку отдохнуть, после чего включиться между людьми, у которых заказов чересчур много.
Через некоторое время распределение членов агенства по городу начинает приближать распределение людей, нуждающихся в помощи.
Алгоритм
Ну ладно, теперь более строгое объяснение. Расширяющийся нейронный газ — потомок самоорганизующихся карт Кохонена, адаптивный алгоритм, направленный не на нахождение заданного фиксированного количества кластеров, а на оценку плотности распределения данных. В пространство данных специальным образом внедряются нейроны, которые в ходе работы алгоритма подстраивают местоположение. После окончания цикла оказывается, что в местах, где плотность данных высока, нейронов тоже много и они связаны друг с другом, а где мала — один-два или вовсе ни одного.
В примере выше Алиса, Борис, Василиса и Георгий играют роль нод GNG, а их клиенты — роль образцов данных.
Нейронный газ не использует гипотезу о стационарности данных. Если вместо фиксированного массива данных , у вас есть функция
, сэмплирующая данные из некоторого меняющегося со временем распределения, GNG запросто отработает и на ней. По ходу статьи для простоты я буду по умолчанию полагать, что на вход подан предзаданный
или не меняющая распределения
(и что эти случаи эквивалентны, что не совсем правда). Моменты, относящиеся к случаю меняющегося распределения рассмотрены отдельно.
Договоримся об обозначениях. Пусть — образец данных размерности
,
— матрица с положениями нейронов размера не больше чем
, где
— гиперпараметр, показывающий максимальное количество нейронов (реальный размер
может меняться в ходе работы алгоритма).
— вектор размера не больше чем
. Дополнительные гиперпараметры, влияющие на поведение алгоритма:
— скорость обучения нейрона-победителя и его соседей соответственно,
— максимальный возраст связи между нейронами,
— период между итерациями порождения новых нейронов,
— показатель затухания накопленных ошибок при создании новых нейронов,
— затухание ошибок каждую итерацию,
— количество эпох.
Алгоритм 1:
Вход:
Сколько-сколько гиперпараметров?!
В изначально 2 нейрона
и
, они связаны дугой с возрастом 0
инициализируется нулями
До сходимости выполнять:
- Сэмплировать входной вектор
- Найти два нейрона, ближайших к
. Пусть
— номер ближайшего,
— следующего за ним.
- Накопить в массиве ошибок расстояние от ноды до сгенерированного образца данных:
- Обновить местоположение
и всех нейронов, соединённых с ним рёбрами. Заметьте, что используются разные скорости обучения:
- Увеличить возраст всех дуг, исходящих из нейрона
- Если
и
уже соединены дугой, то обнулить возраст этой дуги, иначе просто создать дугу с возрастом 0 между ними
- Удалить все дуги с возрастом больше
- Удалить все ноды, из которых не исходит ни одной дуги
- Если текущая итерация делится на
без остатка и количество нод не достигло максимального значения
то
- Найти нейрон
с наибольшей накопленной ошибкой
- Среди соседей
найти нейрон
с наибольшей ошибкой
- Создать новую ноду
между
и
:
- Создать рёбра между
—
и
—
, удалить ребро
—
- Уменьшить ошибки нейронов
и
, передать новорожденному нейрону часть этих ошибок:
- Найти нейрон
- Уменьшить весь вектор ошибок:

Спокойствие, сейчас разберёмся.
Пояснения по работе алгоритма
Алгоритм выглядит немного угрожающе из-за обилия пунктов и параметров. Давайте попробуем в нём разобраться по частям.
Накопление ошибок и создание новых нейронов
Если на вход алгоритма был подан массив данных , будем считать, что каждый нейрон — «прообраз» данных, неким образом олицетворящий их. Нейроны создают в пространстве данных диаграмму Вороного и предсказывают среднее значение экземпляров данных в каждой клетке.
На картинке пример простой диаграммы Вороного: плоскость разбита на участки, соответствующие точкам внутри. Множество внутри каждого цветного многоугольника ближе к центральной точке этого полигона, чем к другим чёрным точкам.

В покрытии распределения нейронами GNG есть важное отличие: каждый участок плоскости выше имеет одинаковую «цену». Это не так в случае нейронного газа: зоны, с высокой вероятностью появления имеют больший вес:
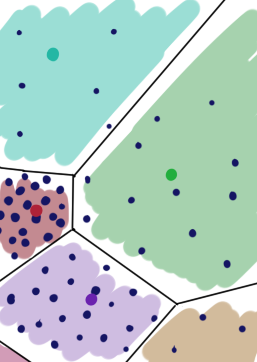
(Красный нейрон покрывает меньшую зону, потому что на ней больше экземпляров данных)
Накопленные на этапе (3) ошибки показывают, насколько нейроны хороши в этом. Если нейрон часто и сильно обновляет вес, значит либо он плохо соответствует данным, либо покрывает слишком большую часть распределения. В этом случае стоит добавить ещё один нейрон, чтобы он взял часть обновлений на себя и уменьшил глобальное несоответствие данным. Это можно сделать разными способами (почему бы просто не ткнуть его рядом с нейроном с максимальной ошибкой?), но если уж мы всё равно считаем ошибки каждого нейрона, то почему бы не применить какую-нибудь эвристику? См. (9.1), (9.2) и (9.3).
Так как данные посылаются в цикл случайным образом, ошибка — статистическая мера, но пока нейронов намного меньше, чем данных (а обычно так и есть), она довольно надёжна.
На рисунке ниже первый нейрон хорошо приближает данные, его ошибка будет возрастать медленно. Второй нейрон плохо приближает данные потому что находится далеко от них; он будет перемещаться и накапливать ошибку. Третья нода плохо приближает данные, потому что отхватила себе зону распределения, где несколько кластеров, а не один. Она не будет двигаться (в среднем), но будет накапливать ошибку, и рано или поздно породит дочернюю ноду.

Обратите внимание на пункт (9.5) алгоритма. Он уже должен быть вам понятен: новый нейрон забирает под своё крыло часть данных у собратьев и
. Как правило, мы не хотим вставлять новые ноды несколько раз в одно и то же место, так что мы уменьшаем ошибку у
и
и даём им время переместиться в новый центр. Также не забудьте про пункт (10). Во-первых, мы не хотим, чтобы ошибки возрастали бесконечно. Во-вторых, мы предпочитаем новые ошибки старым: если нода, пока путешествовала к данным накопила большую ошибку, после чего попала в место, где она хорошо приближает данные, то имеет смысл немного её разгрузить, чтобы она не делилась почём зря.
Обновление весов и рёбер
Посмотрим на этап обновления весов (4). В отличие от градиентноспусковых алгоритмов (таких как нейронные сети), которые на каждом шаге цикла обучения обновляют всё, но понемножку, нейронный газ и другие SOM-подобные техники концентрируются на масштабном обновлении весов только ближайших к нод и их прямых соседей. Это стратегия Winner Takes All (WTA, победитель получает всё). Такой подход позволяет быстро находить достаточно хорошие
даже при плохой начальной инициализации — нейроны получают большие обновления и быстро «добегают» до ближайших к ним точек данных. Кроме того, именно такой способ обновления придаёт смысл накопленным ошибкам
.
Если вы помните, как работают самоорганизующиеся карты, вы без труда поймёте, откуда растут уши у идеи соединять ноды рёбрами (6). В SOM передаётся априорная информация, как должны быть расположены друг относительно друга нейроны. У GNG таких изначальных данных нет, они ищутся на лету. Цель, отчасти, такая же — стабилизировать алгоритм, сделать распределение нейронов более гладким, но что более важно, построенная сетка сообщает нам, куда именно вставлять очередной нейрон и какие нейроны удалять. Кроме того, полученный граф связей бесценен на этапе визуализации.
Удаление нод
Теперь чуть больше об уничтожении нейронов. Как уже было упомянуто выше, добавляя ноду, мы добавляем новый «прототип» для данных. Очевидно, что нужно какое-то ограничение на их количество: хоть увеличение числа прототипов — хорошо с точки зрения соответствия данным, это плохо с точки зрения пользы от кластеризации/визуализации. Что толку от разбиения, где кластеров ровно столько, сколько точек данных? Поэтому в GNG есть несколько способов контроля их популяции. Первый, самый простой — просто жёсткое ограничение на количество нейронов (9). Рано или поздно мы перестаём добавлять ноды, и им остаётся только смещаться, чтобы уменьшить глобальную ошибку. Более мягкий, второй — удаление нейронов, которые не связаны ни с какими другими нейронами (7)-(8). Таким образом удаляются старые, отжившие своё нейроны, которые соответствуют выбросам, местам откуда «ушло» распределение или которые были порождены на первых циклах алгоритма, когда нейроны ещё плохо соответствовали данным. Чем больше нейронов, тем больше (в среднем) у каждого нейрона соседей, и тем чаще связи будут стареть и распадаться, потому что на каждом этапе цикла может быть обновлена только одно ребро (стареют, при этом, все рёбра до соседей).
Ещё раз: если нейрон плохо соответствует данным, но всё равно ближайший к ним, он двигается. Если нейрон плохо соответствует данным и есть другие нейроны, которые лучше им соответствуют, он никогда не оказывается победителем на этапе обновления весов и рано или поздно умирает.
Важный момент: хоть этого и нет в оригинальном алгоритме, я настоятельно рекомендую при работе с быстро и сильно меняющимися распределениями на шаге (5) «старить» все дуги, а не только дуги, исходящие из нейрона-победителя. Рёбра между нейронами, которые никогда не побеждают, не стареют. Они могут существовать сколь угодно долго, оставляя некрасивые хвосты. Такие нейроны легко обнаружить (достаточно хранить дату последней победы), но они плохо сказываются на работе алгоритма, истощая пул нод. Если старить все рёбра, мёртвые ноды быстро… ну, умирают. Минус: это ужесточает мягкое ограничение на количество нейронов, особенно когда их много накапливается. Маленькие кластеры могут остаться незамеченными. Также потребуется поставить больший .
Практические советы
Как уже было отмечено, благодаря стратегии WTA нейроны получают большие обновления и быстро становятся на хорошие места даже при плохих начальных положениях. Поэтому обычно не бывает особых проблем с и
— можно просто сгенерировать два случайных сэмпла
и инициализировать нейроны этими значениями. Также отмечу, что для алгоритма некритично, чтобы в него передавалось два и только два нейрона в начале: если очень хочется, можно инициализировать его какой угодно структурой, как SOM. Но по той же причине в этом довольно-таки мало смысла.
Из объяснения выше должно быть понятно, что . Слишком малое значение не оставит нейронам-родителям совсем никакого запаса в векторе ошибок, а значит ещё один нейрон они смогут породить нескоро. Это может затормозить GNG на начальных этапах. При слишком большом $\alpha$, напротив, слишком много нод может родиться в одном месте. Такое расположение нейронов потребует много дополнительных итераций цикла для подстройки. Неплохой идеей может быть оставлять
немного больше ошибки, чем
.
В посвящённой GNG научной статье советуется брать скорость обучения нейронов победителей в диапазоне . Утверждается, что
подходит для множества задач как стандартное значение. Скорость обучения соседей победителя советуют брать на один-два порядка меньше, чем
. Для
можно остановиться на
. Чем больше это значение, тем более гладким будет распределение нейронов, тем меньше будут влиять выбросы и тем охотнее нейроны будут перетягиваться на настоящие кластеры. С другой стороны, слишком большое значение
может вредить уже установившейся правильной структуре.
Очевидно, что чем больше максимальное количество нейронов , тем лучше они смогут покрыть данные. Как уже упоминалось, его не стоит делать слишком большим, так как это делает конечный результат работы алгоритма менее ценным для человека. Если
— ожидаемое количество кластеров в данных, то нижняя граница на
—
(любопытный читатель, задумайся, как из правила удаления нейронов следует утверждение «нейроны выживают парами», а из него — оценка на
). Однако, как правило, это слишком маленькое количество, ведь нужно учитывать что не всё время нейроны всё время хорошо приближают данные — должен остаться запас нейронов на промежуточные конфигурации. Мне не удалось найти исследования на тему оптимального
, но хорошим пристрелочным числом кажется
или
если ожидаются сильно вытянутые или вложенные кластеры.
Очевидно, что чем больше , тем более неохотно GNG будет избавляться от отживших нейронов. При слишком маленьком
алгоритм становится нестабильным, слишком хаотичным. При слишком большом — может потребоваться очень много эпох, чтобы нейроны переползли с места на место. В случае меняющегося во времени распределения нейронный газ в этом случае может в вовсе не достигнуть даже отдалённой синхронности с распределением. Этот параметр явно не должен быть меньше чем максимальное количество соседей у нейрона, но точное его значение определить сложно. Возьмите
и дело с концом.
Сложно дать какие-то советы по поводу . Как слишком большое так и слишком малое значение вряд ли повредят конечному результату, но эпох однозначно потребуется намного больше. Возьмите
, после чего двигайтесь методом проб и ошибок.
Насчёт количества эпох всё довольно просто — чем больше, тем лучше.
Резюмирую, что хоть у GNG и много гиперпараметров, даже с не очень точным их набором алгоритм скорее всего вернёт вам приличный результат. Просто это займёт у него гораздо больше эпох.
Обсуждение
Легко видеть, что как и SOM, Growing Neural Gas не является кластеризующим алгоритмом сам по себе; он скорее уменьшает размер входной выборки до некоторого набора типичных представителей. Получившийся массив нод можно использовать как карту датасета и сам по себе, но лучше поверх него запустить уже не раз упомянутые мной DBSCAN или Affinity Propagation. Последний особенно будет рад информации об уже имеющихся дугах между нодами. В отличие от самоорганизующихся карт, GNG хорошо внедряется и в гипершары и в гиперскладки, и умеет увеличиваться без дополнительных модификаций. Чем GNG особенно радует по сравнению со своим предком, так это тем, что не так сильно деградирует с повышением размерности датасета.
Увы, и нейронный газ не лишён недостатков. Во-первых, сугубо технические проблемы: программисту придётся потрудиться над эффективной реализацией когерентных списков нод, ошибок и дуг между нейронами со вставкой, удалением и поиском. Несложно, но подвержено багам, будьте осторожнее. Во-вторых, GNG (и другие WTA-алгоримты) расплачиваются чувствительностью к выбросам за большие обновления . В следующей статье и расскажу, как немного сгладить эту проблему. В-третьих, хоть я и упомянул про возможность пристально повглядываться в получившийся граф нейронов, это скорее удовольствие для специалиста. В отличие от карт Кохонена один лишь Growing Neural Gas затруднительно использовать для визуализации. В-четвёртых, GNG (и SOM) не очень хорошо чует кластеры более высокой плотности внутри других кластеров.
Под спойлером картинки с примерами работы алгоритма

Так и с более привычными, блямбоподобными:
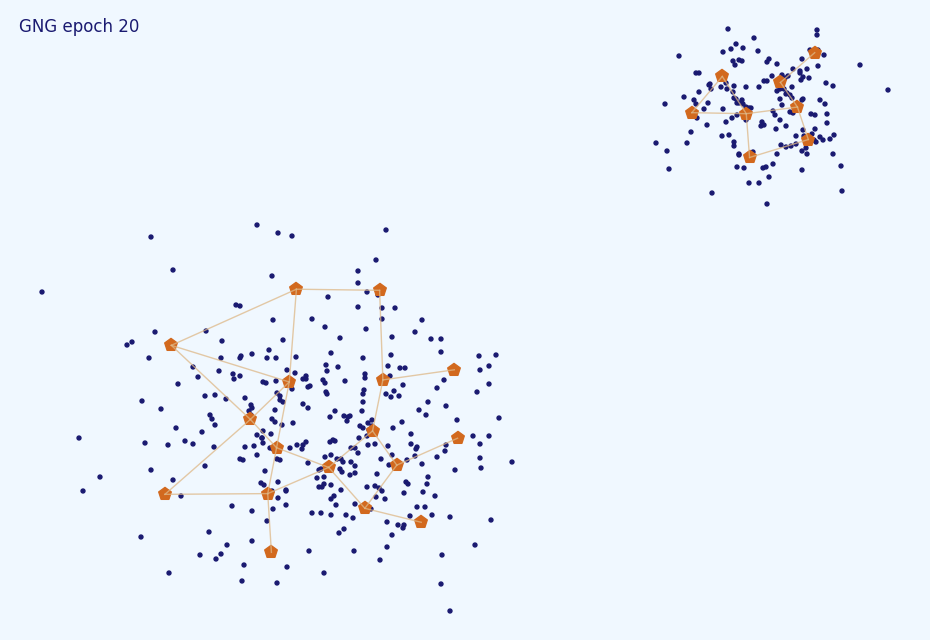

К сожалению, реализация по умолчанию чувствительна к шуму. Даже 10% выбросов здорово сбивают алгоритм с толку:

Также по одним лишь нейронам бывает сложно обнаружить скопления высокой плотности внутри других кластеров:

В простых случаях со стационарным распределением GNG не очень чувствителен к точной подстройке большинства гиперпараметров. На картинках ниже представлены результаты кластеризатора со слишком большим learning rate (0.5), слишком большим периодом рождения нейронов (1000) и слишком малым (5).
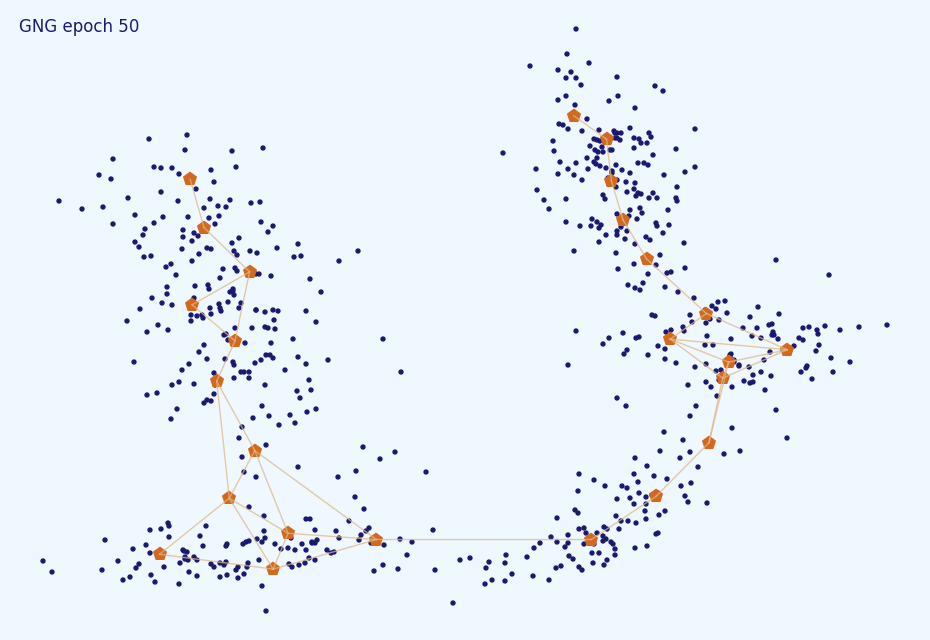

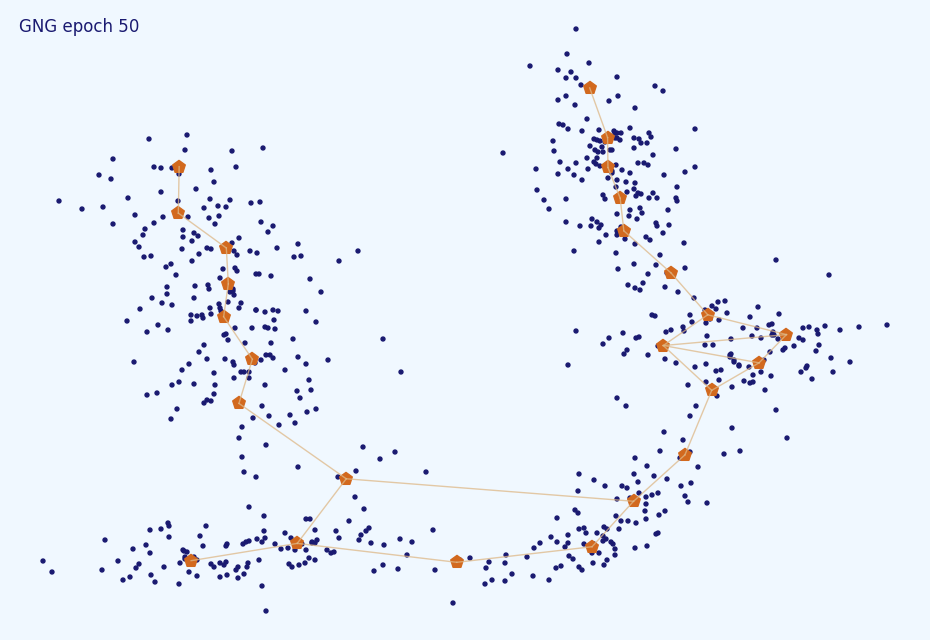
Как видите, результаты несильно отличаются от результата выше. Насчёт максимального времени жизни всё не так просто. Скорее всего повезёт ():


А может и нет. Обратите внимание на появившиеся разрывы в связях.
Чем сложнее распределение, тем больше необходимо нейронов. Но не забывайте, что плохо как слишком большое, так и слишком маленькое их количество:


А вот с динамическим распределением придётся поподбирать параметры. Причём, чем быстрее изменяется распределение, и чем оно сложнее, тем кропотливее будет работа. Пример хорошо, нормально, и плохо подобранных гиперпараметров:



Такое, как на третьей гифке бывает редко. Но даже средняя гифка довольно сильно искажает результат — обратите внимание, как нейроны переползают с места на место, образуя хвост.
Промежуточный итог
В этой статье мы рассмотрели алгоритм расширяющегося нейронного взгляда с упрощённой и с детализированной точек зрения. Мы обсудили особенности его работы и выбор гиперпараметров. Этого должно быть достаточно для самостоятельной реализации алгоритма и эффективной работы с ним. Попробуйте скачать мою простенькую версию с гитхаба и посмотреть анимации в более высоком разрешении у себя или поиграться с распределениями вот здесь. Большая часть материала статьи была почерпнута из работы Jim Holmström «Growing Neural Gas wtih Utility». В следующей статье я укажу на некоторые слабые места GNG и расскажу о модификациях, лишённые этих недостатков. Stay tuned!
