Нейропластичность в искусственных нейронных сетях
 Привет, Хабр, давно не виделись. В этом посте мне хотелось бы рассказать о таком относительно новом понятии в машинном обучении, как transfer learning. Так как я не нашел какого-либо устоявшегося перевода этого термина, то и в названии поста фигурирует хоть и другой, но близкий по смыслу термин, который как бы является биологической предпосылкой к формализации теории передачи знаний от одной модели к другой. Итак, план такой: для начала рассмотрим биологические предпосылки; после коснемся отличия transfer learning от очень похожей идеи предобучения глубокой нейронной сети;, а в конце обсудим реальную задачу семантического хеширования изображений. Для этого мы не будем скромничать и возьмем глубокую (19 слоев) сверточную нейросеть победителей конкурса imagenet 2014 года в разделе «локализация и классификация» (Visual Geometry Group, University of Oxford), сделаем ей небольшую трепанацию, извлечем часть слоев и используем их в своих целях. Поехали.Для начала рассмотрим определение. Нейропластичность — это свойство мозга изменяться под воздействием опыта или после травмы. Изменения включают в себя как создание синаптических связей, так и создание новых нейронов. Еще относительно недавно, до 70-х годов ХХ века, считалось, что часть мозга, в частности неокортекс (а это как раз вся моторика, речь, мышление и т.д.), оставалась статичной после определенного периода взросления, корректироваться могли лишь только силы связей между нейронами. Но позже более тщательные исследования подтвердили наличие нейропластичности мозга в целом. Предлагаю взглянуть на небольшое видео:[embedded content]
Привет, Хабр, давно не виделись. В этом посте мне хотелось бы рассказать о таком относительно новом понятии в машинном обучении, как transfer learning. Так как я не нашел какого-либо устоявшегося перевода этого термина, то и в названии поста фигурирует хоть и другой, но близкий по смыслу термин, который как бы является биологической предпосылкой к формализации теории передачи знаний от одной модели к другой. Итак, план такой: для начала рассмотрим биологические предпосылки; после коснемся отличия transfer learning от очень похожей идеи предобучения глубокой нейронной сети;, а в конце обсудим реальную задачу семантического хеширования изображений. Для этого мы не будем скромничать и возьмем глубокую (19 слоев) сверточную нейросеть победителей конкурса imagenet 2014 года в разделе «локализация и классификация» (Visual Geometry Group, University of Oxford), сделаем ей небольшую трепанацию, извлечем часть слоев и используем их в своих целях. Поехали.Для начала рассмотрим определение. Нейропластичность — это свойство мозга изменяться под воздействием опыта или после травмы. Изменения включают в себя как создание синаптических связей, так и создание новых нейронов. Еще относительно недавно, до 70-х годов ХХ века, считалось, что часть мозга, в частности неокортекс (а это как раз вся моторика, речь, мышление и т.д.), оставалась статичной после определенного периода взросления, корректироваться могли лишь только силы связей между нейронами. Но позже более тщательные исследования подтвердили наличие нейропластичности мозга в целом. Предлагаю взглянуть на небольшое видео:[embedded content]
Чтобы действительно ощутить всю мощь нашего мозга, давайте взглянем на эксперимент нейрофизиолога Paul Bach-y-Rita, работы которого в значительной степени повлияли на признание нейропластичности научной общественностью. Важным фактором, влияющим на мотивацию ученого, являлось то, что его отец был парализован. Совместными усилиями с братом-физиком они смогли поднять отца на ноги к 68 годам, что позволило тому даже заниматься экстремальными видами спорта. Их история показала, что даже в позднем возрасте мозг человека способен к реабилитации. Но это совсем другая история, вернемся к опыту 1969 года. Цель была серьезная: дать слепым (даже от рождения) людям возможность видеть. Для этого было взято стоматологическое кресло и переоборудовано следующим образом: рядом с креслу поставили телевизионную камеру, а к креслу подвели манипулятор, который позволял изменять масштаб и положение камеры. В спинку кресла было вмонтировано 400 стимуляторов, которые образовывали сетку: изображение, поступавшее с камеры, сжималось до размера 20 на 20; стимуляторы располагались на расстоянии 12 мм друг от друга. К каждому стимулятору был прикреплен небольшой миллиметровый наконечник, который вибрировал пропорционально току, подаваемому на соленоид, расположенный внутри стимулятора.

С помощью осциллографа можно было визуализировать изображение, создаваемое вибрацией стимуляторов.

Годом позже Пол разработал мобильную версию своей системы:
мобильный визор 1970-ого года
Человек похож на Мавроди, но это не он.
В наше время вместо тактильной передачи сигнала используют «короткий» путь через более чувствительный орган — язык. Как пишут в статьях, достаточно нескольких часов, чтобы начать воспринимать изображение рецепторами языка.Так как же это работает? Говоря на простом языке (не биологов и нейрофизиологов, а скорее на языке анализа данных), нейроны обучаются эффективно извлекать признаки и делать выводы на них. Подменяя привычный сигнал на некоторый другой, наша нейронная сеть все равно извлекает хорошие низкоуровневые признаки (на примере компьютерного зрения, приводимого ниже, это будут различные градиентные переходы или паттерны) на слоях, которые расположены близко к сенсору (глазу, языку, уху и т.д.). Более глубокие слои пытаются извлечь высокоуровневые признаки (колесо, окно). И вероятно, если искать в звуковом сигнале колесо от машины, скорее всего мы его не найдем. К сожалению, посмотреть, какие признаки извлекают нейроны, у нас не очень получится, но благодаря статье «Visualizing and Understanding Convolutional Networks» есть возможность взглянуть на низкоуровневые и высокоуровневые признаки, извлекаемые глубокой сверточной нейронной сетью. Это, конечно, не биологическая сеть, и возможно, все в реальности не так. Как минимум, это дает некое интуитивное понимание причин того, что видеть можно даже рецепторами языка.На большой картинке в спойлере изображено по несколько признаков каждого сверточного слоя и части оригинальных изображений, которые их активируют. Как вы можете заметить, чем глубже, тем менее абстрактными становятся признаки.
Visualization of features in a fully trained model
Каждый серый квадрат соответствует визуализации фильтра (который применяется для свертки) или весов одного нейрона, а каждая цветная картинка — это та часть оригинального изображения, которая активирует соответствующий нейрон. Для наглядности нейроны внутри одного слоя сгруппированы в тематические группы.
Можно предположить, что, подменяя сенсоры, нашему мозгу не нужно полностью переучивать все нейроны, достаточно переобучить только те, что извлекают высокоуровневые признаки, —, а остальные и так уже умеют извлекать качественные фичи. Практика показывает, что так оно примерно и есть. Маловероятно, что за пару часов хождения с пластиной на языке мозг успевает удалить и затем вырастить новые синаптические связи, при этом не потеряв возможность чувствовать вкус еды рецепторами языка.А теперь давайте вспомним, с чего начиналась история искусственных нейронных сетей. В 1949 году Дональд Хебб публикует книгу The Organization of Behavior, в которой описывает первые принципы обучений ИНС. Стоит заметить, что современные алгоритмы обучения недалеко ушли от этих принципов.
если рядом стоящие нейроны активируются синхронно, то связь между ними усиливается;
если рядом стоящие нейроны активируются асинхронно, то связь между ними ослабевает (на самом деле, этого правила не было у Хебба, его дописали как дополнение уже позже).
Через девять лет Френк Розенблатт создает первую модель для обучения с учителем — персептрон. Автор первой искусственной нейронной сети не преследовал цели создать универсальный аппроксиматор. Он был нейрофизиологом, и его задачей было создать устройство, которое сможет обучаться наподобие человека. Только взгляните на то, что журналисты пишут про персептрон. Имхо, это прелестно: New York Time, July 8, 1958
 …
… В персептроне были реализованы правила обучения Хебба. Как мы видим, синаптическая пластичность в правилах уже учтена в какой-то степени. И в принципе, online learning дает нам некоторую пластичность — нейросеть может постоянно дообучаться на непрерывном потоке данных, а ее прогнозы в связи с этим будут со временем меняться, постоянно учитывая изменения в данных. Но нет никаких рекомендаций по другим аспектам нейропластичности, таким как сенсорная заменяемость или нейрогенез. Но это и неудивительно, до принятия нейропластичности еще остается чуть более 20 лет. Учитывая последующую историю ИНС, ученым было не до имитации нейропластичности, вопрос был о выживаемости теории в принципе. Только после очередного ренессанса нейросетей в двухтысячных годах, благодаря таким людям, как Хинтон, ЛеКун, Бенджио и Шмидтхубер, у других ученых появилась возможность всесторонне подойти к машинному обучению и прийти к понятию transfer learning.
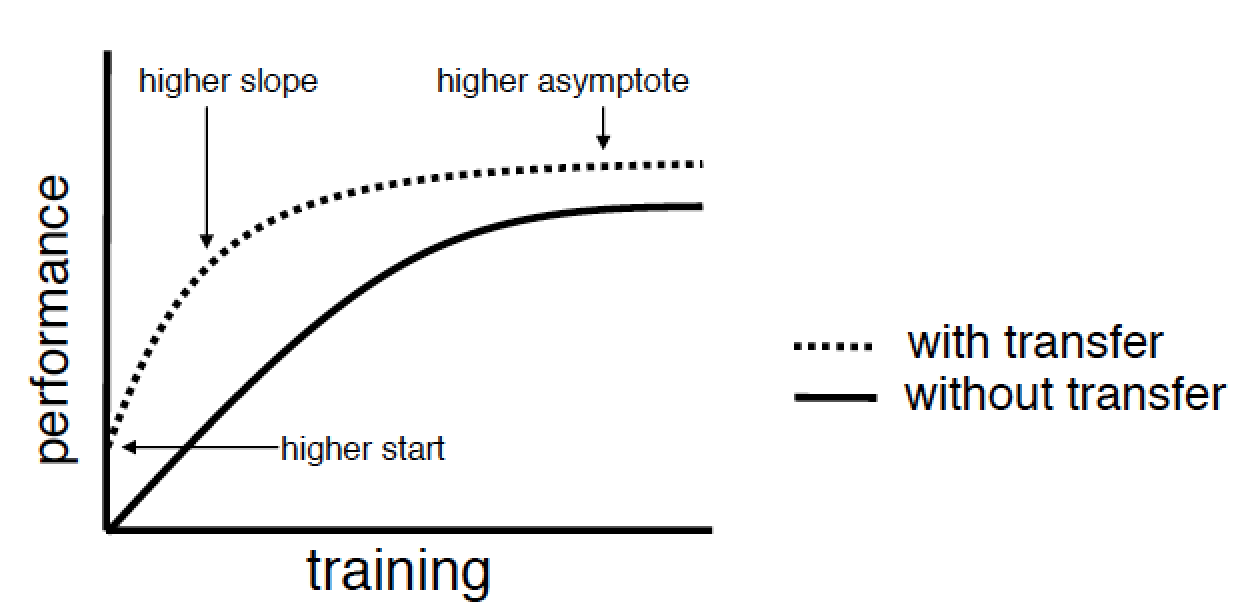
Определим цели transfer learning. Авторы публикации 2009 года с одноименным названием выделяют три основные цели: higher start — улучшение качества обучения уже на начальных итерациях за счет более тщательной подборки начальных параметров модели или какой-либо другой априорной информации;
higher slope — ускорение сходимости алгоритма обучения;
higher asymptote — улучшение верхней достижимой границы качества.
В персептроне были реализованы правила обучения Хебба. Как мы видим, синаптическая пластичность в правилах уже учтена в какой-то степени. И в принципе, online learning дает нам некоторую пластичность — нейросеть может постоянно дообучаться на непрерывном потоке данных, а ее прогнозы в связи с этим будут со временем меняться, постоянно учитывая изменения в данных. Но нет никаких рекомендаций по другим аспектам нейропластичности, таким как сенсорная заменяемость или нейрогенез. Но это и неудивительно, до принятия нейропластичности еще остается чуть более 20 лет. Учитывая последующую историю ИНС, ученым было не до имитации нейропластичности, вопрос был о выживаемости теории в принципе. Только после очередного ренессанса нейросетей в двухтысячных годах, благодаря таким людям, как Хинтон, ЛеКун, Бенджио и Шмидтхубер, у других ученых появилась возможность всесторонне подойти к машинному обучению и прийти к понятию transfer learning.
Определим цели transfer learning. Авторы публикации 2009 года с одноименным названием выделяют три основные цели: higher start — улучшение качества обучения уже на начальных итерациях за счет более тщательной подборки начальных параметров модели или какой-либо другой априорной информации;
higher slope — ускорение сходимости алгоритма обучения;
higher asymptote — улучшение верхней достижимой границы качества.
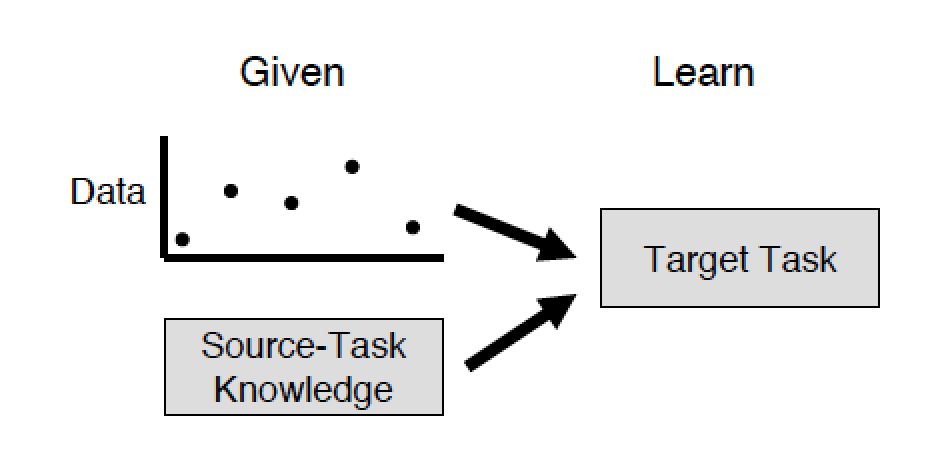
 Если вы знакомы с предобучением глубоких сетей с помощью автоенкодеров или ограниченных машин Больцмана, то вы сразу подумаете: «Так вот оно, я уже, оказывается, практиковал transfer learning или, как минимум, знаю, как это сделать». А вот, оказывается, нет. Авторы проводят четкую границу между стандартным машинным обучением и transfer learning. В стандартном подходе у вас есть только цель и набор данных, а задача заключается в том, чтобы какими-либо методами достичь этой цели. В рамках решения задачи вы можете построить глубокую сеть, предобучить ее жадным алгоритмом, построить еще с десяток таких же и каким-либо образом сделать ансамбль из них. Но все это будет в рамках решения какой-то одной проблемы, и время, потраченное на решение такой проблемы, будет сравнимо с суммарным временем, потраченным на обучение каждой модели, и ее предобучение.
Если вы знакомы с предобучением глубоких сетей с помощью автоенкодеров или ограниченных машин Больцмана, то вы сразу подумаете: «Так вот оно, я уже, оказывается, практиковал transfer learning или, как минимум, знаю, как это сделать». А вот, оказывается, нет. Авторы проводят четкую границу между стандартным машинным обучением и transfer learning. В стандартном подходе у вас есть только цель и набор данных, а задача заключается в том, чтобы какими-либо методами достичь этой цели. В рамках решения задачи вы можете построить глубокую сеть, предобучить ее жадным алгоритмом, построить еще с десяток таких же и каким-либо образом сделать ансамбль из них. Но все это будет в рамках решения какой-то одной проблемы, и время, потраченное на решение такой проблемы, будет сравнимо с суммарным временем, потраченным на обучение каждой модели, и ее предобучение.
А теперь представьте, что есть две задачи, и решали их, возможно, даже разные люди. Один из них использует часть модели другого (source task) для уменьшения временных затрат на создание модели с нуля и улучшения производительности своей модели (target task). Процесс передачи знаний от одной проблемы к другой и есть transfer learning. А наш мозг, вероятно, так и поступает. Как в примере выше, его реальная задача почувствовать вкус рецепторами языка и видеть глазами. Встает задача — воспринимать визуальную информацию рецепторами языка. И вместо того, чтобы вырастить новые нейроны или же сбросить веса старых и обучить их заново, мозг просто слегка корректирует имеющуюся нейронную сеть для достижения результата.
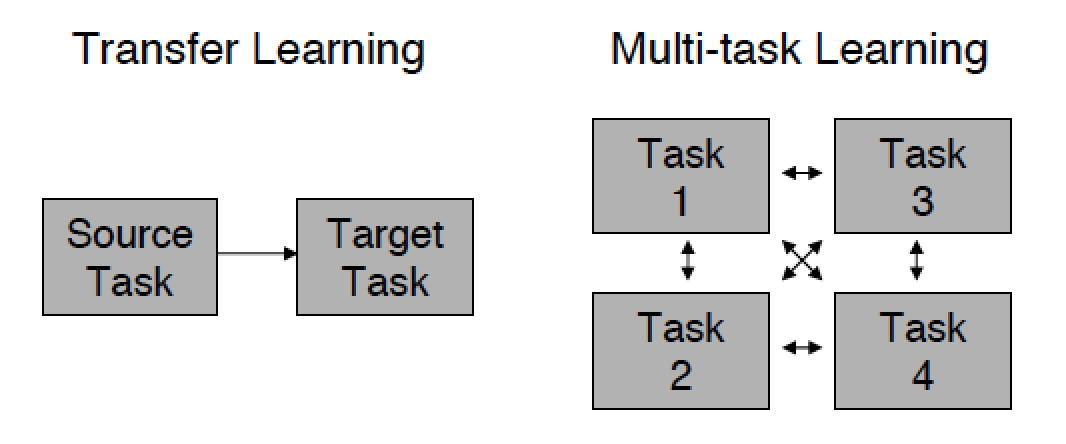
Другой особенностью transfer learning является то, что информация может передаваться только из старой модели в сторону новой, ведь старая задача уже давно решена. В то время как при стандартном подходе разные модели, участвующие в решении задачи, могут обмениваться информацией друг с другом.
Этот пост касается только той части transfer learning, которая относится к задаче обучения с учителем, но интересующимся рекомендую почитать оригинал. Оттуда вы узнаете, что, скажем, в обучении с подкреплением или при обучении байесовых сетей transfer learning стал использоваться раньше, чем в нейронных сетях.
Итак, обучение с учителем является обучением на размеченных примерах, в то время как сам процесс обучения на примерах иногда называется индуктивным обучением (переход от частного к общему), а обобщающая способность называется inductive bias. Отсюда и второе название transfer learning — inductive transfer. Тогда можно сказать, что задача трансфера знаний в индуктивном обучении — позволить знаниям, накопленным в процессе обучения старой модели, повлиять на обобщающую способность новой модели (даже при решении другой задачи).
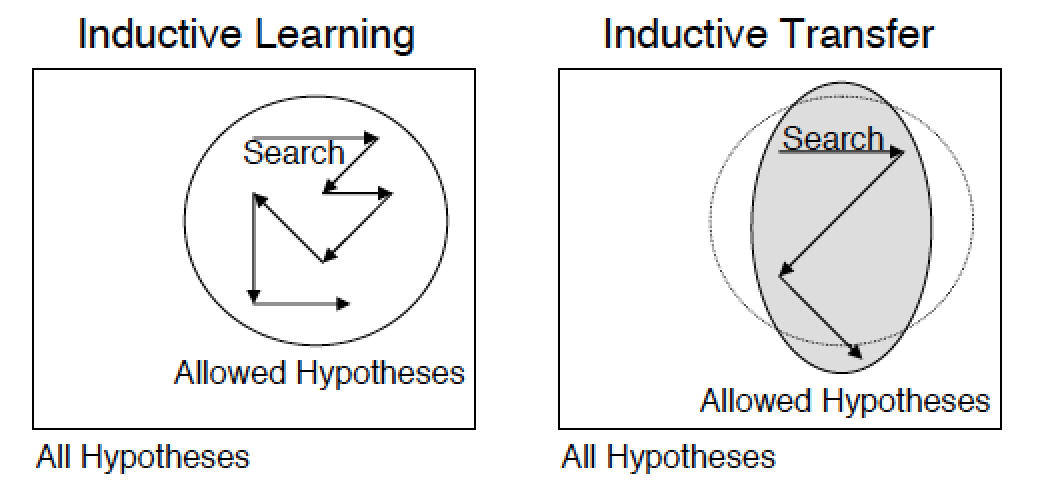
Трансфер знаний можно также рассматривать как некоторую регуляризацию, которая ограничивает пространство поиска до определенного набора допустимых и хороших гипотез.
Надеюсь, к этому моменту вы прониклись таким, на первый взгляд, ничем не примечательным подходом, как трансфер знаний. Ведь можно просто сказать, что никакой это не трансфер знаний, нейропластичность притянута за уши, а лучшее название для этого метода — копипаст. Тогда вы просто прагматик. Это, конечно, тоже неплохо, и тогда хотя бы третий раздел вам понравится. Давайте попробуем повторить нечто подобное описанному в первом разделе, но на искусственной нейронной сети.Для начала сформулируем проблему. Допустим, у вас есть очень большой набор изображений. Необходимо организовать поиск похожих изображений. Тут возникает две проблемы. Во-первых, мера схожести между изображениями неочевидна, и если просто брать евклидово расстояние от n*m-мерного вектора, результат получится не очень удовлетворительным. Во-вторых, даже если есть качественная мера, то она не позволит нам избежать полного сканирования базы, а база может содержать миллиарды изображений.
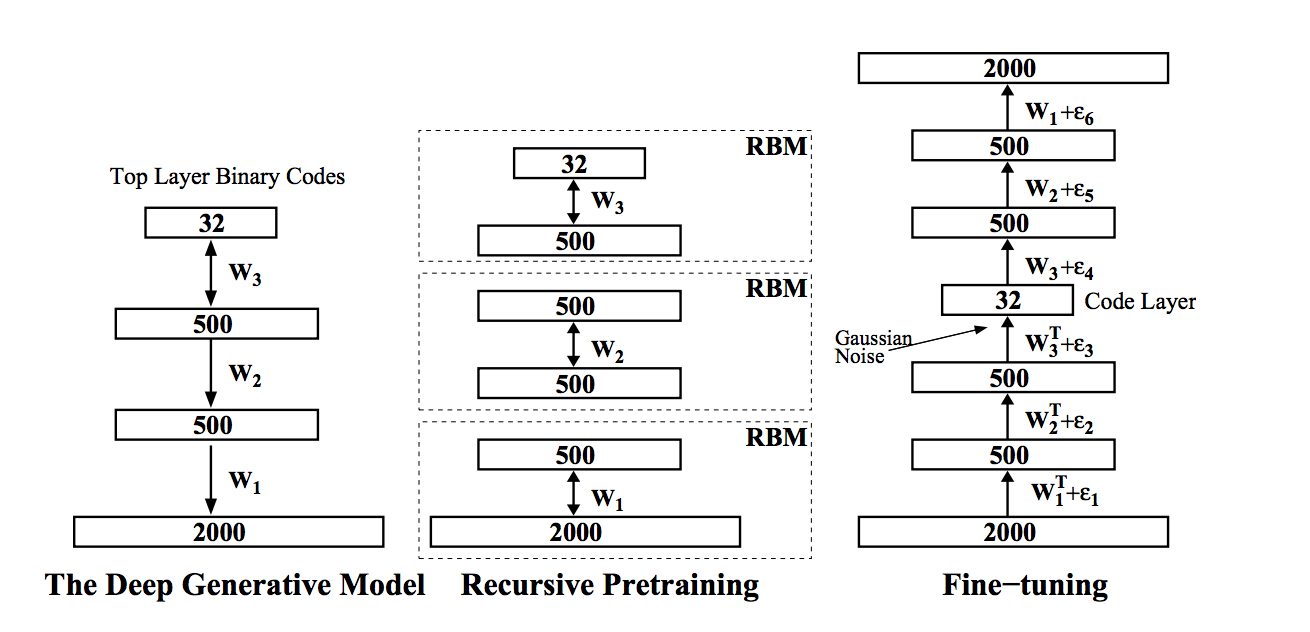
Для решения этой задачи можно использовать семантическое хеширование, один из таких способов описан у Салакхудинова и Хинтона в статье Semantic Hashing. Их идея заключается в том, что исходный вектор данных кодируется бинарным вектором малой размерности (в нашем случае это изображение, а в оригинальной статье это бинарный вектор bag of words). При таком кодировании можно осуществлять поиск похожих изображений за линейное от длины кода время, используя расстояние Хэмминга. Такое кодирование называется семантическим, так как близкие по смыслу и содержанию изображения (тексты, музыка и т.д.) в новом пространстве признаков располагаются близко друг к другу. Для реализации этой идеи они использовали глубокую сеть доверия, алгоритм обучения которой был разработан Хинтоном и компанией еще в 2006 году:
сеть на вход принимает в общем случае действительные значения (gaussian-bernoulli rbm) и кодирует их в длинный бинарный вектор, каждый следующий слой старается уменьшить длину бинарного кода (berboulli-bernoulli rbm);
такая сеть предобучается последовательно снизу вверх своей собственной ограниченной машиной Больцмана, где каждая следующая использует выход предыдущей в качестве своих входных данных;
затем сеть разворачивается в обратном порядке и обучается как глубокий автоенкодер, которому на вход подается немного зашумленный вектор, и он пытается восстановить оригинальный не зашумленный образ; этот шаг называется fine turning;
в конце концов, бинарный образ в середине автоенкодера будет искомым бинарным хэшем от входного образа.
 Мне кажется, что это гениальная модель, и я решил, что в принципе задача решена, спасибо Хинтону. Я запустил предобучение на NVIDIA Tesla K20, подождал пару дней, и оказалось, что все не так радужно, как описывает Хинтон. То ли из-за того, что картинки большого размера, то ли потому, что я использовал gaussian-bernoulli rbm, а в статье используется poisson-bernoulli rbm, то ли из-за специфичности данных, а может быть, вообще, я мало обучал. Но дальше ждать мне как-то не хотелось. И тут я вспомнил совет Максима Милакова — юзай сверточные сети, а также термин transfer learning из одной его презентации. Были, конечно, и другие варианты, начиная от сжатия размерности картинок и квантификации цветов, до классических признаков компьютерного зрения и объединения их в bag of visual words. Но раз вступив на тропу глубокого обучения, не так-то просто с нее свернуть, да и бонусы, которые обещает transfer learning (особенно экономия времени), меня прельстили.
Мне кажется, что это гениальная модель, и я решил, что в принципе задача решена, спасибо Хинтону. Я запустил предобучение на NVIDIA Tesla K20, подождал пару дней, и оказалось, что все не так радужно, как описывает Хинтон. То ли из-за того, что картинки большого размера, то ли потому, что я использовал gaussian-bernoulli rbm, а в статье используется poisson-bernoulli rbm, то ли из-за специфичности данных, а может быть, вообще, я мало обучал. Но дальше ждать мне как-то не хотелось. И тут я вспомнил совет Максима Милакова — юзай сверточные сети, а также термин transfer learning из одной его презентации. Были, конечно, и другие варианты, начиная от сжатия размерности картинок и квантификации цветов, до классических признаков компьютерного зрения и объединения их в bag of visual words. Но раз вступив на тропу глубокого обучения, не так-то просто с нее свернуть, да и бонусы, которые обещает transfer learning (особенно экономия времени), меня прельстили.
Оказалось, что упомянутая в начале группа VGG, которая победила в 2014 году в конкурсе ImageNet, выложила свою натренированную нейросеть в свободный доступ для некоммерческого использования, так что чисто в исследовательских целях я ее и скачал.
Вообще, ImageNet — это не только конкурс, но и база изображений, которая содержит в себе немногим более одного миллиона реальных изображений. Каждое изображение отнесено к одному из 1000 классов. Набор сбалансирован по классам, то есть чуть более 1000 изображений на один класс. Парни из Оксфорда выиграли в номинации локализация и классификация. Так как объектов на изображениях может быть более одного, то и оценивание происходит по тому, находится ли правильный ответ в топ-5 наиболее вероятных вариантов по версии модели. На изображении ниже вы можете увидеть пример работы одной из моделей на картинках из imagenet. Обратите внимание на забавную ошибку с далматинцем, модель, к сожалению, не нашла там вишню.

При такой вариативности датасета логично предположить, что где-то в сети присутствует эффективный извлекатель признаков, а также классификатор, который и решает, к какому классу относится изображение. Хотелось бы достать этот самый извлекатель, отделить его от классификатора и поиспользовать его для обучения глубокого автоенкодера из статьи о семантическом хешировании.
Нейросеть VGG обучена и сохранена в формате Caffe. Очень крутая библиотека для глубокого обучения, а главное — легкая в освоении, рекомендую ознакомиться. Прежде чем трепанировать сеть VGG, используя caffe, предлагаю мельком ознакомиться с самой сетью. Если интересны подробности, то рекомендую оригинальную статью — Very Deep Convolutional Networks for Large-Scale Image Recognition (название уже как бы намекает на глубину сети). А тем, кто вообще не знаком со сверточными сетями, необходимо как минимум почитать русскую википедию, прежде чем двигаться дальше, это не займет более 5–10 минут (или же есть небольшое описание на Хабре).
Итак, для статьи и конкурса авторы натренировали несколько моделей:
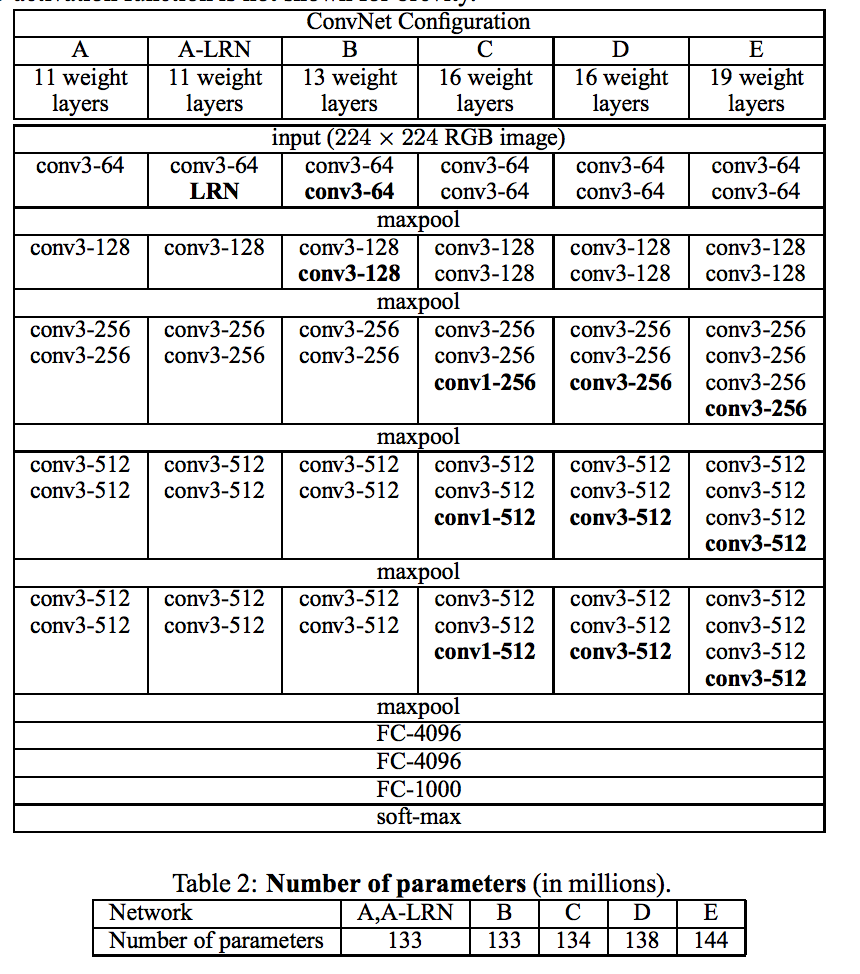
На своей странице они выложили варианты D и E. Мы для эксперимента возьмем 19-слойный вариант E, в котором первые 16 слоев сверточные, а последние три — полносвязные. Последние три слоя чувствительны к размеру изображений, так что для эксперимента, недолго думая, я выкинул их и оставил первые 16 слоев, посчитав, что высокоуровневые признаки я удалил.
В библиотеке caffe для описание моделей используется гугловский Protocol Buffers, и полное описание сети выглядит следующим образом.
19-layer model name: «VGG_ILSVRC_19_layers» input: «data» input_dim: 10 input_dim: 3 input_dim: 224 input_dim: 224 layers { bottom: «data» top: «conv1_1» name: «conv1_1» type: CONVOLUTION convolution_param { num_output: 64 pad: 1 kernel_size: 3 } } layers { bottom: «conv1_1» top: «conv1_1» name: «relu1_1» type: RELU } layers { bottom: «conv1_1» top: «conv1_2» name: «conv1_2» type: CONVOLUTION convolution_param { num_output: 64 pad: 1 kernel_size: 3 } } layers { bottom: «conv1_2» top: «conv1_2» name: «relu1_2» type: RELU } layers { bottom: «conv1_2» top: «pool1» name: «pool1» type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: «pool1» top: «conv2_1» name: «conv2_1» type: CONVOLUTION convolution_param { num_output: 128 pad: 1 kernel_size: 3 } } layers { bottom: «conv2_1» top: «conv2_1» name: «relu2_1» type: RELU } layers { bottom: «conv2_1» top: «conv2_2» name: «conv2_2» type: CONVOLUTION convolution_param { num_output: 128 pad: 1 kernel_size: 3 } } layers { bottom: «conv2_2» top: «conv2_2» name: «relu2_2» type: RELU } layers { bottom: «conv2_2» top: «pool2» name: «pool2» type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: «pool2» top: «conv3_1» name: «conv3_1» type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: «conv3_1» top: «conv3_1» name: «relu3_1» type: RELU } layers { bottom: «conv3_1» top: «conv3_2» name: «conv3_2» type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: «conv3_2» top: «conv3_2» name: «relu3_2» type: RELU } layers { bottom: «conv3_2» top: «conv3_3» name: «conv3_3» type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: «conv3_3» top: «conv3_3» name: «relu3_3» type: RELU } layers { bottom: «conv3_3» top: «conv3_4» name: «conv3_4» type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: «conv3_4» top: «conv3_4» name: «relu3_4» type: RELU } layers { bottom: «conv3_4» top: «pool3» name: «pool3» type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: «pool3» top: «conv4_1» name: «conv4_1» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv4_1» top: «conv4_1» name: «relu4_1» type: RELU } layers { bottom: «conv4_1» top: «conv4_2» name: «conv4_2» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv4_2» top: «conv4_2» name: «relu4_2» type: RELU } layers { bottom: «conv4_2» top: «conv4_3» name: «conv4_3» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv4_3» top: «conv4_3» name: «relu4_3» type: RELU } layers { bottom: «conv4_3» top: «conv4_4» name: «conv4_4» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv4_4» top: «conv4_4» name: «relu4_4» type: RELU } layers { bottom: «conv4_4» top: «pool4» name: «pool4» type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: «pool4» top: «conv5_1» name: «conv5_1» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv5_1» top: «conv5_1» name: «relu5_1» type: RELU } layers { bottom: «conv5_1» top: «conv5_2» name: «conv5_2» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv5_2» top: «conv5_2» name: «relu5_2» type: RELU } layers { bottom: «conv5_2» top: «conv5_3» name: «conv5_3» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv5_3» top: «conv5_3» name: «relu5_3» type: RELU } layers { bottom: «conv5_3» top: «conv5_4» name: «conv5_4» type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: «conv5_4» top: «conv5_4» name: «relu5_4» type: RELU } layers { bottom: «conv5_4» top: «pool5» name: «pool5» type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: «pool5» top: «fc6» name: «fc6» type: INNER_PRODUCT inner_product_param { num_output: 4096 } } layers { bottom: «fc6» top: «fc6» name: «relu6» type: RELU } layers { bottom: «fc6» top: «fc6» name: «drop6» type: DROPOUT dropout_param { dropout_ratio: 0.5 } } layers { bottom: «fc6» top: «fc7» name: «fc7» type: INNER_PRODUCT inner_product_param { num_output: 4096 } } layers { bottom: «fc7» top: «fc7» name: «relu7» type: RELU } layers { bottom: «fc7» top: «fc7» name: «drop7» type: DROPOUT dropout_param { dropout_ratio: 0.5 } } layers { bottom: «fc7» top: «fc8» name: «fc8» type: INNER_PRODUCT inner_product_param { num_output: 1000 } } layers { bottom: «fc8» top: «prob» name: «prob» type: SOFTMAX } Для того чтобы сделать описанную трепанацию, достаточно в описании модели удалить все слои, начиная от fc6 (full connected слой). Но стоит заметить, что тогда выход сети будет неограничен сверху, т.к. функцией активации является rectified linear unit:
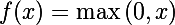
Такой вопрос удобно решается взятием сигмойда от выхода сети. Мы можем надеяться, что многие нейроны будут либо 0, либо какое-либо большое число. Тогда после взятия сигмоида у нас получится много единиц и 0.5 (сигмоид от 0 равен 0.5). Если нормировать полученные значения в промежуток от 0 до 1, то их можно интерпретировать как вероятности активации нейронов, и почти все из них будут в районе нуля либо единицы. Вероятность активации нейрона трактуется как вероятность наличия признака на изображении (например, есть ли на нем человеческий глаз).
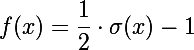
Вот типичный ответ такой сети в моем случае:
нормированный сигмоид от последнего сверточного слоя 0.00.00.00.00.00.01.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.9949340.00.00.9990470.8292190.00.00.00.00.00.00.00.00.00.00.00.9972550.00.00.00.00.00.00.01.01.00.00.9993820.00.00.00.00.9887620.00.01.01.00.01.01.00.01.01.01.01.01.00.01.01.00.00.01.01.00.01.01.00.00.00.00.00.00.8478860.00.00.00.00.9573790.00.00.00.00.01.00.9999980.00.00.00.00.00.00.00.00.00.00.00.00.00.00.00.01.00.9999990.00.548140.7397350.00.00.00.9121790.00.00.789840.00.00.00.00.00.00.00.6817760.00.00.9915010.00.9999990.9991520.00.01.00.00.00.00.00.9999961.00.01.01.00.00.8805880.00.00.00.00.00.00.8367560.9955150.00.9993540.01.01.00.01.01.00.00.9998970.00.9531260.00.00.9998570.00.00.9376950.9999831.00.00.00.00.00.01.00.00.00.0
В caffe такой вопрос решается следующим образом:
layers { bottom: «pool5» top: «sigmoid1» name: «sigmoid1» type: SIGMOID } В caffe реализована обертка на питоне, и следующий код инициализирует сеть и делает нормировку:
caffe.set_mode_gpu () net = caffe.Classifier ('deploy.prototxt', 'VGG_ILSVRC_19_layers.caffemodel', channel_swap=(2,1,0), raw_scale=255, image_dims=(options.width, options.height))
#…
out = net.forward_all (**{net.inputs[0]: caffe_in}) out = out['sigmoid1'].reshape (out['sigmoid1'].shape[0], np.prod (out['sigmoid1'].shape[1:])) out = (out — 0.5)/0.5 Итак, на данный момент у нас на руках есть бинарное (ну или почти) представление изображений векторами высокой размерности, в моем случае 4608, осталось обучить Deep Befief Network для сжатия этих представлений. Итоговая модель стала еще более глубокой сетью. Не дожидаясь, пока несколько дней будет обучаться DBN, давайте проведем эксперимент на поиск: будем выбирать случайное изображение и для него искать несколько ближайших, в смысле расстояния Хэмминга. Заметьте, это все на сырых фичах, на векторе высокой размерности, без всякого взвешивания признаков.
Пояснения: первая картинка — это картинка запрос, случайное изображение из базы; остальные — это ближайшие к ней.
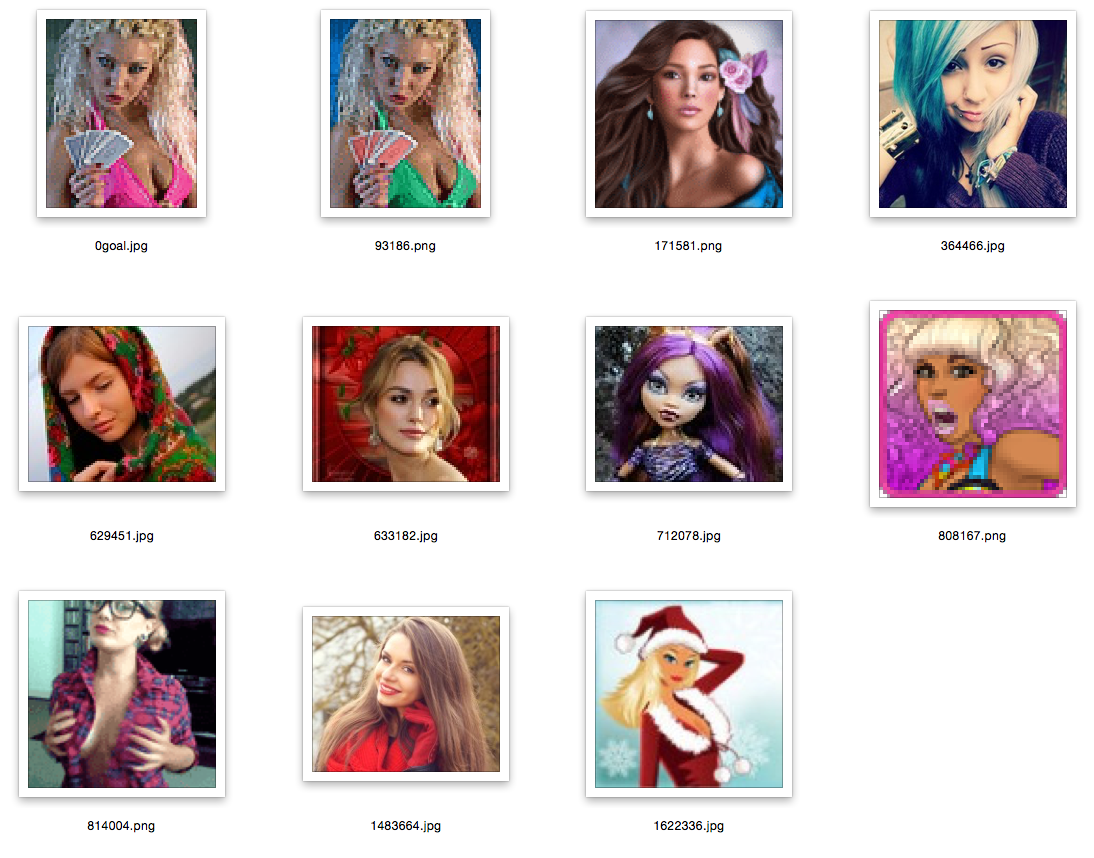
остальные примеры в спойлере
Я думаю, вы легко можете придумать пример, в котором не просто перенесете статические слои, но и натренируете их по-своему. Скажем, вы можете инициализировать часть своей сети, используя другую сеть, а затем дообучить на своих классах.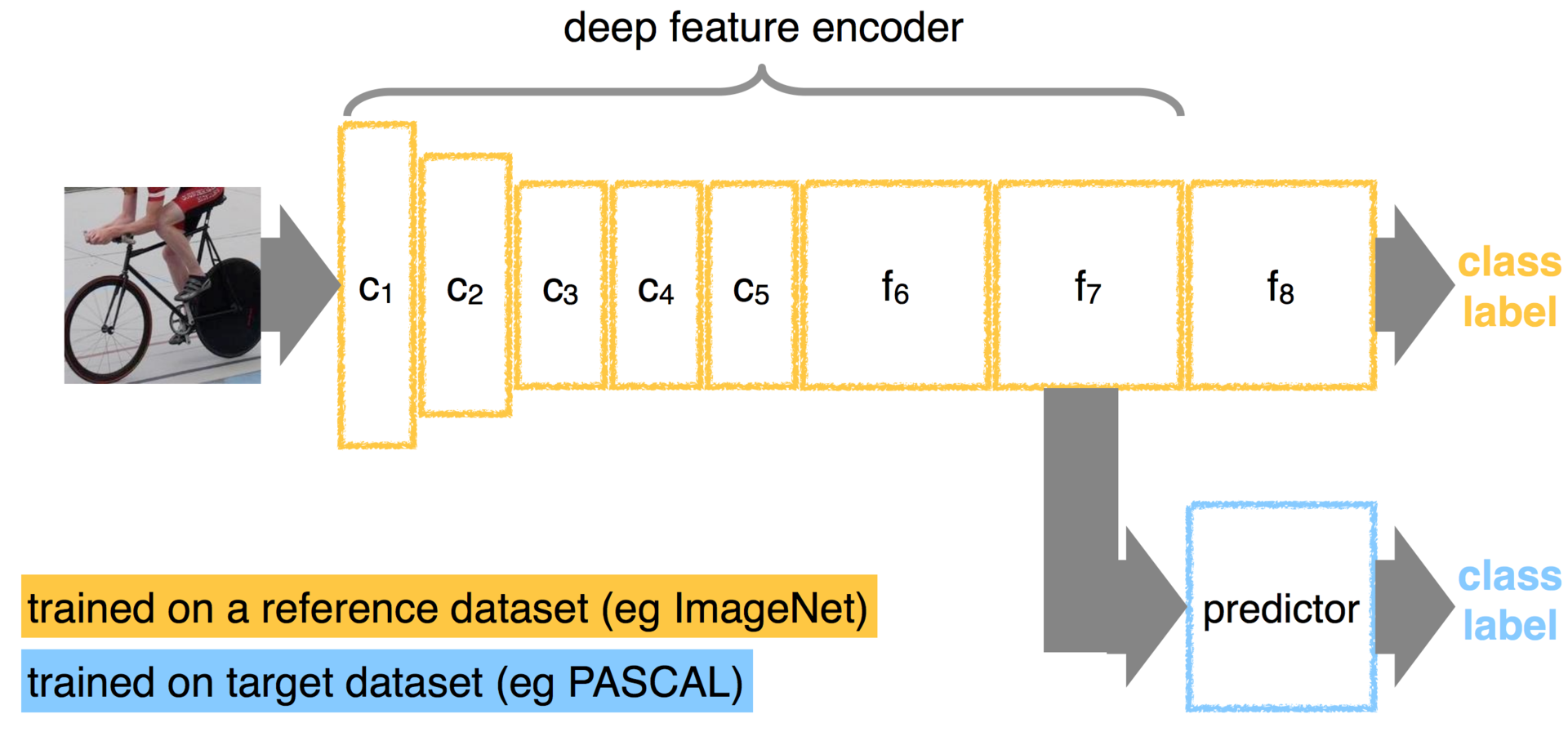
А если попробовать что-то более близкое к эксперименту, описанному в первой части? Пожалуйста: вот пример статьи, где используется convolutional deep belief networks для извлечения признаков из аудиосигналов. Почему бы не использовать обученные свертки для инициализации весов cDBN? Чем такая вот спектрограма не изображение, и почему бы низкоуровневым признакам не работать на ней:
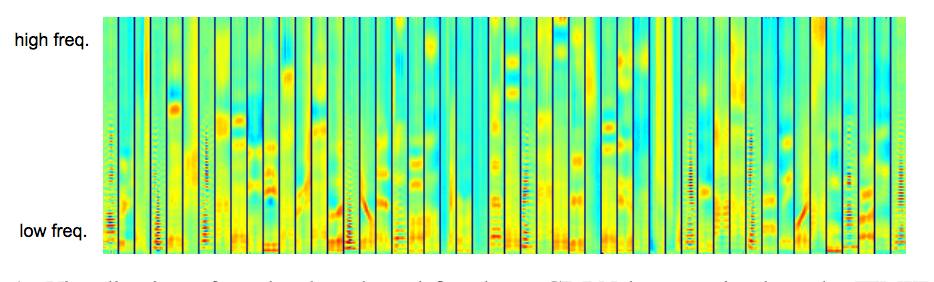
Если хотите поэкспериментировать с обработкой естественного языка и попробовать transfer learning, то вот подходящая статья ЛеКуна для старта. И да, там тоже текст представляется в виде изображения.
В общем, transfer learning — отличная штука, а caffe — крутая библиотека для глубокого обучения.
Ссылок много в тексте, приведу некоторые из них тут:
